Distance between two points
1.दो बिंदुओं के बीच की दूरी (Distance between two points),कोऑर्डिनेट जियोमेट्री में दो बिंदुओं के बीच की दूरी (Distance between two points in Coordinate Geometry)-
दो बिंदुओं के बीच की दूरी (Distance between two points),कोऑर्डिनेट जियोमेट्री में दो बिंदुओं के बीच की दूरी (Distance between two points in Coordinate Geometry) का अध्ययन वैश्लेषिक ज्यामिति में करते हैं।
इसमें बिन्दु की स्थिति, विशिष्ट संख्याओं जिन्हें निर्देशांक कहते हैं द्वारा निरूपित किया जाता है।वैश्लेषिक ज्यामिति में निर्देशांकों का प्रयोग होने के कारण इसे निर्देशांक ज्यामिति कहते हैं।
(1.)कार्तीय निर्देशांक (Cartesian Coordinate)-
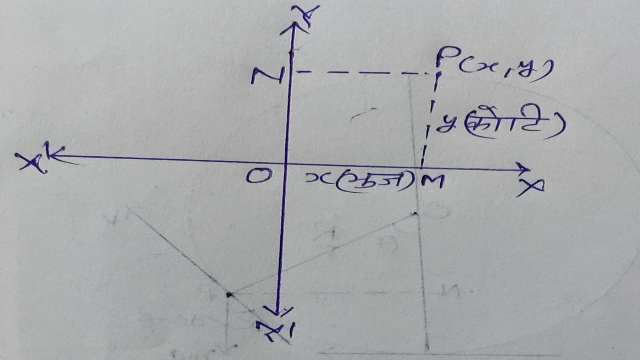
माना कि समतल में दो परस्पर लम्बवत् रेखाओं XOX’ और YOY’ है जो कि बिन्दु O पर प्रतिच्छेद करती हैं। इन्हें निर्देशांक अक्ष (Coordinate axes) कहते हैं और O को मूलबिन्दु (Origin) कहते हैं।XOX’ और YOY’ परस्पर लम्बवत् हैं, अतः XOX’ और YOY’ को समकोणिक अक्ष या आयतीय निर्देशांक अक्ष (rectangular axes) कहते हैं।
अब समतल में बिन्दु P के निर्देशांक ज्ञात करने के लिए बिन्दु P से XOX’ या x-अक्ष पर लम्ब PM और YOY’ या y-अक्ष पर लम्ब PN डालते हैं।मूलबिन्दु O से M की दिष्ट दूरी (OM=x) बिन्दु P का x-निर्देशांक या कोटि (Ordinate) कहलाती है।बिन्दु जिसका भुज x और कोटि y हो,बिन्दु (x,y) अर्थात् P(x,y) कहलाता है।बिन्दु के निर्देशांक लिखते समय x-निर्देशांक पहले और y-निर्देशांक बाद में लिखते हैं और उन्हें अल्पविराम (,) से अलग करते हुए छोटे कोष्ठक में लिखते हैं।
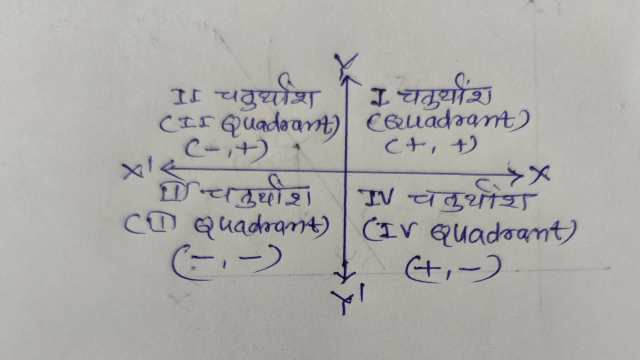
(2.)चतुर्थांश में निर्देशांकों के चिन्ह (Sign of Co-ordinate in Quardrants)-
चित्र में दोनों अक्ष XOX’ और YOY’ समतल को चार भागों में विभाजित करती है। इन्हें चतुर्थांश कहते हैं।XOY,YOX’,X’OY’ और Y’OX को क्रमशः प्रथम,द्वितीय,तृतीय और चतुर्थ चतुर्थांश कहते हैं।हम सदैव OX और OY दिशाओं को धनात्मक और OX’ व OY’ दिशाओं को ऋणात्मक लेते हैं।
यदि समतल में किसी बिन्दु के निर्देशांक (x,y) हो तो
प्रथम चतुर्थांश में x>0,y>0 ; निर्देशांक (+,+)
द्वितीय चतुर्थांश में x<0,y>0 ; निर्देशांक (-,+)
तृतीय चतुर्थांश में x<0,y<0 ; निर्देशांक (-,-)
चतुर्थ चतुर्थांश में x>0,y<0 ; निर्देशांक (+,-)
टिप्पणी:
(i)किसी बिन्दु P के निर्देशांक (x,y) हैं तो इसे P(x,y) लिखते हैं।
(ii) किसी बिन्दु का भुज,बिन्दु की y-अक्ष से लम्बवत् दूरी होती है।
(iii) किसी बिन्दु की कोटि, बिन्दु की x-अक्ष से लम्बवत् दूरी होती है।
(iv) किसी बिन्दु का भुज,y-अक्ष के दायीं ओर धनात्मक और बायीं ओर ऋणात्मक होता है।
(v) किसी बिन्दु की कोटि,x-अक्ष के ऊपर धनात्मक और नीचे ऋणात्मक होती है।
(vi) यदि y=0 हो तो बिन्दु x-अक्ष पर स्थित होता है।
(vii) यदि x=0 हो तो बिन्दु y-अक्ष पर स्थित होता है।
(viii) यदि x=0,y=0 हो तो बिन्दु मूलबिन्दु है।
(3.) दो बिंदुओं के बीच की दूरी (Distance between two points)-
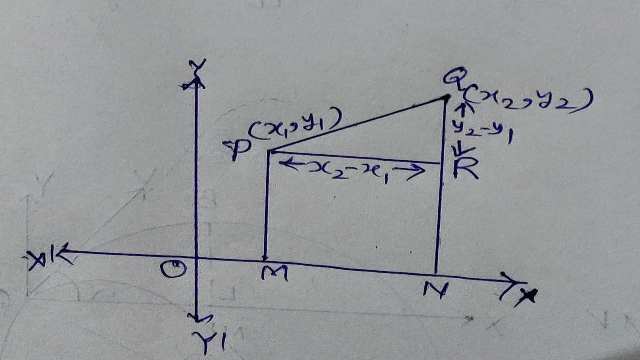
माना XOX’ और YOY’ निर्देशांक अक्ष हैं और समतल में स्थित दो बिन्दु P(x_{1},y_{1}) और Q(x_{2},y_{2}) है जिनके बीच की दूरी ज्ञात करनी है।बिन्दु P और Q से x-अक्ष पर लम्ब क्रमशः PM और QN डालते हैं और P से QN पर लम्ब PR डाला। अतः
OM=P का भुज=x_{1}
इसी प्रकार ON=x_{2},PM=y_{1} और QN=y_{2}
अतः चित्रानुसार
PR=MN=ON-OM=x_{2}-x_{1}
और
QR=QN-RN=QN-PM=y_{2}-y_{1}
अतः समकोण त्रिभुज PRQ में बौधायन सूत्र से-
P Q^{2}=P R^{2}+Q R^{2}
या P Q^{2}=\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2} \\ =\sqrt{\left(x_{2}-x_{1}\right)^{2}+ \left(y_{2}-y_{1}\right)^{2}} \\ =\sqrt{\left( \text {x-निर्देशांकों का अन्तर} \right)^{2}+ \left( \text { y-निर्देशांकों का अन्तर} \right)^{2}}
जो कि दो बिन्दुओं के बीच की दूरी का सूत्र है।
विशेष स्थिति:मूल बिन्दु O(0,0) से किसी बिन्दु P(x,y) की दूरी
O P=\sqrt{x^{2}+y^{2}}
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Trigonometric Ratios of Special Angles
2.दो बिंदुओं के बीच की दूरी के उदाहरण (Distance between two points Examples),कोऑर्डिनेट जियोमेट्री में दो बिंदुओं के बीच की दूरी के उदाहरण (Distance between two points in Coordinate Geometry Examples)-
Example-1.निम्नलिखित बिन्दुओं के मध्य दूरी ज्ञात कीजिए:
(i) (-1,-1) और (8,-2)
(ii) \left(a t_{1}^{2}, 2 a t_{1}\right) और \left(a t_{2}^{2}, 2 a t_{2}\right)
Solution– (i) (-1,-1) और (8,-2)
माना बिन्दु P(-1,-1) तथा Q(8,-2) हैं अतः P व Q के मध्य दूरी PQ है।
दूरी सूत्र-
PQ =\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ PQ=\sqrt{(8-(-1))^{2}+(-2-(-1))^{2}} \\ =\sqrt{(8+1)^{2}+(-2+1)^{2}} \\ =\sqrt{(9)^{2}+(-1)^{2}} \\ =\sqrt{81+1} \\ =\sqrt{82}
(ii) \left(a t_{1}^{2}, 2 a t_{1}\right) और \left(a t_{2}^{2}, 2 a t_{2}\right)
माना बिन्दु P\left(a t_{1}^{2}, 2 a t_{1}\right) तथा Q\left(a t_{2}^{2}, 2 a t_{2}\right) हैं। अतः P व Q के मध्य की दूरी PQ है।
दूरी सूत्र-
PQ =\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ =\sqrt{\left(a t_{2}^{2}-a t_{1}^{2}\right)^{2} +\left(2 a t_{2}-2a +1\right)^{2}} \\ =\sqrt{a^{2}\left(t_{2}^{2}-t_{1}^{2}\right)^{2}+4 a^{2}\left(t_{2}-t_{1}\right)^{2}} \\ =\sqrt{a^{2}\left\{\left(t_{2}-t_{1}\right)^{2}\left(t_{2}+ t_{1}\right)^{2} +4\left(t_{2}- t_{1}\right)^{2}\right \}} \\ =a \sqrt{\left(t_{2}-t_{1}\right)^{2}\left[\left(t_{2} +t_{1}\right)^{2}+4 \right]} \\ PQ =a\left(t_{2}-t_{1}\right) \sqrt{\left(t_{2}+t_{1}\right)^{2}+4}
Example-2. सिद्ध कीजिए कि बिन्दु (2,-2),(-2,1) और (5,2) एक समकोण त्रिभुज के शीर्ष हैं।
Solution– माना बिन्दु A(2,-2),B(-2,1) और (5,2) हैं।
अतः दूरी सूत्र- PQ=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ AB=\sqrt{(-2-2)^{2}+(1-(-2))^{2}}
\Rightarrow A B=\sqrt{(-4)^{2}+(1+2)^{2}} \\ \Rightarrow A B=\sqrt{16+9} \\ \Rightarrow A B=\sqrt{25} \\ \Rightarrow A B=5 \\ B C =\sqrt{(5-(-2))^{2}+(2-1)^{2}} \\ =\sqrt{(5+2)^{2}+(1)^{2}} \\ =\sqrt{49+1} \\ \Rightarrow B C=\sqrt{50} \\ A C=\sqrt{(5-2)^{2}+(2-(-2))^{2}} \\ \Rightarrow A C=\sqrt{(3)^{2}+(2+2)^{2}} \\ =\sqrt{9+16} \\ =\sqrt{25} \\ \Rightarrow A C=5 \\ A B^{2}+A C^{2} =5^{2}+5^{2} \\ =25+25 \\ =50 \\ \Rightarrow A B^{2}+A C^{2}=B C^{2}
अतः पाइथागोरस प्रमेय से बिन्दु समकोण त्रिभुज के शीर्ष हैं।
Example-3. सिद्ध कीजिए कि बिन्दु (1,-2),(3,0),(1,2) और (-1,0) एक वर्ग के शीर्ष हैं।
Solution-माना बिन्दु A(1,-2),B(3,0),C(1,2) और (-1,0) हैं।
अतः दूरी सूत्र से
PQ=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ A B =\sqrt{(3-1)^{2}+(0-(-2))^{2}} \\ =\sqrt{(2)^{2}+(2)^{2}} \\ = \sqrt{4+4} \\ =\sqrt{8} \\ AB=2 \sqrt{2} unit \\ B C =\sqrt{(1-3)^{2}+(2-0)^{2}} \\ =\sqrt{(-2)^{2}+(2)^{2}} \\ =\sqrt{4+4} \\ =\sqrt{8} \\ \Rightarrow B C=2 \sqrt{2} \text { } \\ C D =\sqrt{(-1-1)^{2}+(0-2)^{2}} \\ =\sqrt{(-2)^{2}+(-2)^{2}} \\ =\sqrt{4+4} \\ =\sqrt{8} \\ \Rightarrow CD =2 \sqrt{2} \text { unit } \\ D A=\sqrt{(-1-1)^{2}+(0-(-2))^{2}} \\ =\sqrt{(-2)^{2}+(2)^{2}} \\ =\sqrt{4+4} \\ DA =\sqrt{8} \\ DA=2 \sqrt{2} \text { unit } \\ \Rightarrow AC =\sqrt{(1-1)^{2}+(2-(-2))^{2}} \\ A C =\sqrt{0^{2}+(2+2)^{2}} \\ =\sqrt{0^{2}+(2+2)^{2}} \\ =\sqrt{4^{2}} \\ \Rightarrow A C=4 \text { unit } \\ B D=\sqrt{(-1-3)^{2}+(\theta-0)^{2}} \\=\sqrt{(-4)^{2}+0^{2}} \\ =\sqrt{16} \\ \Rightarrow B D=4 \text { unit }
अतः भुजा AB=भुजा BC=भुजा CD=भुजा DA
तथा विकर्ण AC=विकर्ण BD
अतः एक ABCD वर्ग है।
Example-4. सिद्ध कीजिए कि बिन्दु (a,a),(-a,-a) और (-\sqrt{3} a,\sqrt{3} a) एक समबाहु त्रिभुज के शीर्ष हैं।
Solution– माना बिन्दु A(a,a),B(-a,-a) और (-\sqrt{3} a,\sqrt{3} a) हैं।
अतः दूरी सूत्र से –\Rightarrow P Q=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ A B=\sqrt{(-a-a)^{2}+(-a-a)^{2}} \\ \Rightarrow A B=\sqrt{(-2 a)^{2}+(-2 a)^{2}} \\ =\sqrt{4 a^{2}+4 a^{2}} \\ =\sqrt{8 a^{2}} \\ A B =2 \sqrt{2} a \text { unit } \\ B C =\sqrt{(-\sqrt{3} a-(-a))^{2}+(-\sqrt{3} a-(-a))^{2}} \\ =\sqrt{(-\sqrt{3} a+a)^{2}+(-\sqrt{3} a+a)^{2}} \\=\sqrt{3 a^{2}+a^{2}-2 \sqrt{3} a^{2}+3 a^{2}+a^{2}-2 \sqrt{3} a^{2}} \\ =\sqrt{8 a^{2}} \\ \Rightarrow B C=2 \sqrt{2} a \text { unit } \\ AC =\sqrt{(-\sqrt{3} a-a)^{2}+(\sqrt{3} a-a)^{2}} \\=\sqrt{3 a^{2}+a^{2}+2 \sqrt{3} a^{2}+3 a^{2}+a^{2}-2 \sqrt{3} a^{2}} \\ =\sqrt{8 a^{2}} \\ \Rightarrow A C=2 \sqrt{2} a \text { unit }
अतः AB=BC=CA=2 \sqrt{2} a
फलत: समबाहु त्रिभुज है।
Example-5. सिद्ध कीजिए कि बिन्दु (1,1),(-2,7) और (3,-3) संरेख हैं।
Solution– माना बिन्दु A(1,1),B(-2,7) और C(3,-3) हैं।
दूरी सूत्र-
PQ=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ A B=\sqrt{(-2-1)^{2}+(7-1)^{2}} \\=\sqrt{(-3)^{2} +(6)^{2}} \\ =\sqrt{9+36} \\ =\sqrt{45} \\ \Rightarrow A B =3 \sqrt{5} \text { unit } \\BC=\sqrt{(3-(-2))^{2}+(-37)^{2}} \\ =\sqrt{(3+2)^{2}+(-10)^{2}} \\ =\sqrt{(5)^{2}+100} \\ =\sqrt{25+100} \\ =\sqrt{125} \\ \Rightarrow B C =5 \sqrt{5} \text { unit } \\ A C=\sqrt{(3-1)^{2}+(-3-1)^{2}} \\ =\sqrt{2^{2}+(-4)^{2}} \\ =\sqrt{4+16} \\ =\sqrt{20} \\ \Rightarrow A C=2 \sqrt{5} \text { unit } \\ A B+A C=3 \sqrt{5}+2 \sqrt{5} \\ =5 \sqrt{5} \\ \Rightarrow A B+A C=B C
अतः बिन्दु A,B,C संरेख हैं।
Example-6.x-अक्ष पर वह बिन्दु ज्ञात कीजिए जो बिन्दुओं (-2,-5) और (2,-3) से समान दूरी पर स्थित है
Solution- माना बिन्दु A(-2,-5)व B(2,-3) हैं।तथा इनसे समान दूरी पर x-अक्ष पर स्थित बिन्दु P(x,0) है।
दूरी सूत्र-
PQ =\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ P A =\sqrt{(x-(-2))^{2}+(0-(-5))^{2}} \\ =\sqrt{(x+2)^{2}+25} \\ =\sqrt{x^{2}+4 x+4+25} \\ =\sqrt{x^{2}+4 x+29} \\ PB =\sqrt{(x-2)^{2}+(0-(-3))^{2}} \\ P B =\sqrt{x^{2}-4 x+4+9} \\ =\sqrt{x^{2}-4 x+13}
प्रश्नानुसार- PA=PB
\sqrt{x^{2}+4 x+29}=\sqrt{x^{2}-4 x+13} \\ \Rightarrow x^{2}+4 x+29=x^{2}-4 x+13 \\ \Rightarrow 4 x+4 x=13-29 \\ \Rightarrow 8 x=-16 \\ \Rightarrow x = \frac{-16}{8} \\ \Rightarrow x=-2
अतः बिन्दु P(-2,0) है।
Example-7. y-अक्ष पर वह बिन्दु ज्ञात कीजिए जो बिन्दुओं (-5,-2) और (3,2) से समान दूरी पर स्थित है।
Solution– माना बिन्दु A(-5,-2) व B(3,2) हैं। इनसे y-अक्ष पर समान दूरी पर स्थित बिन्दु P(0,y) है।
दूरी सूत्र-
\Rightarrow PQ =\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ PA =\sqrt{(0-(-5))^{2}+(y-(-2)]^{2}} \\ =\sqrt{25+(y+2)^{2}} \\ =\sqrt{25+y^{2}+4 y+4} \\ PA =\sqrt{y^{2}+4 y+29} \\ PB =\sqrt{(0-3)^{2}+(y-2)^{2}} \\ =\sqrt{9+y^{2}-4 y+4} \\ \Rightarrow PB=\sqrt{y^{2}-4 y+13}
प्रश्नानुसार PA=PB
\sqrt{y^{2}+4 y+29}=\sqrt{y^{2}-4 y+13} \\ \Rightarrow y^{2}+4 y+29=y^{2}-4y+13 \\ \Rightarrow 8 y=13-29 \\ \Rightarrow 8 y=-16 \\ \Rightarrow y=-2
अतः बिन्दु P(0,-2) होगा।
Example-8. यदि P और Q के निर्देशांक क्रमशः (a \cos \theta, b \sin \theta) और (-a \sin \theta, b \cos \theta) हैं तो सिद्ध कीजिए कि जहां O मूलबिन्दु है।
Solution–P(a \cos \theta, b \sin \theta), Q(-a \sin \theta, b \cos \theta) तथा O(0,0)
दूरी सूत्र-
P Q=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left( y_{2}-y_{1}\right)^{2}} \\ OP=\sqrt{(a \cos \theta-0)^{2}+(b \sin n-0)^{2}} \\ OP^{2}=a^{2} \cos ^{2} \theta+b^{2} \sin ^{2} \theta \\ OQ=\sqrt{(-a \sin \theta-0)^{2}+(b \cos \theta-0)^{2}} \\ OQ^{2}=a^{2} \sin ^{2} \theta+b^{2} \cos ^{2} \theta \\ \Rightarrow O P^{2}+OQ^{2}=a^{2} \sin ^{2} \theta+b^{2} \cos ^{2} \theta+a^{2} \cos ^{2} + b^{2} \sin ^{2} \theta \\ =a^{2}\left(\sin ^{2} \theta+\cos ^{2} \theta\right)+ b^{2}\left(\cos ^{2} \theta+\sin ^{2} \theta\right) \\ \Rightarrow OP^{2}+ OQ^{2}=a^{2}+b^{2}
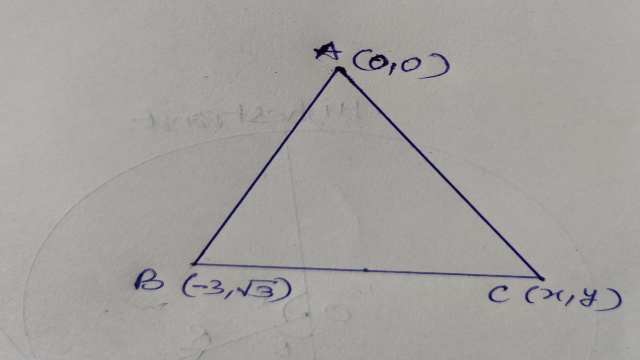
Example-9.यदि एक समबाहु त्रिभुज के दो शीर्ष (0,0) व (-3,-3\sqrt{3}) हों तो तीसरा शीर्ष ज्ञात करो।
Solution– माना बिन्दु A(0,0), B(-3,-3\sqrt{3}) तथा C(x,y,) हैं।
समबाहु त्रिभुज के लिए AB=BC=CA
\Rightarrow A B^{2}=B C^{2}=C A^{2}
दूरी सूत्र-
P Q =\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ P Q^{2} =\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2} \\ A B^{2} =(-3-0)^{2}+(\sqrt{3}-0)^{2} \\ =9+3 \\ \Rightarrow A B^{2} =12 ....(1) \\ \Rightarrow A B^{2}=12-\cdots(1) \\ B C^{2}=(x+3)^{2}+(y-\sqrt{3})^{2} \\ =x^{2}+6 x+9+y^{2}-2 \sqrt{3} y+3 \\ BC^{2}=x^{2}+6 x+y^{2}-2 \sqrt{3} y+12 \\ AC^{2}=(x-0)^{2}+(y-0)^{2} \\ \Rightarrow A C^{2}=x^{2}+y^{2}....(3)
समीकरण (1) व (3) से-
x^{2}+y^{2}=12 \quad\left[\because A B^{2}=BC^{2}\right]...(4)
समीकरण (2) व (3) से-
x^{2}+6 x+y^{2}-2 \sqrt{3} y+12=12 \quad\left[\because A B^{2}=BC^{2}\right] \\ \Rightarrow 12+6 x-2 \sqrt{3} y+12=12 \\ \Rightarrow \quad 6 x-2 \sqrt{3} y=-12 \\ \Rightarrow 2 \sqrt{3}(\sqrt{3} x-y)=-12 \\ \Rightarrow \sqrt{3} x-y=-2 \sqrt{3} \\ \Rightarrow y=\sqrt{3} x+2 \sqrt{3}...(5)
समीकरण (4) में (5) से मान रखने पर-
x^{2}+\left(\sqrt{3} x+2 \sqrt{3} \right)^{2}=12 \\ \Rightarrow x^{2}+3 x^{2}+12+12 x=12 \\ \Rightarrow 4x^{2}+2 x=0 \\ \Rightarrow x(4 x+12)=0 \\ \Rightarrow 4x+12=0, x=0 \\ \Rightarrow x=-\frac{12}{4} \\ \Rightarrow x=-3
x का मान समीकरण (5) में रखने पर-
y=\sqrt{3}(-3)+2 \sqrt{3} \\ \Rightarrow y=-\sqrt{3}
जब x=0 तो
y=\sqrt{3}(0)+2 \sqrt{3} \\ y=2 \sqrt{3}
अतः C के निर्देशांक (-3,-3\sqrt{3}) या (0,2\sqrt{3})होंगे।
उपर्युक्त उदाहरणों के द्वारा दो बिंदुओं के बीच की दूरी (Distance between two points),कोऑर्डिनेट जियोमेट्री में दो बिंदुओं के बीच की दूरी (Distance between two points in Coordinate Geometry) को समझा जा सकता है।
3.दो बिंदुओं के बीच की दूरी की समस्याएं (Distance between two points Problems),कोऑर्डिनेट जियोमेट्री में दो बिंदुओं के बीच की दूरी की समस्याएं (Distance between two points in Coordinate Geometry Problems)-
(1.) बिन्दुओं (-6,7) और (-1,-5) के बीच दूरी ज्ञात करो।
(2.)यदि बिन्दुओं (3,k) और (k,5) से बिन्दु (0,2) की दूरी दूरियां बराबर हो तो k का मान ज्ञात कीजिए।
(3.) यदि बिन्दु (x,3) और (5,7) के बीच दूरी 5 हो तो x का मान ज्ञात कीजिए।
(4.) सिद्ध कीजिए कि बिन्दु (-2,-1),(-1,1),(5,2) और (4,-4) एक आयत के शीर्ष हैं।
(5.) यदि बिन्दु (x,y) बिन्दुओं (a+b,b-a) और (a-b,a+b) से बराबर दूरी पर हो तो सिद्ध कीजिए bx=ay.
(6.) किसी समतल में चार बिन्दु P(2,-1),Q(3,4),R(-2,3) और S(-3,-2) हैं तो सिद्ध कीजिए कि PQRS वर्ग नहीं एक समचतुर्भुज है।
(7.) सिद्ध कीजिए कि समकोण त्रिभुज AOB में कर्ण का मध्य बिन्दु C त्रिभुज के शीर्षों O,A और B से बराबर दूरी पर स्थित है।
(8.) उस त्रिभुज की माध्यिकाओं की लम्बाईयां ज्ञात कीजिए जिसके शीर्ष (1,-1),(0,4) और (-5,3) हैं।
उत्तर (Answer)-
(1.)13
(2.)k=1
(3.)x=2,8
(8) \frac{\sqrt{130}}{2},\frac{\sqrt{130}}{2}, \sqrt{13}
उपर्युक्त सवालों को हल करने पर दो बिंदुओं के बीच की दूरी (Distance between two points),कोऑर्डिनेट जियोमेट्री में दो बिंदुओं के बीच की दूरी (Distance between two points in Coordinate Geometry) को ठीक से समझ सकते हैं।
4.दो बिंदुओं के बीच की दूरी के लिए सूत्र क्या है? (What is the formula for distance between two points?),आप ज्यामिति में दूरी कैसे ज्ञात करते हैं? (How do you find distance in geometry?),दो बिंदुओं के बीच की दूरी सूत्र (Distance between two points formula), दो बिंदुओं के बीच की दूरी ज्ञात कीजिए (Find the distance between two points)-
दूरी सूत्र का उपयोग करके दो बिंदुओं के बीच की दूरी का पता लगाना सीखें, जो कि पाइथागोरस प्रमेय का एक अनुप्रयोग है।हम पाइथागोरस प्रमेय को किसी भी दो बिंदुओं के बीच की दूरी का पता लगाने के लिए PQ =\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} के रूप में लिख सकते हैं।
5.आप निर्देशांक के बीच की दूरी को कैसे पाते हैं? (How do you find the distance between coordinates?),दूरी सूत्र (Distance formula)-
जब हम दो बिंदुओं के बीच क्षैतिज और ऊर्ध्वाधर दूरी जानते हैं तो हम इस तरह से सीधी रेखा की दूरी की गणना कर सकते हैं: दूरी = \sqrt{\left(a\right)^{2}+\left(b\right)^{2}}
उपर्युक्त प्रश्नों के उत्तर द्वारा दो बिंदुओं के बीच की दूरी (Distance between two points),कोऑर्डिनेट जियोमेट्री में दो बिंदुओं के बीच की दूरी (Distance between two points in Coordinate Geometry) को ओर ठीक से समझ सकते हैं।
Also Read This Article:-Trigonometric Identities Formula
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |