Surface Area and Volume of Cone
1.शंकु का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cone):
शंकु का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cone):लंब वृत्तीय शंकु वह ठोस आकृति है जब कोई रेखाखंड एक स्थिर बिंदु पर एक स्थिर रेखा से अचर कोण पर परिक्रमा करती है।
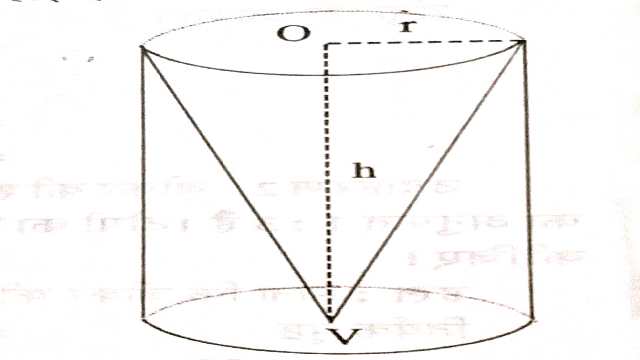
चित्र में V एक स्थिर बिन्दु तथा रेखा VA परिक्रमा रेखा है।जो VO के साथ कोण (माना) बनाती है।स्थिर बिंदु V को शीर्ष,रेखा VA को शंकु का जनक तथा स्थिर रेखा VO को अक्ष कहते हैं।शंकु का आधार एक वृत्त होता है।वृत्त के केंद्र और शंकु के शीर्ष को मिलाने वाली रेखा शंकु का अक्ष कहलाती है।लंबवृत्तीय शंकु का अक्ष आधार पर लंबवत होता है।
अतः हम कह सकते हैं कि जब केवल रेखाखंड को अक्ष VO के सापेक्ष परिक्रमा कराते हैं तो खोखला शंकु प्राप्त होता है जिसका आधार खुला होता है।यदि रेखाखंड VA और त्रिज्या OA को अक्ष OA के सापेक्ष परिक्रमण कराते हैं तो बंद आधार वाला खोखला शंकु जनित होता है और यदि त्रिभुज VIA के क्षेत्र को अक्ष VO के सापेक्ष परिक्रमण कराते हैं तो ठोस शंकु प्राप्त होता है।रेखाखंड VO और VA को क्रमशः शंकु की ऊँचाई और तिर्यक (तिरछी) ऊंचाई कहते हैं जिन्हें प्रायः h और l से प्रदर्शित करते हैं तथा वृत्तीय आधार की त्रिज्या शंकु की त्रिज्या कहलाती है।जिसे r से व्यक्त करते हैं।अतः चित्र से
V A^{2}=VO^{2}+OA^{2} \\ \Rightarrow l^{2}=h^{2}+r^{2} \\ \Rightarrow l=\sqrt{h^{2}+r^{2}}
जो कि शंकु की त्रिज्या, ऊँचाई और तिर्यक ऊँचाई में सम्बन्ध हैं।यदि हम एक त्रिज्यखंड VAB लें तथा उसकी सीधी कोरों VA और VB को संपाती कर दें तो शंकु जनित होगा।जिसके आधार का परिमाप चाप AB की लंबाई के बराबर तथा त्रिज्यखंड की त्रिज्या शंकु की तिर्यक ऊंचाई l होगी।
शंकु का वक्र पृष्ठीय क्षेत्रफल=त्रिज्यखण्ड VAB का क्षेत्रफल
=\frac{1}{2} \times \text{ त्रिज्यखण्ड के चाप की लम्बाई } \times \text{ त्रिज्यखण्ड की त्रिज्या } \\ =\frac{1}{2} \times \text{ शंकु के आधार का परिमाप } \times \text{ तिर्यक ऊँचाई } \\ =\frac{1}{2} \times 2 \pi r \times l=\pi r l
अतः शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल=शंकु का वक्र पृष्ठीय क्षेत्रफल + आधार का क्षेत्रफल
\pi r l+\pi r^{2} \\ =\pi(l+r) r
तथा शंकु का आयतन=\frac{1}{3} \pi r^{2} h
शंकु का आयतन=\frac{1}{3} बेलन का आयतन
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Surface Area and Volume of Cylinder
2.शंकु का पृष्ठीय क्षेत्रफल और आयतन के उदाहरण (Surface Area and Volume of Cone Examples):
Example:1.एक शंकु की ऊँचाई 28 सेमी तथा आधार की त्रिज्या 21 सेमी है।उसका वक्र पृष्ठीय क्षेत्रफल, सम्पूर्ण पृष्ठीय क्षेत्रफल तथा आयतन ज्ञात कीजिए।
Solution:h=28 सेमी,r=21 सेमी
l^{2} =r^{2}+h^{2} \\ =(21)^{2}+(28)^{2} \\ =441+784 \\ \Rightarrow l^{2} =1225 \\ \Rightarrow l =\sqrt{1225} \\ l=35 सेमी
शंकु का वक्र पृष्ठीय क्षेत्रफल=\pi r l \\ =\frac{22}{7} \times 21 \times 35 \\ =2310 \text { वर्ग सेमी }
शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल=\pi r\left ( r+l \right ) \\ =\frac{22}{7} \times 21 \times(21+35) \\ =3696 \text { वर्ग सेमी }
शंकु का आयतन=\frac{1}{3} \pi r^{2} h \\ =\frac{1}{3} \times \frac{22}{7} \times(21)^{2} \times 28 \\ =\frac{1}{3} \times \frac{22}{7} \times 21 \times 21 \times 28 \\= 12,936 \text { घन सेमी }
Example:2.एक लम्बवृत्तीय शंकु का आयतन 1232 घन सेमी है तथा उसकी ऊँचाई 24 सेमी है तो शंकु की तिरछी ऊँचाई ज्ञात कीजिए।
Solution:शंकु की ऊँचाई (h)=24 सेमी
शंकु का आयतन=\frac{1}{3} \pi r^{2} h \\ =\frac{1}{3} \times \frac{22}{7} \times r^{2} \times 24=1232 \\ r^{2}=\frac{1232 \times 3 \times 7}{22 \times 24} \\ r^{2}=49 \\ \Rightarrow r =\sqrt{49} \\ \Rightarrow r=7 \text { सेमी }
शंकु की तिरछी ऊँचाई l=\sqrt{r^{2}+h^{2}} \\ l=\sqrt{(7)^{2}+(24)^{2}}\\ \Rightarrow l=\sqrt{49+576}\\ l=\sqrt{625}\\ l=25 \text { सेमी }
Example:3.एक शंकु के आधार का व्यास 14 मीटर और तिर्यक ऊँचाई 25 मीटर है तो शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
Solution:आधार का व्यास=14 मीटर
त्रिज्या (r)=\frac{14}{2}=7 मीटर
तिर्यक ऊँचाई (l)=l^{2}=r^{2}+n^{2} \\ (25)^{2}=(7)^{2}+h^{2} \\ h^{2}=625-49 \\ \Rightarrow h=\sqrt{576} \\ h=24 \text { मीटर }
शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल=\pi r\left ( r+l \right ) \\ =\frac{22}{7} \times 7 \times(7+25) \\ =704 \text { वर्ग मीटर }
Example:4.शंकु के आधार की त्रिज्या 14 मीटर और तिरछी ऊँचाई 50 सेमी है।शंकु का पृष्ठीय क्षेत्रफल (वक्र पृष्ठीय क्षेत्रफल),सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
Solution:शंकु की त्रिज्या (r)=14 सेमी
तिरछी ऊँचाई (l)=50 सेमी
शंकु का वक्र पृष्ठीय क्षेत्रफल=\pi r l \\ =\frac{22}{7} \times 14 \times 50 \\ =2200 \text { वर्ग सेमी }
शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल=\pi r\left ( r+l \right ) \\=\frac{22}{7} \times 14 \times (14+50) \\ =\frac{22 }{7} \times 14 \times 64 \\ =2816 \text { वर्ग सेमी }
Example:5.लम्बवृत्तीय शंकु की ऊँचाई 8 सेमी और आधार की त्रिज्या 6 सेमी है।इसका आयतन ज्ञात कीजिए।
Solution:h=8 सेमी,r=6 सेमी
शंकु का आयतन=\frac{1}{3} \pi r^{2} h \\ =\frac{1}{3} \times \frac{22}{7} \times(6)^{2} \times 8 \\ =\frac{1}{3} \times \frac{22}{7} \times 36 \times 8 \\ =301.71 \text { घन सेमी }
Example:6.एक शंकु का वक्र पृष्ठीय क्षेत्रफल 1884.4 वर्गमीटर है तथा इसकी तिर्यक ऊँचाई 12 मीटर है।इसके आधार की त्रिज्या ज्ञात कीजिए।
Solution:तिर्यक ऊँचाई (l)=12 मीटर
वक्र पृष्ठीय क्षेत्रफल=1884.4 वर्गमीटर
\pi \times r \times l=1884.4 \\ \frac{22}{7} \times r \times 12=1884.4 \\ r=\frac{1884.4 \times 7}{22 \times 12} \\ =49.965 \times 100 \\ r =4996.50 \text { सेमी }
Example:7 लम्बवृत्तीय शंकु के आधार का क्षेत्रफल 154 वर्गसेमी है । इसकी तिरछी ऊँचाई 25 सेमी होती है तो शंकु की ऊँचाई ज्ञात कीजिए
Solution:-तिर्यक ऊँचाई(l)=25
शंकु के आधार का क्षेत्रफल=154 वर्गसेमी
\pi r^{2}=154 \\ \Rightarrow r^{2}=154 \times \frac{7}{22} \\ \Rightarrow r^{2}=49\\ \Rightarrow r=\sqrt{49} \\ r=7 \text{ सेमी } \\ l^{2}=r^{2}+h^{2} \\ (25)^{2}=(7)^{2}+h^{2} \\ \Rightarrow h^{2}=625-49 \\ \Rightarrow h=\sqrt{576}=24 \text{ सेमी }
Example:8.दो शंकुओं के आधार का व्यास समान है।उनकी तिरछी ऊँचाइयों का अनुपात 5:4 है।यदि छोटे शंकु का पृष्ठीय क्षेत्रफल 400 वर्गसेमी है तो बड़े शंकु का वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
Solution:आधार का व्यास समान हैं अतः दोनों शंकुओं की त्रिज्याएं समान होगी।अतः त्रिज्याएं=r
माना बड़े शंकु की तिर्यक ऊँचाई=l_{1}
छोटे शंकु की तिर्यक ऊँचाई=l_{2}
अत: l_{1}=5x,l_{2}=4x
छोटे शंकु का वक्र पृष्ठीय क्षेत्रफल=\pi r l_{2} \\ \pi r l_{2}=400
बड़े शंकु का वक्र पृष्ठीय क्षेत्रफल=\pi r l_{1}
अतः \frac{ \text{ बड़े शंकु का वक्र पृष्ठीय क्षेत्रफल }}{ \text{ छोटे शंकु का वक्र पृष्ठीय क्षेत्रफल } }=\frac{ \pi r l_{1} }{ \pi r l_{2} } \\ \frac{ \text{ बड़े शंकु का वक्र पृष्ठीय क्षेत्रफल } }{ 400 }=\frac{ \pi r \times 5x }{ \pi r \times 4x } \\ \Rightarrow \text{ बड़े शंकु का वक्र पृष्ठीय क्षेत्रफल }=\frac{5}{4} \times 500 =500 \text { वर्ग सेमी }
Example:9.एक शंकु की तिर्यक ऊँचाई और त्रिज्या का अनुपात 7:4 है।यदि इसके वक्र पृष्ठ का क्षेत्रफल 792 वर्गसेमी हो तो इसकी त्रिज्या ज्ञात कीजिए।
Solution:माना विमा =x
तिर्यक ऊँचाई (l)=7x
त्रिज्या (r)=4x
शंकु का वक्र पृष्ठ का क्षेत्रफल=\pi r l \\ \pi r l=792 \\ \pi r l=792 \\ \Rightarrow \frac{22}{7} \times 4 x \times 7 x=792 \\ \Rightarrow x^{2}=\frac{792}{22 \times 4} \\ \Rightarrow x^{2}=9 \\ \Rightarrow x=\sqrt{9}=3
अतः शंकु की त्रिज्या=4x=4 × 3=12 सेमी
Example:10.9 मीटर ऊँचे शंकु के आकार के टेंट के आधार की परिधि 44 मीटर है।इसके अन्दर की वायु का आयतन ज्ञात कीजिए।
Solution:माना आधार की त्रिज्या=r
h=9 मीटर
आधार की परिधि (वृत्त)=2 \pi r \\ 2 \pi r=44 \\ 2 \times \frac{22}{7} \times r=44 \\ \Rightarrow r=\frac{44 \times 7}{2 \times 22} \\ \Rightarrow r=7 \text{ मीटर }
अन्दर की वायु का आयतन=\frac{1}{3} \pi r^{2} h \\ =\frac{1}{3} \times \frac{22}{7} \times(7)^{2} \times 9 \\ =\frac{1}{3} \times \frac{22}{7} \times 7 \times 7 \times 49 \\ =22 \times 7 \times 3 \\ =462 \text{ घन मीटर }
Example:11.एक शंकु के आकार के बर्तन की त्रिज्या 10 सेमी और ऊँचाई 18 सेमी है।यह पानी से पूरा भराव हुआ है।इसे 5 सेमी त्रिज्या के बेलनाकार बर्तन में उँडेला जाता है।बेलनाकार बर्तन में पानी के तल की ऊँचाई ज्ञात कीजिए।
Solution:माना बेलन में x सेमी ऊँचाई तक पानी आता है।
अत: शंकु में पानी का आयतन=बेलन में पानी का आयतन
\frac{1}{3} \pi r^{2} h=\pi R^{2} x \\ \frac{1}{3} \times \pi \times(10)^{2} \times 18=\pi \times(5)^{2} \times x \\ \Rightarrow x=\frac{10 \times 10 \times 18}{3 \times 5 \times 5} \\ x=24 \text { सेमी }
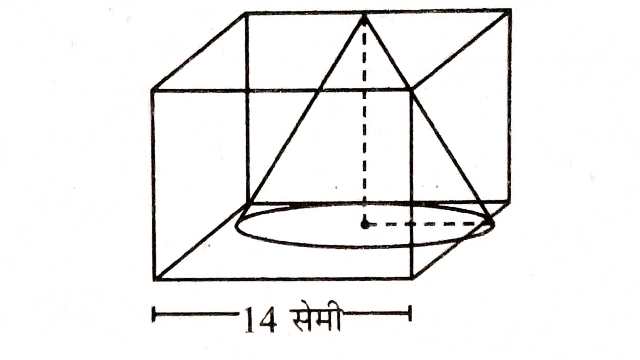
Example:12.14 सेमी भुजा के एक घन से बड़े से बड़ा शंकु काटा जाता है, शंकु का आयतन ज्ञात कीजिए।
Solution:घन की भुजा=14 सेमी
शंकु की त्रिज्या (r)=\frac{ 14}{ 2}=7 सेमी
शंकु की ऊँचाई (h)=14 सेमी
शंकु का आयतन=\frac{1}{3} \pi r^{2} h \\ =\frac{1}{3} \times \frac{22}{7} \times(7)^{2} \times 14 \\ =\frac{1}{3} \times \frac{22}{7} \times 7 \times 7 \times 14 \\ =718.666 \text { घन सेमी } \\ =718.67 \text { घन सेमी }
Example:13.शंकु के आधार की त्रिज्या और ऊँचाई क्रमशः 7 सेमी और 24 सेमी है।शंकु की तिरछी ऊँचाई, वक्र पृष्ठ का क्षेत्रफल,सम्पूर्ण पृष्ठीय क्षेत्रफल एवं आयतन ज्ञात कीजिए।
Solution:r=7 सेमी,h=24 सेमी
शंकु की तिर्यक (तिरछी) ऊँचाई=l
l^{2} = r^{2}+h^{2} \\ \Rightarrow l^{2} =(7)^{2}+(24)^{2} \\ =49+576 \\ =625 \\ \Rightarrow l =\sqrt{625} \\ \Rightarrow l=25 \text { सेमी }
शंकु का वक्र पृष्ठ का क्षेत्रफल=\pi r l \\ =\frac{22}{7} \times 7 \times 25=550 \text { वर्ग सेमी }
शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल=\pi r\left ( r+l \right ) \\ =22 \times 7 \times(7+25) \\ =22 \times 32=704 \text { वर्ग सेमी }
शंकु का आयतन=\frac{1}{3} \pi r^{2} h \\ =\frac{1}{3} \times \frac{22}{7} \times(7)^{2} \times 24 \\ =\frac{1}{3} \times \frac{22}{7} \times 7 \times 7 \times 24=1232 \text { घन सेमी }
Example:14.एक त्रिज्यखण्ड की त्रिज्या 12 सेमी और कोण 120° है।इसकी सीधी कोरों को सम्पाती करके एक शंकु बनाया जाता है।शंकु का आयतन ज्ञात कीजिए।
Solution:R=12 सेमी \quad \theta=120
बनाए गए शंकु का वक्र पृष्ठ का क्षेत्रफल=त्रिज्य खण्ड का क्षेत्रफल
\pi r l=\frac{\pi R^{2} \times \theta}{360} \\ \Rightarrow \pi \times r \times 12=\pi \times(12)^{2} \times \frac{120}{360} \\ \Rightarrow r=\frac{\pi \times 12 \times 12 \times 120}{12 \times \pi \times 360} \\ \Rightarrow r=4 \text { सेमी }
शंकु की तिर्यक ऊँचाई (l)=12 सेमी
त्रिज्या (r)=4 सेमी
l^{2}=r^{2}+h^{2} \\ (12)^{2}=(4)^{2}+h^{2} \\ \Rightarrow h^{2}=144-16 \\ \Rightarrow h^{2}=128 \\ \Rightarrow h=\sqrt{128}=8 \sqrt{2} \text { सेमी }
शंकु का आयतन =\frac{1}{3} \pi r^{2} h \\ =\frac{1}{3} \times \frac{22}{7} \times(4)^{2} \times 8 \sqrt{2} \\ =\frac{3981.24}{21} \\ =189.61 \text { घन सेमी }
उपर्युक्त उदाहरणों के द्वारा शंकु का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cone) को समझ सकते हैं।
3.शंकु का पृष्ठीय क्षेत्रफल और आयतन की समस्याएं (Surface Area and Volume of Cone Problems):
(1.)यदि शंकु के आधार की त्रिज्या 21 सेमी तथा ऊँचाई 28 सेमी हो तो शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल और आयतन ज्ञात कीजिए।
(2.)एक टेन्ट शंकु के आकार का है।जिसके आधार की त्रिज्या 7 मीटर तथा ऊँचाई 5 मीटर है।टेन्ट में लगने वाले कपड़े का क्षेत्रफल ज्ञात कीजिए।
(3.)एक शंकु की त्रिज्या और ऊँचाई का अनुपात 3:4 हैं।यदि इसका आयतन 301.44 घनसेमी हो तो शंकु की त्रिज्या और तिर्यक ऊँचाई ज्ञात कीजिए।
(4.)एक शंकु की ऊँचाई 24 सेमी तथा वक्र पृष्ठीय क्षेत्रफल 550 वर्गसेमी है।इसका आयतन ज्ञात कीजिए।
उत्तर (Answers):(1.)सम्पूर्ण पृष्ठीय क्षेत्रफल=3696 वर्गसेमी, आयतन=12936 घनसेमी
(2.)189.2 वर्ग मीटर
(3.)त्रिज्या (r)=6 सेमी, तिर्यक ऊँचाई (l)=10 सेमी (4.)1232 घनसेमी
उपर्युक्त सवालों को हल करने पर शंकु का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cone) को आसानी से समझ सकते हैं।
4.मुख्य बातें (HIGHLIGHTS):
(1.)किसी ठोस आकृति के पृष्ठीय क्षेत्रफल से तात्पर्य समस्त पृष्ठों के क्षेत्रफल के योग से है।
(2.)किसी ठोस द्वारा आकाश (Space) या हवा में जितना स्थान घेरा जाता है वह उसका आयतन कहलाता है।
(3.)क्षेत्रफल को वर्ग इकाई व आयतन को घन इकाई में मापा जाता है।
(4.)लंबवृत्तीय शंकु वह ठोस आकृति है जब कोई रेखाखण्ड एक स्थिर बिन्दु पर एक स्थिर रेखा से अचर कोण पर परिक्रमण करती है।
(5.)यदि तिर्यक ऊँचाई को अक्ष के सापेक्ष परिक्रमण कराते हैं तो बन्द आधार वाला शंकु जनित होता है।
(6.)वृत्त के केंद्र और शंकु के शीर्ष को मिलाने वाली रेखा शंकु का अक्ष कहलाती है।
(7.)लंबवृत्तीय शंकु का अक्ष आधार पर लंबवत होता है।
(8.)क्षेत्रफल और आयतन की इकाईयां:
क्षेत्रफल की इकाई:
1वर्गसेमी=1सेमी×1सेमी=10 मिमी×10 मिमी=100 वर्गमिमी
1 वर्गमीटर=1मीटर×1मीटर=10 डेसीमीटर×10 डेसीमीटर=100 वर्ग डेसीमीटर
आयतन की इकाई:
1घनसेमी=1मिलीलीटर=1सेमी×1सेमी×1सेमी=10 मिमी×10 मिमी×10मिमी=1000 घनसेमी
1घनमीटर=1मीटर×1मीटर×1मीटर=100 सेमी×100 सेमी×100 सेमी=1000000 घनसेमी
1घनमीटर=1000 लीटर=1 किलोलीटर
Also Read This Article:-Surface Area and Volume of Cuboid
5.शंकु का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cone) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.आप एक शंकु का पृष्ठीय क्षेत्रफल और आयतन कैसे ज्ञात करते हैं? (How do you find the surface area and volume of a cone?):
उत्तर:त्रिज्या r और ऊँचाई h के संदर्भ में वृत्ताकार शंकु सूत्र:
एक शंकु का आयतन (Volume of a cone): V = (\frac{1}{3})πr^{2}h
एक शंकु की तिर्यक ऊँचाई (Slant height of a cone): s =\sqrt{(r^2 + h^2)}
शंकु का पार्श्व पृष्ठीय क्षेत्रफल (Lateral surface area of a cone): L=\pi rs =\pi r \sqrt{(r^2 + h^2)}
एक शंकु (एक वृत्त) का आधार पृष्ठीय क्षेत्रफल (Base surface area of a cone (a circle)): B =\pi r^{2}
एक शंकु का कुल पृष्ठीय क्षेत्रफल (Total surface area of a cone): A =L + B=\pi rs +π r^{2} =πr(s + r)= \pi r(r + \sqrt{(r^2 + h^2)})
प्रश्न:2.शंकु का पृष्ठीय क्षेत्रफल कितना है? (What is the surface area of the cone?):
उत्तर:एक लम्बवृत्तीय शंकु का पार्श्व पृष्ठीय क्षेत्रफल (lateral surface area) ज्ञात कीजिए,यदि त्रिज्या 4 सेमी है और तिरछी ऊंचाई 5 सेमी है।एक शंकु के कुल पृष्ठीय क्षेत्रफल का सूत्र (The formula for the total surface area of a right cone is) T.S.A=\pi rl+\pi r^{2} है।
प्रश्न:3.शंकु का सीएसए और टीएसए क्या है? (What is CSA and TSA of cone?):
उत्तर:यह वक्र सतह और शंकु के आधार के योग के बराबर होता है।एक शंकु के कुल पृष्ठीय क्षेत्रफल की गणना करने का सूत्र दिया गया है: कुल पृष्ठीय क्षेत्रफल (Total Surface Area) (TSA)=CSA+वृत्ताकार आधार का क्षेत्रफल (Area of Circular Base)।टीएसए (TSA)=πr (r+l)
प्रश्न:4.शंकु के आयतन का सूत्र क्या है? (What is the formula for volume of cones?):
उत्तर:एक शंकु के आयतन का सूत्र (The formula for the volume of a cone) V= (\frac{1}{3}) h \pi r^{2} है।
प्रश्न:5.एक शंकु की तिर्यक ऊँचाई कितनी होती है? (What is the slant height of a cone?):
उत्तर:किसी वस्तु की तिरछी ऊँचाई (slant height) (जैसे शंकु (cone) या पिरामिड (pyramid)) वक्र सतह के साथ दूरी है,जो शीर्ष पर किनारे से आधार पर वृत्त की परिधि (circumference) पर एक बिंदु तक खींची जाती है।
प्रश्न:6.शंकु का पृष्ठीय क्षेत्रफल क्यों होता है? (Why is the surface area of a cone?):
उत्तर:एक शंकु का पृष्ठीय क्षेत्रफल (surface area of a cone) वक्र पृष्ठीय क्षेत्रफल और आधार के क्षेत्र के बराबर है: \pi r^{2}+\pi Lr , जहां r शंकु का आधार की त्रिज्या को दर्शाता है और L शंकु की तिर्यक ऊंचाई को दर्शाता है।वक्र पृष्ठीय क्षेत्रफल (curved surface area) को पार्श्व पृष्ठीय क्षेत्रफल (lateral surface area) भी कहा जाता है।
प्रश्न:7.आप एक शंकु का CSA कैसे सिद्ध करते हैं? (How do you prove CSA of a cone?):
उत्तर:एक शंकु के वक्र पृष्ठीय क्षेत्रफल (curved surface area) और कुल पृष्ठीय क्षेत्रफल (total surface area) की गणना करने के लिए,हम इसे एक वृत्ताकार आधार (circular base) और शीर्ष तिरछे भाग (top slanted part) में विभाजित करते हैं।झुके हुए भाग का क्षेत्रफल आपको वक्र पृष्ठीय क्षेत्रफल देता है।कुल पृष्ठीय क्षेत्रफल इस वृत्ताकार आधार और वक्र पृष्ठीय क्षेत्रफलों का योग होता है।
प्रश्न:8.शंकु का आयतन क्यों होता है? (Why is the volume of a cone?):
उत्तर:मेरे लिए,इससे पता चला कि दूसरी डिस्क (second disk) को पहली डिस्क के आयतन के बराबर 4 सिलेंडरों (cylinders) में तोड़ा जा सकता है,तीसरे को 9 में,चौथे को 16 में और इसी तरह।तो एक शंकु का आयतन सभी सिलेंडरों के योग के पहले डिस्क के आयतन के बराबर होता है,जिसे हम वर्ग सूत्र के योग (summation of squares formula) का उपयोग करके प्राप्त कर सकते हैं।
प्रश्न:9.शंकु के छिन्नक का सूत्र क्या होता है? (What is the formula of frustum of cone?):
उत्तर: एक शंकु के छिन्नक (frustum of a cone) का वक्र पृष्ठीय क्षेत्रफल (CSA) है:=πl(R + r) जहाँ (r) का अर्थ=छोटे वृत्त की त्रिज्या और (R) का अर्थ=बड़े सर्कल की त्रिज्या है और (l)= छिन्नक की तिरछी ऊंचाई।
प्रश्न:10.एक शंकु की तिर्यक ऊँचाई और ऊँचाई में क्या अंतर है? (What is the difference between slant height and height of a cone?):
उत्तर:एक शंकु के तीन आयाम (three dimensions) होते हैं।ऊर्ध्वाधर ऊँचाई (या ऊँचाई) (vertical height (or altitude)) जो ऊपर से नीचे तक आधार की लंबवत दूरी है।तिरछी ऊँचाई (slant height) जो ऊपर से नीचे की ओर,आधार परिधि पर एक बिंदु तक की दूरी है।
प्रश्न:11.छिन्नक की तिर्यक ऊँचाई का सूत्र क्या होता है? (What is the formula of slant height of frustum?):
उत्तर:छिन्नक की तिरछी ऊंचाई (Slant height of the frustum)= \sqrt{h^2+(R−r)^2}
प्रश्न:12.आधे में काटे गए शंकु को क्या कहते हैं? (What is a cone cut in half called?):
उत्तर:ज्यामिति में,एक छिन्नक (frustum) (बहुवचन:फ्रस्टा (frusta) या फ्रस्टमस (frustums)) एक ठोस (आमतौर पर एक शंकु (cone) या पिरामिड(pyramid)) का हिस्सा होता है जो इसे काटने वाले एक या दो समानांतर समतलों के बीच स्थित होता है।
प्रश्न:13.आप एक शंकु की ऊंचाई कैसे ज्ञात करते हैं? (How do you find the height of a cone?),ज्यामिति में शंकु की ऊँचाई का सूत्र क्या है? (What Is Cone Height Formula in Geometry?):
उत्तर:शंकु की ऊंचाई सूत्र शंकु की ऊंचाई की गणना करता है।शंकु की ऊँचाई के सूत्रों का उपयोग करते हुए शंकु की ऊँचाई हैं, h=\frac{3V}{\pi r^{2}} और h^{2} = l^{2}-r^{2} , जहाँ V=शंकु का आयतन,r=शंकु की त्रिज्या और l = शंकु की तिरछी ऊँचाई।
प्रश्न:14.एक शंकु के R और L के बीच क्या संबंध है? (What is the relation between R and L of a cone?):
उत्तर:पाइथागोरस प्रमेय को शंकु पर लागू करके,हम शंकु के पृष्ठीय क्षेत्रफल (surface area) और उसकी ऊँचाई के बीच संबंध ज्ञात कर सकते हैं।हम जानते हैं, h^2 + r^2=l^2 जहाँ h शंकु की ऊँचाई (height of the cone) है,r आधार की त्रिज्या (radius of the base) है और l शंकु की तिर्यक ऊँचाई (slant height) है।
प्रश्न:15.एक शंकु की तिर्यक ऊँचाई और त्रिज्या के बीच गणितीय संबंध क्या है? (What is the mathematical relation between slant height height and radius of a cone?):
उत्तर:मान लीजिए कि शंकु की ऊँचाई (height) h है,तिरछी ऊँचाई (slant height) l है और त्रिज्या (radius) r है।चूँकि एक शंकु में ऊँचाई त्रिज्या के लंबवत होती है।या h^{2} = l^{2} - r^{2}
प्रश्न:16.छिन्नक का टीएसए क्या है? (What is TSA of frustum?):
उत्तर:इस प्रकार,लम्ब वृत्तीय शंकु के दिए गए छिन्नक का कुल पृष्ठीय क्षेत्रफल (total surface area of the given frustum) है, TSA=\pi L(R + r)+\pi (R^{2}+ r^{2})
प्रश्न:17.छिन्नक और रूण्डित में क्या अंतर है? (What is difference between frustum and truncated?):
उत्तर:संज्ञा के रूप में छिन्नक (frustum) और कटाव के बीच का अंतर यह है कि छिन्नक (frustum) एक शंकु (cone) या पिरामिड (pyramid) है जिसकी नोक (tip) को उसके आधार के समानांतर एक समतल द्वारा काट दिया गया है जबकि रूण्डित (सभी अर्थो में) को छोटा (truncating) या छोटा करने (shortening) का कार्य है।
उपर्युक्त प्रश्नों के उत्तर द्वारा शंकु का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cone) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा शंकु का पृष्ठीय क्षेत्रफल और आयतन (Surface Area and Volume of Cone) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
