Set Theory and Basic Notation Part -2
समुच्चय सिद्धान्त और बेसिक नोटेशन भाग-2 (Set Theory and Basic Notation Part-2)
- समुच्चय सिद्धान्त और बेसिक नोटेशन भाग-2 (Set Theory and Basic Notation Part-2 ) में समुच्चय सिद्धांत की बेसिक बातें बताई गई है.साथ ही उनके नोतेशन के बारे में बताया गया है.समुच्चय सिद्धांत आधुनिक युग की क्रांतिकारी खोज है.
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
1.संक्रिया ,संकेतन और वेन आरेखों का संक्षिप्त रूप (A Brief Look At Operations, Notation & Venn Diagrams),समुच्चय सिद्धान्त और बेसिक नोटेशन भाग-2 (Set Theory and Basic Notation Part-2 ):
- जैसा कि पिछले लेख में कहा गया है,सीखने के सिद्धांत में मूल लाभों में से एक किसी विशेष सिद्धांत से नहीं,बल्कि स्थापित भाषा से उपजा है।यही कारण है कि इस अनुवर्ती टुकड़े के थोक में बड़े पैमाने पर सेट सिद्धांत संकेतन, संचालन और दृश्य प्रतिनिधित्व शामिल हैं। एक सेट और इसके संबंधित तत्वों को नोट करने के लिए दो सबसे बुनियादी प्रतीकों को पेश करके किक को बंद करें।नीचे दी गई तालिका में तीन तत्वों के साथ एक उदाहरण सेट A,है:
- पहली पंक्ति तीन अलग तत्वों (A = {1,2,3}) के साथ ए सेट दिखाती है; दूसरी पंक्ति यह दर्शाने के सही तरीके को प्रदर्शित करती है कि एक एकल, कुछ तत्व,1,सेट A के अंतर्गत आता है।अभी तक सीधे आगे – लेकिन सेट सिद्धांत एक दूसरे सेट और यात्रा के दौरान आम तौर पर फेंकने से काफी अधिक दिलचस्प हो जाता है। संचालन।
- नीचे दी गई तालिका के लिए, दो माध्यमिक सेट B & C प्रस्तुत करें, जिनमें क्रमशः निम्नलिखित तत्व शामिल हैं: B = {3, A, B, C, D, E}, C = {1,2}। भले ही हमने कुल तीन सेट (A, B, और C) पेश किए हों, नीचे दिए गए उदाहरण संचालन एक समय में केवल दो सेटों के लिए होते हैं, इसलिए कृपया बाईं ओर के कॉलम पर नोट किए गए सेटों पर ध्यान दें । निम्न तालिका में पांच सबसे आम सेट ऑपरेंड हैं:
- और वहां हम जाते हैं, सेट थ्योरी में पांच सबसे आम ऑपरेशन; वे शुद्ध गणित से बाहर के डोमेन में भी काफी लोकप्रिय हैं। वास्तव में, इसकी अत्यधिक संभावना है कि आपने अतीत में इस प्रकार के ऑपरेशनों को देखा या निपटाया है, बस सटीक शब्दावली के बिना। इस मामले में, किसी भी स्कूल-ग्रेड के छात्र को दो इंटरसेप्टिंग समूहों के वेन आरेख का वर्णन करने के लिए कहें और वे सहज रूप से सही परिणाम पर पहुंचेंगे।
- अंतिम पंक्ति पर एक दूसरा नज़र डालें, सापेक्ष पूरक – क्या वह अजीब शब्द नहीं है? क्या वास्तव में सापेक्ष? यदि A – B के सापेक्ष पूरक को A और B नहीं के रूप में परिभाषित किया गया है, तो हम उस सब को कैसे निरूपित करते हैं जो B नहीं है?
Also Read This Article:What is mathematical reality and truth
2.यूनिवर्सल सेट और रिक्त सेट (The Universal Set The Empty Set):
- जैसा कि यह पता चला है, अगर हम एक सार्थक उत्तर पर पहुंचना चाहते हैं, तो हमें सबसे पहले अपने सेट की समस्या के ब्रह्मांड को कुछ संदर्भ प्रदान करना होगा। अक्सर एक समस्या की शुरुआत में स्पष्ट रूप से कहा गया है, जब किसी सेट के स्वीकार्य तत्वों को कुछ निश्चित वर्ग के ऑब्जेक्ट तक सीमित कर दिया जाता है, तो एक सार्वभौमिक सेट मौजूद होता है जो कि ग्रैंड-सेट होता है जिसमें उस विशेष समस्या के लिए सभी तत्व होते हैं। उदाहरण के लिए, यदि हम कड़ाई से अंग्रेजी-अक्षरों के सेट के साथ काम करना चाहते थे, तो हमारे सार्वभौमिक सेट यू में वर्णमाला के 26 अक्षर शामिल हैं।
- U के किसी भी सबसेट A के लिए, A के पूरक (A – या U – A के प्रतीक) को U के ब्रह्मांड के सभी तत्वों के सेट के रूप में परिभाषित किया गया है जो A में नहीं हैं। ऊपर दिए गए प्रश्न का संदर्भ देते हुए, B का पूरक। यूनिवर्सल सेट के भीतर वह सब कुछ है जो A सहित B नहीं है।
- इससे पहले कि हम आगे बढ़ें, एक और वैचारिक सेट है जो बुनियादी समझ के लिए बहुत महत्वपूर्ण है: अशक्त या खाली सेट। ध्यान दें कि यहां पसंद का व्याकरण जानबूझकर है। यह एक यात्रा है, लेकिन केवल एक खाली सेट है, इसलिए यह “खाली सेट है,” कभी भी “एक खाली सेट नहीं है।” जबकि समकक्षता इस टुकड़े के दायरे से परे है, यहां मूल सिद्धांत यह है कि दो सेट समान हैं यदि वे समान तत्व हैं; इसलिये बिना किसी तत्व के केवल एक सेट हो सकता है। इसलिए वहाँ एक खाली सेट है।
Also Read This Article:Set Notation
3.वेन आरेख और परे (Venn Diagrams & Beyond):
-
- Added:
- वेन आरेख, आधिकारिक तौर पर एक जॉन वेन द्वारा 1880 में आविष्कार किया गया था, ठीक वही है जिसकी आप कल्पना कर रहे हैं, हालांकि शैक्षणिक परिभाषा कुछ इस प्रकार है:
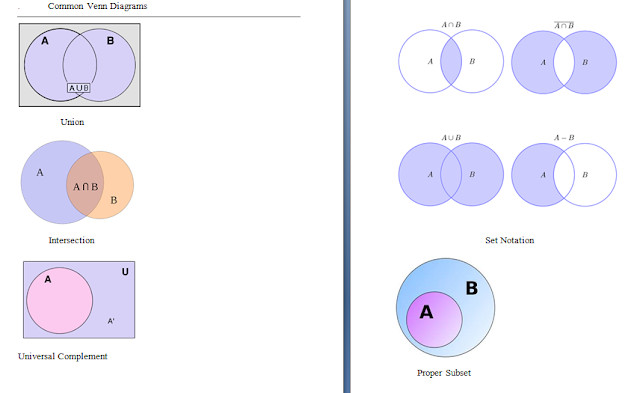
- वेन आरेख एक योजनाबद्ध आरेख है जो विभिन्न गणितीय सेटों के बीच सभी संभावित तार्किक संबंधों को दर्शाता है।
नीचे छह-सबसे आम वेन आरेखों का एक चित्र है, लगभग सभी प्रदर्शित करने वाले ऑपरेंड जिन्हें हमने हाल ही में कवर किया है:
- किसी सेट और उसके तत्वों के लिए बहुत ही मूल संकेतन के साथ शुरू करते हुए, अब हम ऊपर दिए गए विज़ुअल गाइड का उत्पादन करने के लिए मूल ऑपरेंड को कवर करते हैं। बायीं ओर नीचे, सिमिट्रिक डिफरेंस को छोड़कर, अन्य सभी ऑपरेशन कवर किए गए थे। ज्ञान में किसी भी अंतराल को न छोड़ने के लिए, सममित अंतर, जिसे डिसइन्कक्टिव यूनियन के रूप में भी जाना जाता है, बस उन तत्वों का समूह है जो किसी भी सेट में नहीं हैं और उनके चौराहे में नहीं हैं।
- हम इसे कार्डिनैलिटी की अवधारणा से जोड़कर देखेंगे। निरपेक्ष-मूल्य प्रतीक द्वारा निरूपित, एक सेट की कार्डिनैलिटी एक निर्दिष्ट सेट के भीतर निहित अद्वितीय तत्वों की मात्रा है। उपरोक्त उदाहरण में, हमारे तीन सेटों की कार्डिनैलिटी है: | A | = 3, | B | = 6, और | C | = 2. अगले टुकड़े तक जाने से पहले, विचार के लिए कुछ भोजन – कार्डिनैलिटी और संभावित उप-संख्याओं के बीच क्या संबंध है?
Also Read This Article:Logic theory and basic notation
- उपर्युक्त आर्टिकल में समुच्चय सिद्धान्त और बेसिक नोटेशन भाग-2 (Set Theory and Basic Notation Part-2 ) के बारे में बताया गया है.
Set Theory and Basic Notation Part-2
समुच्चय सिद्धान्त और बेसिक नोटेशन भाग-2
(Set Theory and Basic Notation Part-2)
Set Theory and Basic Notation Part-2
समुच्चय सिद्धान्त और बेसिक नोटेशन भाग-2 (Set Theory and Basic Notation Part-2 ) में
समुच्चय सिद्धांत की बेसिक बातें बताई गई है.साथ ही उनके नोतेशन के बारे में
बताया गया है.समुच्चय सिद्धांत आधुनिक युग की क्रांतिकारी खोज है.
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |