Ratio of Areas of Similar Triangles
1.समरूप त्रिभुजों के क्षेत्रफलों का अनुपात (Ratio of Areas of Similar Triangles),समरूप त्रिभुजों का क्षेत्रफल प्रमेय कक्षा 10 (Area of Similar Triangles Theorem Class 10):
समरूप त्रिभुजों के क्षेत्रफलों का अनुपात (Ratio of Areas of Similar Triangles) उनकी संगत भुजाओं के वर्गों के अनुपात अथवा ऊंचाइयों के वर्गो के अनुपात अथवा उनकी माध्यिकाओं के वर्गों के अनुपात के बराबर होता है।
इस आर्टिकल में भुजाओं के वर्गों के अनुपात तथा ऊंचाइयों के वर्गों के अनुपात के बराबर उनके क्षेत्रफलों के अनुपात को सिद्ध करेंगे और उस पर आधारित उदाहरणों के द्वारा इन प्रमेयों को समझेंगे।
समरूप त्रिभुज (Similar Triangle):दो त्रिभुज समरूप कहलाएंगे यदि उनके संगत कोण बराबर हों अथवा उनकी संगत भुजाएं समानुपाती हो अथवा एक त्रिभुज की दो भुजाएं दूसरे त्रिभुज की संगत दो भुजाओं के समानुपाती हो तथा उनके बीच का कोण दोनों त्रिभुजों में बराबर हो।
प्रमेय (Theorem):1.दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी कोई भी दो संगत भुजाओं के वर्गों के अनुपात के बराबर होता है।
दिया है (Given): \triangle ABC \sim \triangle DEF अर्थात्
\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}
सिद्ध करना है (To Prove):\frac{ \triangle ABC \text { का क्षेत्रफल }}{ \triangle DEF \text { का क्षेत्रफल } }=\frac{AB^{2}}{DE^{2}}=\frac{BC^{2}}{EF^{2}}=\frac{AC^{2}}{DF^{2}}
रचना (Construction):AL \perp BC तथा DM \perp EF खींचा।
उपपत्ति (Proof):\triangle ABC \sim \triangle DEF \\ \angle A=\angle D , \angle B=\angle E तथा \angle C=\angle F
तथा \frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF} \cdots(1)
अब \triangle ALB तथा \triangle DME में
\angle ALB=\angle DME=90^{\circ}
तथा \angle B=\angle E
कोण-कोण समरूपता गुणधर्म से (By AA Similarity Property)
\triangle ALB \sim \triangle DME \\ \Rightarrow \frac{AL}{DM}=\frac{AB}{DE} \cdots(2)
(1) तथा (2) से-
\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}=\frac{AL}{DM} \cdots(3) \\ \frac{ \triangle ABC \text { का क्षेत्रफल }}{ \triangle DEF \text { का क्षेत्रफल } }=\frac{ \frac{1}{2} \times BC \times AL }{ \frac{1}{2} \times EF \times DM } \\ =\frac{ BC \times AL }{ EF \times DM } \\ \frac{ BC \times BC }{ EF \times EF } [(3) से]
=\frac{BC^{2}}{EF^{2}}\\=\frac{AB^{2}}{DE^{2}}=\frac{BC^{2}}{EF^{2}}=\frac{AC^{2}}{DF^{2}} [(1) से]
\Rightarrow \frac{ \triangle ABC \text { का क्षेत्रफल }}{ \triangle DEF \text { का क्षेत्रफल } } =\frac{AB^{2}}{DE^{2}}=\frac{BC^{2}}{EF^{2}}=\frac{AC^{2}}{DF^{2}}
उपप्रमेय (Corollary):1.दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत ऊंचाइयों (Corresponding Altitudes) के वर्गों के अनुपात के बराबर होता है।
दिया है (Given): \triangle ABC \sim \triangle DEF अर्थात्
\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}
सिद्ध करना है (To Prove):\frac{ \triangle ABC \text { का क्षेत्रफल }}{ \triangle DEF \text { का क्षेत्रफल } }=\frac{AL^{2}}{DM^{2}}
रचना (Construction):AL \perp BC तथा DM \perp EF खींचा।
उपपत्ति (Proof):
\triangle ABC \sim \triangle DEF \\ \angle A=\angle D , \angle B=\angle E तथा \angle C=\angle F
तथा \frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF} \cdots(1)
अब \triangle ALB तथा \triangle DME में
\angle ALB=\angle DME=90^{\circ}
तथा \angle B=\angle E
कोण-कोण समरूपता गुणधर्म से (By AA Similarity Property)
\triangle ALB \sim \triangle DME \\ \Rightarrow \frac{AL}{DM}=\frac{AB}{DE} \cdots(2)
(1) तथा (2) से-
\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}=\frac{AL}{DM} \cdots(3) \\ \frac{ \triangle ABC \text { का क्षेत्रफल }}{ \triangle DEF \text { का क्षेत्रफल } }=\frac{ \frac{1}{2} \times BC \times AL }{ \frac{1}{2} \times EF \times DM } \\ =\frac{ BC \times AL }{ EF \times DM } \\= \frac{ AL \times AL }{ DM \times DM } [(3) से]
\Rightarrow \frac{ \triangle ABC \text { का क्षेत्रफल }}{ \triangle DEF \text { का क्षेत्रफल } }=\frac{AL^{2}}{DM^{2}}
उपप्रमेय (Corollary):2.दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत माध्यिकाओं के वर्गों के अनुपात के बराबर होता है।
उपप्रमेय (Corollary):3.दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनके संगत कोणों के अर्द्धक रेखाखण्डों (Angle Bisector Segments) के वर्गों के मध्य अनुपात के बराबर होता है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Similarity of Triangles
2.समरूप त्रिभुजों के क्षेत्रफलों का अनुपात के उदाहरण (Ratio of Areas of Similar Triangles Examples):
Example-1.यदि \triangle ABC \sim \triangle DEF और उनके क्षेत्रफल क्रमशः 64 वर्ग सेमी और 121 वर्ग सेमी है;यदि EF=15.4 सेमी हो तो BC ज्ञात कीजिए।
Solution–\triangle ABC \sim \triangle DEF
तथा \triangle ABC का क्षेत्रफल=64 वर्ग सेमी
तथा \triangle DEF का क्षेत्रफल=121 वर्ग सेमी
EF=15.4 सेमी
\triangle ABC \sim \triangle DEF \\ \frac{ ar \triangle ABC }{ ar \triangle DEF } =\frac{AB^{2}}{DE^{2}}=\frac{BC^{2}}{EF^{2}}=\frac{AC^{2}}{DF^{2}}
[यदि दो त्रिभुज समरूप हैं तो इनके क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के बराबर होता है]
\frac{64}{121}=\left(\frac{BC}{EF}\right)^{2} \\ \Rightarrow \left(\frac{8}{11}\right)^{2}=\left(\frac{BC}{EF}\right)^{2} \\ \Rightarrow \frac{8}{11}=\frac{BC}{EF} \\ \Rightarrow \frac{8}{11}=\frac{BC}{15.4} \\ \Rightarrow BC=\frac{15.4 \times 8 }{11} \\ \Rightarrow BC=11.2 सेमी
Example-2.एक ही आधार BC पर दो त्रिभुज ABC एवं DBC बने हैं।यदि AD व BC परस्पर O पर प्रतिच्छेद करे तो सिद्ध कीजिए
\frac{ \triangle ABC \text { का क्षेत्रफल }}{ \triangle DBC \text { का क्षेत्रफल } }=\frac{AO}{DO}
Solution-दिया है (Given): \triangle ABC तथा \triangle DBC एक ही आधार BC पर बने हैं तथा AD व BC एक दूसरे को O पर प्रतिच्छेद करते हैं।
सिद्ध करना है (To Prove):\frac{ \triangle ABC \text { का क्षेत्रफल }}{ \triangle DBC \text { का क्षेत्रफल } }=\frac{AO}{DO}
रचना (Construction):AE \perp BC तथा DF \perp BC खींचे।
उपपत्ति (Proof): \triangle DOF तथा \triangle AOE में
\angle AEO =\angle DFO=90^{\circ}
\angle AOE =\angle DOF (शीर्षाभिमुख कोण)
\triangle AOE \sim \triangle DOF
कोण-कोण समरूपता गुणधर्म से (By AA Similarity Property)
\frac{AE}{DF}=\frac{AO}{DO} \cdots(1) \\ \frac{ ar \triangle ABC}{ar \triangle DBC }=\frac{ \frac{1}{2} \times BC \times AE }{ \frac{1}{2} \times BC \times DF } \\= \frac{AE}{DF} \cdots(2)
(1) और (2) से-
\frac{ ar \triangle ABC}{ar \triangle DBC }=\frac{AO}{DO}
Example-3. \triangle ABC में DE \parallel BC एवं AD:DB=2:3 हो तो \triangle ADE एवं \triangle ABC के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
Solution–\triangle ADE तथा \triangle ABC में
DE \parallel BC \\ \angle ADE=\angle ABC (संगत कोण)
\angle A=\angle A(उभयनिष्ठ है)
कोण-कोण समरूपता गुणधर्म से (By AA Similarity Property)
\triangle ADE \sim \triangle ABC \\ \frac{AD}{DB}=\frac{2}{3} \\ \frac{DB}{AD}=\frac{3}{2} \\ \Rightarrow \frac{DB}{AD}+1=\frac{3}{2}+1 \\ \Rightarrow \frac{DB+AD}{AD} =\frac{3+2}{2} \\ \Rightarrow \frac{AB}{AD} =\frac{5}{2} \\ \Rightarrow \frac{AD}{AB} =\frac{2}{5} \cdots(1)\\ \triangle ADE \sim \triangle ABC \\ \Rightarrow \frac{ ar \triangle ADE }{ ar \triangle ABC } =\left(\frac{AD}{AB} \right )^{2}
[त्रिभुज समरूप हों तो उन त्रिभुजों का क्षेत्रफल उनकी भुजाओं के वर्गों के अनुपात के बराबर होता है।]
\frac{ ar \triangle ADE }{ ar \triangle ABC }=\left(\frac{2}{5} \right )^{2} [(1) से]
=\frac{4}{25}
ar \triangle ADE : ar \triangle ABC=4 : 25
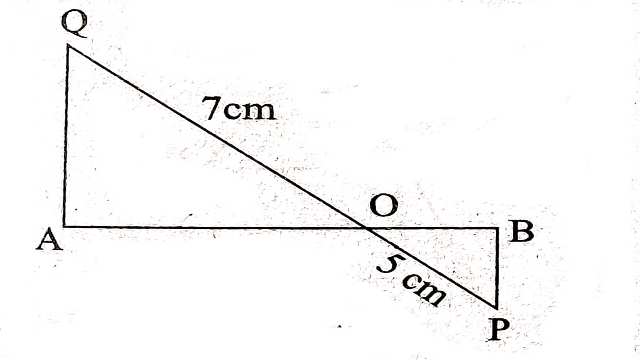
Example-4.रेखाखण्ड AB के बिन्दु A व B पर PB और QA लम्ब हैं।यदि P व Q;AB के दोनों ओर स्थित हों और P व Q को मिलाने पर वह AB को O पर प्रतिच्छेद करे तथा PQ=5 सेमी;QO=7 सेमी, \triangle POB का क्षेत्रफल 150 वर्ग सेमी हो तो \triangle QOA का क्षेत्रफल ज्ञात कीजिए।
Solution-दिया है (Given):रेखाखण्ड AB के बिन्दु A व B पर PB और QA लम्ब हैं।यदि P व Q;AB के दोनों ओर स्थित है तथा P व Q को मिलाने पर O पर प्रतिच्छेद करते हैं।
तथा PO=5 सेमी,QO=7 सेमी
\triangle POB का क्षेत्रफल=150 वर्ग सेमी
\triangle QAO तथा \triangle PBO में
\angle QAO=\angle PBO=90^{\circ}
\angle QOA=\angle POB (शीर्षाभिमुख कोण)
कोण-कोण समरूपता गुणधर्म से (By AA Similarity Property)
\triangle QAO \sim \triangle PBO \\ \frac{ ar \triangle QAO }{ ar \triangle PBO } =\left(\frac{OQ}{PO} \right )^{2}
[समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी भुजाओं के वर्गो के अनुपात के बराबर होता है।]
\frac{ ar \triangle QAO }{ 150 } =\left(\frac{7}{5} \right )^{2} \\ \Rightarrow \frac{ ar \triangle QAO }{ 150 } =\left(\frac{49}{25} \right ) \\ \Rightarrow ar \triangle QAO =\frac{49}{25} \times 150 \\ \Rightarrow ar \triangle QAO =49 \times 6 \\ \Rightarrow ar \triangle QAO =294 वर्ग सेमी
Example-5.आकृति में x का मान a,b एवं c के पदों में ज्ञात कीजिए।
Solution-BC=c,AB=b,AC=b+c
BD=x,AE=a,\angle A=50^{\circ} ,\angle B=50^{\circ}
\triangle CBD तथा \triangle CAE में
\angle CBD=\angle CAE=50^{\circ} (दिया है)
\angle C=\angle C(उभयनिष्ठ कोण)
(By AA Similarity Property)
\triangle CBD \sim \triangle CAE \\ \Rightarrow \frac{CB}{CA}=\frac{BD}{AE}
[समरूप त्रिभुजों की भुजाएं समानुपाती होती है।]
\frac{c}{b+c}=\frac{x}{a} [\because AC=AB+BC=b+c]
\therefore x=\frac{ac}{b+c}
Example-6. \triangle ABC में \angle B=90^{\circ} हो एवं BD कर्ण AC पर लम्ब हो तो सिद्ध कीजिए \triangle ADB \sim \triangle BDC है।
Solution-दिया है (Given): \triangle ABC में \angle B=90^{\circ} तथा BD \perp AC
सिद्ध करना है (To Prove):\triangle ADB \sim \triangle BDC
उपपत्ति (Proof):\angle ABC=90^{\circ} (दिया है)
\angle ABC + \angle BAC+\angle ACB=180^{\circ}(त्रिभुज के अन्त:कोण)
\Rightarrow 90^{\circ}+\angle BAC+\angle ACB=180^{\circ} \\ \Rightarrow \angle BAC+\angle ACB=90^{\circ} \cdots(1)
\triangle BDC में
\angle BDC=90^{\circ} \\ \angle BDC+\angle DBC+\angle BCD=180^{\circ} \\ 90^{\circ}+\angle DBC+\angle BCD=180^{\circ} \\ \Rightarrow \angle DBC+\angle BCD=90^{\circ} \cdots(2)
(1) और (2) से-
\angle BAC+\angle ACB=\angle DBC+\angle BCD \\ \Rightarrow \angle BAC+\angle ACB=\angle DBC+\angle ACB[ \because \angle ACB=\angle BCD ]\\ \Rightarrow \angle BAC=\angle DBC \cdots(3)
\triangle ADB तथा \triangle BDC में
\angle ADB=\angle BDC=90^{\circ} [\because BD \perp AC] \\ \angle BAC=\angle DBC[(3) से]
\therefore कोण-कोण समरूपता गुणधर्म से (By AA Similarity Property)
\triangle ADB \sim \triangle BDC
Example-7.सिद्ध कीजिए कि वर्ग की एक भुजा पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल उसी वर्ग के विकर्ण पर बनाए गए समबाहु त्रिभुज के क्षेत्रफल का आधा होता है।
Solution-दिया है (Given):ABCD एक वर्ग है।समबाहु त्रिभुज \triangle ABE वर्ग की भुजा AB पर स्थित है और समबाहु \triangle ACF वर्ग के विकर्ण AC पर स्थित है।
सिद्ध करना है (To Prove):ar \triangle ABE=\frac{1}{2} ar \triangle ACF
उपपत्ति (Proof):समकोण \triangle ABC में
AB^{2}+BC^{2}=AC^{2} \\ \Rightarrow AB^{2}+AB^{2}=AC^{2} [AB=BC वर्ग की भुजाएं]
\Rightarrow 2 AB^{2}=AC^{2} \\ \Rightarrow AC=\sqrt{2} AB \cdots(1)
\triangle ABE तथा \triangle ACF समबाहु त्रिभुज है इसलिए समकोणिक है।
\therefore \triangle ABE \sim \triangle ACF \\ \frac{ ar \triangle ABE }{ ar \triangle ACF} =\left(\frac{AB}{AC} \right )^{2}
[समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी भुजाओं के वर्गो के अनुपात के बराबर होता है।]
\therefore \frac{ ar \triangle ABE }{ ar \triangle ACF} =\left(\frac{AB}{\sqrt{2} AB} \right )^{2} \\ \Rightarrow \frac{ ar \triangle ABE }{ ar \triangle ACF} =\frac{1}{2} \\ \Rightarrow ar \triangle ABE=\frac{1}{2} ar \triangle ACF
उपर्युक्त उदाहरणों के द्वारा समरूप त्रिभुजों के क्षेत्रफलों का अनुपात (Ratio of Areas of Similar Triangles),समरूप त्रिभुजों का क्षेत्रफल प्रमेय कक्षा 10 (Area of Similar Triangles Theorem Class 10) को समझ सकते हैं।
3.समरूप त्रिभुजों के क्षेत्रफलों का अनुपात की समस्याएं (Ratio of Areas of Similar Triangles Problems):
(1.)दो समरूप त्रिभुजों के क्षेत्रफल क्रमशः 25 वर्ग सेमी एवं 36 वर्ग सेमी है।यदि छोटे त्रिभुज की माध्यिका 10 सेमी हो तो बड़े त्रिभुज की माध्यिका होगी।
(2.)एक समलम्ब चतुर्भुज ABCD में AB \parallel CD है एवं इसके विकर्ण O बिन्दु पर मिलते हैं।यदि AB=6 सेमी एवं CD=3 सेमी हो तो \triangle AOB के क्षेत्रफल एवं \triangle COD के क्षेत्रफल का अनुपात होगा।
(3.)यदि \triangle ABC \sim \triangle DEF हो एवं AB=10 सेमी,DE=8 सेमी हो तो \triangle ABC का क्षेत्रफल तथा \triangle DEF के क्षेत्रफल का अनुपात होगा।
(4.)यदि दो समरूप त्रिभुजों की ऊंचाइयों का अनुपात 4:9 हो तो दोनों त्रिभुजों के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
उत्तर (Answers):(1.)12 सेमी (2) ar \triangle AOB : ar \triangle COD=4:1 \\ (2) ar \triangle ABC : ar \triangle DEF=25 :16 (4.)16:81
उपर्युक्त सवालों को हल करने पर समरूप त्रिभुजों के क्षेत्रफलों का अनुपात (Ratio of Areas of Similar Triangles),समरूप त्रिभुजों का क्षेत्रफल प्रमेय कक्षा 10 (Area of Similar Triangles Theorem Class 10) को ठीक से समझा जा सकता है।
Also Read This Article:-Circle with Tangents
4.समरूप त्रिभुजों के क्षेत्रफलों का अनुपात (Ratio of Areas of Similar Triangles),समरूप त्रिभुजों का क्षेत्रफल प्रमेय कक्षा 10 (Area of Similar Triangles Theorem Class 10) के बारे में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1. दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात क्या है? (What is the ratio of the areas of two similar triangles?)
उत्तर-दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्ग के अनुपात के बराबर होता है।
∆ABC \sim ∆PQR=\frac{AB^2}{PQ^2}=\frac{BC^2}{QR^2}=\frac{AC^2}{PR^2}
प्रश्न:2.आप क्षेत्रफलों का अनुपात कैसे ज्ञात करते हैं? (How do you find the ratio of areas?)
उत्तर-समरूप त्रिभुजों के क्षेत्रफलों का अनुपात (Ratio of Areas of Similar Triangles) उनकी संगत भुजाओं के वर्गों के अनुपात अथवा ऊंचाइयों के वर्गो के अनुपात अथवा उनकी माध्यिकाओं के वर्गों के अनुपात के बराबर होता है।
प्रश्न:3.समरूप त्रिभुजों के क्षेत्रफलों का अनुपात संगत माध्यिकाओं के वर्गों के अनुपात के बराबर होता है (The ratio of areas of similar triangles is equal to the ratio of squares of corresponding medians)
उत्तर-हमें यह सिद्ध करना है कि दो समान त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत माध्यिकाओं के अनुपात के वर्ग के बराबर होता है।
जिस प्रकार ऊपर यह सिद्ध किया गया है कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के बराबर होता है उसी प्रकार यह सिद्ध किया जा सकता है कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी माध्यिकाओं के वर्गों के अनुपात के बराबर होता है।
इसलिए, दो समान त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत माध्यिकाओं के अनुपात के वर्ग के बराबर होता है।
प्रश्न:4.समरूप त्रिभुजों का क्षेत्रफल प्रमेय कक्षा 10 (Area of similar triangles Theorem Class 10)
उत्तर-समरूप त्रिभुजों के क्षेत्रफलों का अनुपात (Ratio of Areas of Similar Triangles) उनकी संगत भुजाओं के वर्गों के अनुपात अथवा ऊंचाइयों के वर्गो के अनुपात अथवा उनकी माध्यिकाओं के वर्गों के अनुपात के बराबर होता है।
प्रश्न:5. दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात के समानुपाती होता है (The ratio of areas of two similar triangles is proportional to)
उत्तर-उनकी संगत भुजाओं के वर्गों के अनुपात अथवा उनकी संगत ऊंचाइयों के वर्गो के अनुपात अथवा उनकी माध्यिकाओं के वर्गों के अनुपात से बराबर होता है।
प्रश्न:6.समरूप त्रिभुजों के क्षेत्रफलों का अनुपात संगत ऊंचाईयों के वर्गों के अनुपात के बराबर होता है (The ratio of areas of similar triangles is equal to the ratio of squares of corresponding altitudes)
उत्तर-हां यह सत्य है कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत ऊंचाइयों (Corresponding Altitudes) के वर्गों के अनुपात के बराबर होता है।
प्रश्न:7.जब दो त्रिभुज समरूप हों तो उनके क्षेत्रफल का अनुपात (When two triangles are similar the ratio of their area)
उत्तर-प्रमेय: यदि दो त्रिभुज समरूप हों,तो दोनों त्रिभुजों के क्षेत्रफल का अनुपात उनकी संगत भुजाओं के अनुपात के वर्ग के समानुपाती होता है।इससे सिद्ध होता है कि दो समरूप त्रिभुजों के क्षेत्रफल का अनुपात दोनों त्रिभुजों की संगत भुजाओं के वर्गों के समानुपाती होता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा समरूप त्रिभुजों के क्षेत्रफलों का अनुपात (Ratio of Areas of Similar Triangles),समरूप त्रिभुजों का क्षेत्रफल प्रमेय कक्षा 10 (Area of Similar Triangles Theorem Class 10) को समझ सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
