Circle with Tangents
1.वृत्त की स्पर्श रेखाएं (Circle with Tangents),एक वृत्त में कितनी स्पर्शरेखाएं हो सकती हैं?(How Many Tangents Can a Circle Have?)-
यहां वृत्त की स्पर्श रेखाओं (Circle with Tangents)से संबंधित विभिन्न प्रमेयों को सिद्ध किया गया है जिनके आधार पर प्रश्नों को हल किया जा सकता है।
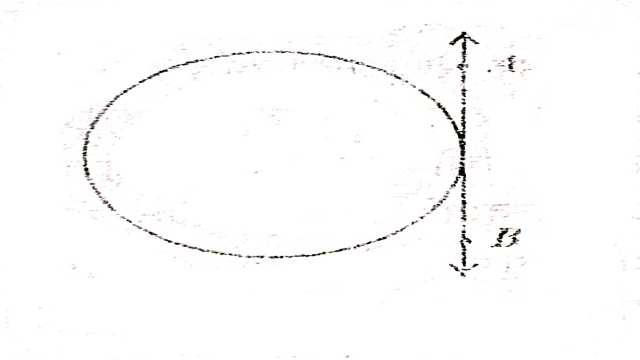
छेदक रेखा (Secant)-रेखा AB वृत्त को दो भिन्न-भिन्न बिंदुओं पर प्रतिच्छेद करती है।यह रेखा वृत्त को अधिकतम दो बिंदुओं पर ही प्रतिच्छेद कर सकती है क्योंकि वृत्त तीन या तीन से अधिक संरेखीय बिन्दुओं से नहीं गुजर सकता है। अतः एक ऐसी सरल रेखा जो वृत्त को दो भिन्न-भिन्न बिंदुओं पर प्रतिच्छेद करती है,छेदक रेखा (Secant) कहलाती है।
स्पर्श रेखा (Tangent)-रेखा AB वृत्त को दो संपाती बिंदुओं पर प्रतिच्छेद करती है अर्थात् रेखा वृत्त को एक बिंदु पर प्रतिच्छेद करती है अतः एक सरल रेखा जो वृत्त को केवल एक बिंदु पर स्पर्श करें,वृत्त की स्पर्श रेखा (Tangent) कहलाती है।वृत्त के समतल में स्पर्श रेखा और वृत्त में केवल एक बिंदु उभयनिष्ठ होता है।यह उभयनिष्ठ बिंदु स्पर्श बिंदु (Point of Contact) कहलाता है।
एक बिंदु से एक वृत्त पर स्पर्श रेखाओं की संख्या (Number of Tangents to a Circle from a point)-एक बिंदु से एक वृत्त पर कितनी स्पर्श रेखाएं खींची जा सकती है,यह वृत्त के सापेक्ष बिन्दु की स्थिति पर निर्भर करती है।यदि बिन्दु वृत्त पर स्थित है तो इस बिंदु से वृत्त की केवल एक स्पर्श रेखा खींची जा सकती है।
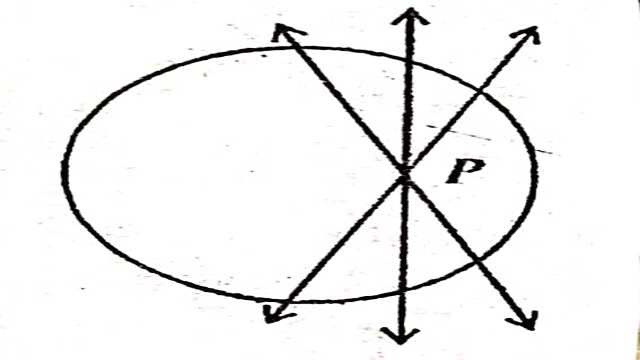
चित्र बिन्दु P वृत्त के अंदर स्थित है और इससे होकर जाने वाली कोई भी रेखा वृत्त को दो बिन्दुओं पर प्रतिच्छेद करती है।अतः यह रेखा स्पर्श रेखा नहीं हो सकती है।अर्थात् वृत्त के अंदर स्थित बिंदु से वृत की कोई भी स्पर्श रेखा नहीं खींची जा सकती है।
चित्र में बिंदु P वृत्त के बाहर स्थित है।यदि इस बिंदु से होकर जाने वाली एक छेदक रेखा खींची जाए तो यह वृत्त को दो बिंदुओं पर प्रतिच्छेद करेगी और वृत्त की जीवा को समाहित करेगी।इस जीवा की अधिकतम लंबाई वृत्त के व्यास के बराबर होगी।यदि छेदक रेखा को इस व्यास के दोनों ओर खींची जाए तो जीवा की लंबाई व्यास से कम होगी।यदि छेदक रेखा को P के सापेक्ष व्यास के दोनों ओर घुमाएं तो जीवा की लंबाई कम और कम होती जाएगी तथा प्रत्येक ओर एक स्थिति ऐसी आएगी कि जीवा छोटी होती-होती एक बिंदु बन जाएगी अर्थात् छेदक रेखा स्पर्श रेखा हो जाएगी।अतः वृत्त के एक बाह्य बिंदु से वृत पर दो स्पर्श रेखाएं खींची जा सकती।
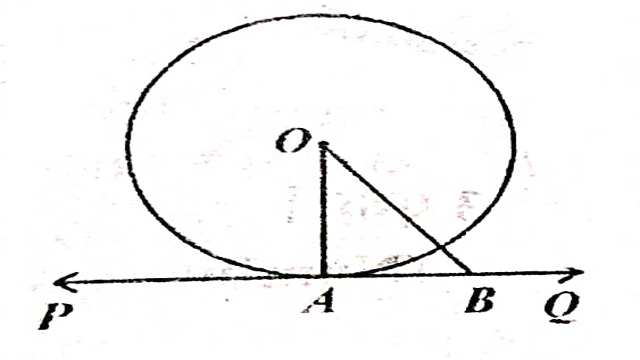
प्रमेय (Theorem):1.वृत्त के किसी बिंदु पर स्पर्श रेखा स्पर्श बिंदु से होकर जाने वाली त्रिज्या पर लम्बवत् होती है।
दिया है (Given):O केंद्र वाले वृत्त के बिंदु पर स्पर्श रेखा PQ है और बिंदु A से जाने वाली त्रिज्या OA है।
सिद्ध करना है (To Prove):OA \perp PQ
रचना (Construction):PQ पर A के अतिरिक्त कोई बिंदु B लेकर,OB को मिलाया।
उपपत्ति (Proof): बिंदु B वृत के बाहर है।क्योंकि स्पर्श बिंदु के अतिरिक्त स्पर्श रेखा पर स्थित प्रत्येक बिन्दु वृत के बाहर स्थित होता है।अतः स्पर्श बिंदु के अतिरिक्त स्पर्श रेखा पर स्थित प्रत्येक बिंदु की केंद्र से दूरी वृत्त की त्रिज्या से अधिक होगी।
अर्थात् OB>OA
अतः OA,उन सभी रेखाओं में जो O से PQ पर खींची जा सकती है सबसे छोटी है।
बिन्दु O को स्पर्श रेखा PQ के बिन्दुओं से मिलाने पर जितने रेखाखण्ड प्राप्त होते हैं उनमें सबसे छोटा रेखाखंड वह होता है जो कि O से PQ पर लंबवत हो।
अतः OA \perp PQ
प्रमेय (Theorem):2.(प्रमेय:1 का विलोम) सरल रेखा जो वृत्त पर दिए गए किसी बिंदु से खींची जाए और उस बिंदु से खींची गई त्रिज्या पर लम्बवत् हो,वृत्त की स्पर्श रेखा होती है।
दिया है (Given):चित्र में वृत्त का केन्द्र O और त्रिज्या OA है तथा OA \perp PQ है।
सिद्ध करना है (To Prove): रेखा PQ बिन्दु A वृत्त की स्पर्श रेखा है।
रचना (Construction):रेखा PQ पर अन्य बिन्दु B लेकर OB को मिलाया।
उपपत्ति (Proof): दिया है कि त्रिज्या OA रेखा PQ पर लम्बवत् हैं अतः O से PQ तक खींचे जा सकने वाले समस्त रेखाखण्डों में OA सबसे छोटा होता है
\Rightarrow OB>OA
अर्थात् बिन्दु B वृत्त के बाहर स्थित होगा।इसी प्रकार PQ के A के अतिरिक्त अन्य सभी बिन्दु वृत्त के बाहर स्थित होंगे। अतः रेखा PQ वृत्त को केवल एक बिन्दु पर प्रतिच्छेद करती, अतः PQ वृत्त की स्पर्श रेखा है।
प्रमेय (Theorem):3.किसी बाह्य बिन्दु से वृत्त पर खींची गई,दो स्पर्श रेखाओं की लम्बाईयां बराबर होती है।
दिया है (Given): वृत्त का केन्द्र O है और बाह्य बिन्दु से दो स्पर्श रेखाएं RP और RQ है।
सिद्ध करना है (To Prove):RP=RQ
रचना (Construction):OP,,OQ और OR मिलाया।
उपपत्ति (Proof): हम जानते हैं कि स्पर्श रेखा, वृत्त की त्रिज्या पर लम्बवत् होती है अतः
\angle OPR=\angle OQR=90^{\circ} …..(1)
अब \triangle OPR और \triangle OQR में
\angle OPR=\angle OQR=90^{\circ} [(1) से]
OR=OR (उभयनिष्ठ भुजा)
OP=OQ (एक ही वृत्त की त्रिज्याएं)
समकोण-कर्ण-भुजा सर्वांगसमता गुणधर्म से (By RHS Congruence Property)
\triangle OPR \cong \triangle OQR
अतः सर्वांगसम त्रिभुजों की संगत भुजाएं समान होंगी
\Rightarrow RP=RQ
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Basic Proportionality Theorem
2.वृत्त की स्पर्श रेखाओं के उदाहरण (Circle with Tangents Examples),स्पर्शरेखा सर्कल समस्याओं का समाधान (Tangent Circle Problems Solutions), वृत्त और स्पर्श रेखाओं की समस्याएं हल सहित (Problems on Circles and Tangents with Solutions)-
Example-1.दो संकेन्द्रीय वृत्तों की त्रिज्याएं 5 सेमी और 3 सेमी है।बड़े वृत्त की उस जीवा की लम्बाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो।
Solution-दो संकेन्द्रीय वृत्त जिनका कि एक केन्द्र O है तथा त्रिज्याएं क्रमशः 5 सेमी और 3 सेमी है।
माना कि PQ बड़े वृत्त की जीवा है जो छोटे वृत्त की स्पर्श रेखा है।
OM छोटे वृत्त की त्रिज्या है।
\therefore OM \perp PQ \\ \angle OMP=\angle OMQ =90^{\circ}
समकोण \triangle OMP और \triangle OMQ में
OM=OM (उभयनिष्ठ भुजा)
\angle OMP=\angle OMQ =90^{\circ}
OP=OQ (एक ही वृत्त की त्रिज्याएं)
समकोण-कर्ण-भुजा सर्वांगसमता गुणधर्म से (By RHS Congruence Property)
\triangle OMP \cong \triangle OMQ
PM=QM (सर्वांगसम त्रिभुजों की संगत भुजाएं बराबर होती है)
PQ=2 PM
\triangle OPM में
OP^{2}=OM^{2}+PM^{2} (बौधायन प्रमेय से)
\Rightarrow PM^{2}= OP^{2}-OM^{2} \\ \Rightarrow PM^{2}=5^{2}-3^{2} \\ \Rightarrow PM^{2}=25-9 \\ =16 \\ \Rightarrow PM=\sqrt{16} \\ \Rightarrow PQ=4 सेमी
PQ= 2 PM
\Rightarrow PQ=2 × 4=8 सेमी
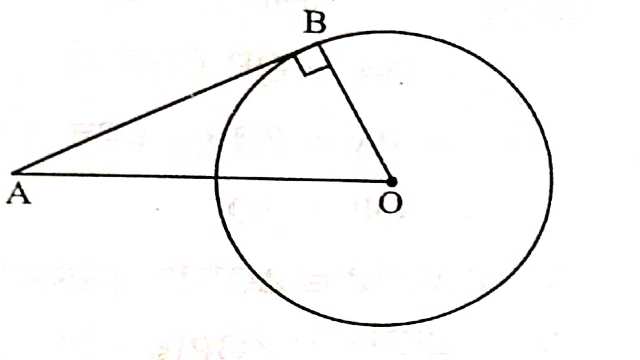
Example-2.किसी वृत्त के केन्द्र से 10 सेमी दूर स्थित किसी बिन्दु से वृत्त पर खींची गई स्पर्श रेखा की लम्बाई यदि 4 सेमी है तो वृत्त की त्रिज्या कितनी होगी?
Solution-एक वृत्त जिसका कि केन्द्र O है। वृत्त के केन्द्र से 10 सेमी दूर स्थित बिन्दु A है।
OA=10 सेमी,AB=4 सेमी
वृत्त की त्रिज्या तथा स्पर्श रेखा एक दूसरे पर लम्ब होती है।
OB \perp AB \\ \angle OBA=90^{\circ}
समकोण \triangle OBA में
OA^{2}=OB^{2}+AB^{2} \\ \Rightarrow OB^{2}=OA^{2}-AB^{2} \\ =10^{2}-4^{2} \\ =100-16 \\=84 \\ \Rightarrow OB=\sqrt{84} \\ \Rightarrow OB=2 \sqrt{21} सेमी
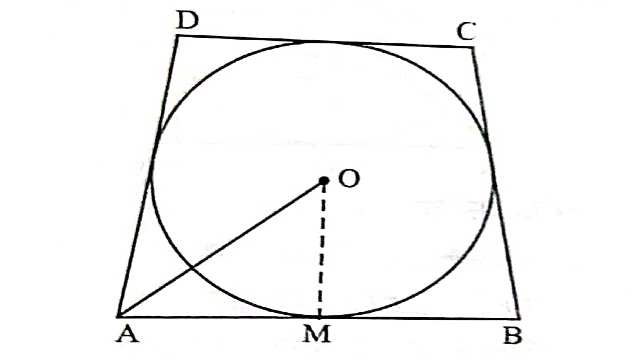
Example-3.एक O केन्द्र वाला वृत्त, चतुर्भुज ABCD की चारों भुजाओं को अन्त: स्पर्श इस प्रकार करता है कि यदि AB को स्पर्श बिन्दु 3:1 भागों में विभाजित करे तथा AB=8 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए जबकि OA=10 सेमी है।
Solution-एक वृत्त जिसका केन्द्र O है जो चतुर्भुज ABCD की चारों भुजाओं को अन्त: स्पर्श करता है।M बिन्दु AB को 3:1 में विभाजित करता है।
माना AM=3x
MB=x
\Rightarrow AB=AM+BM
8=3x+x
\Rightarrow 4x=8
\Rightarrow x=\frac{8}{4}
\Rightarrow x=2
AM=3x
\Rightarrow AM=3×2=6 सेमी
OA=10 सेमी
किसी वृत्त की त्रिज्या स्पर्श रेखा पर लम्ब होती है।
\therefore OM \perp AM \\ \angle OMA=90^{\circ}
अब \triangle OMA समकोण में
OA^{2}=OM^{2}+AM^{2} (बौधायन प्रमेय से)
\Rightarrow OM^{2}=OA^{2}-AM^{2} \\ =10^{2}-6^{2} \\ =100-36 \\=64 \\ \Rightarrow OM=\sqrt{64} \\ \Rightarrow OM=8
अतः वृत्त की त्रिज्या=8 सेमी
Example-4.एक वृत्त एक चतुर्भुज की सभी भुजाओं को स्पर्श करता है।सिद्ध कीजिए कि केन्द्र पर सम्मुख भुजाओं द्वारा अन्तरित कोण सम्पूरक होते हैं।
Solution-दिया है (Given):एक वृत्त जिसका केन्द्र O है।उसके परिगत चतुर्भुज बना है जो वृत्त को क्रमशः P,Q,R तथा S पर स्पर्श करता है।
सिद्ध करना है (To Prove):\angle AOB+\angle COD=180^{\circ} \\ \angle BOC+\angle AOD=180^{\circ}
रचना (Construction):OP,OQ,OR,OS तथा OA,OB,OC,OD को मिलाया।
उपपत्ति (Proof):\triangle OAP तथा \triangle OAS में
OP=OS (एक ही वृत्त की त्रिज्याएं)
OA=OA (उभयनिष्ठ भुजा)
AP=AS (वृत्त की स्पर्श रेखाएं)
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (By SSS Congruence Property)
\triangle OAP \cong \triangle OAS
\angle 1=\angle 8 (सर्वांगसम त्रिभुजों के संगत कोण)……(1)
इसी प्रकार सिद्ध कर सकते हैं कि
\angle 2=\angle 3 ....(2)\\ \angle 4=\angle 5.....(3) \\ \angle 6=\angle 7 ……(4)
हम जानते हैं कि किसी बिन्दु पर बनने वाले सभी कोणों का योग 360° होता है।
\angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6+\angle 7+\angle 8=360^{\circ} \\ \angle 1+\angle 2+\angle 2+\angle 5+\angle 5+\angle 6+\angle 6+\angle 1=360^{\circ} [(1),(2),(3),(4) से]
\Rightarrow 2(\angle 1+\angle 2+\angle 5+\angle 6)=360^{\circ} \\ \Rightarrow \angle 1+\angle 2+\angle 5+\angle 6=\frac{360^{\circ}}{2} \\ \Rightarrow (\angle 1+\angle 2)+(\angle 5+\angle 6)=180^{\circ} \\ \Rightarrow \angle AOB+ \angle DOC=180^{\circ}
इसी प्रकार सिद्ध कर सकते हैं कि
\angle AOB+ \angle DOC=180^{\circ}
अतः वृत्त के परिगत बने चतुर्भुज के आमने-सामने की भुजाएं केन्द्र पर सम्पूरक कोण अन्तरित करती हैं।
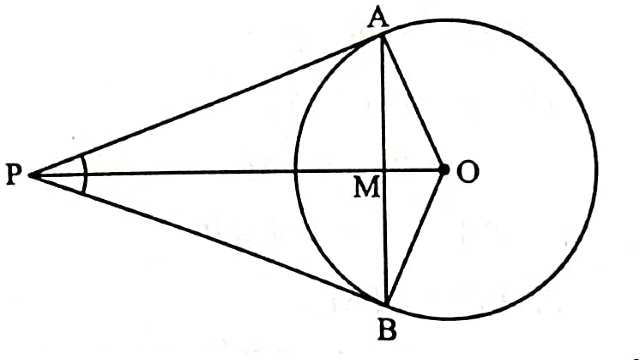
Example-5.आकृति में वृत्त का केन्द्र O है और बाह्य बिन्दु P से खींची गई स्पर्श रेखाएं PA और PB वृत्त को क्रमशः A व B पर स्पर्श करती हैं। सिद्ध कीजिए कि OP रेखाखण्ड AB का समद्विभाजक है।
Solution-दिया है (Given):एक वृत्त का केन्द्र O है और बाहरी बिन्दु P से खींची हुई स्पर्श रेखाएं PA और PB वृत्त को क्रमशः A व B पर स्पर्श करती हैं।
सिद्ध करना है (To Prove):OP रेखाखण्ड AB का समद्विभाजक है।
उपपत्ति (Proof): \triangle OAP तथा \triangle OBP में
OA=OB (एक ही वृत्त की त्रिज्याएं)
PA=PB (वृत्त की स्पर्श रेखाएं)
OP=OP (उभयनिष्ठ भुजा)
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (By SSS Congruence Property)
\triangle OAP \cong \triangle OBP
\angle OPA=\angle OPB (सर्वांगसम त्रिभुजों के संगत कोण)…….(1)
\triangle PAM तथा \triangle PBM में
PA=PB (वृत्त की स्पर्श रेखाएं)
PM=MP(उभयनिष्ठ भुजा)
\angle APM=\angle BPM
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)
\triangle APM \cong \triangle PBM
AM=BM (सर्वांगसम त्रिभुजों की संगत भुजाएं)
OP रेखाखण्ड AB का समद्विभाजक है।
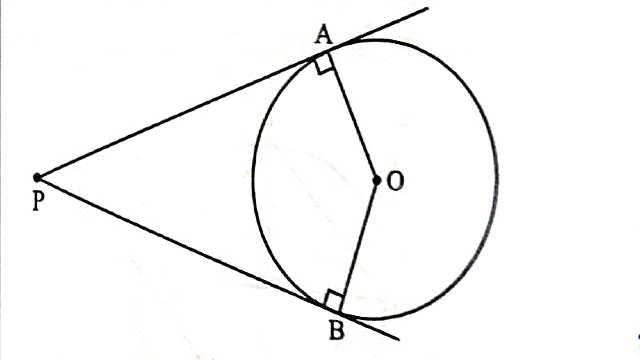
Example-6.आकृति में,बाह्य बिन्दु P से O केन्द्र वाले वृत्त को PA एवं PB दो स्पर्श रेखाएं क्रमशः A व B पर स्पर्श करती हैं।सिद्ध कीजिए कि PAOB चक्रीय चतुर्भुज है।
Solution-दिया है (Given):एक वृत्त जिसका केन्द्र O है।तथा बाह्य बिन्दु P से वृत्त की स्पर्श रेखा PA और PB खींची गई है।
सिद्ध करना है (To Prove):PAOB एक चक्रीय चतुर्भुज है।
उपपत्ति (Proof):स्पर्श रेखा तथा वृत्त की त्रिज्या स्पर्श बिन्दु पर लम्बवत् होती है।
OA \perp AP तथा OB \perp BP \\ \therefore \angle OAP=90^{\circ},\angle OBP=90^{\circ} ….(1)
किसी चतुर्भुज के चारों कोणों का योग 360° होता है।
चतुर्भुज OAPB में
\angle OAP+\angle APB +\angle PBO+\angle AOB=360^{\circ} \\ \Rightarrow 90^{\circ}+\angle APB + 90^{\circ}+\angle AOB=360^{\circ} [(1) से]
\Rightarrow \angle APB +\angle AOB=360^{\circ}-180^{\circ} \\ \Rightarrow \angle APB +\angle AOB=180^{\circ} ….(2)
(1) व (2) से-
\angle OAP+\angle OBP=180^{\circ} \\ \angle APB+\angle AOB=180^{\circ}
यदि किसी चतुर्भुज के सम्मुख कोण हों तो वह चतुर्भुज चक्रीय चतुर्भुज होता है।
उपर्युक्त उदाहरणों के द्वारा वृत्त की स्पर्श रेखाएं (Circle with Tangents),एक वृत्त में कितनी स्पर्शरेखाएं हो सकती हैं?(How Many Tangents Can a Circle Have?) को समझ सकते हैं।
3.वृत्त की स्पर्श रेखाओं की समस्याएं (Circle with Tangents Problems)-
(1.) सिद्ध कीजिए कि एक वृत्त की दो समान्तर स्पर्श रेखाओं के स्पर्श बिन्दुओं को मिलाने वाला रेखाखण्ड वृत्त का व्यास होता है।
(2.)एक वृत्त को बाह्य स्पर्श करता हुआ एक चतुर्भुज ABCD है। सिद्ध कीजिए कि AB+CD=AD+BC है।(अथवा) यदि एक चतुर्भुज की सभी भुजाएं किसी वृत्त को बाह्य स्पर्श करे तो सिद्ध कीजिए कि सम्मुख भुजाओं का योग परस्पर बराबर होता है।
(3.)चित्र में PA और PB उस वृत्त की स्पर्श रेखाएं हैं जिसका केन्द्र O है। वृत्त पर एक बिन्दु M हो तो सिद्ध कीजिए कि PL+PM=PN+MN है।
(4.)एक वृत्त ,\triangle ABC की भुजा BC को P पर स्पर्श करता है तथा AB और AC को बढ़ाए जाने पर Q और R स्पर्श करता है।
सिद्ध कीजिए कि AQ=\frac{1}{2}(\triangle ABC \text{ का परिमाप })
उपर्युक्त सवालों को हल करने पर वृत्त की स्पर्श रेखाएं (Circle with Tangents),एक वृत्त में कितनी स्पर्शरेखाएं हो सकती हैं?(How Many Tangents Can a Circle Have?) को ठीक से समझा जा सकता है।
Also Read This Article:-Loci And Concurrent Lines
4.वृत्त की स्पर्श रेखाएं (Circle with Tangents),एक वृत्त में कितनी स्पर्शरेखाएं हो सकती हैं?(How Many Tangents Can a Circle Have?) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न-
प्रश्न:1.वृत्त का स्पर्शरेखा बिंदु क्या है? (What is a Tangent Point of Circle?)
उत्तर-वृत्त की स्पर्शरेखा एक सीधी रेखा है जो केवल एक बिंदु पर वृत्त को स्पर्श करती है।इस बिंदु को स्पर्शरेखा का स्पर्शबिंदु कहा जाता है।वृत्त का स्पर्शरेखा,स्पर्शरेखा के स्पर्शबिंदु पर त्रिज्या के लंबवत होती है।
प्रश्न:2.स्पर्शरेखा स्पर्शरेखा प्रमेय क्या है? (What is Tangent Tangent Theorem?)
उत्तर-किसी बाह्य बिन्दु से वृत्त पर खींची गई,दो स्पर्श रेखाओं की लम्बाईयां बराबर होती है।
प्रश्न:3.यदि कोई रेखा किसी वृत्त की स्पर्शरेखा है तो आपको कैसे पता चलेगा? (How do you find if a Line is Tangent to a Circle?)
उत्तर-यह स्पर्श बाह्य बिन्दु से खींची जाती है तो स्पर्श रेखा तथा त्रिज्या बौधायन प्रमेय का पालन करती है।अर्थात् स्पर्श रेखा का वर्ग तथा त्रिज्या का वर्ग का योग उसके विकर्ण के वर्ग के बराबर होता है।
स्पर्श रेखा हमेशा त्रिज्या पर लम्बवत् होती है।
प्रश्न:4.एक सर्कल की स्पर्शरेखा की परिभाषा (Tangent of a Circle Definition)
उत्तर-यूक्लिडियन प्लेन ज्योमेट्री में, वृत्त की स्पर्श रेखा एक ऐसी रेखा होती है जो वृत्त को बिल्कुल एक बिंदु पर स्पर्श करती है, कभी भी वृत्त के आंतरिक भाग में प्रवेश नहीं करती है। वृत्त की स्पर्शरेखा रेखाएँ कई प्रमेयों का विषय बनती हैं, और कई ज्यामितीय रचनाओं और प्रमाणों में महत्वपूर्ण भूमिका निभाती हैं।
प्रश्न:5.एक वृत्त की दो स्पर्शरेखाएँ (Two Tangents to a Circle)
उत्तर-इस प्रमेय में कहा गया है कि यदि एक बाहरी बिंदु से,दो स्पर्शरेखा एक सर्कल में खींची जाती हैं, तो वे स्पर्शरेखाएं लम्बाई में बराबर होती हैं।स्पर्शरेखा खंड का अर्थ है बाहरी बिंदु और स्पर्शरेखा के बिंदु से जुड़ना।
प्रश्न:6.एक वृत्त प्रमेय की स्पर्शरेखा (Tangent to a Circle Theorem)
उत्तर-वृत्त के किसी बिंदु पर स्पर्श रेखा स्पर्श बिंदु से होकर जाने वाली त्रिज्या पर लम्बवत् होती है।
उपर्युक्त प्रश्नों के उत्तर द्वारा वृत्त की स्पर्श रेखाएं (Circle with Tangents),एक वृत्त में कितनी स्पर्शरेखाएं हो सकती हैं?(How Many Tangents Can a Circle Have?) को ठीक से समझ सकते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा वृत्त की स्पर्श रेखाएं (Circle with Tangents),एक वृत्त में कितनी स्पर्शरेखाएं हो सकती हैं?(How Many Tangents Can a Circle Have?) को ठीक से समझ सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
