Pythagoras Theorem
1.पाइथागोरस प्रमेय (Pythagoras Theorem),पाइथागोरस प्रमेय सूत्र (Pythagoras Theorem Formula):
पाइथागोरस प्रमेय (Pythagoras Theorem):पाइथागोरस समीकरण एक समकोण त्रिभुज की भुजाओं को सरल तरीके से जोड़ता है,ताकि यदि किन्हीं दो भुजाओं की लंबाई ज्ञात हो तो तीसरी भुजा की लंबाई को ज्ञात किया जा सकता है।
(1.)पाइथागोरस प्रमेय कथन (Pythagoras Theorem Statement):
किसी भी समकोण में,कर्ण का वर्ग शेष दोनों भुजाओं के वर्गो के योग के बराबर होता है।
पाइथागोरस प्रमेय प्रमाण (Pythagoras Theorem Proof),पाइथागोरस प्रमेय प्रमाण सरल (Pythagoras Theorem Proof Simple):
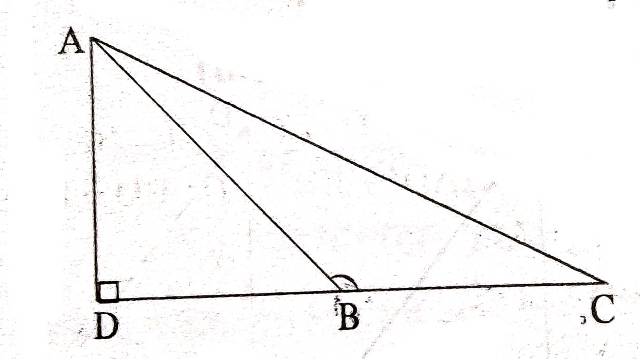
दिया है (Given):एक त्रिभुज \triangle ABC में \angle B=90^{\circ} है।
सिद्ध करना है (To Prove):AC^{2}=AB^{2}+BC^{2}
रचना (Construction):BD \perp AC खींचा।
उपपत्ति (Proof): \triangle ABC और \triangle ADB में
\angle ABC=\angle ADB=90^{\circ}
\angle A=\angle A(उभयनिष्ठ कोण है)
कोण-कोण समरूपता उपप्रमेय से (By AA Similarity Corollary)
\triangle ABC \sim \triangle ADB \\ \Rightarrow \frac{AB}{AD}= \frac{AC}{AB} (समरूप त्रिभुजों की संगत भुजाएं समानुपाती होती है)
\Rightarrow AB^{2}=AC \times AD \cdots(1)
इसी प्रकार \triangle ABC \sim \triangle BDC
\Rightarrow \frac{BC}{DC}= \frac{AC}{BC} \\ \Rightarrow BC^{2}=AC \times DC \cdots(2)
समीकरण (1) व (2) को जोड़ने पर-
\Rightarrow AB^{2}+BC^{2}=AC \times AD +AC \times DC \\ =AC(AD+DC) \\ =AC \times AC \\ =AC^{2} \\ \Rightarrow AB^{2}+BC^{2}=AC^{2}
(2.)पाइथागोरस प्रमेय का विलोम (Converse of Pythagoras Theorem):
यदि किसी त्रिभुज में सबसे लम्बी भुजा का वर्ग,शेष दोनों भुजाओं के वर्गों के योग के बराबर हो तो सबसे लम्बी भुजा के सम्मुख कोण का मान 90° (एक समकोण) अर्थात् यह त्रिभुज एक समकोण त्रिभुज होगा।
दिया है (To Given):\triangle ABC में AC^{2}=AB^{2}+BC^{2}
सिद्ध करना है (To Prove):\angle ABC=90^{\circ}
रचना (Construction): एक अन्य त्रिभुज DEF इस प्रकार बनाइए कि DE=AB,EF=BC तथा \angle E=90^{\circ}
उपपत्ति (Proof): \triangle DEF में \angle E=90^{\circ} (रचना से)
DE^{2}+EF^{2}=DF^{2} \\ AB^{2}+BC^{2}=DF^{2} (रचना से)
AB^{2}+BC^{2}=AC^{2}(दिया है)
\Rightarrow AC^{2}=DF^{2} \\ AC=DF \cdots(1)
इस प्रकार \triangle ABC तथा \triangle DEF में
AB=DE(रचना से)
BC=EF(रचना से)
AC=DF[(1) से]
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (By SSS Congruence Property)
\triangle ABC \cong \triangle DEF \\ \Rightarrow \angle B= \angle E \\ \angle E=90^{\circ} \\ \Rightarrow \angle B=90^{\circ}
\therefore \triangle ABC समकोण त्रिभुज है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Ratio of Areas of Similar Triangles
2.पाइथागोरस प्रमेय के उदाहरण (Pythagoras Theorem Examples):
Example-1.आकृति \triangle ABC में \angle B=90^{\circ} तथा D,BC का मध्यबिन्दु है। सिद्ध करो कि AC^{2}=AD^{2}+3 CD^{2}
Solution-दिया है (Given): \triangle ABC जिसमें \angle B=90^{\circ} और D,BC का मध्यबिन्दु है।
सिद्ध करना है (To Prove):AC^{2}=AD^{2}+3 CD^{2}
रचना (Construction):AD को मिलाया।
उपपत्ति (Proof):\triangle ABC में ,\angle B=90^{\circ}
AC^{2}=AB^{2}+BC^{2}(पाइथागोरस प्रमेय से)….(1)
\triangle ABD में
AD^{2}=AB^{2}+BD^{2} \\ AB^{2}=AD^{2}-BD^{2} \cdots(2)
समीकरण (1) व (2) से
AC^{2}=AD^{2}-BD^{2}+BC^{2} \\ \Rightarrow AC^{2}=AD^{2}-BD^{2}+(2 CD)^{2}
[BD=DC;D,BC का मध्यबिन्दु है। 2DC=BC]
\Rightarrow AC^{2}=AD^{2}-CD^{2}+4 CD^{2} \\ \Rightarrow AC^{2}=AD^{2}+3 CD^{2}
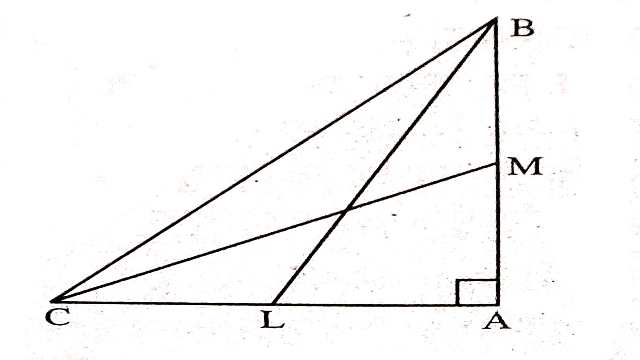
Example-2.\triangle ABC में \angle A=90^{\circ} तथा BL और CM क्रमशः \triangle ABC की माध्यिकाएं हैं।सिद्ध करना है 4(BL^{2}+CM^{2})=5 BC^{2}
Solution-दिया है (Given): \triangle ABC जिसमें \angle A=90^{\circ} और BC व CM माध्यिकाएं हैं।
सिद्ध करना है (To Prove):4(BL^{2}+CM^{2})=5 BC^{2}
उपपत्ति (Proof): \triangle ABC में \angle A=90^{\circ}
BC^{2}=AB^{2}+AC^{2}(पाइथागोरस प्रमेय से) …….(1)
\triangle BAL में \angle A=90^{\circ}
BL^{2}=AL^{2}+AB^{2}(पाइथागोरस प्रमेय से)
(\because L,AC का मध्य-बिन्दु है)
BL^{2}=\left ( \frac{1}{2}AC \right )^{2} +AB^{2} \\ \Rightarrow BL^{2}=\frac{1}{4} AC^{2}+AB^{2} \\ \Rightarrow 4 BL^{2}=AC^{2}+4 AB^{2} \cdots(2)
\triangle CAM में \angle A=90^{\circ} \\ CM^{2}=AM^{2}+AC^{2} \\ \Rightarrow CM^{2}=\left ( \frac{1}{2}AB \right )^{2} +AC^{2} \\ \Rightarrow CM^{2}= \frac{1}{4} AB^{2} +AC^{2} \\ \Rightarrow 4 CM^{2}= AB^{2} +4 AC^{2} \cdots(3)
समीकरण (2) और (3) को जोड़ने पर-
4 BL^{2}+4 CM^{2}=AC^{2}+4 AB^{2}+AB^{2}+4 AC^{2} \\ \Rightarrow 4(BL^{2}+CM^{2})=5 AB^{2}+5 AC^{2} \\ \Rightarrow 4(BL^{2}+CM^{2})=5 (AB^{2}+AC^{2}) \\ \Rightarrow 4(BL^{2}+CM^{2})=5 BC^{2} [(1) से]
Example-3.दी गई आकृति में O बिन्दु आयत ABCD के अन्दर स्थित है।सिद्ध करो OB^{2}+OD^{2}=OA^{2}+OC^{2}
Solution-दिया है (Given):O एक बिन्दु आयत ABCD के अन्तर्गत है।
सिद्ध करना है (To Prove):OB^{2}+OD^{2}=OA^{2}+OC^{2}
रचना (Construction): PQ \parallel BC खींची।
उपपत्ति (Proof):ABCD एक आयत है।
\angle B=\angle C=90^{\circ} \\ AD \parallel BC तथा AB \parallel DC
PQ \parallel BC (रचना से)
PQ \parallel AD \parallel BC \\ BC \perp AB और BC \parallel PQ \\ PQ \perp AB
इसी प्रकार PQ \perp DC \\ \angle APO = \angle BPO =\angle CQO= \angle DQO=90^{\circ}
\therefore APQD और BPQC आयत हैं।
AP=DQ और BP=CQ
समकोण \triangle BPO में OB^{2}=OP^{2}+BP^{2} (पाइथागोरस प्रमेय से)
OB^{2}=OP^{2}+CQ^{2} (\because BP=CQ)....(1)
समकोण \triangle DQO में
OD^{2}=OQ^{2}+DQ^{2} (पाइथागोरस प्रमेय से)
\Rightarrow OD^{2}=OQ^{2}+AP^{2} (\because DQ=AP)....(2)
समकोण \triangle APQ में
OA^{2}=OP^{2}+AP^{2} (पाइथागोरस प्रमेय से)…..(3)
समकोण \triangle CQO में
OC^{2}=OQ^{2}+CQ^{2} (पाइथागोरस प्रमेय से)…..(4)
समीकरण (1) और (2) को जोड़ने पर-
OB^{2}+OD^{2}=OP^{2}+CQ^{2}+OQ^{2}+AP^{2} \\ =(OP^{2}+AP^{2})+(CQ^{2}+OQ^{2}) \\=OA^{2}+OC^{2} [(3) और (4) से]
\Rightarrow OB^{2}+OD^{2}=OA^{2}+OC^{2}
Example-4.एक त्रिभुज ABC जिसमें \angle C समकोण है। भुजाओं CA और CB पर क्रमशः बिन्दु D और E स्थित है। सिद्ध कीजिए AE^{2}+BD^{2}=AB^{2}+DE^{2}
Solution-दिया है (Given): त्रिभुज \triangle ABC में,\angle C समकोण है तथा भुजा CA एवं CB पर क्रमशः D एवं E बिन्दु हैं।
सिद्ध करना है (To Prove):AE^{2}+BD^{2}=AB^{2}+DE^{2}
उपपत्ति (Proof):समकोण \triangle ACB में
AB^{2}=AC^{2}+CB^{2} (पाइथागोरस प्रमेय से)
समकोण \triangle DCE में
DE^{2}=DC^{2}+CE^{2} (पाइथागोरस प्रमेय से)
समीकरण (1) व (2) को जोड़ने पर-
AB^{2}+DE^{2}=AC^{2}+CB^{2}+DC^{2}+CE^{2} \\ =(AC^{2}+CE^{2})+(BC^{2}+CD^{2}) \\ AB^{2}+DE^{2} =AE^{2}+BD^{2} \\ \left [ \because AE^{2}=AC^{2}+CE^{2}, BD^{2}=BC^{2}+CD^{2}\right ]
[पाइथागोरस प्रमेय से]
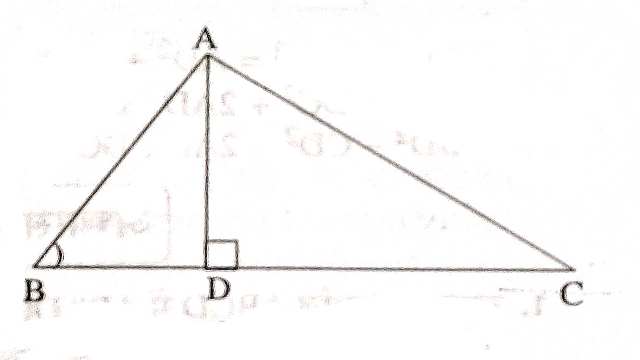
Example-5.चित्र AD \perp BC में है सिद्ध कीजिए कि AB^{2}+CD^{2}=BD^{2}+AC^{2}
Solution-दिया है (Given):\triangle ABC में AD \perp BC
सिद्ध करना है (To Prove):AB^{2}+CD^{2}=BD^{2}+AC^{2}
उपपत्ति (Proof):\triangle ADC में
AC^{2}=AD^{2}+CD^{2} (पाइथागोरस प्रमेय से)
\triangle ADB में
AB^{2}=AD^{2}+BD^{2} (पाइथागोरस प्रमेय से)
समीकरण (2) में से (1) घटाने पर-
\Rightarrow AB^{2}-AC^{2}=AD^{2}+BD^{2}-AD^{2}-CD^{2} \\ \Rightarrow AB^{2}-AC^{2}=BD^{2}-CD^{2} \\ \Rightarrow AB^{2}+CD^{2}=BD^{2}+AC^{2}
Example-6.BL और CM एक समकोण \triangle ABC त्रिभुज की माध्यिकाएं हैं तथा त्रिभुज में कोण A समकोण है।सिद्ध कीजिए कि
4(BL^{2}+CM^{2})=5 BC^{2}
Solution-दिया है (Given):\triangle ABC में \angle A=90^{\circ} ,CM तथा BL माध्यिकाएं हैं।
सिद्ध करना है (To Prove):4(BL^{2}+CM^{2})=5 BC^{2}
उपपत्ति (Proof):\triangle ABC में
BC^{2}=AB^{2}+AC^{2} (पाइथागोरस प्रमेय से)…..(1)
\triangle ABL में
BL^{2}=AL^{2}+AB^{2} (पाइथागोरस प्रमेय से)…..(2) (AL=\frac{1}{2} AC) \\ \Rightarrow BL^{2}=\left ( \frac{AC}{2} \right )^{2}+AB^{2} \\ =\frac{AC^{2}}{4}+AB^{2} \\ \Rightarrow 4 BL^{2}=AC^{2}+4AB^{2} \cdots(2)
\triangle CMA में
CM^{2}=AC^{2}+AM^{2} \\ \left [ \because AM=\frac{1}{2}AB \right ] \\ \Rightarrow CM^{2}=AC^{2}+\left ( \frac{AB}{2} \right )^{2}\\ =AC^{2}+\frac{AB^{2}}{4} \\ \Rightarrow 4 CM^{2}=4 AC^{2}+AB^{2} \cdots(3)
समीकरण (2) व (3) को जोड़ने पर-
4 BL^{2}+4 CM^{2}=AC^{2}+4 AB^{2}+4AC^{2}+AB^{2} \\ \Rightarrow 4(BL^{2}+CM^{2})=5 AB^{2}+5 AC^{2} \\ \Rightarrow 4(BL^{2}+CM^{2})=5 BC^{2}[(1) से]
उपर्युक्त उदाहरणों के द्वारा पाइथागोरस प्रमेय (Pythagoras Theorem),पाइथागोरस प्रमेय सूत्र (Pythagoras Theorem Formula) को समझ सकते हैं।
3.पाइथागोरस प्रमेय के सवाल (Pythagoras Theorem Questions):
(1.) \triangle ABC एक समद्विबाहु समकोण त्रिभुज है जिसका कोण C समकोण है।सिद्ध कीजिए कि AB^{2}=2 AC^{2}
(2.)किसी \triangle ABC में AD \perp BC तथा AD^{2}=BD \times CD है।सिद्ध कीजिए कि \triangle ABC एक समकोण त्रिभुज है।
(3.)आकृति में \triangle ABC एक अधिक कोण त्रिभुज है जिसका \angle B अधिक कोण है।यदि AD \perp CB ,तो सिद्ध कीजिए कि AC^{2}=AB^{2}+BC^{2}+2 BC \times BD
(4.)आकृति में \triangle ABC का \angle B न्यून कोण है।यदि AD \perp BC तो सिद्ध कीजिए कि AC^{2}=AD^{2}+BC^{2}-2 BC \times BD
उपर्युक्त सवालों को हल करने पर पाइथागोरस प्रमेय (Pythagoras Theorem),पाइथागोरस प्रमेय सूत्र (Pythagoras Theorem Formula) को ठीक से समझा जा सकता है।
Also Read This Article:-Similarity of Triangles
4.पाइथागोरस प्रमेय (Pythagoras Theorem),पाइथागोरस प्रमेय सूत्र (Pythagoras Theorem Formula) के बारे में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.पाइथागोरस प्रमेय क्या है? (What is Pythagoras Theorem?),पाइथागोरस की प्रमेय क्या है? (What is the Theorem of Pythagoras?):
उत्तर-पाइथागोरस प्रमेय एक गणितीय नियम है जो बताता है कि समकोण त्रिभुज की दो छोटी भुजाओं की लंबाई के वर्गों का योग कर्ण के वर्ग के बराबर होता है।
आज से लगभग ढाई हजार साल पहले प्रसिद्ध गणितज्ञ पाइथागोरस ने यूनान में ज्यामिति की नींव रखी थी।बाद में यूक्लिड ने अपनी प्रसिद्ध पुस्तक में उक्त प्रमेय का उल्लेख किया था।आज सारे विश्व में जो ज्यामिति पढ़ाई जाती है वह थोड़े हेरफेर के साथ यूक्लिड की ही ज्यामिति पढ़ाई जाती है।यूक्लिड ने बड़े ही तार्किक ढंग से ज्यामिति की रचना की है।इसलिए आज भी संसार में ज्यामिति का अध्ययन उसी ढंग से होता है।
परन्तु जो प्रमेय पाइथागोरस प्रमेय के नाम से प्रसिद्ध है,उस प्रमेय को पाइथागोरस से भी पहले हमारे भारत में बौधायन ने पता लगा लिया था।इस प्रमेय का उल्लेख बौधायन-शुल्वसूत्र में मिलता है।इसलिए हमारे विद्यालयों में इसी प्रमेय को बौधायन प्रमेय के नाम से पढ़ाया जाता है।
प्रश्न:2.पाइथागोरस द्वारा प्रयुक्त सूत्र क्या है? (What is the formula used by Pythagoras?):
उत्तर-पाइथागोरस के अनुसार किसी भी समकोण त्रिभुज की दो भुजाएं ज्ञात हो तो तीसरी भुजा की लम्बाई ज्ञात की जा सकती है।इसको सूत्र रूप में निम्न प्रकार व्यक्त किया जा सकता है-
a^2+b^2=c^2
परन्तु जिस समय पाइथागोरस ने यह सूत्र दिया था उसे उस समय अपरिमेय संख्याओं का ज्ञान नहीं था।लेकिन बाद में पाइथागोरस या उसके किसी शिष्य को पता चला कि ऐसी संख्याओं का भी अस्तित्व है जो परिमेय नहीं है।परन्तु पाइथागोरस ने इस रहस्य को बाहर के लोगों के सामने प्रकट नहीं किया।लेकिन यह बात बहुत दिनों तक छिपी हुई नहीं रह सकी।अन्त में यूनान के विद्वानों को इस बात का पता चल ही गया।
पाइथागोरस या उसके किसी शिष्य को इस बात का पता इस प्रकार चला कि जैसे यदि समकोण त्रिभुज की छोटी दोनों भुजाओं का मान 1,1 हो तो कर्ण का मान अपरिमेय संख्या प्राप्त होती है-
\sqrt{ 1^2+1^2}=\sqrt 2
प्रश्न:3.पाइथागोरस प्रमेय उदाहरण क्या है? (What is Pythagoras Theorem Example?):
उत्तर-पाइथागोरस प्रमेय के कई उदाहरण दिए जा सकते हैं-
3^2+4^2=5^2 \\ 5^2+12^2=13^2 \\ 8^2+15^2=17^2
हमारे देश के शूल्वसूत्रकार इस सम्बन्ध को अच्छी तरह से जानते थे।शुल्वसूत्र ग्रंथों में इस प्रकार के अनेक सम्बन्ध मिलते हैं।
प्रश्न:4.पाइथागोरस प्रमेय कथन (Pythagoras Theorem Statement):
उत्तर-पाइथागोरस मूल नियम यह था कि किसी भी आयत के विकर्ण पर खींचा गया वर्ग क्षेत्रफल में उन दोनों वर्गों के योग के समान होता है जो दोनों भुजाओं पर खींचे जाए।जिसका भावार्थ यही निकलता है कि समकोण त्रिभुज में कर्ण की लम्बाई का वर्ग इसकी शेष दो भुजाओं की लम्बाइयों के वर्गो के योग के बराबर होता है।
पाइथागोरस का विश्वास था संसार की सारी वस्तुओं को संख्याओं में व्यक्त किया जा सकता है।इसलिए उन्होंने कहा कि यह संसार संख्यामय है।उनको तथा उनके शिष्यों को संख्याओं बहुत अधिक लगाव था।उनका विचार था कि लम्बाइयों को ठीक-ठीक मापा जा सकता है।परन्तु बाद में पता चला कि उनका विचार सही नहीं है।यह पता तब चला जब उन्हें ज्ञात हुआ कि अपरिमेय संख्याएं भी होती है जिन्हें ठीक-ठीक नहीं मापा जा सकता है।
प्रश्न:5.पाइथागोरस प्रमेय के लिए प्रमाण (Proof for Pythagoras Theorem),पाइथागोरस प्रमेय प्रमाण कक्षा 10 (Pythagoras Theorem Proof Class 10):
उत्तर-पाइथागोरस प्रमेय को प्राकृत संख्याओं के द्वारा आसानी से प्रमाणित किया जा सकता है।ऊपर बीजीय पद लेकर पाइथागोरस की प्रमेय को सिद्ध किया गया है।लेकिन यह मान अपरिमेय संख्याओं के रूप में प्राप्त होता है तो इससे ठीक-ठीक मापा नहीं जा सकता है जैसे –
\sqrt {1^2+1^2}=\sqrt 2
\sqrt 2=1.414213……. लेकिन यह सन्निकट मान ही कहलायेगा।दशमलव स्थानों को चाहे जितना आगे बढ़ा लें लेकिन हमे \sqrt 2 का सही-सही मान कभी भी प्राप्त नहीं हो सकता है।
इस खोज ने पाइथागोरस को सोचने पर मजबूर कर दिया। उसने जाना कि विश्व में ऐसी भी संख्याएं हैं जिन्हें परिमेय संख्याओं के रूप में व्यक्त नहीं किया जा सकता है।लेकिन उसने इस रहस्य को उजागर नहीं किया।
प्रश्न:6.बच्चों के लिए पाइथागोरस प्रमेय (Pythagoras Theorem for Kids):
उत्तर-यहाँ प्रमेय क्या कहता है:
किसी भी समकोण त्रिभुज में,उस वर्ग का क्षेत्रफल जिसकी भुजा कर्ण है (याद रखें कि यह समकोण की सम्मुख भुजा है) उन वर्गों के क्षेत्रफलों के योग के बराबर होता है जिनकी भुजाएँ दो अन्य भुजाएं होती हैं (दो भुजाएँ जो आपस में समकोण पर मिलती हैं)।
उपर्युक्त प्रश्नों के उत्तर द्वारा पाइथागोरस प्रमेय (Pythagoras Theorem),पाइथागोरस प्रमेय सूत्र (Pythagoras Theorem Formula) को ठीक से समझ सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |