Section Formula Class 10

Q: प्रश्न1.चतुर्थांश में निर्देशांकों के चिन्ह कैसे लेते हैं? (How Do You Take Sign of Co-ordinate in Quadrants?):

उत्तर:दोनों अक्षों XOX' और YOY' समतल को चार भागों में विभाजित करती है। इन्हें चतुर्थांश कहते हैं। XOY,YOX', X'OY' और Y'OX को क्रमशः प्रथम,द्वितीय,तृतीय और चतुर्थ चतुर्थांश कहते हैं।हम सदैव OX और OY दिशाओं को धनात्मक और OX',और OY' दिशाओं में ऋणात्मक लेते हैं। यदि समतल में किसी बिन्दु के निर्देशांक (x,y) हो तो प्रथम चतुर्थांश में x>0,y>0;(+,+) द्वितीय चतुर्थांश में x<0,y>0;(-,+) तृतीय चतुर्थांश में x<0,y<0;(-,-) चतुर्थ चतुर्थांश में x>0,y<0;(+,-)

Q: प्रश्न:2.कार्तीय निर्देशांक से क्या तात्पर्य है? (What is Meant by Cartesian Coordinate?):

उत्तर:माना किसी समतल में दो परस्पर लम्बवत् रेखाएँ XOX' और YOY' हैं जो कि बिन्दु O पर प्रतिच्छेद करती हैं।इन्हें निर्देशांक अक्ष (Coordinate Axes) कहते हैं और O को मूलबिन्दु (Origin) कहते हैं।XOX' और YOY' को समकोणिक अक्ष या आयतीय निर्देशांक अक्ष (Rectangular Axes) कहते हैं। अब समतल में बिन्दु P के निर्देशांक ज्ञात करने के लिए बिन्दु P से XOX' या x-अक्ष पर लम्ब PM और YOY' या y-अक्ष पर लम्ब PN डालते हैं।मूलबिन्दु O से M की दिष्ट दूरी (OM=x) बिन्दु P का x-निर्देशांक या भुज (abscissa) और M से P की दिष्ट दूरी (MP=y) बिन्दु जिसका भुज x और कोटि y हो बिन्दु (x,y) में निरूपित किए जाते हैं। अर्थात् बिन्दु के निर्देशांक लिखते समय x-निर्देशांक पहले और y-निर्देशांक बाद में लिखते हैं और इन्हें अल्प विराम (,) से अलग करते हुए छोटे कोष्ठक में लिखते हैं।

Q: प्रश्न:3.कार्तीय निर्देशांक की मुख्य बातें क्या हैं? (What are key Points of Cartesian Coordinate?):

उत्तर:(1.)किसी बिन्दु P के निर्देशांक (x,y) है तो इसे P\left(x_{1}, y_{1}\right) लिख सकते हैं। (2.)किसी बिन्दु का भुज, बिन्दु की y-अक्ष से लम्बवत् दूरी होती है। (3.)किसी बिन्दु की कोटि,बिन्दु की x-अक्ष से लम्बवत दूरी होती है। (4.)किसी बिन्दु का भुज y-अक्ष के दायीं ओर धनात्मक और बायीं ओर ऋणात्मक होता है। (5.)किसी बिन्दु की कोटि, x-अक्ष के ऊपर धनात्मक और नीचे ऋणात्मक होती है। (6.)यदि y=0 हो तो बिन्दु x-अक्ष पर स्थित होता है। (7.)यदि x=0 हो तो बिन्दु y-अक्ष पर स्थित होगा। उपर्युक्त प्रश्नों के द्वारा विभाजन सूत्र कक्षा 10 (Section Formula Class 10),अन्तः और बाह्य विभाजन सूत्र (Section Formula Internally and Externally)के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।

Mathematics Satyam June 24, 2022 10th Mathematics No Comments

Contents hide

1 1.विभाजन सूत्र कक्षा 10 (Section Formula Class 10),अन्तः और बाह्य विभाजन सूत्र (Section Formula Internally and Externally):

1.1 2.विभाजन सूत्र कक्षा 10 के साधित उदाहरण (Section Formula Class 10 Solved Examples):

1.2 3.विभाजन सूत्र कक्षा 10 की समस्याएं (Section Formula Class 10 Problems):

1.2.1 4.मुख्य बातें (HIGHLIGHTS):

1.2.2 5.विभाजन सूत्र कक्षा 10 (Section Formula Class 10),अन्तः और बाह्य विभाजन सूत्र (Section Formula Internally and Externally) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:

1.2.3 प्रश्न1.चतुर्थांश में निर्देशांकों के चिन्ह कैसे लेते हैं? (How Do You Take Sign of Co-ordinate in Quadrants?):

1.2.4 प्रश्न:2.कार्तीय निर्देशांक से क्या तात्पर्य है? (What is Meant by Cartesian Coordinate?):

1.2.5 प्रश्न:3.कार्तीय निर्देशांक की मुख्य बातें क्या हैं? (What are key Points of Cartesian Coordinate?):

1.2.5.1 Section Formula Class 10

2 विभाजन सूत्र कक्षा 10 (Section Formula Class 10)

2.1 Section Formula Class 10

1.विभाजन सूत्र कक्षा 10 (Section Formula Class 10),अन्तः और बाह्य विभाजन सूत्र (Section Formula Internally and Externally):

Section Formula Class 10

विभाजन सूत्र कक्षा 10 (Section Formula Class 10) का निर्देशांक ज्यामिति में अध्ययन किया जाता है।अन्तः और बाह्य विभाजन सूत्र की स्थापना निम्नलिखित है:
अन्तः विभाजन सूत्र (Section Formula Internally):

Section Formula Class 10

किन्हीं दो बिन्दुओं $A\left(x_{1}, y_{1}\right)$ और $B\left(x_{2}, y_{2}\right)$ पर विचार कीजिए और मान लीजिए बिन्दु P(x,y) रेखाखण्ड AB को $m_{1}: m_{2}$ के अनुपात में आंतरिक रूप से (Internally) विभाजित करता है।अर्थात्
है $\frac{P A}{P B}=\frac{m_{1}}{m_{2}}$ (देखिए आकृति)
x-अक्ष पर AR,PS और BT लम्ब खींचिए।x-अक्ष के समान्तर AQ और PC खींचिए।तब AA समरूपता कसौटी से:

$\triangle PAQ \sim \triangle BPC$
अतः $\frac{P A}{B P}=\frac{A Q}{P C}=\frac{P Q}{B C} \cdots(1)$
अब $AQ=RS=OS-OR=x-x_{1} \\ PC=ST=OT-OS=x_{2}-x \\ PQ=PS-QS=PS-AR=y-y_{1} \\ BC=BT-CT=BT-PS=y_{2}-y$
इन भागों को (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है:

$\frac{m_{1}}{m_{2}}=\frac{x-x_{1}}{x_{2}-x}=\frac{y-y_{1}}{y_{2}-y} \\ \frac{m_{1}}{m_{2}}=\frac{x-x_{1}}{x_{2}-x}$
लेने पर हमें $x=\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}$ प्राप्त होता है।
इसी प्रकार $\frac{m_{1}}{m_{2}}=\frac{y-y_{1}}{y_{2}-y}$ लेने पर हमें $y=\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}$ प्राप्त होता है।
अतः दो बिन्दुओं $A\left(x_{1}, y_{1}\right)$ और $B\left(x_{2}, y_{2}\right)$ को जोड़ने वाले रेखाखण्ड AB को के $m_{1}: m_{2}$ अनुपात में आन्तरिक रूप से विभाजित करनेवाले बिन्दु P(x,y) के निर्देशांक हैं:

$\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}},\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}$
उपर्युक्त को विभाजन सूत्र (Section Formula) कहते हैं।
विशिष्ट स्थिति:एक रेखाखण्ड का मध्यबिन्दु उसे 1:1 के अनुपात में विभाजित करता है।अतः बिन्दुओं $A\left(x_{1}, y_{1}\right)$ और $B\left(x_{2}, y_{2}\right)$ को जोड़ने वाले रेखाखण्ड AB के मध्यबिन्दु के निर्देशांक

$\left(\frac{1 \cdot x_{1}+1 \cdot x_{2}}{1+1}, \frac{1 \cdot y_{1}+1 \cdot y_{2}}{1+1}\right) =\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)$ होंगे।
बाह्य विभाजन सूत्र (Section Formula Externally):

Section Formula Class 10

माना समतल में स्थित बिन्दु $A\left(x_{1}, y_{1}\right)$ और $B\left(x_{2}, y_{2}\right)$ हैं।बिन्दु P(x,y) रेखाखण्ड AB को $m_{1}: m_{2}$ में बाह्य विभाजन करता है। बिन्दु A,B और P से x-अक्ष पर डाले गए लम्ब क्रमशः AL,BN और PM हैं।बिन्दु A से PM पर लम्ब AQ और B से BM पर लम्ब BR डाला।
तब $OL=x_{1}, ON=x_{2},OM=x, AL=y, B N=y_{2}$ और PM=y
$AQ=LM=OM-OL=x-x_{1} \\ B R=N M=O M-O N=x-x_{2} \\ P Q=PM-QM=PM-AL=y-y_{1}$ और $PR=PM-RM=PM-BN=y-y_{2}$
चित्र में त्रिभुज APQ और त्रिभुज BRP स्पष्टतः समरूप त्रिभुज हैं अर्थात् $\triangle AQP \sim \triangle BRP\\ \because \frac{AQ}{BP}=\frac{AQ}{B R}=\frac{P Q}{P R} \\ \Rightarrow \frac{m_{1}}{m_{2}} =\frac{x-x_{1}}{x-x_{2}}=\frac{y-y_{1}}{y-y_{2}}$
अब $\frac{m_{1}}{m_{2}}=\frac{x-x_{1}}{x-x_{2}} \\ \Rightarrow m_{1} x-m_{1} x_{2}=m_{2} x-m_{2} x_{1}\\ \Rightarrow \left(m_{1}-m_{2}\right) x=m_{1} x_{2}-m_{2} x_{1}\\ \therefore x=\frac{m_{1} x_{2}-m_{2} x_{1}}{m_{1}-m_{2}}$
पुनः $\frac{m_{1}}{m_{2}}=\frac{y-y_{1}}{y-y_{2}}\\ \Rightarrow m_{1} y-m_{1} y_{2}=m_{2} y-m_{2} y_{1}\\ \Rightarrow\left(m_{1}-m_{2}\right) y=m_{1} y_{2}-m_{2} y_{1}\\ \Rightarrow y=\frac{m_{1} y_{2}-m_{2} y_{1}}{m_{1}-m_{2}}$
अतः P बिन्दु के अभीष्ट निर्देशांक $\left(\frac{m_{1} x_{2}-m_{2} x_{1}}{m_{1}-m_{2}},\frac{m_{1} y_{2}-m_{2} y_{1}}{m_{1}-m_{2}}\right)$
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Find Distance in Coordinate Geometry

2.विभाजन सूत्र कक्षा 10 के साधित उदाहरण (Section Formula Class 10 Solved Examples):

Example:1.उस बिन्दु के निर्देशांक ज्ञात कीजिए जो बिन्दुओं (-1,7) और (4,-3) को मिलाने वाले रेखाखण्ड को 2:3 के अनुपात में विभाजित करता है।
Solution:माना अभीष्ट बिन्दु (x,y) है तब अन्तः विभाजन सूत्र से:

$x=\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}} \\ =\frac{2(4)+3(-1)}{2+3} \\ =\frac{+8-3}{5} \\ =\frac{5}{5}=1 \\ y =\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}} \\ =\frac{2 \times -3+3 \times 7}{2+3} \\ =\frac{-6+21}{5} \\ =\frac{15}{5}=3$
अतः अभीष्ट बिन्दु के निर्देशांक (1,3) है।
Example:2.बिन्दुओं (4,-1) और (-2,-3) को जोड़ने वाले रेखाखण्ड को समत्रिभाजित करनेवाले बिन्दुओं के निर्देशांक ज्ञात कीजिए।
Solution:माना अभीष्ट बिन्दु के निर्देशांक P(x,y) तथा Q(a,b) हैं।जब $m_{1} : m_{2}=1: 2$
तो $\left(x_{1}, y_{1}\right)=(4,-1),\left(x_{2}, y_{2}\right)=(-2,3) \\ x =\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}=\frac{1 \times -2+2(4)}{1+2} \\ =\frac{-2+8}{3}=\frac{6}{3}=2 \\ y =\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}=\frac{1 \times -3+2 \times -1}{1+2} \\ =\frac{-3-2}{3}=-\frac{5}{3}$
अभीष्ट बिन्दु P के निर्देशांक $(2,-\frac{5}{3}) \\ m_{1} : m_{2}=2: 1 \\ a=\frac{ m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}=\frac{2 \times -2+1 \times 4}{1+2} =\frac{-4+4}{3}=\frac{0}{3}=0 \\ b=\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}=\frac{2 \times -3+1 \times -1}{2+1} \\ =\frac{-6-1}{3}=-\frac{7}{3}$
अभीष्ट बिन्दु Q के निर्देशांक $(0,-\frac{7}{3})$
Example:3.आपके स्कूल में खेलकूद आयोजित करने के लिए,एक आयताकार मैदान ABCD में, चूने से परस्पर 1m की दूरी पर पंक्तियां बनाई गई हैं।AD के अनुदिश परस्पर 1m की दूरी पर 100 गमले रखे गए हैं जैसा कि आकृति में दर्शाया गया है।निहारिका दूसरी पंक्ति में AD के $\frac{1}{4}$ भाग के बराबर की दूरी दौड़ती है और वहाँ एक हरा झण्डा गाड़ देती है।प्रीत आठवीं पंक्ति में AD के $\frac{1}{5}$ भाग के बराबर की दूरी दौड़ती है और वहाँ एक लाल झण्डा गाड़ देती है।दोनों झंड़ों के बीच दूरी क्या है? यदि रश्मि को एक नीला झंडा इन दोनों झंडों को मिलाने वाले रेखाखण्ड पर ठीक आधी दूरी (बीच में) पर गाड़ना हो तो उसे अपना झण्डा कहाँ गाड़ना चाहिए।
Solution:भुजा AD पर 1मीटर की दूरी पर 100 गमले रखे हुए हैं।
AD=100 मीटर

Section Formula Class 10

निहारिका के झण्डे की स्थिति=दूसरी पंक्ति में AD के $\frac{1}{4}$ भाग के बराबर दूरी = $\frac{1}{4} \times 100=25$
हरे झण्डे के निर्देशांक (2,25) हैं।
प्रीत के झण्डे (लाल) की स्थिति=आठवीं पंक्ति में AD के $\frac{1}{5}$ भाग के बराबर दूरी = $\frac{1}{5} \times 100=20$
लाल झण्डे के निर्देशांक (8,20)
हरे झण्डे और लाल झण्डे के बीच की दूरी= $\sqrt{(8-2)^{2}+(20-25)^{2}} \\ =\sqrt{36+25}=\sqrt{61}$
रश्मि को इन दोनों झण्डों को मिलाने वाले रेखाखण्ड के मध्य-बिन्दु पर नीला झण्डा गाड़ना है तब मध्यबिन्दु के निर्देशांक

$\left(\frac{2+8}{2}, \frac{25+20}{2}\right) \\ =(5,\frac{45}{2})=(5,22.5)$
अतः रश्मि को पाँचवीं पंक्ति में AD के अनुदिश 22.5 मीटर की दूरी पर झण्डा गाड़ना चाहिए।
Example:4.बिन्दुओं (-3,10) और (6,-8) को जोड़ने वाले रेखाखण्ड को बिन्दु (-1,6) किस अनुपात में विभाजित करता है।
Solution:(x,y)=(-1,6)

$P\left(x_{1}, y_{1}\right)=(-3,10), Q\left(x_{2}, y_{2}\right)=(6,-8)$
माना अभीष्ट अनुपात $m_{1}:m_{2}$ है।

$x=\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}} \\ -1=\frac{m_{1}(6)+m_{2}(-3)}{m_{1}+m_{2}} \\ \Rightarrow -m_{1}-m_{2} =6 m_{1}-3 m_{2} \\ \Rightarrow-m_{1}-6 m_{1}=-3 m_{2}+m_{2} \\ \Rightarrow-7 m_{1}=-2 m_{2} \\ \Rightarrow m_{1} : m_{2}=2: 7$
Example:5.वह अनुपात ज्ञात कीजिए जिसमें बिन्दुओं A(1,-5) और B(-4,5) को मिलाने वाला रेखाखण्ड x-से विभाजित होता है।इस विभाजन बिन्दु के निर्देशांक भी ज्ञात कीजिए।
Solution:माना विभाजन बिन्दु के निर्देशांक (x,0)
तथा $A\left(x_{1}, y_{1}\right)=(1,-5), B=(-4,5) \\ y=\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}} \\ 0=\frac{m_{1}(5)+m_{2}(-5)}{m_{1}+m_{2}} \\ \Rightarrow 5 m_{1}-5 m_{2}=0 \\ \Rightarrow 5 m_{1}=5 m_{2} \Rightarrow m_{1}:m_{2}=1: 1 \\ x=\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}} \\ =\frac{1(-4)+1(1)}{1+1}=\frac{-4+1}{2} \\ =\frac{-3}{2}$
अतः अभीष्ट बिन्दु के निर्देशांक $(-\frac{3}{2},0)$
Example:6.यदि बिन्दु (1,2),(4,y),(x,6) और (3,5) इसी क्रम में लेने पर एक समान्तर चतुर्भुज के शीर्ष हो तो x और y ज्ञात कीजिए।
Solution:माना A(1,2),B(4,y),C(x,6) D(3,5)
समान्तर चतुर्भुज ABCD के विकर्ण AC और BD होंगे।ये परस्पर समद्विभाजित करते हैं
AC के मध्यबिन्दु के निर्देशांक = $\left(\frac{1+x}{2}, \frac{2+6}{2}\right) \\ =\left(\frac{1+x}{2}, 4\right)$
BD के मध्यबिन्दु के निर्देशांक = $\left(\frac{4+3}{2}, \frac{y+5}{2}\right) \\ =\left(\frac{7}{2}, \frac{y+5}{2}\right)$
AC और BD का मध्यबिन्दु समान होगा क्योंकि समान्तर चतुर्भुज ABCD के विकर्ण समद्विभाजित करते हैं।

$\frac{1+x}{2}=\frac{7}{2} \Rightarrow 1+x=7 \Rightarrow x=6 \\ \frac{y+5}{2}=4 \Rightarrow y+5=8 \Rightarrow y=3$
अतः $\Rightarrow x=6, y=3$

Example:7.बिन्दु A के निर्देशांक ज्ञात कीजिए जहाँ AB वृत्त का व्यास है जिसका केन्द्र (2,-3) है तथा B के निर्देशांक (1,4) हैं।
Solution:माना A के निर्देशांक है

Section Formula Class 10

तथा $B\left(x_{2}, y_{2}\right)=(1,4),(x, y)=(2,-3)\\ x=\frac{x_{1}+x_{2}}{2}\\ 2=\frac{x_{1}+1}{2} \Rightarrow x_{1}=4-1 \Rightarrow x_{1}=3\\ y=\frac{y_{1}+y_{2}}{2} \Rightarrow -3=\frac{y_{1}+4}{2}\\ \Rightarrow -3 \times 2=y_{1}+4 \Rightarrow y_{1}=-6-4\\ \Rightarrow y_{1}=-10$
अतः अभीष्ट बिन्दु A के निर्देशांक (3,-10) है।
Example:8.यदि A और B क्रमशः (-2,-2) और (2,-4) हो तो बिन्दु P के निर्देशांक ज्ञात कीजिए ताकि AP= $\frac{3}{7}$ AB हो और P रेखाखण्ड AB पर स्थित हो।
Solution:माना अभीष्ट बिन्दु P(x,y) है।

$AB=\frac{3}{7} A B\\ \Rightarrow \frac{A B}{A P}=\frac{7}{3} \\ \Rightarrow \frac{A B}{A P}-1=\frac{7}{3}-1\\ \Rightarrow \frac{A B-A P}{A P}=\frac{7-3}{3}\\ \Rightarrow \frac{B P}{A P}=\frac{4}{3}\\ \Rightarrow \frac{A P}{B P}=\frac{3}{4}\\ \Rightarrow A P: B P=m_{1} : m_{2}=3: 4$
माना $A\left(x_{1}, y_{1}\right)=(-2,-2)$ तथा $B\left(x_{2},y_{2}\right)=(2,-4)\\ x=\frac{m_{1} x_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\\ =\frac{3 \times 2+4 \times-2}{3+4}=\frac{6-8}{7} \\ x =\frac{-2}{7} \\ y =\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}} \\ =\frac{3 \times -4+4 \times -2}{3+4} \\ =\frac{-12-8}{5}=\frac{-20}{7}$
अतः बिन्दु P के निर्देशांक $(\frac{-2}{7},\frac{-20}{7})$
Example:9.बिन्दुओं A(-2,2) और B(2,8) को जोड़नेवाले रेखाखण्ड AB को चार बराबर भागों में विभाजित करनेवाले बिन्दुओं के निर्देशांक ज्ञात कीजिए।
Solution:माना AB बिन्दुओं C, D, E पर विभाजित होता है।
माना $A\left(x_{1}, y_{1}\right)=(-2,2), B\left(x_{2}, y_{2}\right)=(2,8)$
C बिन्दु के निर्देशांक के लिए $m_{1} : m_{2}=1 : 3 \\ x=\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}} \\ =\frac{1 \times 2+3 \times-2}{1+3} \\ =\frac{2-6}{4}=-\frac{4}{4} \\ \Rightarrow x=-1 \\ y=\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}} \\ =\frac{1 \times 8+3 \times 2}{1+3} \\ =\frac{8+6}{4}=\frac{14}{4}=\frac{7}{2}$
C बिन्दु के अभीष्ट निर्देशांक $(-1,\frac{7}{2})$
D बिन्दु के निर्देशांक के लिए $m_{1}: m_{2}=2: 2=1: 1$
अतः मध्यबिन्दु के निर्देशांक = $\left(\frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2}\right) \\ =\left(\frac{-2+2}{2}, \frac{2+8}{2}\right) \\ =\left(\frac{0}{2}, \frac{10}{2}\right) \\ =(0,5)$
D बिन्दु के अभीष्ट निर्देशांक (0,5)
E बिन्दु के निर्देशांक के लिए $m_{1} : m_{2}=3: 1 \\ x =\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}} \\ =\frac{3 \times 2+1 \times-2}{3+1} \\ =\frac{6-2}{4} \\=\frac{4}{4}=1 \\ y =\frac{m_{1} x_{2}+m_{2} y_{1}}{m_{1}+m_{2}} \\ =\frac{3 \times 8+1 \times 2}{3+1} \\ =\frac{24+2}{4} \\ =\frac{26}{4}= \frac{13}{2}$
E बिन्दु के अभीष्ट निर्देशांक $(1, \frac{13}{2})$ हैं।
अतः AB को चार भागों में विभाजित करनेवाले बिन्दुओं के निर्देशांक $\left(-1,\frac{7}{2}\right),(0,5),\left(1, \frac{13}{2}\right)$ हैं।
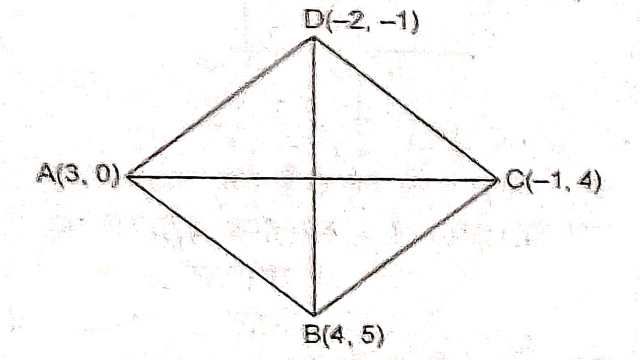
Example:10.एक समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष इसी क्रम में (3,0),(4,5),(-1,4) और (-2,-1) हैं।
Solution: माना समचतुर्भुज ABCD के विकर्ण AC तथा BD है।
A(3,0),B(4,5),C(-1,4),D(-2,-1)

Section Formula Class 10

AC= $\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\\ =\sqrt{(-1-3)^{2}+(4-6)^{2}}\\ =\sqrt{(-4)^{2}+16} \\ =\sqrt{16+16} \\ =\sqrt{32}=4 \sqrt{2}\\ BD=\sqrt{(-2-4)^{2}+(-1-5)^{2}} \\ =\sqrt{(-6)^{2}+(-6)^{2}} \\ =\sqrt{36+36}=\sqrt{72}=6 \sqrt{2}$
समचतुर्भुज ABCD का क्षेत्रफल= $\frac{1}{2}$ × विकर्णों का गुणनफल
= $\frac{1}{2} \times 4 \sqrt{2} \times 6 \sqrt{2}$ =24 वर्ग इकाई
उपर्युक्त उदाहरणों के द्वारा विभाजन सूत्र कक्षा 10 (Section Formula Class 10),अन्तः और बाह्य विभाजन सूत्र (Section Formula Internally and Externally) को समझ सकते हैं।

3.विभाजन सूत्र कक्षा 10 की समस्याएं (Section Formula Class 10 Problems):

Section Formula Class 10

(1.)बिन्दुओं (2,-3) और (5,6) को मिलाने वाली रेखाखण्ड y-अक्ष को किस अनुपात में विभाजित होता है।
(2.)ज्ञात कीजिए कि रेखा 3x+y=9 बिन्दुओं (1,3) और (2,7) को मिलनेवाले रेखाखण्ड को किस अनुपात में विभाजित करती है।
(3.)वह अनुपात ज्ञात कीजिए जबकि बिन्दु (-3,p) बिन्दुओं (-5,-4) और (-2,3) को अन्तः विभाजित करता है। p का मान ज्ञात कीजिए।
उत्तर (Answers):(1.) 2:5 बाह्य विभाजन
(2.)3:4
(3.)2:1, p= $\frac{2}{3}$
उपर्युक्त सवालों को हल करने पर विभाजन सूत्र कक्षा 10 (Section Formula Class 10),अन्तः और बाह्य विभाजन सूत्र (Section Formula Internally and Externally) को ठीक से समझ सकते हैं।

Also Read This Article:-Basic Proportionality Theorem Class 10

4.मुख्य बातें (HIGHLIGHTS):

(1.)अन्तः विभाजन सूत्र से बाह्य विभाजन सूत्र प्राप्त करने के लिए $m_{1}$ या $m_{2}$ का चिन्ह ऋण कर देते हैं।
(2.)यदि बाह्य विभाजन में $|m_{1}|>|m_{2}|$ हो तो विभाजन बिन्दु B के दायीं ओर (रेखा AB को B की ओर बढ़ाने पर) प्राप्त होता है।इसी प्रकार $|m_{1}|<|m_{2}|$ हो तो विभाजन बिन्दु A के बायीं ओर (रेखा AB को A की ओर बढ़ाने पर) प्राप्त होता है।
(3.)यदि बिन्दु P(x,y) रेखाखण्ड को $\lambda : 1$ में विभाजित करता है तो p के निर्देशांक $\left(\frac{x_{1}+\lambda x_{2}}{1+\lambda}, \frac{y_{1}+\lambda y_{2}}{1+\lambda}\right)$ होते हैं। $\lambda$ को प्राचल मानते हुए बिन्दु $\left(x_{1}, y_{1}\right)$ व $\left(x_{2}, y_{2}\right)$ मिलाने वाली रेखा पर किसी बिन्दु के निर्देशांक को उपयुक्त रूप में व्यक्त कर सकते हैं।

5.विभाजन सूत्र कक्षा 10 (Section Formula Class 10),अन्तः और बाह्य विभाजन सूत्र (Section Formula Internally and Externally) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:

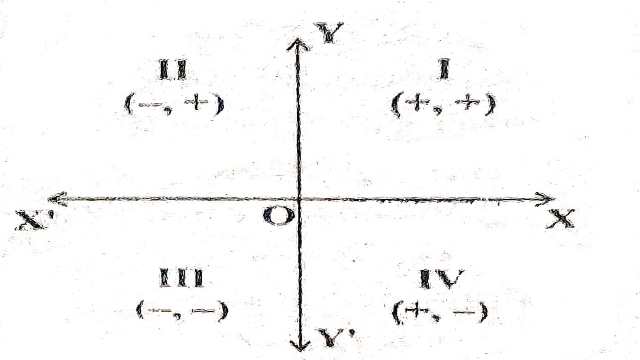
Section Formula Class 10

प्रश्न1.चतुर्थांश में निर्देशांकों के चिन्ह कैसे लेते हैं? (How Do You Take Sign of Co-ordinate in Quadrants?):

उत्तर:दोनों अक्षों XOX’ और YOY’ समतल को चार भागों में विभाजित करती है। इन्हें चतुर्थांश कहते हैं। XOY,YOX’, X’OY’ और Y’OX को क्रमशः प्रथम,द्वितीय,तृतीय और चतुर्थ चतुर्थांश कहते हैं।हम सदैव OX और OY दिशाओं को धनात्मक और OX’,और OY’ दिशाओं में ऋणात्मक लेते हैं।
यदि समतल में किसी बिन्दु के निर्देशांक (x,y) हो तो
प्रथम चतुर्थांश में x>0,y>0;(+,+)
द्वितीय चतुर्थांश में x<0,y>0;(-,+)
तृतीय चतुर्थांश में x<0,y<0;(-,-)
चतुर्थ चतुर्थांश में x>0,y<0;(+,-)

प्रश्न:2.कार्तीय निर्देशांक से क्या तात्पर्य है? (What is Meant by Cartesian Coordinate?):

उत्तर:माना किसी समतल में दो परस्पर लम्बवत् रेखाएँ XOX’ और YOY’ हैं जो कि बिन्दु O पर प्रतिच्छेद करती हैं।इन्हें निर्देशांक अक्ष (Coordinate Axes) कहते हैं और O को मूलबिन्दु (Origin) कहते हैं।XOX’ और YOY’ को समकोणिक अक्ष या आयतीय निर्देशांक अक्ष (Rectangular Axes) कहते हैं।
अब समतल में बिन्दु P के निर्देशांक ज्ञात करने के लिए बिन्दु P से XOX’ या x-अक्ष पर लम्ब PM और YOY’ या y-अक्ष पर लम्ब PN डालते हैं।मूलबिन्दु O से M की दिष्ट दूरी (OM=x) बिन्दु P का x-निर्देशांक या भुज (abscissa) और M से P की दिष्ट दूरी (MP=y) बिन्दु जिसका भुज x और कोटि y हो बिन्दु (x,y) में निरूपित किए जाते हैं। अर्थात् बिन्दु के निर्देशांक लिखते समय x-निर्देशांक पहले और y-निर्देशांक बाद में लिखते हैं और इन्हें अल्प विराम (,) से अलग करते हुए छोटे कोष्ठक में लिखते हैं।

प्रश्न:3.कार्तीय निर्देशांक की मुख्य बातें क्या हैं? (What are key Points of Cartesian Coordinate?):

उत्तर:(1.)किसी बिन्दु P के निर्देशांक (x,y) है तो इसे $P\left(x_{1}, y_{1}\right)$ लिख सकते हैं।
(2.)किसी बिन्दु का भुज, बिन्दु की y-अक्ष से लम्बवत् दूरी होती है।
(3.)किसी बिन्दु की कोटि,बिन्दु की x-अक्ष से लम्बवत दूरी होती है।
(4.)किसी बिन्दु का भुज y-अक्ष के दायीं ओर धनात्मक और बायीं ओर ऋणात्मक होता है।
(5.)किसी बिन्दु की कोटि, x-अक्ष के ऊपर धनात्मक और नीचे ऋणात्मक होती है।
(6.)यदि y=0 हो तो बिन्दु x-अक्ष पर स्थित होता है।
(7.)यदि x=0 हो तो बिन्दु y-अक्ष पर स्थित होगा।
उपर्युक्त प्रश्नों के द्वारा विभाजन सूत्र कक्षा 10 (Section Formula Class 10),अन्तः और बाह्य विभाजन सूत्र (Section Formula Internally and Externally)के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here
6.	Twitter	click here

Section Formula Class 10

विभाजन सूत्र कक्षा 10
(Section Formula Class 10)