Proofs in Mathematics
1.गणित में उपपत्तियाँ (Proofs in Mathematics),गणित में उपपत्तियाँ कक्षा 12 (Proofs in Mathematics Class 12):
गणित में उपपत्तियाँ (Proofs in Mathematics) के इस आर्टिकल में गणितीय साध्यों को सिद्ध (प्रमाणित) करने की विभिन्न विधियों के बारे में अध्ययन करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Continuity Class 12th
2.उपपत्ति क्या है? (What is a Proof?):
किसी गणितीय कथन की उपपत्ति में कथनों का एक अनुक्रम अंतर्विष्ट होता है,जिसके प्रत्येक कथन के औचित्य को किसी परिभाषित पद या किसी अभिगृहीत या किसी ऐसी साध्य द्वारा प्रमाणित करते हैं,जिसे निगमनिक विधि तथा कुछ अपरिभाषित पदों द्वारा केवल स्वीकार्य तार्किक नियमों का प्रयोग करके पूर्व प्रतिपादित किया जा चुका हो।
इस प्रकार प्रत्येक उपपत्ति निगमनिक तर्कों की एक श्रृंखला होती है,जिनमें से प्रत्येक की अपनी परिकल्पनाएँ तथा निष्कर्ष होते हैं।अधिकतर हम किसी साध्य को उसमें दिए हुए तथ्यों से प्रत्यक्ष रीति द्वारा सिद्ध करते हैं।परन्तु कभी-कभी साध्य को सीधे सिद्ध करने की दो विधियाँ प्रदर्शित होती हैं,नामतः प्रत्यक्ष उपपत्ति अथवा अप्रत्यक्ष उपपत्ति तथा इसके अतिरिक्त प्रत्येक विधि में तीन भिन्न-भिन्न तरीके होते हैं,जिनकी चर्चा नीचे की गई है।
3.प्रत्यक्ष उपपत्ति (Direct Proof):
यह साध्य की वह उपपत्ति है,जिसे हम सीधे रूप में प्रदत्त तथ्यों से प्रारम्भ कर साध्य की उपपत्ति स्थापित करते हैं।
(1.)सीधा-सीधा उपगमन (Approach):
यह तर्कों की एक श्रृंखला है,जो प्रदत्त अथवा कल्पित तथ्यों से सीधे प्रारम्भ करके,अभिगृहीतों,परिभाषित पदों तथा पूर्व प्रमाणित साध्यों की सहायता से तर्क के नियमों के प्रयोग द्वारा,सिद्ध किए जाने वाले निष्कर्ष को प्रमाणित करती है।
निम्नलिखित उदाहरण पर विचार कीजिए:
उदाहरण:1.यदि x^2-5 x+6=0 तो x=3 या x=2 है।
हल: x^2-5 x+6=0(दिया है )
\Rightarrow (x-3)(x-2)=0 (एक व्यंजक को तुल्य व्यंजक से बदलने पर)
\Rightarrow x-3=0 या x-2= (पूर्वप्रमाणित साध्य ab=0 तब a=0 या b=0 , a, b \in R)
\Rightarrow x-3+3=0+3 या x-2+2=0+2 (समीकरण के दोनों पक्षों में समान संख्या जोड़ने से उसकी प्रकृति परिवर्तित नहीं होती है।)
\Rightarrow x+0=3 या x+0=2 (योग के अन्तर्गत पूर्णांक के तत्समक (Identity) गुण के प्रयोग द्वारा)
\Rightarrow x=3 या x=2 (योग के अन्तर्गत पूर्णांक के तत्समक गुण के प्रयोग द्वारा।)
x^2-5 x+6=0 \Rightarrow x=3 या x=2
यहाँ p प्रदत्त कथन “x^2-5 x+6=0” है और q निष्कर्ष कथन “x=3 या x=2” है।
कथन p के व्यंजक x^2-5 x+6=0 को,इसके तुल्य एक अन्य व्यंजक (x-3)(x-2) से प्रतिस्थापित करके हम एक व्यंजक r:”(x-3)(x-2)=0″ प्राप्त करते हैं
यहाँ दो प्रश्न उठते हैं:
(i)व्यंजक (x-3)(x-2) किस प्रकार x^2-5 x+6=0 व्यंजक के समान (तुल्य) है?
(ii)किसी व्यंजक को उसके समान एक अन्य व्यंजक से हम कैसे प्रतिस्थापित कर सकते हैं? इनमें से प्रथम को गुणनखण्ड द्वारा सिद्ध कर चुके हैं अर्थात्
x^2-5 x+6=x^2-3 x-2 x+6=x(x-3)-2(x-3)= (x-3)(x-2)
द्वितीय प्रश्न तर्क के वैध रूप (तर्क के नियमों) द्वारा सम्भव होता है।
इसके उपरान्त r पूर्वकथन (premise) या प्रदत्त कथन हो जाता है,जिसमें कथन s:”x-3=0 या x-2=0″ प्राप्त होता है।प्रत्येक चरण (steps) का औचित्य कोष्ठक (brackets) में दिया है।
यह प्रक्रिया निरन्तर तब तक चलती रहती है जब तक हम अन्तिम निष्कर्ष पर नहीं पहुँच जाते हैं।
तर्क की प्रतीकात्मक समतुल्यता निगमन द्वारा यह प्रमाणित करने में है कि p \Rightarrow q सत्य है।
p से प्रारम्भ करके निगमन द्वारा p \Rightarrow r \Rightarrow s \Rightarrow q को प्रमाणित कीजिए।अतः “p \Rightarrow q” सत्य है।
उदाहरण:2.सिद्ध कीजिए की फलन f: R \rightarrow R जो f(x)=2x+5 द्वारा परिभाषित है,एक एकैकी (one-one) फलन है
उपपत्ति (Proof):ध्यान दीजिए कि फलन f एकैकी होगा यदि f\left(x_1\right)=f\left(x_2\right) \Rightarrow x_1=x_2
(एकैकी फलन की परिभाषा)
अब मान लीजिए कि f\left(x_1\right)=f\left(x_2\right) अर्थात्
2 x_1+5=2 x_2+5 \\ \Rightarrow 2 x_1+5-5=2 x_2+5-5 (दोनों पक्षों में समान संख्या जोड़ने से)
\Rightarrow 2 x_1+0=2 x_2+0 \\ \Rightarrow 2 x_1=2 x_2 (वास्तविक संख्याओं में योज्य तत्समक का गुण)
\Rightarrow \frac{2}{2} x_1=\frac{2}{2} x_2 (दोनों पक्षों को समान शून्येतर संख्या से विभाजित करने से)
\Rightarrow x_1=x_2
अतः फलन एकैकी है।
(2.)गणितीय आगमन (Methematical Induction) :
गणितीय आगमन,साध्यों को सिद्ध करने की एक ऐसी विधि है,जिसका स्वरूप निगमनिक होता है।इस विधि में उपपत्ति पूर्णरूपेण निम्नलिखित अभिगृहीत पर आधारित होती है।
N के एक प्रदत्त उपसमुच्चय S में,यदि
(i)प्राकृत संख्या 1 \in S तथा
(ii)प्राकृत संख्या K+1 \in S जब कभी, k \in S तो S=N
गणितीय आगमन का सिद्धान्त यह है कि यदि एक कथन “S(n),n=1 के लिए सत्य है” (अथवा किसी अन्य प्रारम्भिक संख्या j के लिए सत्य है) और यदि कथन n=k के लिए सत्य होने में यह अंतर्निहित है कि वह n=k+1 के लिए अनिवार्यतः सत्य है (जब कभी धन पूर्णांक k \geq j ), तो प्रदत्त कथन किसी भी धन पूर्णांक n, जहाँ k \geq j के लिए सत्य होता है।
अब हम कुछ उदाहरण लेते हैं।
उदाहरण:3.यदि A=\left[\begin{array}{cc}\cos \theta \sin \theta \\ -\sin \theta \cos \theta \end{array}\right], तो दिखाइए कि A^n=\left[\begin{array}{ll}\cos n \theta & \sin n \theta \\ -\sin n \theta & \cos n \theta\end{array}\right]
हल:मान लिया कि P(n): A^n=\left[\begin{array}{ll}\cos n \theta & \sin n \theta \\ -\sin n \theta & \cos n \theta\end{array}\right]
हम देखते हैं कि P(1) : A^{\prime}=\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta\end{array}\right]
अतः P(1) सत्य है।
अब मान लिया कि P(k) सत्य है,अर्थात्
P(k) : A^k=\left[\begin{array}{cc} \cos k \theta & \sin k \theta \\ -\sin k \theta & \cos k \theta \end{array}\right]
तो हम सिद्ध करना चाहते हैं कि P(k+1) सत्य है,जब कभी P(k) सत्य है,अर्थात् P(k+1): A^{k+1}= \left[\begin{array}{cc} \cos (k+1) \theta & \sin (k+1) \theta \\ -\sin (k+1) \theta & \cos (k+1) \theta \end{array}\right]
सत्य है
पुनः A^{k+1}=A^k \cdot A
चूँकि P(k) सत्य है,इसलिए
A^{k+1}=\left[\begin{array}{cc} \cos k \theta & \sin k \theta \\ -\sin k \theta & \cos k \theta \end{array}\right] \left[\begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right] \\ A^{k+1}=\left[\begin{array}{cc} \cos k \theta & \sin k \theta \\ -\sin k \theta & \cos k \theta \end{array}\right]\left[\begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right] \\ =\left[\begin{array}{cc} \cos k \theta \cdot \cos \theta-\sin k \theta \cdot \sin \theta & \cos k \theta \sin \theta+\sin k \theta \cos \theta \\ -\sin k \theta \cos \theta-\cos k \theta \sin \theta &-\sin k \theta \sin \theta+\cos k \theta \cos \theta \end{array}\right] (आव्यूह गुणन द्वारा)
=\left[\begin{array}{cc} \cos (k+1) \theta & \sin (k+1) \theta \\ -\sin (k+1) \theta & \cos (k+1) \theta \end{array}\right]
अतः P(k+1) सत्य है,जब कभी P(k) सत्य है।
अतएव P(n), n के सभी मानों (धन पूर्णांक) के लिए सत्य है।
(3.)विभिन्न स्थितियों में विखण्डन द्वारा अथवा निःशेषण द्वारा उपपत्ति
कथन को सिद्ध करने की यह विधि केवल तभी सम्भव है,जब p को अनेक कथनों r,s,t (मान लिया) में विखण्डित किया जा सकता हो जैसा कि p=r \vee s \vee t (जहाँ प्रतीक है “या” के लिए)
यदि सप्रतिबन्ध कथनों r \Rightarrow q ;
s \Rightarrow q; तथा t \Rightarrow q
को प्रमाणित किया जाए,तो (r \vee s \vee t) \Rightarrow q ,सिद्ध हो जाता है और इस प्रकार p \Rightarrow q प्रमाणित होता है।
इस विधि में परिकल्पना की प्रत्येक सम्भव दशा को जाँचा जाता है।यह विधि व्यावहारिक रूप से केवल तभी सुविधाजनक है जब विखण्डन द्वारा प्राप्त कथनों की संख्या कम हो।
उदाहरण:4.किसी \triangle ABC, में सिद्ध कीजिए कि a=b \cos C+c \cos B
हल:मान लीजिए कि p कथन “ABC एक त्रिभुज है” तथा q कथन a=b \cos C+c \cos B
है
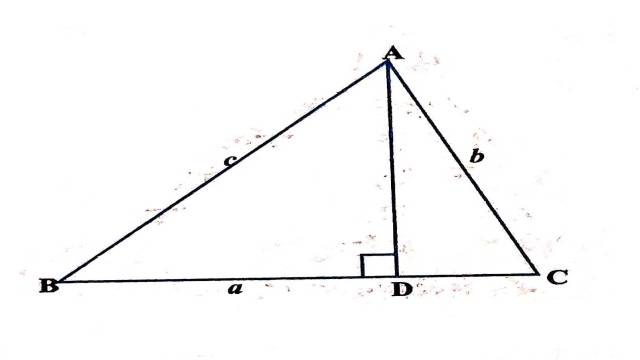
मान लीजिए कि ABC एक त्रिभुज है।शीर्ष A से BC (आवश्यकतानुसार बढ़ाई गई) पर लम्ब AD खींचिए।
हमें ज्ञात है कि एक त्रिभुज या तो न्यूनकोण त्रिभुज या अधिककोण त्रिभुज या समकोण त्रिभुज होता है,इसलिए हम p को r,s तथा t में विखण्डित कर सकते हैं,जहाँ
r:ABC एक न्यूनकोण त्रिभुज है,जिसमें न्यूनकोण है।
s:ABC एक अधिककोण त्रिभुज है,जिसमें अधिककोण है।
t:ABC एक समकोण त्रिभुज है,जिसमें समकोण है।
अतः हम साध्य को उपर्युक्त तीनों सम्भावनाओं के लिए अलग-अलग सिद्ध करते हैं।
दशा (i)जब \angle A, \angle B तथा \angle C तीनों ही न्यूनकोण हैं
समकोण \triangle ADB,द्वारा
\frac{B D}{A B}=\cos B
अर्थात् BD=AB \cos B=c \cos B
समकोण \triangle A D C द्वारा
\frac{C D}{A C}=\cos C
अर्थात् C D=A C \cos C
अब a=BD+CD \\ \Rightarrow a=c \cos B+b \cos C \cdots(1)
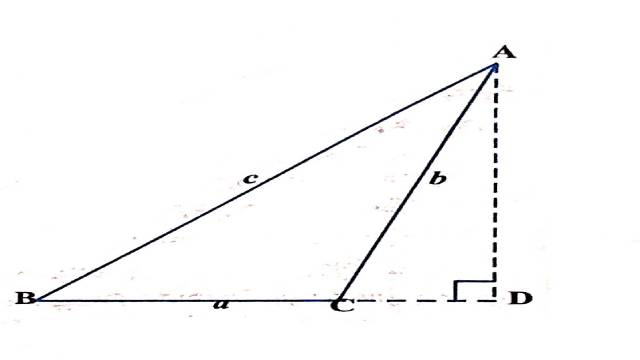
दशा (ii)जब \angle C अधिक कोण है
समकोण \triangle ADB द्वारा
\frac{B D}{A B}=\cos B
अर्थात् BD=AB \cos B \\ =C \cos B
समकोण \triangle A D C द्वारा
\frac{C D}{A C} =\cos \angle A C D \\ =\cos (180-C) \\ =-\cos C
अर्थात् CD =-A C \cos C \\ =-b \cos C
अब a=B C=B D-C D
अर्थात् a =c \cos B-(-b \cos C) \\ a=c \cos B+b \cos C \quad \cdots(2)
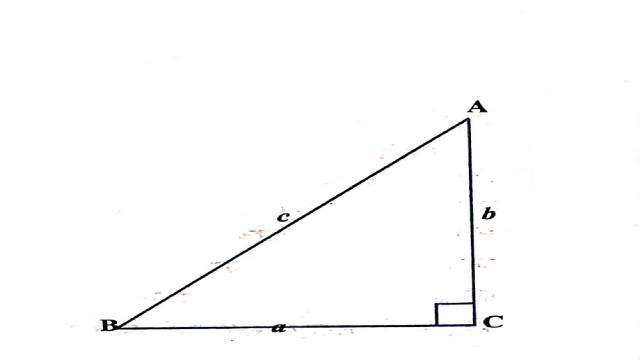
दशा (iii)जब \angle C समकोण है
\triangle A C B द्वारा
\frac{B C}{A B}=\cos B
अर्थात् B C=A B \cos B
तथा a=c \cos B \\ b \cos C=b \cos 90^{\circ}=0
अतः हम लिख सकते हैं a=0+c \cos \beta \\ =b \cos C+c \cos B \\ \Rightarrow a=b \cos C+r \cos B \cdots(3)
समीकरण (1),(2) तथा (3) से हम पाते हैं, कि में a=b \cos C+c \cos B
दशा (i) r \Rightarrow q प्रमाणित है।
दशा (ii) s \Rightarrow q प्रमाणित है।
तथा दशा (iii) t \Rightarrow q प्रमाणित है।
अतः r \vee s \vee t \Rightarrow q प्रमाणित है अर्थात् p \Rightarrow q प्रमाणित है,
4.अप्रत्यक्ष उपपत्ति (Indirect Proof):
दिए गए साध्य को सीधे प्रमाणित करने के एवज में,हम उसके समतुल्य किसी साध्य को सिद्ध करके,प्रदत्त साध्य को प्रमाणित करते हैं
(1.)विरोधोक्ति द्वारा उपपत्ति (Reductio Ad Absurdum):
यहाँ हम इस मान्यता से प्रारम्भ करते हैं कि परिकल्पना सत्य है तथा निष्कर्ष असत्य है।तर्क के नियमों के प्रयोग द्वारा हम इस निष्कर्ष पर पहुँचते है कि एक ज्ञात सत्य कथन,असत्य है,जो एक विरोधोक्ति है।अतः प्रदत्त कथन सत्य है इस विधि को एक उदाहरण द्वारा समझते हैं।
उदाहरण:5.सभी अभाज्य संख्याओं का समुच्चय अपरिमित (Infinite) होता है ।
हल:मान लीजिए कि समस्त अभाज्य संख्याओं (Prime Numbers) का समुच्चय P है जो अपरिमित है।हम इस कथन के निषेध (Negation) को,अर्थात् समस्त अभाज्य संख्याओं का समुच्चय अपरिमित नहीं है, सत्य मान लेते हैं,अर्थात् समस्त अभाज्य संख्याओं का समुच्चय परिमित है।इसलिए हम समस्त अभाज्य संख्याओं को सूचीबद्ध कर सकते हैं।मान लीजिए P_1, P_2, P_3, \cdots, P_k कि समस्त अभाज्य संख्याओं की सूची है।अब मान लीजिए
N=\left(P_1 P_2 P_3 \ldots P_k\right)+1 \ldots(1)
स्पष्ट है कि N अभाज्य संख्याओं की सूची में नहीं है,क्योंकि यह सूची की किसी भी संख्या से अधिक है।
N या तो अभाज्य है या संयुक्त संख्या है।
यदि N अभाज्य है तो (1) से स्पष्ट होता है कि एक ऐसी अभाज्य संख्या का अस्तित्व है,जो सूची में नहीं है।
दूसरी ओर,यदि N एक संयुक्त संख्या है,तो इसका कम से कम एक अभाज्य भाजक (Divisor) होना चाहिए।परन्तु सूची की कोई भी संख्या N को विभाजित (पूर्णरूप से) नहीं कर सकती है,क्योंकि उनमें से किसी के द्वारा N को विभाजित करने पर शेषफल सदैव 1 बचता है।अतः N का अभाज्य भाजक सूची के अतिरिक्त कोई अन्य संख्या है।
किन्तु यह,इस कथन का कि हमने सभी अभाज्य संख्याओं की सूची बना ली है,विरोधोक्ति है।
इस प्रकार हमारी पूर्वधारणा कि सभी अभाज्य संख्याओं का समुच्चय परिमित है,असत्य है।
अतः सभी अभाज्य संख्याओं का समुच्चय अपरिमित होता है।
(2.)प्रदत्त कथन का प्रतिधनात्मक (contrapositive) कथन के प्रयोग द्वारा उपपत्ति:
यहाँ सप्रतिबन्ध कथन P \Rightarrow q को सिद्ध करने के स्थान पर हम उसके समतुल्य कथन \sim q \Rightarrow \sim p को सिद्ध करते हैं।
किसी दिए हुए सप्रतिबन्ध कथन के निष्कर्ष तथा परिकल्पना का विनिमय करके उनमें से प्रत्येक का निषेधन करने से प्रदत्त कथन का प्रतिधनात्मक कथन बनता है।
उदाहरण:6.सिद्ध कीजिए कि f(x)=2x+5 द्वारा परिभाषित फलन f: R \rightarrow R एकैकी फलन है।
हल:फलन एकैकी होता है,यदि f\left(x_1\right)=f\left(x_2\right) \\ \Rightarrow x_1=x_2
इसका प्रयोग करके हमें प्रमाणित करना है कि "2 x_1+5=2 x_2+5" \\ \Rightarrow " x_1=x_2" यह P \Rightarrow q , के रूप का है,जहाँ 2 x_1+5=2 x_2+5 कथन p है तथा x_1=x_2 कथन q है।इस बात को हम उदाहरण 2 में “प्रत्यक्ष विधि” द्वारा सिद्ध कर चुके हैं।
हम इसे प्रदत्त कथन के प्रतिधनात्मक कथन के प्रयोग द्वारा भी प्रमाणित कर सकते हैं।दिए गए कथन का प्रतिधनात्मक कथन \sim q \Rightarrow \sim p है,अर्थात् “यदि f(x_1)=f(x_2) तो x_1=x_2” का प्रतिधनात्मक है “यदि x_1 \neq x_2 तो f(x_1) \neq f(x_2)“
अब x_1 \neq x_2 \\ \Rightarrow 2 x_1 \neq 2 x_2 \\ \Rightarrow 2 x_1+5 \neq 2 x_2+5 \\ \Rightarrow f\left(x_1\right) \neq f\left(x_2\right)
क्योंकि ” \sim q \Rightarrow \sim p” और ” p \Rightarrow q ” समतुल्य है,इस प्रकार उपपत्ति पूर्ण है।
उदाहरण:7.प्रमाणित कीजिए कि “यदि आव्यूह A, Invertible है,तो A, Non-singular है”
हल:उपर्युक्त कथन को प्रतीकात्मक रूप में लिखने पर p \Rightarrow q जहाँ p कथन “आव्यूह A, invertible है” तथा q कथन “A, non-singular है।”
प्रदत्त कथन को प्रमाणित करने के एवज में हम इसके प्रतिधनात्मक कथन को प्रमाणित करते हैं,अर्थात् यदि A एक non-singular आव्यूह नहीं है तो इसका अर्थ हुआ |A|=0 है।
अब A^{-1}=\frac{\operatorname{adj} A}{|A|} का अस्तित्व नहीं है,क्योंकि |A|=0
अतः A,Invertible नहीं है।
इस प्रकार हमने यह प्रमाणित कर दिया कि यदि A एक non-singular आव्यूह नहीं है तो A, invertible नहीं है।अर्थात्
\sim q \Rightarrow -p
अतः यदि एक आव्यूह A, invertible है,तो A, non-singular है।
(3.)प्रत्युदाहरण (Counter Example):
गणित के इतिहास में ऐसे अवसर भी आते हैं,जब किसी परिकल्पित व्यापकीकरण की वैध उपपत्ति ज्ञात करने के सभी प्रयास असफल हो जाते हैं और व्यापकीकरण के सत्यापन की अनिश्चितता अनिर्णित बनी रहती है।
ऐसी स्थिति में यह लाभप्रद है कि,कथन को असत्य सिद्ध करने के लिए,हम एक उदाहरण ढूँढ सकें।किसी कथन को अमान्य करने वाला उदाहरण प्रत्युदाहरण कहलाता है।
क्योंकि साध्य p \Rightarrow q का खण्डन,साध्य \sim(p \Rightarrow q) की केवल मात्र एक उपपत्ति होता है।अतः यह भी उपपत्ति की एक विधि है।
उदाहरण:8.कथन : प्रत्येक x \in N,\left(2^{2^n}+1\right) एक अभाज्य संख्या है।
यह कथन निम्न प्रेक्षणों के आधार पर एक समय सत्य समझा गया था:
2^{2^1}+1=2^2+1=5 जो कि एक अभाज्य संख्या है।
2^{2^2}+1=2^4+1=17 जो कि एक अभाज्य संख्या है।
2^{2^3}+1=2^8+1=257 जो कि एक अभाज्य संख्या है।
यद्यपि प्रथम दृष्टि में यह व्यापकीकरण सही प्रतीत होता है।अंततोगत्वा यह प्रतिपादित किया गया कि 2^{2^5}+1=2^{32}+1=4294967297 एक अभाज्य संख्या नहीं है क्योंकि 4294967297=641×6700417 है।जो दो संख्याओं का गुणनफल है (1 तथा स्वयं के अतिरिक्त) इस प्रकार यह व्यापकीकरण कि “प्रत्येक n के लिए 2^{2^n}+1 एक अभाज्य संख्या है \forall n \in N” असत्य है।
मात्र केवल यह एक उदाहरण कि अभाज्य संख्या नहीं है,का व्यापकीकरण को खण्डित करने के लिए पर्याप्त है।
अतः हमने सिद्ध कर दिया कि कथन “प्रत्येक n \in N के लिए, 2^{2^n}+1 एक अभाज्य संख्या है” सत्य नहीं है।
उदाहरण:9.कथन “प्रत्येक संतत फलन अवकलनीय होता है।” पर विचार कीजिए।
उपपत्ति:हम निम्नलिखित फलनों पर विचार करते हैं:
(i) f(x)=x^2
(ii) g(x)=e^x
(iii)-h(x)=\sin x
ये सभी फलन x के सभी मानों के लिए संतत है।यदि हम अवकलनीयता पर विचार करें तो ये x के सभी मानों के लिए अवकलनीय है।यह हमें इस विश्वास के लिए प्रेरित करता है कि कथन “प्रत्येक संतत फलन अवकलनीय होता है” सत्य है।किन्तु यदि हम फलन “\phi(x)=|x|” की अवकलनीयता की जाँच करें,जो कि संतत है,तो हम देखते हैं कि यह x=0 पर अवकलनीय नहीं है।इसका तात्पर्य यह हुआ कि कथन “प्रत्येक संतत फलन अवकलनीय होता है” असत्य है।फलन का केवल यह एक उदाहरण,व्यापकीकरण का खण्डन करने के लिए पर्याप्त है।अतः फलन को “\phi(x)=|x|” दिए गए कथन अर्थात् “प्रत्येक संतत फलन अवकलनीय होता है।” के खण्डन का प्रत्युदाहरण कहते हैं।
उपर्युक्त आर्टिकल में गणित में उपपत्तियाँ (Proofs in Mathematics),गणित में उपपत्तियाँ कक्षा 12 (Proofs in Mathematics Class 12) के बारे में बताया गया है।
Also Read This Article:- Continuity in Class 12
5.गणित में उपपत्तियाँ (Frequently Asked Questions Related to Proofs in Mathematics),गणित में उपपत्तियाँ कक्षा 12 (Proofs in Mathematics Class 12) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.आगमन तर्क से क्या तात्पर्य है? (What is Meant by Inductive Logic?):
उत्तर:आगमन हमारे अनुमान की वास्तविक सत्यता से सम्बन्ध रखता है।अर्थात् उसका लक्ष्य वास्तविक दृष्टि से वाक्यों को आधार रूप में लेकर उनसे वास्तविक रूप में सत्य निष्कर्षों को प्राप्त करना है।इसलिए अनुमान में आधार-वाक्यों को सत्य मान नहीं लिया जाता बल्कि उन्हें वास्तविक अनुभव के द्वारा प्राप्त किया जाता है।
प्रश्न:2.निगनात्मक तर्क से क्या तात्पर्य है? (What is Meant by Deductive Reasoning?):
उत्तर:सामान्य सिद्धान्त से विशेष निष्कर्ष निकालने की प्रक्रिया को निगमन तर्क कहते हैं।निगमन तर्क शास्त्र में आकारिक सत्यता से मतलब रहता है।
प्रश्न:3.व्लादिमीर अर्नोल्ड के अनुसार गणित में उपपत्ति की परिभाषा क्या है? (What is Definition of Proofs in Mathematics According to VLADIMIR ARNOLD?):
उत्तर:गणित के लिए प्रमाण वही हैं जो कविता के लिए सुलेख का है। गणितीय कार्यों में प्रमाण शामिल होते हैं जैसे कविताओं में पात्र होते हैं।
-व्लादिमीर अर्नोल्ड
(Proofs are to mathematics what calligraphy is to poetry.mathematical works do consist of proofs just as poems do consist of characters.
-VLADIMIR ARNOLD)
उपर्युक्त प्रश्नों के उत्तर द्वारा गणित में उपपत्तियाँ (Proofs in Mathematics),गणित में उपपत्तियाँ कक्षा 12 (Proofs in Mathematics Class 12) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Proofs in Mathematics
गणित में उपपत्तियाँ (Proofs in Mathematics)
Proofs in Mathematics
गणित में उपपत्तियाँ (Proofs in Mathematics) के इस आर्टिकल में गणितीय
साध्यों को सिद्ध (प्रमाणित) करने की विभिन्न विधियों के बारे में अध्ययन करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.