Polar form of complex number class 11
1.सम्मिश्र संख्याओं का ध्रुवीय रूप (Polar form of complex number class 11,Polar form of complex numbers)-
सम्मिश्र संख्याओं का ध्रुवीय रूप (Polar form of complex number class 11,Polar form of complex numbers) में निरूपण करना सीखेंगे।एक सम्मिश्र संख्या z को बिन्दु रूप में जिस समतल में निरूपित किया जाता है उस समतल में स्थित प्रत्येक बिन्दु के संगत एक अद्वितीय सम्मिश्र संख्या निरूपित होती है।इस समतल को सम्मिश्र समतल या आर्गेण्ड समतल (Argand plane) कहते हैं।
(1.) ध्रुवीय निरूपण (Polar representation),ध्रुवीय रूप समीकरण (Polar form equation),ध्रुवीय रूप सूत्र (Polar form formula)-
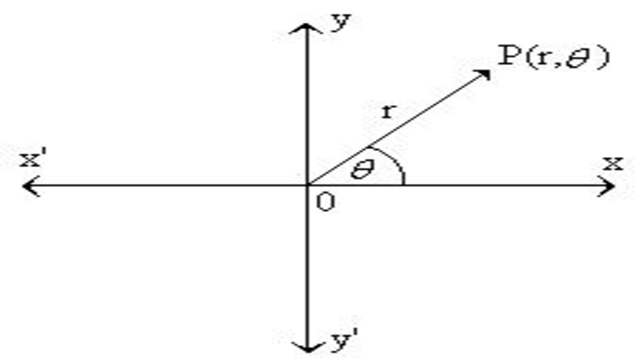
माना P(a,b) सम्मिश्र संख्या z=a+ib\neq 0 को निरूपित करता है। जहां माना OP=r तथा OP,x-अक्ष की धनात्मक दिशा से \theta कोण बनाता है।तब P को वास्तविक संख्याओं के एक अद्वितीय क्रमित युग्म \left( r,\theta \right) से निरूपित किया जा सकता है जो कि बिन्दु P के ध्रुवीय निर्देशांक कहलाते हैं। ध्रुवीय निर्देशांक में मूलबिन्दु O को ध्रुव तथा अर्धअक्ष OX को प्रारम्भिक रेखा कहते हैं।
यहां \frac { a }{ r } =\cos { \theta } ,\frac { b }{ r } =\sin { \theta } \\ \Rightarrow z=r\cos { \theta } +i r\sin { \theta }
एवं \tan { \theta } =\frac { b }{ a }
यह सम्मिश्र संख्या z का ध्रुवीय रूप कहलाता है। यहां r=\sqrt { { a }^{ 2 }+{ b }^{ 2 } } =\left| z \right| तथा \theta =\tan ^{ -1 }{ \frac { b }{ a } } क्रमशः सम्मिश्र संख्या के मापांक एवं कोणांक कहलाते हैं।
(2.)किसी सम्मिश्र संख्या का कोणांक अद्वितीय नहीं होता है।यदि सम्मिश्र संख्या z\neq 0 का कोणांक \theta है तो \theta +2n\pi जहां n\epsilon I भी उसके कोणांक हैं।किसी सम्मिश्र संख्या z\neq 0 के लिए अन्तराल 0\le \theta \le 2\pi में \theta का केवल एक मान प्राप्त होता है।
परन्तु हम कोणांक को निर्धारित करने हेतु 2\pi अन्तराल अर्थात् -\pi <\theta \le \pi काम में लेते हैं।सम्मिश्र संख्या z\neq 0 के कोणांक \theta का वह मान जो कि अन्तराल-\pi <\theta \le \pi में स्थित है मुख्य कोणांक कहलाता है।
(3.)सूत्र \theta =\tan ^{ -1 }{ \frac { b }{ a } } ,कोणांक \theta ज्ञात करने के लिए अपूर्ण सूत्र है।
उदाहरणार्थ:सम्मिश्र संख्या { z }_{ 1 }=\sqrt { 3 } +i तथा { z }_{ 2 }=-\sqrt { 3 } -i सम्मिश्र संख्या आर्गेण्ड समतल में दो अलग-अलग बिन्दुओं को प्रकट करते हैं जबकि उपर्युक्त सूत्र से उनका कोणांक \frac { \pi }{ 6 } प्राप्त होता है।
(4.)सम्मिश्र संख्या z का कोणांक उस चतुर्थांश (Quadrant) पर निर्भर करता है जिसमें z स्थित है अतः
(a) यदि a>0,b>0 (प्रथम चतुर्थांश) तब कोणांक z=\tan ^{ -1 }{ \frac { b }{ a } }
(b)यदि a<0,b>0 (द्वितीय चतुर्थांश) तब कोणांक z=\pi -\tan ^{ -1 }{ \left| \frac { b }{ a } \right| }
(c)यदि a<0,b<0 (तृतीय चतुर्थांश) तब कोणांक z=-\pi +\tan ^{ -1 }{ \left| \frac { b }{ a } \right| }
(d) यदि a>0,b<0 (चतुर्थ चतुर्थांश) तब कोणांक z=-\tan ^{ -1 }{ \left| \frac { b }{ a } \right| }
(5.)सम्मिश्र संख्या 0 का कोणांक अपरिभाषित है।
(6.)सम्मिश्र संख्या के ध्रुवीय रूप r\left( \cos { \theta } +i\sin { \theta } \right) की कुछ विशेष स्थितियां
(a)1=\cos { 0 } +i\sin { 0 } \qquad \qquad (b)-1=\cos { \pi } +i\sin { \pi } \\ \left( c \right) i=\cos { \frac { \pi }{ 2 } } +i\sin { \frac { \pi }{ 2 } } \qquad \left( d \right) -i=\cos { \left( -\frac { \pi }{ 2 } \right) } +i\sin { \left( -\frac { \pi }{ 2 } \right) }
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Middle term of binomial expansion
2.निम्न सम्मिश्र संख्याओं के कोणांक ज्ञात कीजिए:
(Find the argument of the following complex numbers:)
Example-1.\frac { 1+i }{ 1-i }
Solution–\frac { 1+i }{ 1-i } \\ =\frac { 1+i }{ 1-i } \times \frac { 1+i }{ 1+i } \\ =\frac { 1+2i+{ i }^{ 2 } }{ 1-{ i }^{ 2 } } \\ =\frac { 1+2i-1 }{ 1+1 } \\ =\frac { 2i }{ 2 } \\ =i\\ =0+i\\ b=1,a=0
कोणांक z=\tan ^{ -1 }{ \left| \frac { b }{ a } \right| }
कोणांक z=\tan ^{ -1 }{ \left| \frac { 1 }{ 0 } \right| } \\ =\tan ^{ -1 }{ \infty } \\ =\frac { \pi }{ 2 }
Example-2.-1+\sqrt { 3 } i
Solution–-1+\sqrt { 3 } i\\ b=\sqrt { 3 } ,a=-1
द्वितीय चतुर्थांश में है।
अतः कोणांक z=\pi -\tan ^{ -1 }{ \left| \frac { b }{ a } \right| } \\ =\pi -\tan ^{ -1 }{ \left| \frac { \sqrt { 3 } }{ -1 } \right| } \\ =\pi -\tan ^{ -1 }{ \sqrt { 3 } } \\ =\pi -\frac { \pi }{ 3 } \\ =\frac { 2\pi }{ 3 }
Example-3.\frac { 5+i\sqrt { 3 } }{ 4-i2\sqrt { 3 } }
Solution–\frac { 5+i\sqrt { 3 } }{ 4-i2\sqrt { 3 } } \\ =\frac { 5+i\sqrt { 3 } }{ 4-i2\sqrt { 3 } } \times \frac { 4+i2\sqrt { 3 } }{ 4+i2\sqrt { 3 } } \\ =\frac { 20+i10\sqrt { 3 } +i4\sqrt { 3 } +6{ i }^{ 2 } }{ { 4 }^{ 2 }-12{ i }^{ 2 } } \\ =\frac { 20+i14\sqrt { 3 } -6 }{ 16+12 } \\ =\frac { 14+i14\sqrt { 3 } }{ 28 } =\frac { 14(1+i\sqrt { 3 } ) }{ 28 } \\ =\frac { 1 }{ 2 } +i\frac { \sqrt { 3 } }{ 2 } \\ a=\frac { 1 }{ 2 } ,b=\frac { \sqrt { 3 } }{ 2 }
प्रथम चतुर्थांश में है अतः कोणांक z=\tan ^{ -1 }{ \left| \frac { b }{ a } \right| }
कोणांक z=\tan ^{ -1 }{ \left| \frac { \frac { \sqrt { 3 } }{ 2 } }{ \frac { 1 }{ 2 } } \right| } \\ =\tan ^{ -1 }{ \sqrt { 3 } } \\ =\frac { \pi }{ 3 }
3.सम्मिश्र संख्याओं का ध्रुवीय रूप के उदाहरण (Polar form of complex number class 11 examples,Polar form of complex numbers examples),ध्रुवीय रूप में परिवर्तित करें (Convert to polar form)-
निम्न सम्मिश्र संख्याओं को ध्रुवीय रूप में व्यक्त कीजिए:
(Express the following complex numbers in polar form:)
Example-4.\frac { 1+i }{ \sqrt { 2 } }
Solution–\frac { 1+i }{ \sqrt { 2 } } \\ \Rightarrow \frac { 1 }{ \sqrt { 2 } } +\frac { 1 }{ \sqrt { 2 } } \iota =r(\cos { \theta } +\iota \sin { \theta } )\\ r\cos { \theta } =\frac { 1 }{ \sqrt { 2 } } ,r\sin { \theta } =\frac { 1 }{ \sqrt { 2 } }
वर्ग करके जोड़ने पर-
{ r }^{ 2 }\cos ^{ 2 }{ \theta } +{ r }^{ 2 }\sin ^{ 2 }{ \theta } ={ \left( \frac { 1 }{ \sqrt { 2 } } \right) }^{ 2 }+{ \left( \frac { 1 }{ \sqrt { 2 } } \right) }^{ 2 }\\ { r }^{ 2 }=\frac { 1 }{ 2 } +\frac { 1 }{ 2 } =1\\ r=1\\ a=\frac { 1 }{ \sqrt { 2 } } ,b=\frac { 1 }{ \sqrt { 2 } }
प्रथम चतुर्थांश में है अतः \theta =\tan ^{ -1 }{ \frac { b }{ a } } \\ \theta =\tan ^{ -1 }{ \frac { \frac { 1 }{ \sqrt { 2 } } }{ \frac { 1 }{ \sqrt { 2 } } } } \\ \theta =\tan ^{ -1 }{ (1) } \\ \theta =\frac { \pi }{ 4 }
अतः \frac { 1+i }{ \sqrt { 2 } } का ध्रुवीय रूप=\left( \cos { \frac { \pi }{ 4 } } +i\sin { \frac { \pi }{ 4 } } \right)
Example-5.\frac { 1+7i }{ (2-{ \iota ) }^{ 2 } }
Solution:-\frac { 1+7i }{ (2-{ \iota ) }^{ 2 } } \\ \frac { 1+7i }{ 4-4i+{ \iota }^{ 2 } } \\ =\frac { 1+7i }{ 4-4i-1 } \\ =\frac { 1+7i }{ 3-4i } \\ =\frac { 1+7i }{ 3-4i } \times \frac { 3+4i }{ 3+4i } \\ =\frac { 3+4i+21i+28{ \iota }^{ 2 } }{ { 3 }^{ 2 }-{ (4i) }^{ 2 } } \\ =\frac { 3+25i-28 }{ 9-{ 16\iota }^{ 2 } } \\ =\frac { -25+25i }{ 9+16 } \\ =\frac { 25(-1+i) }{ 25 } \\ =-1+i=r\left( \cos { \theta } +i\sin { \theta } \right) \\ r\cos { \theta } =-1,r\sin { \theta } =1
वर्ग करके जोड़ने पर-
{ r }^{ 2 }\cos ^{ 2 }{ \theta } +{ r }^{ 2 }\sin ^{ 2 }{ \theta } ={ \left( -1 \right) }^{ 2 }+{ \left( 1 \right) }^{ 2 }\\ \Rightarrow { r }^{ 2 }=1+1\\ \Rightarrow { r }^{ 2 }=2\\ r=\sqrt { 2 } \\ a=-1,b=1
अतः द्वितीय चतुर्थांश में है।
\theta =\pi -\tan ^{ -1 }{ \left| \frac { b }{ a } \right| } \\ =\pi -\tan ^{ -1 }{ \left| \frac { -1 }{ 1 } \right| } \\ =\pi -\tan ^{ -1 }{ 1 } \\ =\pi -\frac { \pi }{ 4 } \\ =\frac { 3\pi }{ 4 }
अतः \frac { 1+7i }{ (2-{ i) }^{ 2 } } का ध्रुवीय रूप=\sqrt { 2 } \left( \cos { \frac { 3\pi }{ 4 } } +i\sin { \frac { 3\pi }{ 4 } } \right)
Example-6.\cos { \frac { \pi }{ 3 } } +i\sin { \frac { \pi }{ 3 } }
Solution–\cos { \frac { \pi }{ 3 } } +i\sin { \frac { \pi }{ 3 } } \\ \Rightarrow \frac { \sqrt { 3 } }{ 2 } +i\frac { 1 }{ 2 } =r\left( \cos { \theta } +i\sin { \theta } \right) \\ r\cos { \theta } =\frac { \sqrt { 3 } }{ 2 } ,r\sin { \theta } =\frac { 1 }{ 2 }
वर्ग करके जोड़ने पर-
{ r }^{ 2 }\cos ^{ 2 }{ \theta } +{ r }^{ 2 }\sin ^{ 2 }{ \theta } ={ \left( \frac { \sqrt { 3 } }{ 2 } \right) }^{ 2 }+{ \left( \frac { 1 }{ 2 } \right) }^{ 2 }\\ \Rightarrow { r }^{ 2 }=\frac { 3 }{ 4 } +\frac { 1 }{ 4 } \\ \Rightarrow { r }^{ 2 }=\frac { 4 }{ 4 } =1\\ \Rightarrow r=1\\ a=\frac { \sqrt { 3 } }{ 2 } ,b=\frac { 1 }{ 2 }
अतः प्रथम चतुर्थांश में है।
\theta =\tan ^{ -1 }{ \frac { b }{ a } } \\ =\tan ^{ -1 }{ \frac { \frac { 1 }{ 2 } }{ \frac { \sqrt { 3 } }{ 2 } } } \\ \Rightarrow \theta =\tan ^{ -1 }{ \frac { 1 }{ \sqrt { 3 } } } =\frac { \pi }{ 6 }
अतः \cos { \frac { \pi }{ 3 } } +i\sin { \frac { \pi }{ 3 } } का ध्रुवीय रूप=\left( \cos { \frac { \pi }{ 6 } } +i\sin { \frac { \pi }{ 6 } } \right)
उपर्युक्त उदाहरणों के द्वारा सम्मिश्र संख्याओं का ध्रुवीय रूप (Polar form of complex number class 11,Polar form of complex numbers) को समझा जा सकता है।
4.सम्मिश्र संख्याओं का ध्रुवीय रूप की समस्याएं (Problems of Polar form of complex numbers)-
निम्न सम्मिश्र संख्याओं को ध्रुवीय रूप में व्यक्त कीजिए:
(Express the following complex numbers in polar form:)
(1)1+20i\\ (2)-\frac { 7 }{ 2 } +\frac { i }{ 2 } \\ (3)\sqrt { 3 } +i\\ (4)\frac { i }{ 3 } -\frac { 3 }{ i } \\ (5)-\frac { 3 }{ 2 } +i\frac { 3\sqrt { 3 } }{ 2 } \\ (6)\sin { \frac { \pi }{ 5 } } +i(1-\cos { \frac { \pi }{ 5 } } )
उत्तर-(1)\sqrt { 401 } \left( \cos { (\tan ^{ -1 }{ 20 } ) } +i\sin { (\tan ^{ -1 }{ 20 } ) } \right) \\ (2)\frac { 25 }{ 2 } \left( \cos { (\pi -\tan ^{ -1 }{ (\frac { 1 }{ 7 } ) } ) } +i\sin { (\pi -\tan ^{ -1 }{ (\frac { 1 }{ 7 } ) } ) } \right) \\ (3)2\left( \cos { \frac { \pi }{ 6 } } +i\sin { \frac { \pi }{ 6 } } \right) \\ (4)\frac { 10 }{ 3 } \left( \cos { \frac { \pi }{ 2 } } +i\sin { \frac { \pi }{ 2 } } \right) \\ (5)3\left( \cos { \frac { 2\pi }{ 3 } } +i\sin { \frac { 2\pi }{ 3 } } \right) \\ (6)2\sin { \frac { \pi }{ 10 } } \left( \cos { \frac { \pi }{ 10 } } +i\sin { \frac { \pi }{ 10 } } \right)
इन समस्याओं को हल करने पर सम्मिश्र संख्याओं का ध्रुवीय रूप (Polar form of complex number class 11,Polar form of complex numbers) ओर अधिक ठीक से समझ में आ सकता है।
5.ध्रुवीय रूप से आयताकार रूप (Polar form to rectangular form)-
ध्रुवीय रूप से आयताकार रूप में बदलना ध्रुवीय से आयताकार में बदलने के लिए, कोण के कोसाइन द्वारा ध्रुवीय परिमाण को गुणा करके और कोण के साइन द्वारा ध्रुवीय परिमाण को गुणा करके काल्पनिक घटक का वास्तविक घटक ढूंढें।
6.आयताकार रूप में सम्मिश्र संख्या (Complex number to rectangular form)-
एक सम्मिश्र संख्या का आयताकार प्रतिनिधित्व z = a + bi के रूप में है।यदि आप अपने कार्टेशियन निर्देशांक के अनुसार एक सम्मिश्र संख्या का प्रतिनिधित्व करते थे, तो यह फॉर्म में होगा: (a, b);जहाँ a वास्तविक भाग, x-अक्ष और काल्पनिक भाग b, y अक्ष के साथ स्थित है।
7.सम्मिश्र संख्या कोणांक का ध्रुवीय रूप (Polar form of complex numbers argument)-
ध्रुवीय रूप में एक जटिल संख्या z को r (cosθ+isinθ) के रूप में दिया जाता है और अक्सर इसे rcosθ के रूप में संक्षिप्त किया जाता है, जहाँ r सम्मिश्र संख्या के मापांक के बराबर होता है।θ के मान, को z का कोणांक कहा जाता है, जिसे arg (z) द्वारा चिह्नित किया जाता है।ध्यान दें कि r(cos(θ+2kπ)+isin(θ+2kπ)) प्रत्येक पूर्णांक k के लिए एक ही सम्मिश्र संख्या का प्रतिनिधित्व करता है।
8.आप ध्रुवीय रूप में कैसे परिवर्तित करते हैं? (How do you convert to polar form?)-
ध्रुवीय निर्देशांक (r, θ) से कार्तीय निर्देशांक (x, y) में परिवर्तित करने के लिए:
x = r × cos (θ)
y = r × sin (θ)
कार्तीय निर्देशांक (x, y) से ध्रुवीय निर्देशांक (r, θ) में परिवर्तित करने के लिए:
{ r }^{ 2 }={ x }^{ 2 }+{ y }^{ 2 }
\theta =\tan ^{ -1 }{ (\frac { y }{ x } ) }
\theta =\tan ^{ -1 }{ (\frac { y }{ x } ) } के मूल्य को समायोजित करने की आवश्यकता हो सकती है:
चतुर्थांश I: कैलकुलेटर मान का उपयोग करें
चतुर्थांश II: 180 ° जोड़ें
चतुर्थांश III: 180 ° जोड़ें
चतुर्थांश IV: 360 ° जोड़ें
9. क्या आप ध्रुवीय रूप में सम्मिश्र संख्या जोड़ सकते हैं?(Can you add complex numbers in polar form?)-
आयताकार रूप में सम्मिश्र संख्याओं को जोड़ने के लिए, वास्तविक घटकों को जोड़ें और काल्पनिक घटकों को जोड़ें।घटाव समान है।ध्रुवीय रूप में सम्मिश्र संख्याओं को गुणा करने के लिए, परिमाणों को गुणा करें और कोणों को जोड़ें।
10.ध्रुवीय और आयताकार रूप क्या है? (What is polar and rectangular form?)-
आयताकार फॉर्म में एक सम्मिश्र संख्या को सम्मिश्र तल पर अंतरिक्ष में एक बिंदु द्वारा दर्शाया जाता है।पोलर फॉर्म में एक सम्मिश्र संख्या को एक रेखा द्वारा दर्शाया जाता है जिसकी लंबाई आयाम और चरण कोण द्वारा होती है।
उपर्युक्त प्रश्नों के उत्तर द्वारा आप सम्मिश्र संख्याओं का ध्रुवीय रूप (Polar form of complex number class 11,Polar form of complex numbers) को भली-भांति समझ सकते हैं।
Also Read This Article:-Trigonometric functions of two angles
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |