Theorem of Total Probability
1.सम्पूर्ण प्रायिकता का प्रमेय (Theorem of Total Probability),बेज प्रमेय (Baye’s Theorem):
सम्पूर्ण प्रायिकता का प्रमेय (Theorem of Total Probability):(1.)एक प्रतिदर्श समष्टि का विभाजन (Partition of a Sample Space):
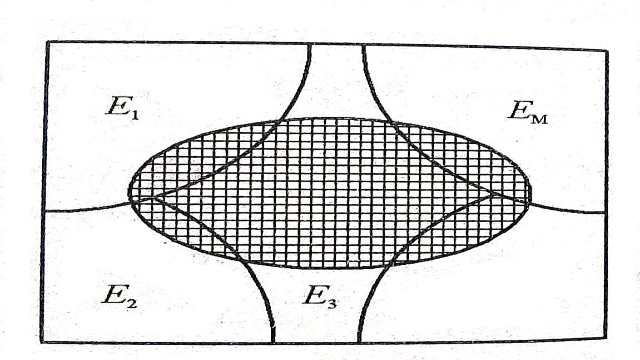
घटनाओं E_{1}, E_{2}, E_{3} \ldots, E_{n} का समुच्चय प्रतिदर्श समष्टि S के विभाजन को निरूपित करता है यदि:
(i)E_{i} \cap E_{j}=\phi, \quad i=j, i, j=1,2,3,\ldots, n
(ii)E_{1} \cup E_{2} \cup E_{3} \cup \ldots \cup E_{n}=S तथा
(iii)P\left(E_{i}\right)>0 प्रत्येक i=1,2,3,……,n
के लिए दूसरे शब्दों में घटनाएं E_{1}, E_{2}, E_{3} \ldots, E_{n} प्रतिदर्श समष्टि S के विभाजन को निरूपित करती है।यदि वे युग्मत: असंयुक्त हैं; समग्र हैं तथा उनकी प्रायिकता शून्येतर है।
(2.)सम्पूर्ण प्रायिकता का प्रमेय (Theorem of Total Probability):
कथन (Statement):माना \left\{E_{1},E_{2}, E_{3}, \ldots,E_{n}\right\} प्रतिदर्श समष्टि S का एक विभाजन और प्रत्येक घटना E_{1}, E_{2}, E_{3} \ldots, E_{n} की प्रायिकता शून्येतर है।मान लीजिए A प्रतिदर्श समष्टि के संगत एक घटना है, तब
P(A)=P\left(E_{1}\right) P\left(\frac{A}{E_{1}}\right)+P\left(E_{2}\right) P\left(\frac{A}{E_{2}}\right)+P\left(E_{3}\right) P\left(\frac{A}{E_{3}}\right)+\cdots \cdot + P\left(E_{n}\right) P\left(\frac{A}{E_{n}}\right) \\ =\sum_{j=1}^{n} P\left(E_{j}\right) P\left(\frac{A}{E_{j}}\right)
प्रमाण (Proof):दिया है E_{1}, E_{2}, E_{3} \ldots, E_{n} प्रतिदर्श समष्टि S का एक विभाजन है।
S=E_{1} \cup E_{2} \cup E_{3} \cup \ldots \cup E_{n} \cdots(1)
और E_{i} \cap E_{j}=\phi \forall i \neq j, i, j=1, 2,3, \cdots, n
ज्ञात है कि किसी घटना A के लिए
A=A \cap S \\ =A \cap \left(E_{1} \cup E_{2} \cup E_{3} \cup \ldots \cup E_{n}\right) \\ =\left(A \cap E_{1}\right) \cup\left(A \cap E_{2}\right) \cup\left(A \cap E_{3}\right) \cup \ldots \cup \left(A \cap E_{n}\right) \\ A \cap E_{i} और A \cap E_{j} क्रमशः समुच्चयों E_{i} और E_{j} के उपसमुच्चय हैं जो i \neq j के लिए असंयुक्त हैं।
i \neq j , i, j=1,2,3, \cdots, n के लिए A \cap E_{i} और A \cap E_{j} भी असंयुक्त हैं।
P(A)=P\left[\left(A \cap E_{1}\right) \cup\left(A \cup E_{2}\right) \cup\left(A \cap E_{3}\right)\cup \ldots \cup \left(A \cap E_{n}\right)\right]\\ =P\left(A \cap E_{1}\right)+P\left(A \cap E_{2}\right)+P\left(A \cap E_{3}\right)+ \ldots+P\left(A \cap E_{n}\right)
अब P\left(A \cap E_{i}\right)=P(E_{i}) P\left(\frac{A}{E_{i}}\right)\left[\because P\left(E_{i}\right) \neq 0 \forall i=1,2,3,\ldots,n\right]
प्रायिकता के गुणन नियम से:
P(A)=P(E_{1}) P\left(\frac{A}{E_{1}}\right)+P\left(E_{2}\right) P\left(\frac{A}{E_{2}}\right)+P\left(E_{3}\right) P\left(\frac{A}{E_{3}}\right)+\ldots+P\left(E_{n}\right) P\left(\frac{A}{E_{n}}\right)
या P(A)=\sum_{j=1}^{n} P\left(E_{j}\right) P\left(\frac{A}{E_{j}}\right)
(3.)बेज प्रमेय (Baye’s Theorem):
गणितज्ञ जाॅन बेज ने प्रतिलोम प्रायिकता ज्ञात करने की समस्या का समाधान सप्रतिबन्ध प्रायिकता में उपयोग द्वारा किया है।उनके द्वारा बनाया गया सूत्र ‘बेज प्रमेय’ के नाम से जाना जाता है।
कथन (Statement):यदि E_{1}, E_{2}, E_{3} \ldots, E_{n} अरिक्त घटनाएँ हैं जो कि प्रतिदर्श समष्टि S के विभाजन का निर्माण करती है अर्थात् E_{1}, E_{2}, E_{3}, \ldots, E_{n} युग्मत: असंयुक्त है E_{1} \cup E_{2} \cup E_{3} \cup, \ldots ,\cup E_{n}=S और A कोई ऐसी घटना है कि जिसकी प्रायिकता शून्येतर है तो
P\left(\frac{E_{i}}{A}\right) = \frac{P\left(E_{i}\right) P\left(\frac{A}{E_{i}}\right)}{\sum_{j=1}^{n} P\left(E_{j}\right) P\left(\frac{A}{E_{j}}\right)},i=1,2,3,\ldots,n
प्रमाण (Proof):हम जानते हैं कि
P\left(\frac{E_{i}}{A}\right) =\frac{P\left(A \cap E_{j}\right)}{P(A)} \\ =P(E_{i}) P\left(\frac{A}{E_{i}}\right) (प्रायिकता के गुणन नियम से)
=\frac{P\left(E_{i}\right) P\left(\frac{A}{E_{i}}\right)}{\sum_{j=1}^{n} P\left(E_{j}\right) P\left(\frac{A}{E_{j}}\right)}(सम्पूर्ण प्रायिकता के नियम से)
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Conditional Probability
2.सम्पूर्ण प्रायिकता का प्रमेय के उदाहरण (Theorem of Total Probability Examples):
Example:1.दो थैले I व II दिए गए हैं।थैले I में 3 लाल और 4 काली गेंदें हैं जबकि II थैले में 5 लाल और 6 काली गेंदे हैं।किसी एक थैले में से यादृच्छया एक गेंद निकाली गई है जो कि लाल है।इस बात की क्या प्रायिकता है कि यह गेंद II थैले से निकाली गई है?
Solution:माना थैले I को E_{1} तथा थैले II को E_{2} से निरूपित करते हैं और लाल रंग की गेंद निकालने की घटना को A से निरूपित करते हैं।
तब P\left(E_{1}\right)=P\left(E_{2}\right)=\frac{1}{2}
थैले I में से लाल रंग की गेंद निकालने की प्रायिकता
P\left(\frac{A}{E_{1}}\right)=\frac{3}{7}
और थैले II में से लाल रंग की गेंद निकालने की प्रायिकता
P\left(\frac{A}{E_{2}}\right)=\frac{5}{11}
थैले II में से गेंद निकालने की प्रायिकता जब वह लाल रंग की है=P\left(\frac{E_{2}}{A}\right)
बेज प्रमेय से:
P\left(\frac{E_{2}}{A}\right)=\frac{P\left(E_{2}\right) P\left(\frac{A}{E_{2}}\right)}{P\left(E_{1}\right) P\left(\frac{A}{E}_{1}\right)+P\left(E_{2}\right) P\left(\frac{A}{E_{2}}\right)} \\ =\frac{\frac{1}{2} \times \frac{5}{11}}{\frac{1}{2} \times \frac{3}{7}+\frac{1}{2} \times \frac{5}{11}} \\ =\frac{\frac{5}{22}}{\frac{3}{14}+\frac{5}{22}}\\ =\frac{\frac{5}{22}}{\frac{33+35}{154}} \\ =\frac{\frac{5}{22}}{\frac{68}{154}} \\ =\frac{5}{22} \times \frac{154}{68} \\ =\frac{35}{68}
Example:2.एक डॉक्टर को एक रोगी को देखने आना है।पहले के अनुभवों से यह ज्ञात है कि उसके ट्रेन,बस,स्कूटर या अन्य किसी वाहन से आने की प्रायिकताएँ \frac{3}{10}, \frac{1}{5}, \frac{1}{10} या \frac{2}{5} है।यदि वह ट्रेन,बस या स्कूटर से आता है तो उसके देर से आने की प्रायिकताएँ क्रमशः \frac{1}{4},\frac{1}{3} या \frac{1}{12} है परन्तु किसी अन्य वाहन से आने से पर उसे देर नहीं होती है।यदि वह देर से आया तो उसके ट्रेन से आने की प्रायिकता ज्ञात कीजिए।
Solution:माना “डाॅक्टर के रोगी के यहाँ देर से आने” की घटना E है।यदि डाॅक्टर के ट्रेन,बस,स्कूटर या किसी अन्य वाहन द्वारा आने की घटनाएँ क्रमशः E_{1},E_{2},E_{3} और E_{4} हैं तो
दिया है: P\left(E_{1}\right)=\frac{3}{10} P\left(E_{2}\right)=\frac{1}{5},P\left(E_{3}\right)=\frac{1}{10} और P\left(E_{4}\right)=\frac{2}{5}
P\left(\frac{E}{E_{1}}\right) =डॉक्टर के ट्रेन द्वारा आने पर देर से पहुँचने की प्रायिकता
P\left(\frac{E}{E_{1}}\right)=\frac{1}{4} इसी प्रकार P\left(\frac{E}{E_{2}}\right)=\frac{1}{3}, P\left(\frac{E}{E_{3}}\right)=\frac{1}{12}, P\left(\frac{E}{E_{4}}\right)=0
(अन्य वाहन से आने पर देर नहीं होती है)
अब बेज प्रमेय द्वारा
P\left(\frac{E_{1}}{E}\right)=डॉक्टर द्वारा देर से आने पर ट्रेन द्वारा आने की प्रायिकता
P\left(\frac{E_{1}}{E}\right)=\frac{P\left(E_{1}\right) \cdot P\left(\frac{E}{E_{1}}\right)}{P\left(E_{1}\right) \cdot P\left(\frac{E}{E_{1}}\right)+P\left(E_{2}\right) \cdot P\left(\frac{E}{E_{2}}\right)+P\left(E_{3}\right) \cdot P\left(\frac{E}{E_{3}}\right)+P\left(E_{4}\right) \cdot P\left(\frac{E}{E_{4}}\right)} \\ =\frac{\frac{3}{4} \times \frac{1}{4}}{\frac{3}{4} \times \frac{1}{4}+\frac{1}{5} \times \frac{1}{3}+\frac{1}{10} \times \frac{1}{12}+\frac{2}{5} \times 0} \\ =\frac{\frac{3}{40}}{\frac{3}{40}+\frac{1}{15}+\frac{1}{120}} \\ =\frac{\frac{3}{40}}{\frac{9+8+1}{120}} \\ =\frac{3}{40} \times \frac{120}{18} \\ \Rightarrow P\left(\frac{E_{1}}{E}\right) =\frac{1}{2}
Example:3.प्रथम थैले में 3 लाल और 4 काली गेंदें हैं जबकि द्वितीय थैले में 4 लाल और 5 काली गेंदें है।एक गेंद प्रथम थैले से द्वितीय थैले में स्थानान्तरित की जाती है और तब एक गेंद को द्वितीय थैले से निकाला जाता है।निकाली गई गेंद लाल रंग की प्राप्त होती है।इस बात की क्या प्रायिकता है कि स्थानान्तरित गेंद काली है?
Solution:माना थैले I से स्थानान्तरित लाल गेंद होने की घटना=E_{1}
तथा काली गेंद होने की घटना E_{2} है।
यदि II थैले से लाल गेंद निकालने की घटना E है तो
P\left (E_{1} \right )=\frac{3}{7},P\left ( E_{2} \right )=\frac{4}{7}
स्थानान्तरित गेंद लाल हो तो थैले II से लाल गेंद निकालने की प्रायिकता:
P\left(\frac{E}{E_{1}}\right)=\frac{5}{10}=\frac{1}{2}
स्थानान्तरित गेंद काली हो तो थैले II से लाल गेंद निकालने की प्रायिकता:
P\left(\frac{E}{E_{2}}\right)=\frac{4}{10}=\frac{2}{5}
थैले II से लाल रंग की गेंद है तो स्थानान्तरित गेंद के काली रंग की होने की प्रायिकता=P\left(\frac{E_{2}}{E}\right)
बेज प्रमेय से:
P\left(\frac{E_{2}}{E}\right)=\frac{P\left(E_{2}\right) \cdot P\left(\frac{E}{E_{2}}\right)}{P\left(E_{1}\right) \cdot P\left(\frac{E}{E_{1}}\right)+P\left(E_{2}\right) \cdot P\left(\frac{E}{E_{2}}\right)} \\ =\frac{\frac{4}{7} \times \frac{2}{5}}{\frac{3}{7} \times \frac{1}{2}+\frac{4}{7} \times \frac{2}{5}} \\ =\frac{\frac{8}{35}}{\frac{3}{14}+\frac{8}{35}} \\ =\frac{\frac{8}{35}}{\frac{15+16}{70}} \\ =\frac{\frac{8}{35}}{\frac{31}{70}} \\ =\frac{8}{35} \times \frac{70}{31} \\ P\left(\frac{E_{2}}{E}\right)=\frac{16}{31}
Example:4.एक थैले में 4 लाल और 4 काली गेंदें हैं और एक अन्य थैले में 2 लाल और 6 काली गेंदें हैंं।इन दोनों थैलों में से एक थैले को यादृच्छया चुना जाता है और उसमें से एक गेंद निकाली जाती है जो कि लाल है।इस बात की क्या प्रायिकता है कि गेंद पहले थैले से निकाली गई है?,
Solution:माना पहले थैले से गेंद निकालने की घटना तथा अन्य थैले से गेंद निकालने की घटना है।यदि लाल रंग की गेंद निकालने की घटना E है तो
P\left(E_{1} \right)=P\left(E_{2}\right)=\frac{1}{2}
पहले थैले से लाल रंग की गेंद निकालने की प्रायिकता
P\left(\frac{E}{E_{1}}\right)=\frac{4}{8}=\frac{1}{2}
अन्य थैले से लाल रंग की गेंद निकालने की प्रायिकता:
P\left(\frac{E}{E_{2}}\right)=\frac{2}{8}=\frac{1}{4}
पहले थैले में से गेंद निकालने की प्रायिकता जब वह लाल रंग की है=P\left(\frac{E_{1}}{E}\right)
बेज प्रमेय से:
P\left(\frac{E_{1}}{E}\right) =\frac{P\left(E_{1}\right) \cdot P\left(\frac{E}{E_{1}}\right) }{P\left(E_{1}\right) \cdot P\left(\frac{E}{E_{1}}\right)+P\left(E_{2}\right) \cdot P\left(\frac{E}{E_{2}}\right)} \\ =\frac{\frac{1}{2} \times \frac{1}{2}}{\frac{1}{2} \times \frac{1}{2}+\frac{1}{2} \times \frac{1}{4}} \\ =\frac{\frac{1}{4}}{\frac{1}{4}+\frac{1}{8}} \\ =\frac{\frac{1}{4}}{\frac{2+1}{8}} \\ =\frac{1}{4} \times \frac{8}{3} \\ \Rightarrow P\left(\frac{E_{1}}{E}\right) =\frac{2}{3}
Example:5.तीन सिक्के दिए गए हैं एक सिक्के के दोनों ओर चित है।दूसरा सिक्का अभिनत है जिसमें चित 75% बार प्रकट होता है और तीसरा सिक्का अनभिनत है।तीनों सिक्कों में से एक सिक्के को यादृच्छया चुना गया और उसे उछाला गया।यदि सिक्के पर चित प्रकट हो तो इस बात की क्या प्रायिकता है कि वह दोनों चित वाला सिक्का है?
Solution:यदि तीनों सिक्को को चुनने की घटनाएँ E_{1},E_{2},E_{3} हैं तथा चित आने की घटना A है।तब
P\left(E_{1}\right)=P\left(E_{2}\right)=P\left(E_{3}\right)=\frac{1}{3}
पहले सिक्के के दोनों ओर चित है
अतः P\left(\frac{A}{E_{1}}\right)=1
दूसरा सिक्का इस प्रकार अभिनत है कि
P\left(\frac{A}{E_{2}}\right)=75 \%=\frac{75}{100}=\frac{3}{4}
तीसरा सिक्का अभिनत है
अतः P\left(\frac{A}{E_{2}}\right)=\frac{1}{2}
यदि सिक्के पर चित प्रकट हो तो इसके दोनों ओर चित वाला सिक्का होने की प्रायिकता
P\left(\frac{E_{1}}{A}\right)=\frac{P\left(E_{1}\right) \cdot P\left(\frac{A}{E_{1}}\right)}{P\left(E_{1}\right) \cdot P\left(\frac{A}{E_{1}}\right)+P\left(E_{2}\right) \cdot P\left(\frac{A}{E_{2}}\right)+P\left(E_{3}\right) \cdot P\left(\frac{A}{E_{3}}\right)} \\ =\frac{\frac{1}{3} \times 1}{\frac{1}{3} \times 1+\frac{1}{3} \times \frac{3}{4}+\frac{1}{3} \times \frac{1}{2}} \\ =\frac{\frac{1}{3}}{\frac{1}{3}+\frac{1}{4}+\frac{1}{6}} \\ =\frac{\frac{1}{3}}{\frac{4+3+2}{12}} \\ =\frac{1}{3} \times \frac{12}{9} \\ \Rightarrow P\left(\frac{E_{1}}{A}\right) =\frac{4}{9}
Example:6.किसी विशेष रोग के सही निदान के लिए रक्त की जाँच 99% असरदार है,जब वास्तव में रोगी उस रोग से ग्रस्त होता है।किन्तु 0.5% बार किसी स्वस्थ व्यक्ति की रक्त जाँच करने पर निदान गलत सूचना देता है यानी व्यक्ति को रोग से ग्रसित बताता है।यदि किसी जनसंख्या में 0.1% व्यक्ति उस रोग से ग्रस्त हैं तो क्या प्रायिकता है कि कोई यादृच्छया चुना गया व्यक्ति उस रोग से ग्रस्त होगा यदि उसके रक्त की जाँच में यह बताया जाता है कि उसे यह रोग है?
Solution:माना रोग से ग्रस्त रोगी की घटना=E_{1}
रोग से ग्रस्त रोगी नहीं की घटना=E_{2}
रोगी के रक्त की जाँच में रोग से ग्रस्त होने की घटना=A
\therefore रोग से ग्रस्त व्यक्ति की प्रायिकता
P\left(E_{1}\right)=0.1 \%=\frac{0.1}{100}=0.001
रोग से ग्रस्त नहीं व्यक्ति प्रायिकता
P\left(E_{2}\right) =1-P\left(E_{1}\right)=1-0.001 \\ \Rightarrow P\left(E_{2}\right) =0.999
उन व्यक्तियों की प्रायिकता जो रोगी है तथा रक्त की जाँच की गई
P\left(\frac{A}{E_{1}}\right)=99 \%=\frac{99}{100}=0.99
रक्त की जाँच की गई परन्तु व्यक्ति रोगी नहीं है कि प्रायिकता
P\left(\frac{A}{E_{2}}\right)=0.5 \%=\frac{0.5}{100}=0.005
कोई यादृच्छया चुना गया व्यक्ति रोग से ग्रस्त होगा यदि उसके रक्त की जाँच में रोग पाये जाने की प्रायिकता:
P\left(\frac{E_{1}}{A}\right)=\frac{P\left(E_{1}\right) \cdot P\left(\frac{A}{E_{1}}\right)}{P\left(E_{1}\right) \cdot P\left(\frac{A}{E_{1}}\right)+P\left(E_{2}\right) \cdot P\left(\frac{A}{E_{2}}\right)} \\ =\frac{0.001 \times 0.99}{0.001 \times 0.99+0.999 \times 0.005} \\ =\frac{0.00099}{0.00099+0.004995} \\ =\frac{0.000990}{0.0005985}=\frac{990}{5985}=\frac{198}{1197}=\frac{22}{133}
उपर्युक्त उदाहरणों के द्वारा सम्पूर्ण प्रायिकता का प्रमेय (Theorem of Total Probability),बेज प्रमेय (Baye’s Theorem) को समझ सकते हैं।
3.सम्पूर्ण प्रायिकता का प्रमेय की समस्याएं (Theorem of Total Probability Problems):
(1.)एक बोल्ट बनाने के कारखाने में मशीनें (यंत्र) A,B,C कुल उत्पादन का क्रमशः 25%,35% और 40% बोल्ट बनाती है।इन मशीनों के उत्पादन का क्रमशः 5,4 और 2 प्रतिशत त्रुटिपूर्ण है।बोल्टों के कुल उत्पादन में से एक बोल्ट यादृच्छया निकाला जाता है और वह त्रुटिपूर्ण पाया जाता है।इसकी क्या प्रायिकता है कि यह बोल्ट मशीन B द्वारा बनाया गया है?
(2.)तीन सर्वसम डिब्बे I,II और III दिए गए हैं।जहाँ प्रत्येक डिब्बे में दो सिक्के है।डिब्बे I में दोनों सिक्के सोने के है,डिब्बे II में दोनों सिक्के चाँदी के है और डिब्बे III में एक सोने और एक चाँदी का सिक्का है।एक व्यक्ति यादृच्छया एक डिब्बा चुनता है और उसमें से एक सिक्का निकालता है।यदि निकाला गया सिक्का सोने का है तो इस बात की क्या प्रायिकता है कि डिब्बे में दूसरा सिक्का भी सोने का है?
उत्तर (Answers):\text{(i)} \frac{28}{69} \\ \text{(ii)} \frac{2}{3}
उपर्युक्त सवालों को हल करने पर सम्पूर्ण प्रायिकता का प्रमेय (Theorem of Total Probability),बेज प्रमेय (Baye’s Theorem) को ठीक से समझ सकते हैं।
Also Read This Article:-Multiplication Theorem on Probability
4.सम्पूर्ण प्रायिकता का प्रमेय (Theorem of Total Probability),बेज प्रमेय (Baye’s Theorem) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.मान लीजिए 100 पुरुषों में से 5 और 1000 महिलाओं में से 25 वर्णान्ध (Colourblind) हैं।एक वर्णान्ध व्यक्ति को यादृच्छया चुन लिया गया तो वह एक पुरुष होगा, इसकी क्या प्रायिकता है?मान लिया गया है पुरुष और महिलाएं समानुपात में हैं।
उत्तर: E_{1} =पुरुष का होना, E_{2} =महिला का होना
A=वर्णान्ध का होना
P\left(\frac{A}{E_{1}}\right)=\frac{5}{100}=\frac{1}{20},P\left(\frac{A}{E_{2}}\right)=\frac{25}{1000}=\frac{1}{40},P\left(E_{1}\right)=P\left(E_{2}\right)=\frac{1}{2}\\ P\left(\frac{E_{1}}{A}\right) =\frac{P\left(E_{1}\right) \cdot P\left(\frac{A}{E_{1}}\right)}{P\left(E_{1}\right) \cdot P\left(\frac{A}{E_{1}}\right)+P\left(E_{2}\right) \cdot P\left(\frac{A}{E_{2}}\right)} \\=\frac{\frac{1}{2} \times \frac{1}{20}}{\frac{1}{2} \times \frac{1}{20} +\frac{1}{2} \times \frac{1}{40}} \\=\frac{\frac{1}{20}}{\frac{3}{40}}=\frac{2}{3}
प्रश्न:2.एक बोल्ट फैक्टरी में तीन मशीनें A,B,C क्रमशः 25%,35% और 40% बोल्ट का उत्पादन करती हैं।एक दिन के उत्पादन में पाया गया कि तीनों मशीनें क्रमशः 5%,4% और 2% खराब बोल्ट का उत्पादन करती है।पूर्ण उत्पादन में से एक बोल्ट यादृच्छया चुना गया यदि यह खराब है तो इसके मशीन A से उत्पादित होने की प्रायिकता क्या है?
उत्तर:E_{1} =A मशीन द्वारा खराब बोल्ट का उत्पादन,P\left ( E_{1} \right )=0.25
E_{2} =B मशीन द्वारा खराब बोल्ट का उत्पादन,P\left ( E_{2} \right )=0.35
E_{3} =C मशीन द्वारा खराब बोल्ट का उत्पादन,P\left ( E_{3} \right )=0.40
A=बोल्ट के खराब होने की घटना
P\left(\frac{A}{E_{1}}\right)=0.05, P\left(\frac{A}{E_{2}}\right)=0.04, P\left(\frac{A}{E_{3}} \right)=0.02 \\P\left(\frac{E_{1}}{A}\right)=\frac{P\left(E_{1}\right) \cdot P\left(\frac{A}{E_{1}} \right)}{P\left(E_{1}\right) \cdot P\left(\frac{A}{E_{1}}\right)+P\left(E_{2}\right) \cdot P\left( \frac{A}{E_{2}}\right)+P\left(E_{3}\right) \cdot P\left(\frac{A}{E_{3}}\right)}\\ =\frac{0.25 \times 0.05}{0.25 \times 0.05+0.35 \times 0.04+0.40 \times 0.02} \\ =\frac{125}{125+140+80} =\frac{125}{345}=\frac{25}{69}
प्रश्न:3.थैले A में 2 सफेद और 3 लाल गेंदें हैं और थैले B में 4 सफेद और 5 लाल गेंदें है।किसी एक थैले में से यदृच्छया एक गेंद निकाली गई और पाया गया कि यह लाल रंग की गेंद है तो दूसरे थैले से निकाले जाने की प्रायिकता ज्ञात कीजिए।
उत्तर:पहला थैला चुनने की घटना=E_{1}
दूसरा थैला चुनने की घटना=E_{2}
A=लाल गेंद निकालने की घटना
P\left(E_{1}\right)=P\left(E_{2}\right)=\frac{1}{2}, P\left(\frac{A}{E_{1}}\right)=\frac{3}{5}, P\left(\frac{A}{E_{2}}\right)=\frac{5}{9} \\ P\left(\frac{E_{2}}{A}\right)=\frac{P\left(E_{2}\right) \cdot P\left(\frac{A}{E_{2}}\right)}{P\left(E_{1}\right) \cdot P\left(\frac{A}{E_{1}}\right)+ P\left(E_{2} \right) \cdot P \left ( \frac{A}{E_{2}} \right )} \\ =\frac{\frac{1}{2} \times \frac{5}{9}}{\frac{1}{2} \times \frac{3}{5}+\frac{1}{2} \times \frac{5}{9}} \\= \frac{\frac{1}{2} \times \frac{5}{9}}{\frac{1}{2} \times \frac{3}{5}+\frac{1}{2} \times \frac{5}{9}} \\ =\frac{\frac{5}{18}}{\frac{3}{10}+\frac{5}{8}}=\frac{\frac{5}{18}}{27+25} \\ =\frac{5}{18} \times \frac{90}{52}=\frac{25}{52}
उपर्युक्त प्रश्नों के उत्तर द्वारा सम्पूर्ण प्रायिकता का प्रमेय (Theorem of Total Probability),बेज प्रमेय (Baye’s Theorem) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
Theorem of Total Probability
सम्पूर्ण प्रायिकता का प्रमेय
(Theorem of Total Probability)
Theorem of Total Probability
सम्पूर्ण प्रायिकता का प्रमेय (Theorem of Total Probability):(1.)एक प्रतिदर्श समष्टि का विभाजन
(Partition of a Sample Space):