Permutation and Combination
1.क्रमचय और संचय (Permutation and Combination),क्रमचय (Permutations):
क्रमचय और संचय (Permutation and Combination):
क्रमचय (Permutation):दी हुई वस्तुओं में से कुछ अथवा सभी को एक साथ लेकर उन्हें जितने भिन्न-भिन्न क्रमों या विन्यासों (arrangements) में रखा जा सकता है,उनमें से प्रत्येक को क्रमचय कहते हैं।
गुणन का आधारभूत सिद्धांत (Fundamental Principle of Multiplication): माना की कोई घटना A,m प्रकार से और घटना B,n प्रकार से घटित हो सकती है एवं माना कि घटना A और B आपस में संबंधित नहीं है। अर्थात् घटना B का n प्रकार घटित होना घटना A के परिणाम पर निर्भर नहीं है।तब दोनों घटनाएं A और B संयुक्त रूप से प्रकार से m×n प्रकार से घटित हो सकती हैं।
योग का आधारभूत सिद्धांत (Fundamental Principle of Addition):माना की कोई घटना A,m प्रकार से और घटना B,n प्रकार से घटित हो सकती है जबकि दोनों घटनाएं एक साथ घटित नहीं हो सकती हैं।तब घटना A या B (दोनों में से कम से कम एक) (m+n) प्रकार से घटित हो सकती हैं।
क्रमगुणित (Factorial):प्रथम n प्राकृत संख्याओं के गुणनफल को क्रमगुणित n कहते हैं एवं इसे n! या \lfloor n द्वारा प्रदर्शित किया जाता है।अर्थात् n!=1.2.3.4……..(n-1).n
इसी प्रकार 3!=1.2.3,4!=1.2.3.4=24,5!=1.2.3.4.5=120 इत्यादि।
n!=1.2.3.4………(n-1)n
=[1.2.3…….(n-1)].n=(n-1)!n
इस प्रकार n!=n (n-1)!
क्रमचयों की संख्या (Number of Permutations):
प्रमेय (Theorem):1.n विभिन्न वस्तुओं में से एक साथ r वस्तुओं के चयन के क्रमचयों की संख्या:
n (n-1) (n-2) (n-3)………{n-(r-1)}
अर्थात् ^{n}P_{r}=n(n-1).(n-2) \cdots(n-r+1)
प्रमाण (Proof):माना कि हमारे पास कुल n विभिन्न वस्तुएं हैं और हमें r स्थानों को भरना है।पहले स्थान के लिए n वस्तुओं में से किसी भी एक वस्तु को चुना जा सकता है।अतः पहले स्थान के लिए वस्तु को चुनने की विधियां n है। अब दूसरे स्थान के लिए (n-1) वस्तुओं में से ही चुनना होगा।अतः दूसरे स्थान के लिए वस्तु को चुनने की विधियां (n-1) है।फलतः गुणन के आधारभूत सिद्धांत से पहले दो स्थान n (n-1) विधियों से भरे जा सकते हैं।इन दो स्थानों के भरने के बाद तीसरे स्थान के लिए शेष (n-2) वस्तुओं में से चुनना होगा।अतः तीसरे स्थान के लिए वस्तुओं को चुनने की विधियां (n-2)हैं।इसलिए पहले तीन स्थान n (n-1) (n-2) से भरे जा सकते हैं।इसी प्रकार से इस क्रिया को आगे बढ़ाते हुए बढ़ाते हुए r स्थानों को भरने की विधियां n (n-1) (n-2)………{n-(r-1)} होंगी।इस संख्या को से व्यक्त करते हैं।अतः n विभिन्न वस्तुओं में से एक साथ r वस्तुओं के चयन के क्रमचयों की संख्या है:
^{n}P_{r}=n(n-1).(n-2) \cdots(n-r+1)
उन वस्तुओं के क्रमचय जिनमें सभी भिन्न नहीं हों (Permutations of those objects in which not all distinct):
प्रमेय (Theorem):2.माना की n वस्तुएं जिनमें p वस्तुएं एक प्रकार की ,q वस्तुएं दूसरे प्रकार की,r वस्तुएं तीसरे प्रकार की व शेष भिन्न-भिन्न हों तो सभी को एक साथ लेकर बनाए जाने वाले क्रमचयों की संख्या होगी
\frac{n!}{p!q!r!}
प्रमाण (Proof):माना के हमारे पास कुल n वस्तुएं हैं।उनमें से p एक प्रकार की,q दूसरे प्रकार की,r तीसरे प्रकार की व शेष भिन्न-भिन्न हैं।माना कि अभीष्ट क्रमचयों की संख्या x है।यदि इन क्रमचयों में से एक क्रमचय लें और यदि p समान वस्तुओं को p असमान वस्तुओं से बदल दें तो अब p! नए क्रमचय बनेंगे।
इसी प्रकार क्रमश: q तथा r वस्तुओं को q तथा r असमान वस्तुओं से बदल दें तो अब q! तथा r! नए क्रमचय बनेंगे। इस प्रकार यदि उपर्युक्त प्रतिस्थापन एक साथ किए जाएं तो हमें प्रत्येक क्रमचय से p!×q!×r! क्रमचय प्राप्त होंगे।
अब क्योंकि वस्तुएं भिन्न हो गई है और सभी को एक साथ लेकर बनाए जाने वाले क्रमचयों की संख्या n! है अतः
x \times p! \times q! \times r!=n! \\ \therefore x=\frac{n!}{p!q!r!}
वृत्तीय क्रमचय (Circular Permutations):अभी तक हमने वस्तुओं के एक पंक्ति में क्रमचयों के बारे में अध्ययन किया है।इस तरह के क्रमचयों को वृत्तीय (चक्रीय) क्रमचय कहते हैं।प्रत्येक रैखिक क्रमचय में किसी एक वस्तु को स्थिर मानकर शेष वस्तुओं को रैखिक क्रमचय की तरह व्यवस्थित करते हैं।
प्रमेय (Theorem):3.n विभिन्न वस्तुओं के वृत्तीय क्रमचयों की संख्या (n-1)! होती है।
प्रमाण (Proof):वृत्तीय क्रमचय में कोई सिरा नहीं होता है इसलिए वृत्तीय क्रमचय में हमें केवल वस्तुओं की सापेक्ष स्थिति पर ध्यान देना पड़ता है।मानाकि हमें n वस्तुओं को एक वृत्त के आकार (जैसे गोल मेज इत्यादि) में व्यवस्थित करना है।n वस्तुओं में से सर्वप्रथम एक वस्तु लेकर उसे एक निश्चित स्थान पर रखते हैं।फिर शेष (n-1) वस्तुओं को इस वस्तु के सापेक्ष (n-1)! विधियों से व्यवस्थित कर सकते हैं।
अतः n वस्तुओं को एक साथ लेने पर वृत्तीय क्रमचयों की संख्या (n-1)! होगी।
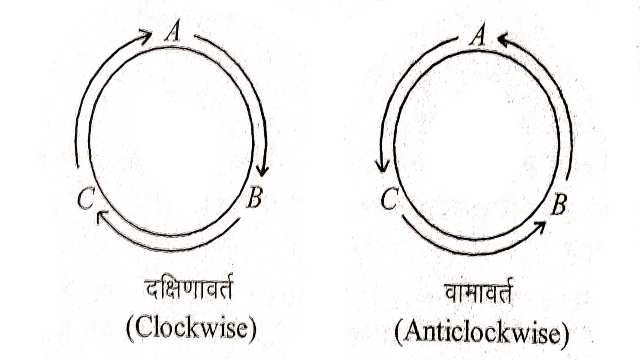
दक्षिणावर्त तथा वामावर्त क्रमचयों में अन्तर (Difference between clockwise and anticlockwise Permutations):
A,B,C अक्षरों के निम्नलिखित 6 क्रमचय बनते हैंः
ABC,ACB,BAC,BCA,CAB,CBA
(1.)ABC,BCA,CAB के अवयवों का एक ही क्रम (दक्षिणावर्त क्रम) है।अतः इन तीन रैखिक क्रमचयों को चक्रीय क्रमचयों में एक ही क्रमचय माना जाता है।
(2.)ACB,CBA,BAC के अवयवों का एक ही क्रम(वामावर्त क्रम) है।अतः इन तीन रैखिक क्रमचयों को चक्रीय क्रमचयों में एक ही क्रमचय माना माना जाता है।
अतः A,B,C अक्षरों के कुल चक्रीय क्रमचयों की संख्या 2 है।यदि दक्षिणावर्त एवं वामावर्त चक्रीय क्रमचयों में कोई अंतर नहीं माना जाए तो A,B,C अक्षरों के कुल चक्रीय क्रमचयों की संख्या 1 है।अतः यदि दक्षिणावर्त तथा वामावर्त क्रमचयों को एक ही समझा जाए तो n विभिन्न वस्तुओं में से सभी वस्तुएं एक साथ लेकर बनाए जाने वाले क्रमचयों की संख्या \frac{(n-1)!}{2} होगी।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Complex Numbers
2.क्रमचय और संचय के उदाहरण (Permutation and Combination Examples):
n का मान ज्ञात कीजिए जबकि
Example:1.^{(n-1)}P_{3} :^{(n+1)}P_{3}=5:12
Solution:\frac{(n-1)!}{(n-4)!} :\frac{(n+1)!}{(n-2)!}=5:12 \\ \Rightarrow \frac{(n-1)(n-2)(n-3)(n-4) !}{(n-4) !} : \frac{(n+1) n(n-1)(n-2) !}{(n-2) !}=5: 12 \\ \Rightarrow(n-1)(n-2)(n-3):(n+1)(n)(n-1)=5 : 12 \\ \Rightarrow \frac{(n-2)(n-3)}{n(n+1)}= \frac{5}{12} \\ \Rightarrow 12\left(n^{2}-5 n+6\right)= 5\left(n^{2}+n\right) \\ \Rightarrow 12 n^{2}-60 n+72=5 n^{2}+5 n \\ \Rightarrow 7 n^{2}-65 n+72=0 \\ \Rightarrow 7 n^{2}-56 n-9 n+72=0 \\ \Rightarrow 7 n(n-8)-9(n-8)=0 \\ \Rightarrow(n-8)(7 n-9)=0
n का मान धनात्मक पूर्णांक होता है अतः n=8
Example:2.^n P_{6} =10 . ^nP_{5}
Solution:^n P_{6} =10 . ^nP_{5} \\\frac{n !}{(n-6) !} =\frac{10 \cdot(n !)}{(n-5) !} \\ \Rightarrow \frac{1}{(n-6) !} =\frac{10}{(n-5)(n-6)!} \\ \Rightarrow \frac{1}{1}=\frac{10}{n-5} \\ \Rightarrow n-5 =10 \\ \Rightarrow n =15
Example:3.^{56} P_{n+6}: ^{54} P_{n+3}=30800
Solution:^{56} P_{n+6}: ^{54} P_{n+3}=30800 \\ \Rightarrow \frac{56 !}{(50-n) !} : \frac{54 !}{(51-n) !}=30800 \\ \Rightarrow \frac{(56)(55) 54 !}{(50-n) !} : \frac{54!}{(51-n)(50-n) !}=30800 \\ \Rightarrow(56)(55): \frac{1}{(51-n)}=30800 \\ \Rightarrow(51-n)(56)(55)=30800 \\ \Rightarrow 51-n=10 \\ \Rightarrow n=41
Example:4.^{6+n} P_{2}: ^{6-n} P_{2}=56: 12
Solution:^{6+n} P_{2}: ^{6-n} P_{2}=56: 12 \\ \Rightarrow \frac{(6+n)!}{(4+n)!}:\frac{(6-n)!}{(4-n)!} =56: 12 \\ \Rightarrow \frac{(6+n)(5+n)(4+n)!}{(4+n)!}:\frac{(6-n)(5-n)(4-n)!}{(4-n)!} =56: 12 \\ \Rightarrow(6+n)(5+n) :(6-n) (5-n)=14: 3 \\ \Rightarrow 3\left(30+11 n + n^{2}\right)=14\left(30-11 n+n^{2}\right) \\ \Rightarrow 3 n^{2}+33 n+90=420-154 n+14 n^{2} \\ \Rightarrow 11 n^{2}-187 n+330=0 \\ \Rightarrow n^{2}-17 n+30=0 \\ \Rightarrow n^{2}-15 n-2 n+30=0 \\ \Rightarrow n(n-15)-2(n-15)=0 \\ \Rightarrow (n-15)(n-2)=0 \\ \Rightarrow n=15
n=15 असंभव है।अतः n=2
Example:5.ALLAHABAD शब्द के अक्षरों से विभिन्न शब्दों की संख्या ज्ञात कीजिए।
Solution:ALLAHABAD में कुल अक्षर हैं जिनमें A चार,L दो तथा H,B,D एक-एक हैं।अतः क्रमचयों की अभीष्ट संख्या
=\frac{9!}{4 ! 2 !}=\frac{9 \times 8 \times 7 \times 6 \times 5 \times 4!}{4 ! \times 2 \times 1} \\ =\frac{9 \times 8 \times 7 \times 6 \times 5}{2}=9 \times 8 \times 7 \times 3 \times 5=7560
Example:6.TRIANGLE शब्द के अक्षरों से कितने शब्द बनाए जा सकते हैं?इनमें से कितने शब्द से T आरम्भ और E पर समाप्त होते हैं?
Solution:TRIANGLE शब्द के अक्षरों से बनने वाले कुल शब्द=3!
=8×7×6×5×4×3×2×1=40320
T से आरंभ और E से समाप्त होने वाले शब्दों में T व E तो अपरिवर्तनीय स्थिति में होंगे।अत: शेष 6 अक्षरों से ही शब्द बनेंगे।अतः बनने वाले शब्दों की अभीष्ट संख्या=6!=6×5×4×3×2×1=720
Example:7.अंकों 1,2,3,4,5,6 से 3000 तथा 4000 के मध्य ऐसी कितनी संख्याएं बनाई जा सकती है,जो 5 से विभाज्य है।
Solution:3000 से 4000 के बीच प्रत्येक संख्या चार अंको की होगी।प्रत्येक संख्या 3 से शुरू होगी।इन संख्याओं के से 5 से विभाजित होने की स्थिति में अंतिम अंक (इकाई) 0 या 5 होगा।अतः 1,2,3,4,5,6 के प्रयोग में 3 तथा 5 तो शुरू व अंत में आएंगे।शेष चार अंकों के दो स्थान भरने हैं।अतः अभीष्ट संख्याओं की संख्या=^4 P_{2}=\frac{4 !}{2!}=12
Example:8.अंकों 0,1,2,3,4,5.से. छ: अंकों की कितनी संख्याएं बनाई जा सकती है?
Solution:0,1,2,3,4,5 अंकों को लेकर छ: अंकों की 6! प्रकार की संख्याएं बनाई जा सकती है परन्तु जिनके शुरू में 0 होगा वे छ: अंकों की बजाय पाँच अंकों की ही संख्याएं होंगी।अतः वास्तविक छ: अंकों की अभीष्ट संख्याएं=6!-5!=720-120=600
Example:9.अंकों 1,2,3,4,5,6 से 1000 से छोटी कितनी संख्याएं बनाई जा सकती है जबकि अंकों की पुनरावृत्ति न हो।
Solution:1000से छोटी क्रमशः एक अंक की,दो अंकों की तथा तीन अंकों संख्याएं होती हैं।
अत: (1.)1 अंक की संख्याओं की संख्या=^6 P_{1}=6
(2.)2 अंकों की संख्याओं की संख्या=^6 P_{2}=6 \times 5=30
(3.)3अंकों की संख्याओं की संख्या=^6P_{3}=6 \times 5 \times 4=120
अतः कुल अभीष्ट संख्याएं=6+30+120=156
Example:10.एक समिति के 15 सदस्य एक गोल मेज के चारों ओर कितने प्रकार से बैठ सकते हैं जबकि सचिव,अध्यक्ष के एक ओर तथा उप सचिव दूसरी ओर बढ़ता है।
Solution:15 सदस्यों में अध्यक्ष,सचिव,उपसचिव तीनों के लिए केवल निम्न स्थिति संभव है :
सचिव अध्यक्ष उपसचिव
उपसचिव अध्यक्ष सचिव
अतः तीनों को एक मानने पर एवं सचिव व उपसचिव को दोनों तरफ व्यवस्थित करने की स्थिति में अभीष्ट संख्या=12!×2!
Example:11.एक रेलवे लाईन पर 15 स्टेशन हैं।इसके लिए एक श्रेणी के विभिन्न प्रकार के कितने टिकट छपवाने चाहिए कि किसी स्टेशन से एक व्यक्ति इस लाईन के किसी भी अन्य स्टेशन का टिकट खरीद सके?
Solution:किसी भी एक स्टेशन पर अन्य कुल 14 स्टेशनों के टिकट उपलब्ध होने चाहिए अर्थात् सभी 15 स्टेशनों में से प्रत्येक पर अन्य 14 स्टेशनों के टिकट उपलब्ध होने चाहिए।अतः अभीष्ट संख्या=15×14=120
Example:12.शब्द SCHOOL के अक्षरों से कितने शब्द बनाएं जा सकते हैं जबकि दोनों O साथ नहीं आते हों।
Solution:SCHOOL शब्द के अक्षरों से बनने वाले कुल क्रमचय=\frac{6!}{2!}=360
दोनों O के साथ आने पर बनने वाले शब्दों की संख्या=5!=120
अतः दोनों के O साथ-साथ नहीं आने पर बनने वाले शब्द के शब्दों की संख्या=360-120=240
उपर्युक्त उदाहरणों के द्वारा क्रमचय और संचय (Permutation and Combination),क्रमचय (Permutations) को समझ सकते हैं।
3.क्रमचय और संचय की समस्याएं (Permutation and Combination Problems):
(1.) MATHEMATICS शब्द के अक्षरों से विभिन्न शब्दों की संख्या ज्ञात कीजिए।
(2.)7 व्यक्ति एक गोल मेज के चारों ओर कितने प्रकार से बैठ सकते हैं सकते हैं?
(3.)7 विभिन्न मोती एक छल्ले में कितने प्रकार से पिरोए जा सकते हैं?
(4.)10 व्यक्ति गोल मेज के चारों ओर कितने प्रकार से बैठ सकते हैं जबकि सदैव एक से पड़ौसी न होंगे?
उत्तर (Answers): (1)\frac{11!}{2!2!2!} \\(2)720 \\(3)360 \\ (4)\frac{9!}{2}
उपर्युक्त सवालों को हल करने पर क्रमचय और संचय (Permutation and Combination),क्रमचय (Permutations) को ठीक से समझ सकते हैं।
Also Read This Article:-Equation of Straight Line
4.क्रमचय और संचय (Permutation and Combination),क्रमचय (Permutations) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.आप क्रमचय की गणना कैसे करते हैं? (How do you calculate permutations?):
उत्तर:क्रमचय की संख्या की गणना करने के लिए,प्रत्येक घटना के लिए संभावनाओं की संख्या लें और फिर उस संख्या को X बार गुणा करें,जहां X अनुक्रम में घटनाओं की संख्या के बराबर है।उदाहरण के लिए,चार अंकों के पिन के साथ,प्रत्येक अंक 0 से 9 तक हो सकता है,जिससे हमें प्रत्येक अंक के लिए 10 संभावनाएं मिलती हैं।
गणित में,एक समुच्चय का क्रमचय,शिथिल रूप से,उसके सदस्यों की एक क्रम या रैखिक क्रम में व्यवस्था (arrangement) है या यदि समुच्चय पहले से ही क्रमित (already ordered) है,तो उसके तत्वों का पुनर्व्यवस्थापन (rearrangement) है।शब्द “क्रमचय”एक क्रमित सेट (ordered set) के रैखिक क्रम को बदलने की क्रिया या प्रक्रिया को भी संदर्भित करता है।
प्रश्न:2.संचय और क्रमचय के बीच अंतर क्या है? (What is difference between combination and permutation?):
उत्तर:गणितीय अवधारणाओं के संदर्भ में,”क्रमचय”और “संचय” एक दूसरे से संबंधित हैं।संचय उन चयनों की गिनती है जो हम n वस्तुओं से करते हैं।जबकि क्रमचय n वस्तुओं से व्यवस्थाओं (arrangements) की संख्या की गणना कर रहा है।
प्रश्न:3.क्रमचय नियम क्या है? (What is the permutation rule?):
उत्तर:विशेष क्रमचय नियम में कहा गया है कि कुछ भी क्रमचय अपने आप में क्रमगुणित (Factorial) के बराबर है।उदाहरण: (3) 2 = 3!
टिप्पणी: संचय और क्रमचय के बीच का अंतर यह है कि संचय के लिए वस्तुओं का क्रम महत्वपूर्ण नहीं है।
प्रश्न:4.क्रमचय में N और R का क्या अर्थ है? (What does N and R stand for in permutations?):
उत्तर:n= सेट में कुल आइटम (total items in the set); r=क्रमचय के लिए ली गई वस्तुएँ (items taken for the permutation);”!” फैक्टोरियल को दर्शाता है।
प्रश्न:5.आप वास्तविक जीवन में क्रमचय और संचय का उपयोग कैसे करते हैं? (How do you use permutations and combinations in real life?),क्रमचय और संचय के वास्तविक जीवन के उदाहरण क्या हैं? (What are the real-life examples of permutations and combinations?):
उत्तर:लोगों (people),अंकों (digits),संख्याओं (numbers),अक्षरों (alphabets),अक्षरों (letters) और रंगों (colours) को व्यवस्थित करना क्रमचय के उदाहरण हैं।मेनू (menu),भोजन (food),कपड़े (clothes),विषय(subjects),टीम (team) का चयन संचय के उदाहरण हैं।
प्रश्न:6.क्रमचय कितने प्रकार के होते हैं? (What are the types of permutation?):
उत्तर:क्रमचय को तीन अलग-अलग श्रेणियों में वर्गीकृत किया जा सकता है:
n विभिन्न वस्तुओं का क्रमचय (जब दोहराव की अनुमति नहीं है)
दोहराव (Repetition),जहां दोहराव की अनुमति है।
क्रमचय जब वस्तुएं भिन्न-भिन्न नहीं होती हैं (बहु सेटों का क्रमचय)
प्रश्न:7.क्रमचय का उपयोग कहाँ किया जाता है? (Where is permutation used?):
उत्तर:गणित की लगभग हर शाखा में और विज्ञान के कई अन्य क्षेत्रों में क्रमचय का उपयोग किया जाता है।कंप्यूटर विज्ञान में,उनका उपयोग सॉर्टिंग एल्गोरिदम का विश्लेषण करने के लिए किया जाता है;क्वांटम भौतिकी में,कणों की अवस्थाओं का वर्णन करने के लिए;और जीव विज्ञान में, आरएनए (RNA) अनुक्रमों का वर्णन करने के लिए।
प्रश्न:8.आप दोहराव के बिना क्रमचय कैसे करते हैं? (How do you do permutations without repetition?):
उत्तर:दोहराव के बिना संचय (Combinations without Repetition)
संख्याएँ एक बार में एक खींची जाती हैं और यदि हमारे पास भाग्यशाली संख्याएँ हैं (चाहे कोई भी क्रम हो) तो हम जीत जाते हैं!इसे समझाने का सबसे आसान तरीका यह है कि: मान लें कि ऑर्डर मायने रखता है (यानी क्रमचय), फिर इसे बदल दें ताकि ऑर्डर कोई फर्क न पड़े।
प्रश्न:9.आप कैसे जानते हैं कि क्रमचय या संचय का उपयोग कब करना है? (How do you know when to use permutation or combination?):
उत्तर:इसलिए,क्रमचय का उपयोग सूचियों (lists) (क्रम का महत्त्व) और समूहों (groups) के लिए संचय (क्रम कोई फर्क नहीं पड़ता) के लिए किया जाता है।अंतर के लिए प्रसिद्ध मजाक है: “संचय लॉक” को वास्तव में “क्रमचय लॉक” कहा जाना चाहिए।
प्रश्न:10.क्या वास्तविक जीवन में क्रमचय सीखना महत्वपूर्ण है? (Is learning permutation important in real life?):
उत्तर: क्रमचय विभिन्न प्रकार की गणना समस्याओं में महत्वपूर्ण हैं (विशेषकर वे जिनमें क्रम महत्वपूर्ण है),साथ ही साथ गणित के विभिन्न अन्य क्षेत्रों में;उदाहरण के लिए, सारणिक (determinant) को अक्सर क्रमचय का उपयोग करके परिभाषित किया जाता है।
प्रश्न:11.संचय या क्रमचय स्थितियों की पहचान करने के लिए कीवर्ड क्या हैं? (What are the keywords to identify a combination or permutation situations?):
उत्तर:चयन (selection),चुनना (choose),चयन (pick) और संयोजन (combination) जैसे खोज शब्दों से संकेत मिलता है कि यह एक संचय प्रश्न है।कीवर्ड जैसे-व्यवस्था (arrangement),क्रमित (ordered),अद्वितीय (unique)- इंगित करता है कि यह एक क्रमचय प्रश्न है।
प्रश्न:12.आप अद्वितीय क्रमचय की गणना कैसे करते हैं? (How do you calculate unique permutations?):
उत्तर:कैसे करें: n विशिष्ट विकल्पों को देखते हुए,निर्धारित करें कि कितने क्रमचय हैं।
निर्धारित करें कि पहली स्थिति के लिए कितने विकल्प हैं।
निर्धारित करें कि दूसरी स्थिति के लिए कितने विकल्प बचे हैं।
तब तक जारी रखें जब तक कि सभी धब्बे भर न जाएं।
संख्याओं को एक साथ गुणा करें।
प्रश्न:13.आपको कैसे पता चलेगा कि किसी समस्या में क्रमचय शामिल है? (How would you know if a problem involves permutation?):
उत्तर:एक प्रश्न को क्रमचय के रूप में पहचाना या निर्धारित किया जा सकता है यदि प्रश्न किसी सेट की किसी अन्य विशेष अनुक्रम या पुनर्व्यवस्था (particular sequence or rearrangement) में निश्चित व्यवस्था (certain arrangement) के लिए कहता है।प्रश्न की प्रकृति के कारण इस अवधारणा को कभी-कभी संचय के प्रकार के रूप में गलत समझा जा सकता है।
प्रश्न:14.क्रमचय और संचय की समानताएं क्या हैं? (What is the similarities of permutation and combination?):
उत्तर:”क्रमचय” और “संचय” संबंधित गणितीय अवधारणाएं हैं।”संचय” एक मानदंड या श्रेणी के भीतर मूल्यों का कोई चयन या जोड़ी है (selection or pairing of values within a single criteria or category) जबकि “क्रमचय” एक क्रमित संचय (ordered combination) है।2.संचय ऑर्डर,प्लेसमेंट या व्यवस्था (arrangement) पर नहीं बल्कि पसंद पर जोर (emphasis) देते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा क्रमचय और संचय (Permutation and Combination),क्रमचय (Permutations) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा क्रमचय और संचय (Permutation and Combination),क्रमचय (Permutations) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
