General Equation of Line Class 11
1.रेखा का व्यापक समीकरण कक्षा 11 (General Equation of Line Class 11),गणित में रेखा का व्यापक समीकरण (General Equation of Line Class 11 in Mathematics):
रेखा का व्यापक समीकरण कक्षा 11 (General Equation of Line Class 11) Ax+By+C=0 का लेखाचित्र सदैव एक सरल रेखा होता है।इसलिए जब A और B एक साथ शून्य नहीं हैं तो Ax+By+C=0 के रूप का कोई समीकरण रेखा का व्यापक समीकरण (General Equation) कहलाता है।
Ax+By+C=0 के विभिन्न रूप (Different Forms of Ax+By+C=0):
समीकरण को विभिन्न प्रक्रियाओं द्वारा रेखा के समीकरण के विभिन्न रूपों में रूपान्तरित किया जा सकता है।
(1.)ढाल-अन्तःखण्ड रूप (Slope-Intercept form):
यदि B \neq 0 तो Ax+By+C=0 को y=-\frac{A}{B} x-\frac{C}{B} या y=mx+c…….(1)
जहाँ m=-\frac{A}{B} और c=-\frac{C}{B} के रूप में लिखा जा सकता है।
समीकरण (1) उस रेखा की ढाल-अन्तःखण्ड रूप है जिसकी ढाल -\frac{A}{B} और y अन्तः खण्ड -\frac{C}{B} है।यदि B=0 तो x=-\frac{C}{A} जो कि एक उर्ध्वाधर रेखा का समीकरण है जिसकी ढाल अपरिभाषित और x-अन्तःखण्ड -\frac{C}{A} है।
(2.)अन्तःखण्ड रूप (Intercept Form):
यदि C \neq 0 तो Ax+By+C=0 को
\frac{x}{-\frac{C}{A}}+\frac{y}{-\frac{C}{B}}=1 या \frac{x}{a}+\frac{y}{b}=1 \cdots(1)
जहाँ a=-\frac{C}{A} और b=-\frac{C}{B}
समीकरण (1) उस रेखा के समीकरण का अन्तःखण्ड रूप है जिसके क्रमशः x-अन्तःखण्ड -\frac{C}{A} और y-अन्तःखण्ड -\frac{C}{B} हैं।
यदि C=0 तो Ax+By+C=0 को Ax+By=0 लिखा जा सकता है जो मूलबिन्दु से जानेवाली रेखा है इसलिए अक्षों पर शून्य अन्तःखण्ड है।
(3.)लम्ब रूप (Normal Form):
मान लीजिए कि समीकरण Ax+By+C=0 या Ax+By=-C से निरूपित रेखा का लम्ब रूप x \cos \omega+y \sin \omega=p है,जहाँ p मूलबिन्दु से रेखा पर डाले गए लम्ब की लम्बाई है और लम्ब एवं x-अक्ष की धनात्मक दिशा के बीच का कोण है इसलिए दोनों समीकरण समान हैं अतः
\frac{A}{\cos \omega}=\frac{B}{\sin \omega}=-\frac{C}{p} \cdots(1)
जिससे \cos \omega=-\frac{A p}{C} और \sin \omega=-\frac{B p}{C} प्राप्त होता है।
अब \sin^2 \omega+\cos ^2 w=\left(-\frac{A p}{C}\right)^2+\left(\frac{-B p}{C}\right)^2=1
अथवा p^2=\frac{C^{2}}{A^2+B^2} या p=\pm \frac{C}{\sqrt{A^2+B^2}}
इसलिए \cos \omega=\pm \frac{A}{\sqrt{A^2+B^2}} और \sin \omega=\pm \frac{B}{\sqrt{A^2+B^2}}
इस प्रकार समीकरण Ax+By+C=0 का लम्ब रूप
x \cos \omega+y \sin \omega=p जहाँ \cos \omega=\pm \frac{A}{\sqrt{A^2+B^2}} , \sin \omega=\pm \frac{B}{\sqrt{A^2+B^2}} और p=\pm \frac{C}{\sqrt{A^2+B^2}} हैं।
चिन्हों का उचित चयन इस प्रकार किया जाता है कि p धनात्मक रहे।
एक बिन्दु की रेखा से दूरी (Distance of a Point From a Line):
एक बिन्दु की किसी रेखा से दूरी बिन्दु से रेखा पर डाले गए लम्ब की लम्बाई है।मान लीजिए कि L:Ax+By+C=0 एक रेखा है,जिसकी बिन्दु \left ( x_{1},y_{1} \right ) से दूरी d है।बिन्दु P से रेखा पर लम्ब PL खींचिए (आकृति)।यदि रेखा x-अक्ष और y-अक्ष को क्रमशः Q और R पर मिलती है तो इन बिन्दुओं के निर्देशांक Q\left(-\frac{C}{A}, 0\right) और R\left(0,-\frac{C}{B}\right) हैं।
त्रिभुज PQR का क्षेत्रफल
निम्नलिखित प्रकार से किया जा सकता हैः
क्षेत्रफल (\triangle P Q R)=\frac{1}{2} \text{PM} \cdot \text{QR} जिससे PM=\frac{2 \text{ क्षेत्रफल } \triangle PQR}{QR} \cdots(1)
साथ ही \triangle PQR का क्षेत्रफल=\frac{1}{2}\left|x_1 \left(0+\frac{C}{B}\right)+\left(-\frac{C}{A}\right)\left(-\frac{C}{B}-y_{1} \right)+0\left ( y_{1} -0 \right ) \right| \\ =\frac{1}{2}\left|x_1 \frac{C}{B}+y_{1} \frac{C}{A}+\frac{C^2}{A B}\right| या 2 \triangle PQR का क्षेत्रफल=\left|\frac{C}{A B}\right| \cdot\left|A x_1+B y_{1}+C\right|
और QR=\sqrt{\left(0+\frac{C}{A}\right)^2+\left(\frac{C}{B}-0\right)^2}=\left|\frac{C}{A B}\right| \sqrt{A^2+B^2}
\triangle PQR के क्षेत्रफल और QR के मान (1) में रखने परः
PM=\frac{\left|A x_1+B y_1+C\right|}{\sqrt{A^2+B^2}} \\ \Rightarrow d=\frac{\left|A x_1+B y_1+C\right|}{\sqrt{A^2+B^2}}
इस प्रकार बिन्दु \left ( x_{1},y_{1} \right ) से रेखा Ax+By+C=0 की लाम्बिक दूरी (d) इस प्रकार हैः
d=\frac{\left|A x_1+B y_1+C\right|}{\sqrt{A^2+B^2}}
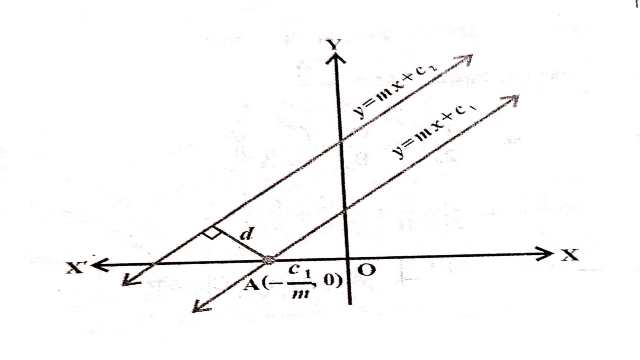
दो समान्तर रेखाओं के बीच दूरी (Distance Between Two Parallel Lines):
हम जानते हैं कि समान्तर रेखाओं की ढाल समान होते हैं।इसलिए,समान्तर रेखाएँ इस रूप में लिखी जा सकती हैंः
y=m x+c_1 \cdots (1)
और y=m x+c_2 \cdots (2)
रेखा (1) x-अक्ष पर बिन्दु A\left ( -\frac{C_{1}}{m},0 \right ) में प्रतिच्छेद करेगी जैसा आकृति में दिखाया गया है।दो रेखाओं के बीच की दूरी,बिन्दु A से रेखा (2) पर लम्ब की लम्बाई है।इसलिए,रेखाओं (1) और (2) के बीच की दूरी
\frac{\left|(-m)\left(-\frac{c_1}{m}\right)+\left(-c_2\right)\right|}{\sqrt{1+m^2}} या d=\frac{\left|c_1-c_2\right|}{\sqrt{1+m^2}} है।
इस प्रकार दो समान्तर रेखाओं y=m x+c_{1} और y=m x+c_{2} के बीच की दूरी d=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{1+m^2}}
यदि रेखाएँ व्यापक रूप में दी गई हैं अर्थात् A x+B y+C_{1}=0 और A x+B y+C_{2}=0
उपर्युक्त सूत्र d=\frac{\left|C_1-C_2\right|}{A^2+B^2} का रूप ले लेता है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Straight Line Class 11
2.रेखा का व्यापक समीकरण कक्षा 11 पर आधारित उदाहरण (Examples Based on General Equation of Line Class 11):
Example:1.निम्नलिखित समीकरणों को ढाल अन्तःखण्ड रूप में रूपान्तरित कीजिए और उनके ढाल तथा y-अन्तः खण्ड ज्ञात कीजिएः
Example:1(i).x+7y=0
Solution:x+7y=0
y=-\frac{x}{7}+0
ढाल=-\frac{1}{7}, y-अन्तःखण्ड=0
Example:1(ii).6x+3y-5=0
Solution:6x+3y-5=0
y=-\frac{6 x}{3}-\frac{5}{3}\\ \Rightarrow y=-2 x-\frac{5}{3}
ढाल=-2,y-अन्तःखण्ड=-\frac{5}{3}
Example:1(iii).y=0
Solution:y=0
y=0.x+0
ढाल=0,y-अन्तःखण्ड=0
Example:2.निम्नलिखित समीकरणों को अन्तःखण्ड रूप में रूपान्तरित कीजिए और अक्षों पर इनके द्वारा काटे गए अन्तःखण्ड ज्ञात कीजिएः
Example:2(i).3x+2y-12=0
Solution: 3 x+2 y-12=0 \\ \Rightarrow 3 x+2 y=12 \\ \Rightarrow \frac{3 x}{12}+\frac{2}{12} y=1 \\ \Rightarrow \frac{x}{4}+\frac{y}{6}=1
अन्तःखण्ड
a=4,b=6
Example:2(ii).4x-3y=6
Solution:4 x-3 y=6 \\ \Rightarrow \frac{4 x}{6}-\frac{3 y}{6}=1 \\ \Rightarrow \frac{x}{\frac{3}{2}}-\frac{y}{2}=1
अन्तःखण्ड
a=\frac{3}{2}, b=-2
Example:2(iii).3y+2=0
Solution: 3y +2=0 \\ \Rightarrow 0 . x+\frac{y}{\frac{3}{2}}=0
y-अक्ष पर अन्तःखण्ड=\frac{3}{2} , x-अक्ष पर कोई अन्तःखण्ड नहीं है।
Example:3.निम्नलिखित समीकरणों को लम्ब रूप में रूपान्तरित कीजिए।उनकी मूलबिन्दु से लाम्बिक दूरियाँ और लम्ब तथा धन x-अक्ष के बीच कोण ज्ञात कीजिएः
Example:3(i). x-\sqrt{3} y=8
Solution: x-\sqrt{3} y=8 \cdots(1)
समीकरण (1) को \sqrt{(1)^2+(-\sqrt{3})^2}=2 का भाग देने परः
\frac{x}{2}-\frac{\sqrt{3}}{2} y=4 \\ x \cos 300^{\circ}+y \sin 300^{\circ}=4
लम्ब=4,कोण=300°
Example:3(ii).y-2=0
Solution: y=2 … (1)
समीकरण (1) को \sqrt{0^2+(1)^2}=1 से भाग देने परः
\frac{0 \cdot x}{1}+\frac{y}{1}=2 \\ x \cos 90^{\circ}+y \sin 90^{\circ}=2
लम्ब=2,कोण=90°
Example:3(iii).x-y=4
Solution: x-y=4 … (1)
समीकरण (1) को \sqrt{(1)^2+(-1)^2}=\sqrt{2} से भाग देने परः
\frac{x}{\sqrt{2}}-\frac{y}{\sqrt{2}}=2 \sqrt{2} \\ x \cos 315^{\circ}+y \sin 315^{\circ}=2 \sqrt{2}
लम्ब=2 \sqrt{2}, कोण=315°
Example:4.बिन्दु (-1,1) की रेखा 12(x+6)=5(y-2) से दूरी ज्ञात कीजिए।
Solution: 12(x+6)=5(y-2) \\ \Rightarrow 12 x+72=5 y-10 \\ \Rightarrow 12 x-5 y+72+10=0 \\ \Rightarrow 12 x-5 y+82=0 \cdots(1)
(-1,1) से रेखा (1) की दूरी
d=\frac{\left|A x_1+B y_1+C\right|}{\sqrt{A^2+B^2}} \\=\frac{112(-1)+(-5)(1)+82 \mid}{\sqrt{(12)^2 +(-5)^2}} \\ =\frac{|-12-5+82|}{\sqrt{144+25}} \\ =\frac{1651}{\sqrt{169}} \\ =\frac{65}{13} \\ \Rightarrow d =5
Example:5.समान्तर रेखाओं के बीच की दूरी ज्ञात कीजिएः
Example:5(i).15x+8y-34=0 और 15x+8y+31=0
Solution:15x+8y-34=0 और 15x+8y+31=0 के बीच की दूरी
d=\frac{\left|C_1-C_2\right|}{\sqrt{A^2+B^2}} \\ d =\frac{1-34-311}{\sqrt{(15)^2+(8)^2}} \\ =\frac{1-651}{\sqrt{225+64}} \\ =\frac{65}{\sqrt{289}} \\ d =\frac{65}{17}
Example:5(ii).l(x+y)+p=0 और l(x+y)-r=0
Solution:lx+ly+p=0 और lx+ly-r=0 के बीच दूरी
d=\frac{\left|C_{1}-C_2\right|}{\sqrt{A^2+B^2} \mid} \\ d=\frac{|p+r|}{\sqrt{l^2+r^2}} \\ d=\frac{1}{\sqrt{2}}\left|\frac{p+r}{l}\right| \\ d=\frac{1}{\sqrt{2}}\left|\frac{p+r}{l}\right|
Example:6.x-अक्ष पर बिन्दुओं को ज्ञात कीजिए जिनकी रेखा \frac{x}{3}+\frac{y}{4}=1 से दूरियाँ 4 इकाई है।
Solution:x-अक्ष पर कोई बिन्दु \left(x_{1},0 \right) \\ \left(x_{1},0 \right) की रेखा \frac{x}{3}+\frac{y}{4}-1=0 से दूरी=4
\Rightarrow \frac{\left|\frac{x_1}{3}+\frac{0}{4}-1\right|}{\sqrt{\left(\frac{1}{3}\right)^2+\left(\frac{1}{4}\right)^2}}=4 \\ \Rightarrow \frac{\left|\frac{x_1}{3}-1\right|}{\sqrt{\frac{1}{9}+\frac{1}{16}}}=4 \\ \Rightarrow \frac{\left|\frac{x_1}{3}-1\right|}{\sqrt{\frac{16+9}{144}}}=4 \\ \Rightarrow \frac{x_1}{3}-1=\pm 4 \times \frac{5}{12} \\ \Rightarrow \frac{x_1}{3}-1=+\frac{5}{3} \\ \Rightarrow \frac{x_1}{3}=\frac{5}{3}+1 \\ \Rightarrow x_1=\frac{8}{3} \times 3 \\ \Rightarrow x_1=8 \\ \frac{x_{1}}{3}-1=-\frac{5}{3} \\ \Rightarrow \frac{x_{1}}{3}==-\frac{5}{3}+1 \\ \Rightarrow x_1=-\frac{2}{3} \times 3 \\ \Rightarrow x_1=-2
अतः x-अक्ष पर बिन्दु (-2,0) व (8,0) हैं।
Example:7.रेखा 3x-4y+2=0 के समान्तर और बिन्दु (-2,3) से जानेवाली रेखा का समीकरण ज्ञात कीजिए।
Solution:3x-4y+2=0 के समान्तर किसी रेखा का समीकरण 3 x-4 y+\lambda=0
यह (-2,3) से गुजरती हैं अतः 3 x-2-4 \times 3+\lambda=0 \\ \Rightarrow-6-12+\lambda=0 \Rightarrow \lambda=18
अतः रेखा का समीकरणः3x-4y+18=0
Example:8.रेखा x-7y+5=0 पर लम्ब और x-अन्तःखण्ड 3 वाली रेखा का समीकरण ज्ञात कीजिए।
Solution: x-7 y+5=0 \\ y=\frac{1}{7} x+\frac{5}{7} \cdots(1)
(1) पर लम्ब रेखा की ढाल=m_2 \\ m_1 m_2 =-1 \\ \Rightarrow \frac{1}{7} m_2 =-1 \Rightarrow m_2=-7
m ढाल वाली रेखा x-अन्तःखण्ड d बनाती है तो रेखा का समीकरणः
y=m(x-d) \\ \Rightarrow y=-7(x-3) \\ \Rightarrow y+7 x=21
Example:9.रेखाओं \sqrt{3} x+y=1 और x+\sqrt{3} y=1 के बीच का कोण ज्ञात कीजिए।
Solution: \sqrt{3} x+y=1 \cdots(1)\\ x+\sqrt{3} y=1 \cdots(2)
रेखा (1) की ढाल m_1=-\sqrt{3}
रेखा (2) की ढाल m_2=-\frac{1}{\sqrt{3}}
दोनों रेखाओं के बीच न्यूनकोण
\tan \theta =\left|\frac{m_1-m_1}{1+m_1 m_2}\right| \\ =\left|\frac{-\frac{1}{\sqrt{3}}+\sqrt{3}}{1+\left(-\frac{1}{\sqrt{3}}\right)(-\sqrt{3})}\right| \\ =\left|\frac{\frac{-1+3}{\sqrt{3}}}{1+1}\right| \\ =\frac{1}{\sqrt{3}} \\ \Rightarrow \tan \theta =\tan 30^{\circ}
अतः दोनों रेखाओं के बीच कोण या तो 30° या 180°-30°=150° है।
Example:10.बिन्दुओं (h,3) और (4,1) से जानेवाली रेखा,रेखा 7x-9y-19=0 को समकोण पर प्रतिच्छेद करती है।h का मान ज्ञात कीजिए।
Solution:(h,3) और (4,1) से जानेवाली रेखा की प्रवणता m_1=\frac{y_2-y_1}{x_2-x_1} \\ \Rightarrow m_1=\frac{1-3}{4-h} \\ \Rightarrow m_1=\frac{-2}{4-h}
रेखा 7x-9y-19=0 की प्रवणता
m_2=-\frac{x \text{का गुणांक}}{y \text{का गुणांक}} =\frac{-7}{-9} \\ \Rightarrow m_2=\frac{7}{9}
लम्बवत होने का प्रतिबन्ध m_1 m_2=-1 \\ \Rightarrow\left(\frac{-2}{4-h}\right)\left (\frac{7}{9}\right )=-1 \\ \Rightarrow 14 =36-9 h \\ \Rightarrow 9 h =36-14 \Rightarrow h=\frac{22}{9}
Example:11.सिद्ध कीजिए कि बिन्दु \left( x_{1},y_{1} \right) से जानेवाली और रेखा Ax+By+C=0 के समान्तर रेखा का समीकरण A\left(x-x_1\right)+B\left(y-y_1\right)=0 है।
Solution:Ax+By+C=0 के समान्तर रेखा का समीकरणः A x+B y+\lambda=0 \cdots(1)
यह \left( x_{1},y_{1} \right) से गुजरती है अतः
A x_1+B y_1+\lambda=0 \\ \Rightarrow \lambda=-A x_1-B y_1
अतः समान्तर रेखा का समीकरण (1) सेः A x+B y-A x_1-B y_1=0 \\ \left(x-x_1\right)+B\left(y-y_1\right)=0
Example:12.बिन्दु (2,3) से जानेवाली दो रेखाएँ परस्पर 60° के कोण पर प्रतिच्छेद करती हैं।यदि एक रेखा की ढाल 2 है तो दूसरी रेखा का समीकरण ज्ञात कीजिए।
Solution: m_1=2
दो रेखाओं के बीच कोण \tan \theta=\left|\frac{m_2-m_1}{1+ m_1 m_{2}}\right| \\ \Rightarrow \tan 60^{\circ}=\left|\frac{m_2-2}{1+2 m_2}\right| \\ \sqrt{3}=\left|\frac{m_2-2}{1+2 m_2}\right| \\ \Rightarrow \pm \sqrt{3}=\frac{m_2-2}{1+2 m_2} \\ \Rightarrow\left(1+2 m_2\right)(\pm \sqrt{3})=m_2-2
धनात्मक चिन्ह लेने परः \sqrt{3}+2 \sqrt{3} m_2=m_2-2 \\ 2 \sqrt{3} m_2-m_2=-2-\sqrt{3} \\ \Rightarrow m_2(2 \sqrt{3}-1)=-(\sqrt{3}+2) \\ \Rightarrow m_2=-\frac{(\sqrt{3}+2)}{2 \sqrt{3}-1}
ऋणात्मक चिन्ह लेने परः -\sqrt{3}=\frac{m_2-2}{1+2 m_2} \\ \Rightarrow-\sqrt{3}-2 \sqrt{3} m_2=m_2-2 \\ \Rightarrow 2 \sqrt{3} m_2+m_2=2-\sqrt{3} \\ \Rightarrow m_2(2 \sqrt{3}+1)=2-\sqrt{3} \\ \Rightarrow m_2=\frac{2-\sqrt{3}}{2 \sqrt{3}+1}
रेखा का समीकरण जो (2,3) से गुजरती हैः
y-y_1=m\left(x-x_1\right) \\ \Rightarrow y-3=-\frac{(\sqrt{3}+2)}{2 \sqrt{3}-1}(x-2) \\ \Rightarrow (\sqrt{3}+2) x+(2 \sqrt{3}-1) y=8 \sqrt{3}+1
तथा y-3=\left(\frac{2-\sqrt{3}}{2 \sqrt{3}+1}\right)(x-2) \\ \Rightarrow(\sqrt{3}-2) x+(1+2 \sqrt{3}) y=-1+8 \sqrt{3}
Example:13.बिन्दुओं (3,4) और (-1,2) को मिलाने वाली रेखाखण्ड के लम्ब समद्विभाजक रेखा का समीकरण ज्ञात कीजिए।
Solution:(3, 4) व (-1,2) के मध्य बिन्दु के निर्देशांक \left(x=\frac{x_1+x_2}{2}, y=\frac{y_1+y_2}{2}\right) \\ \left(\frac{3-1}{2}, \frac{4+2}{2}\right)=(1,3)
(3,4) व (-1,2) से गुजरने वाली रेखा की प्रवणता m_1=\frac{y_2-y_1}{x_2-x_1}=\frac{2-4}{-1-3}=\frac{-2}{-4} \\ m_1=\frac{1}{2}
लम्बवत रेखाओं का प्रतिबन्ध m_{1} m_{2}=-1 \\ \left(\frac{1}{2}\right) m_2=-1 \\ \Rightarrow m_2=-2
(1,3) से गुजरने वाली तथा – 2 प्रवणता वाली रेखा की समीकरण
y-y_1=m\left(x-x_1\right) \\ \Rightarrow y-3=-2(x-1) \\ \Rightarrow y-3=-2 x+2 \\ \Rightarrow 2 x+y=5
Example:14.बिन्दु (-1,3) से रेखा 3x-4y-16=0 पर डाले गए लम्बपाद के निर्देशांक ज्ञात कीजिए।
Solution:रेखा 3x-4y-16=0 की प्रवणता
m_{1}=-\frac{x \text{का गुणांक} }{y \text{ का गुणांक}}=-\frac{3}{(-4)}=\frac{3}{4}
माना लम्बपाद के निर्देशांक \left(x_{1},y_{1} \right)
(-1,3) व \left(x_{1},y_{1} \right) से गुजरने वाली रेखा की प्रवणता
m_2=\frac{y_1-3}{x_1+1} \\ m_1 m_2=-1 \\ \Rightarrow \frac{y_1-3}{x_1+1} \times \frac{3}{4}=-1 \\ \Rightarrow 3 y_1-9=-4 x_1-4 \\ \Rightarrow 4 x_1+3 y_1=5 \cdots(1)
लम्बपाद \left(x_{1},y_{1} \right) रेखा 3x-4y-16=0 पर है अतः
3 x_1-4 y_1=16 \cdots{2}
(1) व (2) को हल करने परः
x_1=\frac{68}{25}, y_1=-\frac{49}{25} \\ \Rightarrow \left(\frac{68}{25},-\frac{49}{25}\right)
Example:15.मूलबिन्दु से रेखा y=mx+c पर डाला गया लम्ब रेखा से बिन्दु(-1,2)पर मिलता है।m और c के मान ज्ञात कीजिए।
Solution:(0,0) से रेखा y-mx-c=0 पर लम्ब
\frac{|(0)-m(0)-c|}{\sqrt{1+m^2}}=\sqrt{(-1-0)^2+(2-0)^2} \\ \Rightarrow \frac{c}{\sqrt{1+m^2}}= \sqrt{5} \\ \Rightarrow c^2=5\left(1+m^2\right) \cdots(1)
(-1,2) रेखा y=mx+c पर स्थित है अतः
2=-m+c \Rightarrow m=c-2 \cdots(2)
(1) व (2) सेः
c^2=5\left[1+(c-2)^2\right] \\ \Rightarrow c^2=5\left[1+c^2-4 c+4\right] \\ \Rightarrow c^2=5+5 c^2-20 c+20 \\ \Rightarrow 4 c^2-20 c+25-0 \\ \Rightarrow 4 c^2-10 c-10 c+25=0 \\ \Rightarrow \left(2 c-5\right)^2=0 \Rightarrow c=\frac{5}{2}
(2) में रखने परः m=\frac{5}{2}-2=\frac{1}{2} \\ m=\frac{1}{2} ; c=\frac{5}{2}
Example:16.यदि p और q क्रमशः मूलबिन्दु से रेखाओं x \cos \theta-y \sin \theta =k \cos 2 \theta और x \sec \theta+y \operatorname{cosec} \theta=k पर लम्ब की लम्बाईयाँ हैं तो सिद्ध कीजिए कि p^2+4 q^2=k^2
Solution:मूलबिन्दु से रेखाओं x \cos \theta-y \sin \theta-k \cos 2 \theta=0 तथा x \sec \theta+y \operatorname{cosec} \theta=k=0 पर लम्ब की लम्बाईयाँ
\frac{\mid 0( \cos \theta)-0(\sin \theta)-k \cos 2 \theta \mid}{\sqrt{\cos ^2 \theta+(-\sin \theta)^2}} = p \\ \Rightarrow \frac{k^2 \cos ^2 2 \theta}{1}=p^2 \\ \Rightarrow p^2=k^2 \cos ^2 2 \theta \\ \frac{|0 (\sec \theta)+0 (\operatorname{cosec} \theta)-k\mid}{\sqrt{\sec ^2 \theta+ \operatorname{cosec}^{2} \theta}}=q \\ \Rightarrow \frac{k^2}{\sqrt{\sec ^2 \theta+ \operatorname{cosec}^2 \theta}}=q \\ \Rightarrow \frac{k^2}{\frac{1}{\cos ^2 \theta}+\frac{1}{\sin ^2 \theta}}=q^2 \\ \Rightarrow q^2=k^2 \sin ^2 \theta \cos ^2 \theta \\ \Rightarrow p^2+4 q^2=k^2 \cos ^2 2 \theta+4 k^2 \sin ^2 \theta \cos ^2 \theta \\ =k^2\left(\cos ^2 2 \theta+\sin ^2 2 \theta\right) \\ \Rightarrow p^2+4 q^2=k^2
Example:17.शीर्षों A(2,3),B(4,-1) और C(1,2) वाले त्रिभुज ABC के शीर्ष A से उसकी सम्मुख भुजा पर लम्ब डाला गया है।लम्ब की लम्बाई तथा समीकरण ज्ञात कीजिए।
Solution:भुजा BC का समीकरण
y-y_1 =\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right) \\ y+1 =\left(\frac{2+1}{1-4}\right)(x-4) \\ \Rightarrow y+1 =\frac{3}{-3}(x-4)\\ \Rightarrow x+y-24=0
A(2,3) से x+y-4=0 पर लम्ब की लम्बाई
\frac{|2+3-4|}{\sqrt{1^2+1^2}}=\frac{1}{\sqrt{2}}
x+y-4=0 की प्रवणता m_{1}=-\frac{ x \text{ का गुणांक }}{ y \text{ का गुणांक } }=-1
A(2,3) से शीर्ष लम्ब की प्रवणता=m_{2} \\ m_1 m_2=-1 \Rightarrow(-1) m_2=-1 \Rightarrow m_2=1
अतः शीर्ष लम्ब की समीकरण y-y_1=m\left(x-x_{1}\right) \\ y-3=1(x-2) \\ \Rightarrow y-x=1
Example:18.यदि p मूलबिन्दु से उस रेखा पर डाले गए लम्ब की लम्बाई हो जिस पर अक्षों पर कटे अन्तःखण्ड a और b हों तो दिखाइए कि \frac{1}{b^2}=\frac{1}{a^2}+\frac{1}{b^2}
Solution:रेखा का समीकरण \frac{x}{a}+\frac{y}{b}=1
मूलबिन्दु से लम्ब की लम्बाई \frac{\left|\frac{0}{a}+\frac{0}{b}-1\right|}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}}}=p \\ \Rightarrow \frac{1}{b^2}=\frac{1}{a^2}+\frac{1}{b^2}
उपर्युक्त उदाहरणों के द्वारा रेखा का व्यापक समीकरण कक्षा 11 (General Equation of Line Class 11),गणित में रेखा का व्यापक समीकरण (General Equation of Line Class 11 in Mathematics) को समझ सकते हैं।
3.रेखा का व्यापक समीकरण कक्षा 11 पर आधारित सवाल (Questions Based on General Equation of Line Class 11):
(1.)निम्नलिखित सरल रेखाओं के मध्य कोण ज्ञात कीजिएः y=(2-\sqrt{3}) x+5 तथा y=(2+\sqrt{3}) x-7
(2.)सिद्ध कीजिए कि बिन्दु \left(a \cos^3 \theta, a \sin^3 \theta\right) से गुजरने वाली तथा सरल रेखा x \sec \theta +y \operatorname{cosec} \theta=a पर लम्ब सरल रेखा का समीकरण x \cos \theta-y \sin \theta= a \cos 2 \theta है।
उत्तर (Answer):(1.) 120° या 60°
उपर्युक्त सवालों को हल करने पर रेखा का व्यापक समीकरण कक्षा 11 (General Equation of Line Class 11),गणित में रेखा का व्यापक समीकरण (General Equation of Line Class 11 in Mathematics) को ठीक से समझ सकते हैं।
Also Read This Article:-Geometric and Arithmetic Progression
4.रेखा का व्यापक समीकरण कक्षा 11 (Frequently Asked Questions Related to General Equation of Line Class 11),गणित में रेखा का व्यापक समीकरण (General Equation of Line Class 11 in Mathematics) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्नः
प्रश्नः1.दो सरल रेखाओं के समान्तर होने का आवश्यक प्रतिबन्ध लिखो जबकि रेखाएँ ढाल रूप में हो। (Write the Necessary Condition for Two Lines to be Parallel When the Lines are in Slope Form):
उत्तरःमाना कि ढाल के रूप में रेखाओं के समीकरण y=m_1 x+c_1 तथा y=m_2 x+c_2 है।
इन दोनों रेखाओं के मध्य कोण \theta हो तो
\tan \theta=\pm \frac{m_1-m_2}{1+m_1 m_2}
दोनों रेखाएँ समान्तर हैं अतः \theta=0 अर्थात् \tan \theta=\tan 0 \\ \tan 0=\frac{m_1-m_2}{1+m_1 m_2} \Rightarrow m_1=m_2
इस प्रकार दो रेखाएँ समान्तर हैं तो उनकी प्रवणताएँ समान होंगी।
प्रश्न:2.दो सरल रेखाओं के समान्तर होने का आवश्यक प्रतिबन्ध लिखो जब रेखाएँ व्यापक रूप में हों। (Write the Necessary Condition for Two Lines to be Parallel When the Lines are in General Form):
उत्तरःमाना कि व्यापक रूप में दो रेखाओं के समीकरण निम्न हैंः
a_1 x+b_1 y+c_1=0 \\ a_2 x+b_2 y+c_2=0
यदि इन रेखाओं के मध्य कोण \theta हो तो सूत्रानुसारः
\theta=\pm \frac{a_1 b_1-a_2 b_2}{a_1 a_2+b_1 b_2} \cdots(3)
रेखाएँ समान्तर हैं अतः \theta शून्य होगा अर्थात्
\tan \theta=\tan 0 \\ \tan 0= \pm \frac{a_2 b_1-a_2 b_2}{a_1 a_2+b_1 b_2} \\ \Rightarrow \theta=a_2 b_1-a_1 b_2 \\ \Rightarrow \frac{a_1}{a_2}=\frac{b_1}{b_2}
प्रश्न:3.दो रेखाओं के लम्ब होने का आवश्यक प्रतिबन्ध लिखिए जबकि रेखाएँ ढाल रूप में हों। (Write Necessary Condition for Two Lines to be Mutually Perpendicular When the Lines are in Slope Form):
उत्तरः y=m_1 x+c_{1} \cdots(1) \\ y=m_2 x+c_2=0
माना कि दी हुई सरल रेखाओं के मध्य कोण हो तो
\tan \theta=\pm \frac{m_2-m_1}{1+m_{1}m_{2}}
यदि ये रेखाएँ परस्पर लम्बवत हों तो \theta=90 अर्थात्
\tan \theta =\tan 9 0^{\circ}=\infty
अतः 1+m_1 m_2=0 \Rightarrow m_1 m_2=-1
अतः दो परस्पर लम्बवत रेखाओं की प्रवणताओं का गुणनफल – 1 होता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा रेखा का व्यापक समीकरण कक्षा 11 (General Equation of Line Class 11),गणित में रेखा का व्यापक समीकरण (General Equation of Line Class 11 in Mathematics) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
General Equation of Line Class 11
रेखा का व्यापक समीकरण कक्षा 11
(General Equation of Line Class 11)
General Equation of Line Class 11
रेखा का व्यापक समीकरण कक्षा 11 (General Equation of Line Class 11) Ax+By+C=0
का लेखाचित्र सदैव एक सरल रेखा होता है।इसलिए जब A और B एक साथ शून्य नहीं हैं
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.