Orthogonality condition of two spheres
1.दो गोलों की लाम्बिकता का प्रतिबन्ध का परिचय (Introduction to Orthogonality condition of two spheres)-
दो गोलों की लाम्बिकता का प्रतिबन्ध (Orthogonality condition of two spheres) से तात्पर्य यह है कि जब दो गोले एक दूसरे को प्रतिच्छेद करते हैं तो प्रतिच्छेद बिन्दु से गुजरने वाली त्रिज्याओं के बीच का कोण समकोण होता है।इस प्रकार दो गोलों का प्रतिच्छेदन कोण एक समकोण (right angle) हो तो ऐसे गोलों को लाम्बिक गोले कहते हैं।इस आर्टिकल में दो गोलों की लाम्बिकता का प्रतिबन्ध (Orthogonality condition of two spheres) ज्ञात करेंगे तथा दो गोलों की लाम्बिकता का प्रतिबन्ध (Orthogonality condition of two spheres) को कुछ सवालों के हल द्वारा समझेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Diameter form of equation of sphere
2.दो गोलों की लाम्बिकता का प्रतिबन्ध (Orthogonality condition of two spheres)-
मान लो दो गोलों के समीकरण हैं
{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2{ u }_{ 1 }x+2{ v }_{ 1 }y+2{ w }_{ 1 }z+{ d }_{ 1 }=0.....(1)
तथा { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2{ u }_{ 2 }x+2{ v }_{ 2 }y+2{ w }_{ 2 }z+{ d }_{ 2 }=0.....(2)
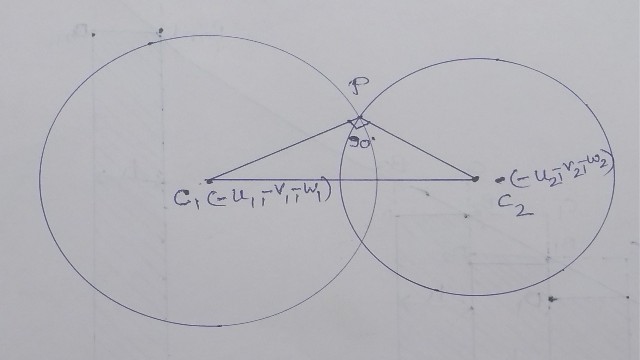
मान लो { c }_{ 1 } तथा { c }_{ 2 } क्रमशः गोले (1) व (2) के केन्द्र हैं,तो इनके निर्देशांक \left( { -u }_{ 1 },-{ v }_{ 1 },-{ w }_{ 1 } \right) तथा \left( { -u }_{ 2 },-{ v }_{ 2 },-{ w }_{ 2 } \right) होंगे।
इन गोलों की त्रिज्याएं-
c_{ 1 }p=\sqrt { { { u }_{ 1 } }^{ 2 }+{ v_{ 1 } }^{ 2 }+{ w_{ 1 } }^{ 2 }-{ d }_{ 1 } } \\ c_{ 2 }p=\sqrt { { { u }_{ 2 } }^{ 2 }+{ v_{ 2 } }^{ 2 }+{ w_{ 2 } }^{ 2 }-{ d }_{ 2 } }
चूंकि दोनों गोले लाम्बिक हैं, अतः इनका प्रतिच्छेदन कोण एक समकोण होगा अर्थात् \angle { c }_{ 1 }p{ c }_{ 2 }={ 90 }^{ \circ }
पुनः समकोण \triangle { c }_{ 1 }p{ c }_{ 2 } में
{ { c }_{ 1 }{ c }_{ 2 } }^{ 2 }={ c_{ 1 }p }^{ 2 }+{ c_{ 2 }p }^{ 2 }\\ { \left( { u }_{ 1 }{ -u }_{ 2 } \right) }^{ 2 }+{ \left( { v }_{ 1 }-v_{ 2 } \right) }^{ 2 }+{ \left( { w }_{ 1 }{ -w }_{ 2 } \right) }^{ 2 }=\left( { { { u }_{ 1 } }^{ 2 }+{ v_{ 1 } }^{ 2 }+{ w_{ 1 } }^{ 2 }-{ d }_{ 1 } } \right) +\left( { { u }_{ 2 } }^{ 2 }+{ v_{ 2 } }^{ 2 }+{ w_{ 2 } }^{ 2 }-{ d }_{ 2 } \right) \\ \Rightarrow 2{ u }_{ 1 }{ u }_{ 2 }+2{ v }_{ 1 }v_{ 2 }+{ 2w }_{ 1 }{ w }_{ 2 }={ d }_{ 1 }+{ d }_{ 2 }
जो कि दो गोलों की लाम्बिकता का प्रतिबन्ध (Orthogonality condition of two spheres) है।
3.दो गोलों की लाम्बिकता का प्रतिबन्ध (Orthogonality condition of two spheres) पर आधारित सवाल-
Question-1.निम्न गोलों को लाम्बिक रूप से काटने वाले गोले का समीकरण ज्ञात करो:
(Find the equations of the sphere which cuts the following spheres orthogonally:)
{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }={ a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 }\\ { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2ax={ a }^{ 2 }\\ { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2by={ b }^{ 2 }\\ { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2cz={ c }^{ 2 }
Solution-माना दिए हुए गोलों को लाम्बिक रूप काटने वाले गोले का समीकरण-
{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2ux+2vy+2wz+d=0.......(1)\\ { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }={ a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 }.....(2)\\ { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2ax={ a }^{ 2 }.....(3)\\ { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2by={ b }^{ 2 }......(4)\\ { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2cz={ c }^{ 2 }.......(5)
गोला (1) गोलों (2),(3),(4),(5) को लाम्बिक रूप से काटता है। अतःदो गोलों की लाम्बिकता का प्रतिबन्ध (Orthogonality condition of two spheres) से-
2{ u }_{ 1 }{ u }_{ 2 }+2{ v }_{ 1 }v_{ 2 }+{ 2w }_{ 1 }{ w }_{ 2 }={ d }_{ 1 }+{ d }_{ 2 }\\ 2u\left( 0 \right) +2v\left( 0 \right) +2w\left( 0 \right) =d-{ a }^{ 2 }-{ b }^{ 2 }-{ c }^{ 2 }\\ \Rightarrow d={ a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 }\\ 2u\left( a \right) +2v\left( 0 \right) +2w\left( 0 \right) ={ a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 }-{ a }^{ 2 }\\ \Rightarrow 2ua={ b }^{ 2 }+{ c }^{ 2 }\\ \Rightarrow u=\frac { { b }^{ 2 }+{ c }^{ 2 } }{ 2a } \\ 2u\left( 0 \right) +2v\left( b \right) +2w\left( 0 \right) ={ a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 }-{ b }^{ 2 }\\ \Rightarrow 2vb={ a }^{ 2 }+{ c }^{ 2 }\\ \Rightarrow v=\frac { { a }^{ 2 }+{ c }^{ 2 } }{ 2b } \\ 2u\left( 0 \right) +2v\left( 0 \right) +2w\left( c \right) ={ a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 }-{ c }^{ 2 }\\ \Rightarrow 2wc={ a }^{ 2 }+{ b }^{ 2 }\\ \Rightarrow w=\frac { { a }^{ 2 }+{ b }^{ 2 } }{ 2c }
u,v,w व d के मान समीकरण (1) में रखने पर-
{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+\left( \frac { { b }^{ 2 }+{ c }^{ 2 } }{ 2a } \right) x+\left( \frac { { a }^{ 2 }+{ c }^{ 2 } }{ 2b } \right) y+\left( \frac { { a }^{ 2 }+{ b }^{ 2 } }{ 2c } \right) z+{ a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 }=0
Question-2दो बिन्दुओं (0,3,0) और (-2,-1,-4) से गुजरने वाले उस गोले का समीकरण ज्ञात करो जो कि { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+x-3z-2=0 तथा 2\left( { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 } \right) +x+3y+4=0
गोलों को लाम्बिक रूप से काटता है।
(Find the equation of the sphere that passes through the two points (0,3,0) and (-2,-1,-4) and cuts orthogonally the two spheres
{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+x-3z-2=0
and 2\left( { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 } \right) +x+3y+4=0
Solution-माना गोले का समीकरण है-
{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2ux+2vy+2wz+d=0.....(1)
उपर्युक्त गोला बिन्दुओं (0,3,0) तथा (-2,-1,-4) से गुजरता है
अतः 9+6v+d=0
\Rightarrow 6v+d=-9...(2)
{ \left( -2 \right) }^{ 2 }+{ \left( -1 \right) }^{ 2 }+{ \left( -4 \right) }^{ 2 }+2u\left( -2 \right) +2v\left( -1 \right) +3w\left( -4 \right) +d=0 \\\Rightarrow 4+1+16-4u-2v-8w+d=0\\ -4u-2v-8w+d=-21....(3)\\ \Rightarrow 6v+d=-9....(2)\\ -\quad \quad \quad -\quad \quad \quad +\\ ---------------
घटाने पर
\Rightarrow -4u-8w=-12\\ \Rightarrow 4+2v+2w=3....(4)\\{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+x-3z-2=0......(5)\\ 2\left( { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 } \right) +x+3y+4=0\\ \Rightarrow { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+\frac { x }{ 2 } +\frac { 3y }{ 2 } +2=0......(6)
गोला (1),गोले(5) व (6) को लाम्बिक रूप से काटता है।दो गोलों की लाम्बिकता का प्रतिबन्ध (Orthogonality condition of two spheres) से-
2{ u }_{ 1 }{ u }_{ 2 }+2{ v }_{ 1 }v_{ 2 }+{ 2w }_{ 1 }{ w }_{ 2 }={ d }_{ 1 }+{ d }_{ 2 }\\ 2u\left( \frac { 1 }{ 2 } \right) +2v\left( 0 \right) +2w\left( -\frac { 3 }{ 2 } \right) =d-2\\ \Rightarrow u-3w=d-2\\ \Rightarrow u-3w-d=-2.....(7)\\ 2u\left( \frac { 1 }{ 4 } \right) +2v\left( \frac { 3 }{ 4 } \right) +2w\left( 0 \right) =d+2\\ \Rightarrow \frac { u }{ 2 } +\frac { 3v }{ 2 } =d+2\\ \Rightarrow \frac { u }{ 2 } +\frac { 3v }{ 2 } -d=2.....(8)\\ 6v+d=-9......(2)
जोड़ने पर
\frac { u }{ 2 } +\frac { 15v }{ 2 } =-7\\ u+15v=-14.....(9)
समीकरण (2) व (7) से-
u-3w-d=-2 ………..(7)
6v+d=-9 ………..(2)
————————————-
जोड़ने पर
u+6v-3w=-11 ……….(10)
समीकरण (4) को 3 से तथा समीकरण (10) को 2 से गुणा करके जोड़ने पर-
3u+6v+6w=9 …….(11)
2u+12v-6w=-22 …….(12)
—————————–
जोड़ने पर
5u+18v=-13 …………..(13)
समीकरण (9) को 5 से गुणा करने पर-
5u+75v=-70 …………….(14)
5u+18v=-13 …………….(13)
– – +
—————————————–
घटाने पर
57v=-57
v=-1
v का मान समीकरण (9) में रखने पर-
u+15(-1)=-14
u=15-14
u=1
v का मान समीकरण (2) में रखने पर-
6(-1)+d=-9
d=6-9
d=-3
u तथा d का मान समीकरण (7) में रखने पर-
1-3w+3=-2
-3w=-6
w=2
u,v,w व d का मान समीकरण (1) में रखने पर-
{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2x-2y+4z-3=0
Question-3.वृत्त { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2x+y-3z-1=0
,x+2y+5z+7=0 से गुजरने वाले उस गोले { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }-7x-3y+5z-6=0 का समीकरण ज्ञात कीजिए जो गोले को लाम्बिक रूप से काटता है।
(Find the equation of a sphere that passes through the circle { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2x+y-3z-1=0 ,-x+2y+5z+7=0 and cuts the sphere { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }-7x-3y+5z-6=0
orthogonally.)
Solution-माना { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2x+y-3z-1=0 वृत्त -x+2y+5z+7=0 से गुजरने वाले गोले का समीकरण-
\left( { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2x+y-3z-1 \right) +\lambda \left( -x+2y+5z+7 \right) =0\\ \Rightarrow { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+\left( 2-\lambda \right) x+\left( 1+2\lambda \right) y+\left( -3+5\lambda \right) z-1+7\lambda =0......(1)\\ { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }-7x-3y+5z-6=0.......(2)
गोला (1) गोले (2) को लाम्बिक रूप काटता है। अतःदो गोलों की लाम्बिकता का प्रतिबन्ध (Orthogonality condition of two spheres) से-
2{ u }_{ 1 }{ u }_{ 2 }+2{ v }_{ 1 }v_{ 2 }+{ 2w }_{ 1 }{ w }_{ 2 }={ d }_{ 1 }+{ d }_{ 2 }\\ 2\frac { \left( 2-\lambda \right) }{ 2 } \left( -\frac { 7 }{ 2 } \right) +2\left( \frac { 1+2\lambda }{ 2 } \right) \left( -\frac { 3 }{ 2 } \right) +2\left( \frac { -3+5\lambda }{ 2 } \right) \left( \frac { 5 }{ 2 } \right) =-1+7\lambda -6\\ \Rightarrow -14+7\lambda -3-6\lambda -15+25\lambda =-2+14\lambda -12\\ \Rightarrow -12\lambda =-18\\ \Rightarrow \lambda =\frac { 3 }{ 2 }
\lambda का मान समीकरण (1) में रखने पर-
2\left( { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 } \right) +x+8y+9z+19=0
उपर्युक्त सवालों के हल द्वारा दो गोलों की लाम्बिकता का प्रतिबन्ध (Orthogonality condition of two spheres) को समझा जा सकता है।
Also Read This Article:-Equation of tangent-plane of sphere
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |