Diameter form of equation of sphere
1.व्यास रूप में गोले का समीकरण का परिचय (Introduction to Diameter form of equation of sphere):
व्यास रूप में गोले का समीकरण (Diameter form of equation of sphere) ज्ञात करने का तात्पर्य यह है कि यदि किसी गोले के व्यास के सिरों के निर्देशांक दिए हुए हों तो गोले का समीकरण ज्ञात करना है।यह वस्तुत: उसी प्रकार है जैसे किसी वृत्त के व्यास के सिरे दिए हुए हों तो वृत्त का समीकरण ज्ञात करना। दोनों में इतना ही फर्क है कि गोला त्रिविमीय आकृति है जबकि वृत्त द्विविमीय आकृति है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Length of plane curves (Rectification)
2.व्यास रूप में गोले का समीकरण (Diameter form of equation of sphere)-
एक ऐसे गोले का समीकरण ज्ञात करना जिसके व्यास के सिरे \left( { x }_{ 1 },{ y }_{ 1 },{ z }_{ 1 } \right) \quad और\quad \left( { x }_{ 2 },{ y }_{ 2 },{ z }_{ 2 } \right) हैं।
(To find the equation of the sphere, the extremities of whose diameter being and .
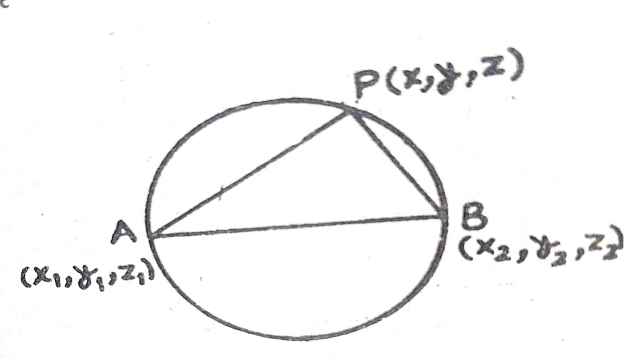
मान लो दिए गए बिन्दु A \left( { x }_{ 1 },{ y }_{ 1 },{ z }_{ 1 } \right)तथा B\left( { x }_{ 2 },{ y }_{ 2 },{ z }_{ 2 } \right) व्यास के सिरे हैं तथा P(x,y,z) गोले पर स्थित कोई एक-बिन्दु है,तब
रेखा PA के दिक्-अनुपात x-{ x }_{ 1 } , y-{ y }_{ 1 } z-{ z }_{ 1 } तथा रेखा PB के दिक्-अनुपात x-{ x }_{ 2 } , y-{ y }_{ 2 } z-{ z }_{ 2 } होंगे।
चूंकि तीन बिन्दुओंP,A,B से गुजरने वाले समतल से
गोले का प्रतिच्छेदन वृहत वृत्त (great circle) होगा जिसका व्यास AB है। अतः P एक अर्धवृत्त पर स्थित होगा तथा\angle APB={ 90 }^{ \circ } होगा अर्थात् PA तथा PB परस्पर लम्बवत् होंगे।
\left( x-{ x }_{ 1 } \right) \left( x-{ x }_{ 2 } \right) +\left( y-{ y }_{ 1 } \right) \left( y-{ y }_{ 2 } \right) +\left( z-{ z }_{ 1 } \right) \left( z-{ z }_{ 2 } \right) =0
जो कि P की प्रत्येक स्थिति के लिए सत्य है। अतः यह गोले का अभीष्ट समीकरण है।
Question-1.उस गोले का समीकरण ज्ञात कीजिए जिसके एक व्यास के सिरे (2,-1,4) और (-2,2,-2) है।उस वृत्त का क्षेत्रफल भी ज्ञात कीजिए जिसमें समतल 2x+y-z=3 इस गोले को काटती है।
(Find the equation of the sphere described on the line joining the points (2,-1,4) and (-2,2,-2) as diameter.Also find the area of the circle in which this sphere is cut by the plane 2x+y-z=3.
Solution-व्यास रूप में गोले का समीकरण
\left( x-{ x }_{ 1 } \right) \left( x-{ x }_{ 2 } \right) +\left( y-{ y }_{ 1 } \right) \left( y-{ y }_{ 2 } \right) +\left( z-{ z }_{ 1 } \right) \left( z-{ z }_{ 2 } \right) =0......(1)\\ \left( { x }_{ 1 },{ y }_{ 1 },{ z }_{ 1 } \right) =(2,-1,4)\quad तथा\quad \left( { x }_{ 2 },{ y }_{ 2 },{ z }_{ 2 } \right) =(-2,2,-2)
मान रखने पर-
\left( x-2 \right) \left( x+2 \right) +\left( y+1 \right) \left( y-2 \right) +\left( z-4 \right) \left( z+2 \right) =0\\ { x }^{ 2 }-4+{ y }^{ 2 }-2y+y-2+{ z }^{ 2 }+2z-4z-8=0\\ { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }-y-2z-4z-14=0
गोले का केन्द्र\left( -u,-v,-w \right) =\left( 0,\frac { 1 }{ 2 } ,1 \right) \quad ,\quad c=-14
गोले की त्रिज्याr=\sqrt { u^{ 2 }+{ v }^{ 2 }+{ w }^{ 2 }-c } \\ r=\sqrt { { \left( 0 \right) }^{ 2 }+{ \left( -\frac { 1 }{ 2 } \right) }^{ 2 }+{ \left( -1 \right) }^{ 2 }+14 } \\ r=\sqrt { \frac { 1 }{ 4 } +1+14 } \\ r=\sqrt { \frac { 61 }{ 4 } }
समतल 2x+y-z=3 पर गोले के केन्द्र\left( 0,\frac { 1 }{ 2 } ,1 \right) से लम्ब की लम्बाई
p=\left| \frac { 2\left( 0 \right) +\frac { 1 }{ 2 } -1-3 }{ \sqrt { { \left( 2 \right) }^{ 2 }+{ \left( 1 \right) }^{ 2 }+{ \left( 1 \right) }^{ 2 } } } \right| \\ p=\frac { \frac { 7 }{ 2 } }{ \sqrt { 6 } } \\ p=\frac { 7 }{ 2\sqrt { 6 } }
वृत्त की त्रिज्या R=\sqrt { { r }^{ 2 }-{ p }^{ 2 } } \\ R=\sqrt { \frac { 61 }{ 4 } -{ \left( \frac { 7 }{ 2\sqrt { 6 } } \right) }^{ 2 } } \\ R=\sqrt { \frac { 61 }{ 4 } -\frac { 49 }{ 24 } } \\ R=\sqrt { \frac { 366-49 }{ 24 } } \\ R=\sqrt { \frac { 317 }{ 24 } }
वृत्त का क्षेत्रफल=\pi { R }^{ 2 }\\ =\pi \times \frac { 317 }{ 24 } =\frac { 317\pi }{ 24 }
Question-2.उस गोले का समीकरण ज्ञात कीजिए जिसका वृहत् वृत्त { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+7y-2z+2=0,2x+3y+4z=8 है।
(Find the equation of the sphere for which the circle { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+7y-2z+2=0,2x+3y+4z=8 is a great circle.)
Solution-वृहत वृत्त का समीकरण-
{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+7y-2z+2=0,2x+3y+4z=8
गोले का समीकरण-{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+7y-2z+2+\lambda \left( 2x+3y+4z-8 \right) =0\\{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2\lambda x+\left( 7+3\lambda \right) y+\left( -2+4\lambda \right) z+2-8\lambda =0
गोले के केन्द्र के निर्देशांक\left( -\lambda ,-\frac { 7+3\lambda }{ 2 } ,\frac { 2-4\lambda }{ 2 } \right)
गोले के केन्द्र से समतल 2x+3y+4z= 8 पर लम्ब की लम्बाई
\frac { 2\times -\lambda +3\times -\frac { 7+3\lambda }{ 2 } +4\times -\frac { 7+3\lambda }{ 2 } }{ \sqrt { { 2 }^{ 2 }+{ 3 }^{ 2 }+{ 4 }^{ 2 } } } =0
[वृहत वृत्त होने के कारण लम्ब की लम्बाई शून्य होगी]
-2\lambda -\frac { 21 }{ 2 } -\frac { 9\lambda }{ 2 } +4-8\lambda -8=0\\ -2\lambda -\frac { 9\lambda }{ 2 } -8\lambda =\frac { 21 }{ 2 } -\frac { 4 }{ 1 } +\frac { 8 }{ 1 } \\ \frac { -4\lambda -9\lambda -16\lambda }{ 2 } =\frac { 21-8+16 }{ 2 } \\ \frac { -29\lambda }{ 2 } =\frac { 29 }{ 2 } \\ \lambda =-1
समीकरण(1) में मान रखने पर:
{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }-2x+4y-6z+10=0
Question-3.उस गोले का समीकरण ज्ञात करो जिसका वृत्त { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }=16,\quad 2x-3y+6z=7 वृहत्त वृत्त हो। साथ ही वृहत वृत्त की त्रिज्या एवं केन्द्र के निर्देशांक भी ज्ञात कीजिए।
(Find the equation of the sphere having the circle{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }=16,\quad 2x-3y+6z=7 as a great circle.Also find the radius and centre of the great circle.)
Solution-वृहत वृत्त का समीकरण-{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }=16,\quad 2x-3y+6z=7
गोले का समीकरण-{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }-16+\lambda \left( 2x-3y+6z-7 \right) =0....(1)\\ { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2\lambda x-3\lambda y+6\lambda z-16-7\lambda =0
गोले के केन्द्र के निर्देशांक=\left( -\lambda ,\frac { 3\lambda }{ 2 } ,-3\lambda \right)
गोले के केन्द्र \left( -\lambda ,\frac { 3\lambda }{ 2 } ,-3\lambda \right) से समतल 2x-3y+6z=7 पर लम्ब की लम्बाई=
\frac { 2\times \left( -\lambda \right) -3\times -\frac { 3\lambda }{ 2 } +6\times -3\lambda }{ \sqrt { { 2 }^{ 2 }+{ \left( -3 \right) }^{ 2 }+{ \left( 6 \right) }^{ 2 } } } =0
[वृहत वृत्त होने के कारण लम्ब की लम्बाई शून्य होगी]
-2\lambda -\frac { 9\lambda }{ 2 } -18\lambda -7=0\\ \frac { -4\lambda -9\lambda -36\lambda -14 }{ 2 } =0\\ -49\lambda =14\\ \lambda =-\frac { 14 }{ 49 } \\ \lambda =-\frac { 2 }{ 7 }
अतः गोले का समीकरण ज्ञात करने हेतु उपर्युक्त मान समीकरण (1) में रखने पर-
{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }-16-\frac { 2 }{ 7 } \left( 2x-3y+6z-7 \right) =0\\ { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }-16-\frac { 1 }{ 7 } \left( 4x-6y+12z-14 \right) =0
वृहत वृत्त की त्रिज्या=गोले की त्रिज्या
==\sqrt { { u }^{ 2 }+{ v }^{ 2 }+{ w }^{ 2 }-c } \\ =\sqrt { { \left( -\frac { 2 }{ 7 } \right) }^{ 2 }+{ \left( \frac { 3 }{ 7 } \right) }^{ 2 }+{ \left( -\frac { 6 }{ 7 } \right) }^{ 2 }+14 } \\ =\sqrt { \frac { 4 }{ 49 } +\frac { 9 }{ 49 } +\frac { 36 }{ 49 } +14 } \\ =\sqrt { 1+14 } \\ =\sqrt { 15 }
केन्द्र के निर्देशांक=\left( \frac { 2 }{ 7 } ,-\frac { 1 }{ 7 } ,\frac { 6 }{ 7 } \right)
Question-4.सिद्ध कीजिए कि समतल x+2y-z=4 गोले { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }-x+z-2=0को एक इकाई त्रिज्या के वृत्त में काटता है और उस गोले का समीकरण ज्ञात कीजिए जिसका यह वृत्त एक वृहत वृत्त हो।
(Prove that the plane x+2y-z=4 cuts the sphere { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }-x+z-2=0in a circle of radius unity and find the equation of the sphere which has this circle as one of its great circle.)
Solution-गोले का समीकरण-
{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }-x+z-2=0
केन्द्र के निर्देशांक\left( \frac { 1 }{ 2 } ,0,-\frac { 1 }{ 2 } \right)
समतल x+2y-z=4 पर लम्ब की लम्बाई
p=\left| \frac { \frac { 1 }{ 2 } +2\times 0-\left( -\frac { 1 }{ 2 } \right) -4 }{ \sqrt { { 1 }^{ 2 }+{ 2 }^{ 2 }+{ \left( -1 \right) }^{ 2 } } } \right| \\ p=\left| \frac { \frac { 1 }{ 2 } +\frac { 1 }{ 2 } -4 }{ \sqrt { 1+4+1 } } \right| \\ p=\frac { 3 }{ \sqrt { 6 } }
गोले की त्रिज्या r=\sqrt { { \left( -\frac { 1 }{ 2 } \right) }^{ 2 }+{ 0 }^{ 2 }+{ \left( \frac { 1 }{ 2 } \right) }^{ 2 }+2 } \\ r=\sqrt { \frac { 1 }{ 4 } +\frac { 1 }{ 4 } +2 } \\ r=\sqrt { \frac { 10 }{ 4 } } =\sqrt { \frac { 5 }{ 2 } }
वृत्त की त्रिज्या R=\sqrt { { r }^{ 2 }-{ p }^{ 2 } } \\ R=\sqrt { \frac { 5 }{ 2 } -{ \left( \frac { 3 }{ \sqrt { 6 } } \right) }^{ 2 } } \\ R=\sqrt { \frac { 5 }{ 2 } -\frac { 3 }{ 6 } } =\sqrt { \frac { 15-9 }{ 6 } } =1
माना गोले का समीकरण-
{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }-x+z-2+\lambda \left( x+2y-z-4 \right) =0\\ { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+x\left( -1+\lambda \right) +2\lambda y+\left( 1-\lambda \right) -2-4\lambda =0.....(1)
गोले के केन्द्र के निर्देशांक=\left( \frac { 1-\lambda }{ 2 } ,-\lambda ,\frac { \lambda -1 }{ 2 } \right)
समतल x+2y-z=4 पर केन्द्र\left( \frac { 1-\lambda }{ 2 } ,-\lambda ,\frac { \lambda -1 }{ 2 } \right) से लम्ब की लम्बाई
\frac { \frac { 1-\lambda }{ 2 } -2\lambda +\frac { 1-\lambda }{ 2 } -4 }{ \sqrt { { 1 }^{ 2 }+{ 2 }^{ 2 }+{ \left( -1 \right) }^{ 2 } } } =0\\ -3\lambda =3\\ \lambda =-1
का मान समीकरण (1) में रखने पर-
{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }-2x-2y+2z+2=0
उपर्युक्त उदाहरणों से व्यास रूप में गोले का समीकरण (Diameter form of equation of sphere) को समझा जा सकता है।
Also Read This Article:-Perpendicular length pole on tangent
2.व्यास रूप में गोले का समीकरण (Diameter form of equation of sphere) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.एक गोले के लिए समीकरण क्या है? (What is the equation for a sphere?):
उत्तर:एक गोले का व्यापक समीकरण है (The general equation of a sphere is):(x – a)²+(y – b)²+(z – c)²=r² जहां (a, b, c) गोले के केंद्र का प्रतिनिधित्व करता है,r त्रिज्या का प्रतिनिधित्व करता है और x, y, और z गोले की सतह पर स्थित बिंदुओं के निर्देशांक हैं।
प्रश्न:2.आप एक गोले का व्यास कैसे ज्ञात करते हैं? (How do you find diameter of a sphere?):
उत्तर:एक गोले का व्यास निम्नलिखित समीकरणों से ज्ञात किया जा सकता है:
गोले का व्यास दी गई त्रिज्या के साथ (Diameter of a sphere With given radius):d =2r गोले का व्यास दिए गए व्यास के साथ (Diameter of a sphere With given diameter):d = √(A/π) गोले का व्यास दिए गए आयतन के साथ (Diameter of a sphere With given volume):d = ³√(6V/π) ।
प्रश्न:3.क्या किसी गोले का व्यास होता है? (Does a sphere have a diameter?):
उत्तर:एक वृत्त या गोले का व्यास त्रिज्या के 2 गुना के बराबर होता है।
प्रश्न:4.क्या एक गोले की लंबाई व्यास है? (Is the length of a sphere the diameter?):
उत्तर:गोले के केंद्र से गुजरने वाली सबसे लंबी सीधी रेखा को गोले का व्यास कहा जाता है।यह गोले की त्रिज्या की लंबाई का दोगुना है।
एक गोले के सूत्र (Sphere Formulas)।
गोले का व्यास (Diameter of a Sphere) D=2r
गोले का पृष्ठीय क्षेत्रफल (Surface Area of a Sphere) A=4π r^2
गोले का आयतन (Volume of a Sphere) V= \frac{4}{3}π r^3
प्रश्न:5.क्या कोई गोला समतल हो सकता है? (Can a sphere be flat?):
उत्तर:एक टोपोलॉजिकल गोला (topological sphere) में एक ज्यामिति हो सकती है जो कि एक सीमित संख्या में बिंदुओं को छोड़कर सपाट (flat) होती है: उदाहरण के लिए,नियमित पॉलीहेड्रा (regular polyhedra) ऐसे गोले होते हैं जो उनके शीर्षों को छोड़कर सपाट होते हैं।स्वयं शीर्षों पर वक्रता (curvature) अनंत हो जाती है,इस प्रकार इसका समाकलन उस शीर्ष पर कोण में कमी (deficit angle) कर देता है।
प्रश्न:6.3d में एक गोले की कितनी भुजाएँ होती हैं? (How many sides does a sphere have in 3d?):
उत्तर: Name\quad\quad Faces\text(फलक)\quad\quad Edges \text(किनारे)
\quad\quad \text गोला\quad\quad\quad\quad 1\quad\quad\quad\quad\quad\quad\quad 0
उपर्युक्त प्रश्नों के उत्तर द्वारा व्यास रूप में गोले का समीकरण (Diameter form of equation of sphere) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |