Equation of Right Circular Cone in 3D
1.3D में लम्बवृत्तीय शंकु का समीकरण (Equation of Right Circular Cone in 3D),मूलबिन्दु पर शीर्ष वाले लम्ब वृत्तीय शंकु का समीकरण (Equation of Right Circular Cone having Vertex at Origin):
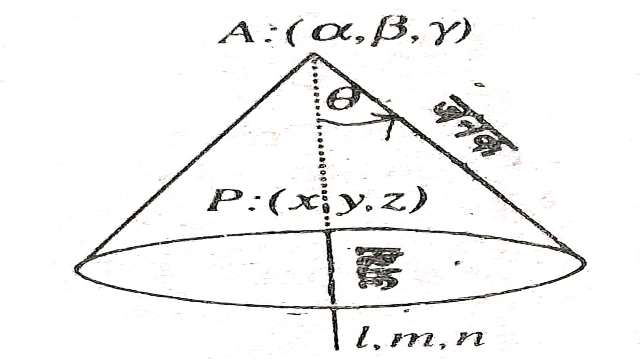
3D में लम्बवृत्तीय शंकु का समीकरण (Equation of Right Circular Cone in 3D) में लम्बवृत्तीय शंकु,शीर्ष व अक्ष को जानना आवश्यक है।एक निश्चित् बिन्दु से गुजरने वाली तथा एक निश्चित् रेखा के साथ नियत कोण (माना \theta) बनाने वाली रेखा द्वारा निर्मित पृष्ठ को लम्बवृत्तीय शंकु कहते हैं।निश्चित् बिन्दु को शंकु का शीर्ष,निश्चित् रेखा को शंकु का अक्ष कहते हैं।जनक,अक्ष के साथ जो नियत कोण \theta बनाता है वह अर्द्धशीर्ष कोण (Semi-vertical angle) कहलाता है।
लम्बवृत्तीय शंकु का समीकरण ज्ञात करना जिसका शीर्ष (\alpha, \beta, \gamma) है।अक्ष \frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n} है तथा अर्द्धशीर्ष कोण \theta है।
(To find the equation of a right circular cone whose vertex is (\alpha, \beta, \gamma),semi vertical angle is \theta and axis is \frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n})
शंकु पर कोई बिन्दु P(x,y,z) लो तब P(x,y,z) तथा शंकु के शीर्ष को मिलाने वाली रेखा के दिक्अनुपात होंगे साथ ही शंकु के अक्ष के दिक्अनुपात l,m,n है तब
\cos \theta=\frac{l(x-\alpha)+m(y-\beta)+n(z-\gamma)}{\sqrt{\left(l^{2}+m^{2}+n^{2}\right)} \sqrt{(x-\alpha)^{2}+(y-\beta)^{2}+(z-\gamma)^{2}}} \\ \Rightarrow \cos ^{2} \theta\left\{(x-\alpha)^{2}+(y-\beta)^{2}+(z-\gamma)^{2}\right\}\left(l^{2}+m^{2}+n^{2}\right)=\left[l(x-\alpha)+m (y-\beta)+n(z-\gamma)\right]^{2}
जो कि लम्बवृत्तीय शंकु का अभीष्ट समीकरण है।
उपप्रमेय (Corollary):1.जब शंकु का शीर्ष मूलबिन्दु हो तब लम्बवृत्तीय शंकु का समीकरण
(l x+m y+n z)^{2}=\cos ^{2} \theta \left(l^{2}+m^{2}+n^{2}\right)\left(x^{2}+y^{2}+z^{2}\right)
उपप्रमेय (Corollary):2.जब शंकु का शीर्ष मूलबिन्दु है तथा अक्ष z-अक्ष है तथा अर्द्धशीर्ष कोण \theta है तब l=0,m=0,n=1
अतः अभीष्ट शंकु का समीकरण होगा:
z^{2}=\cos ^{2} \theta\left(x^{2}+y^{2}+z^{2}\right) \\ \Rightarrow z^{2} \tan ^{2} \theta=x^{2}+y^{2}
इसी प्रकार y^{2}+z^{2}=x^{2} \tan ^{2} \theta तथा z^{2}+x^{2}=y^{2} \tan ^{2} \theta क्रमशः उन शंकुओं के समीकरण हैं जिनके शीर्ष मूलबिन्दु तथा अक्ष x-अक्ष तथा y-अक्ष है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-To Find Equation of Tangent Plane
2.3D में लम्बवृत्तीय शंकु का समीकरण पर आधारित उदाहरण (Examples Based on Equation of Right Circular Cone in 3D):
उस लम्बवृत्तीय शंकु का समीकरण ज्ञात कीजिए जिसका शीर्ष,अक्ष एवं अर्द्धशीर्ष कोण क्रमशः निम्न प्रकार से है:
(Find the equation of a right circular cone whose vertex,axis and semi-vertical angle are respectively as follows:) (From Example 1 to 4):
Example:1.(3,2,1);\frac{x-3}{4}=y-2=\frac{z-1}{3} ; \frac{\pi}{6}
Solution:-अक्ष \frac{x-3}{4}=y-2=\frac{z-1}{3}
शंकु के अक्ष की दिक्अनुपात 4,1,3 है।शंकु के पृष्ठ पर कोई बिन्दु R (x,y,z) लो तब PR के दिक्अनुपात x-3,y-2,z-1 होंगे।चूँकि अर्द्धशीर्ष कोण \frac{\pi}{6} है इसलिए
\cos \frac{\pi}{6}=\frac{4(x-3)+1(y-2)+3(z-1)}{\sqrt{\left(4^{2}+1^{2}+3^{2}\right)} \sqrt{(x-3)^{2}+(y-2)^{2}+(z-1)^{2}}} \\ \frac{\sqrt{3}}{2}=\frac{4 x-12+y-2+3 z-3}{\sqrt{26} \sqrt{(x-3)^{2}+(y-2)^{2}+(z-1)^{2}}} \\ \Rightarrow \frac{3}{4}=\frac{(4 x+y+3 z-17)^{2}}{26\left[(x-3)^{2}+(y-2)^{2}+(z-1)^{2}\right]} \\ \Rightarrow 39\left[(x-3)^{2}+(y-2)^{2}+(z-1)^{2}\right]=(4 x+y+3 z-17)^{2} \times 2 \\ \Rightarrow 39\left[x^{2}-6 x+9+y^{2}-4 y+4+z^{2}-2 z+1\right]=2[16 x^{2}+y^{2}+8 x y+9 z^{2}-102 z+289+24 x z-136 x+6 y z-34 y] \\ \Rightarrow 39 x^{2}-234 x+351+39 y^{2}-156 y+156+39 z^{2}-78 z+39= \\ 32 x^{2}+2 y^{2}+16 x y+18 z^{2}-204 z+578+48 x z-272 x+12 y z-68 y \\ \Rightarrow 7 x^{2}+37 y^{2}+21 z^{2}-16 x y-12 y z-48 z x +48 x-88 y+126 z-32=0
Example:2. (1,-2,-1) ; \frac{x-1}{3}=\frac{y+2}{-4}=\frac{z+1}{3} ; 60^{\circ}
Solution:-अक्ष \frac{x-1}{3}=\frac{y+2}{-4}=\frac{z+1}{3}
शंकु के अक्ष की दिक्अनुपात 3,-4,3 है।शंकु के पृष्ठ पर कोई बिन्दु R (x,y,z) लो तब PR के दिक्अनुपात x-1,y+2,z+1 होंगे।चूँकि अर्द्धशीर्ष कोण 60° है इसलिए
\cos 60^{\circ}=\frac{3(x-1)-4(y+2)+3(z+1)}{\sqrt{(3)^{2}+(-4)^{2}+(3)^{2}}\sqrt{(x-1)^{2}+(y+2)^{2}+(z+1)^{2}}} \\ \frac{1}{2}=\frac{3 x-3-4 y-8+3 z+3}{\sqrt{9+16+9} \sqrt{(x-1)^{2}+(y+2)^{2}+(z+1)^{2}}} \\ \Rightarrow \frac{1}{2}=\frac{3 x-4 y+3 z-8}{\sqrt{34} \sqrt{(x-1)^{2}+(y+2)^{2}+(z+1)^{2}}} \\ \Rightarrow \frac{1}{4}=\frac{(3 x-4 y+3 z-8)^{2}}{34\left[(x-1)^{2}+(y+2)^{2}+(z+1)^{2}\right]} \\ \Rightarrow 17\left[(x-1)^{2}+(y+2)^{2}+(z+1)^{2}\right]=2[3 x-4 y+3 z-8]^{2} \\ \Rightarrow 17\left[x^{2}-2 x+1+y^{2}+4 y+4+z^{2}+2 z+1\right] =2(9 x^{2}+16 y^{2}-24 x y+9 z^{2}+64-48 z+18 x z-48 x-24 y z+64 y) \\ \Rightarrow 17 x^{2}-34 x+17 y^{2}+68 y+17 z^{2}+34 z+102=18 x^{2}+32 y^{2}-48 x y+18 z^{2}+128-96 z+36 x z-96 x-48 y z+128 y \\ \Rightarrow x^{2}+14 y^{2}+z^{2}-48 x y+36 x z -48 y z-62 x+60 y-130 z+26=0
Example:3.(1,1,1) ; \frac{x-1}{-1}=\frac{y-1}{2}=\frac{z-1}{3}; 30^{\circ}
Solution:-अक्ष \frac{x-1}{-1}=\frac{y-1}{2}=\frac{z-1}{3}
शंकु के अक्ष की दिक्अनुपात -1,2,3 है।शंकु के पृष्ठ पर कोई बिन्दु R (x,y,z) लो तब PR के दिक्अनुपात x-1,y-1,z-1 होंगे।चूँकि अर्द्धशीर्ष कोण 30° है इसलिए
\cos 30^{\circ}=\frac{-1(x-1)+2(y-1)+3(z-1)}{\sqrt{(-1)^{2}+(2)^{2}+(3)^{2}} \sqrt{(x-1)^{2}+(y-1)^{2}+(z-1)^{2}}} \\ \Rightarrow \frac{\sqrt{3}}{2}=\frac{-x+1+2 y-2+3 z-3}{\sqrt{1+4+9} \sqrt{(x-1)^{2}+(y-1)^{2}+(z-1)^{2}}} \\ \Rightarrow \frac{\sqrt{3}}{2}=\frac{-x+2 y+3 z-4}{\sqrt{14} \sqrt{(x-1)^{2}+(y-1)^{2}+(z-1)^{2}}} \\ \Rightarrow \frac{3}{4}=\frac{(-x+2 y+3 z-4)^{2}}{14\left[(x-1)^{2}+(y-1)^{2}+(z-1)^{2}\right]} \\ \Rightarrow 21\left[(x-1)^{2}+(y-1)^{2}+(z-1)^{2}\right]=2(x+2 y+3 z-4)^{2} \\ \Rightarrow 21\left[x^{2}-2 x+1+y^{2}-2 y+1+z^{2}-2 z+1\right] =2(x^{2}-4 x y+4 y^{2}+9 z^{2}+16-24 z-6 x z+8 x+12 y z-16 y) \\ \Rightarrow 21 x^{2}-42 x+21 y^{2}-42 y+21 z^{2}-42 z+63=2 x^{2}-8 x y+8 y^{2}+18 z^{2}+32-48 z -12 x z+16 x+24 y z-32 y \\ \Rightarrow 19 x^{2}+13 y^{2}+3 z^{2}+8 x y-24 y z+12 x z-58 x-10 y+6 z+31=0
Example:4.(0,0,0);\frac{x}{1}=\frac{y}{1}=\frac{z}{2} ; 60^{\circ}
Solution:-अक्ष \frac{x}{1}=\frac{y}{1}=\frac{z}{2}
शंकु के अक्ष की दिक्अनुपात 1,1,2 है।शंकु के पृष्ठ पर कोई बिन्दु R (x,y,z) लो तब PR के दिक्अनुपात x,y,z होंगे।चूँकि अर्द्धशीर्ष कोण 60° है इसलिए
\cos 60^{\circ}=\frac{1(x)+1(y)+2(z)}{\sqrt{(1)^{2}+(1)^{2}+(2)^{2}} \sqrt{x^{2}+y^{2}+z^{2}}} \\ \Rightarrow \frac{1}{2}=\frac{x+y+2 z}{\sqrt{1+1+4} \sqrt{x^{2}+y^{2}+z^{2}}} \\ \Rightarrow \frac{1}{4}=\frac{(x+y+2 z)^{2}}{(6)\left(x^{2}+y^{2}+z^{2}\right)} \\ \Rightarrow 3\left(x^{2}+y^{2}+z^{2}\right) =2(x+y+2 z)^{2} \\ \Rightarrow 3 x^{2}+3 y^{2}+3 z^{2}=2 (x^{2}+y^{2}+4 z^{2}+2 x y+4 yz+4x z) \\ \Rightarrow 3 x^{2}+3 y^{2}+3 z^{2}=2 x^{2}+2 y^{2} +8 z^{2}+4 x y+8 y z+8 x z \\ x^{2}+y^{2}-5z^{2}-4 xy-8yz-8xz=0
Example:5.सिद्ध कीजिए कि x^{2}-y^{2}+z^{2}-2 x+4 y+6 z+6=0 एक लम्बवृत्तीय शंकु को निरूपित करता है जिसका शीर्ष (1,2,-3) जिसका अक्ष OY के समान्तर है तथा जिसका अर्द्धशीर्ष कोण 45° है।
(Prove that x^{2}-y^{2}+z^{2}-2 x+4 y+6 z+6=0 represents a right circular cone whose vertex is the point (1,2,-3) whose axis is parallel to OY and whose semi-vertical angle is 45°.)
Solution:अक्ष,OY के समान्तर है अतः अक्ष के दिक्अनुपात 0,1,0 है।यदि पृष्ठ पर कोई बिन्दु R (x,y,z) है तब PR के दिक्अनुपात x-1,y-2,z+3 होंगे।चूँकि अर्द्धशीर्ष कोण 45° है इसलिए
\cos 45=\frac{0(x-1)+1(y-2)+0(z+3)}{\sqrt{0^{2}+1^{2}+0^{2}} \sqrt{(x-1)^{2}+(y-2)^{2}+(z+3)^{2}}} \\ \Rightarrow \frac{1}{\sqrt{2}}=\frac{y-2}{\sqrt{(x-1)^{2}+(y-2)^{2}+(z+3)^{2}}} \\ \Rightarrow \frac{1}{2}=\frac{(y-2)^{2}}{(x-1)^{2}+(y-2)^{2}+(z+3)^{2}} \\ \Rightarrow(x-1)^{2}+(y-2)^{2}+(z+3)^{2}=2(y-2)^{2} \\ x^{2}-2 x+1+y^{2}-4 y+4+z^{2}+6 z+9=2 y^{2}-8 y+8 \\ \Rightarrow x^{2}-y^{2}+z^{2}-2 x+4 y+6 z+6=0
Example:6.लम्बवृत्तीय शंकु का समीकरण ज्ञात कीजिए जिसका शीर्ष मूलबिन्दु है तथा वक्र x^{2}+y^{2} +z^{2}=a^{2} ,z=\frac{a}{2} इसका आधार है।साथ ही बिन्दु \left(0, \frac{\sqrt{3} a}{2}, \frac{a}{2}\right) पर शंकु का स्पर्शतल ज्ञात कीजिए।
(Find the equation to right circular cone having origin as its vertex and curve x^{2}+y^{2} +z^{2}=a^{2} ,z=\frac{a}{2} as its base.Also find the equation to the tangent plane at the point \left(0, \frac{\sqrt{3} a}{2}, \frac{a}{2}\right).)
Solution:शंकु जिसका शीर्ष मूलबिन्दु है तथा आधार x^{2}+y^{2}+z^{2}=a^{2},z=\frac{a}{2} है।अतः इसकी सहायता से समघात बनाकर शंकु का समीकरण प्राप्त किया जा सकता है।
x^{2}+y^{2}+z^{2}=(2 z)^{2} \\ \Rightarrow 2 x^{2}+y^{2}+z^{2}=4 z^{2} \\ \Rightarrow x^{2}+y^{2}-3 z^{2}=0
स्पर्शतल का समीकरण:
x(a \alpha+h \beta+g \gamma)+y(h \alpha+b \beta+f \gamma)+z(g \alpha+f \beta+c \gamma)=0
दिए हुए शंकु से:
a=1,b=1,c=-3 तथा f=g=h=0
\Rightarrow x(0)+y\left(\frac{\sqrt{3}}{2} a\right)+z(\frac{-3 a}{2})=0 \\ \Rightarrow \sqrt{3} a y-3 a z=0 \\ \Rightarrow y-\sqrt{3} z=0Example:7.यदि किसी लम्बवृत्तीय शंकु का शीर्ष मूलबिन्दु है,अक्ष की दिक्कोज्याएँ \cos \alpha, \cos \beta,\cos \gamma हैं तथा अर्द्धशीर्ष कोण \theta है तो सिद्ध करो कि इसका समीकरण होगा:
(If the vertex of a right circular cone is origin and d.c.’s of the axis are \cos \alpha, \cos \beta,\cos \gamma and semi-vertical angle is \theta then prove that its equation is)
(y \cos \gamma-z \cos \beta)^{2}+(z \cos \alpha-x \cos \gamma)^{2}+ (x \cos \beta-y \cos \alpha)^{2}=\left(x^{2}+y^{2}+z^{2}\right)\left(\sin ^{2} \theta\right)
Solution:अक्ष की दिककोज्याएँ \cos \alpha, \cos \beta,\cos \gamma हैं।यदि शंकु के पृष्ठ पर R (x,y,z) है तो PR के दिक्अनुपात x,y,z हैं।अर्द्धशीर्ष कोण \theta है तो:
\Rightarrow \left(x^{2}+y^{2}+z^{2}\right) \left(\cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma\right) \sin^{2} \theta =(y \cos \gamma-z \cos \beta)^{2}+\left(z \cos \alpha-x \cos \gamma \right)^{2}+(x \cos \beta-y \cos \alpha)^{2}
Example:8.उस लम्बवृत्तीय शंकु का समीकरण ज्ञात कीजिए जिसका शीर्ष मूलबिन्दु है अक्ष x=y=z है और उसकी एक जनक रेखा 2x=3y=-5z है।
(Find the equation to the right circular cone having vertex at the origin,axis x=y=z and one of the generators is the line 2x=3y=-5z.)
Solution:अक्ष के दिक्अनुपात 1,1,1 है।जनक रेखा \frac{x}{\frac{1}{2}}=\frac{y}{\frac{1}{3}}=\frac{z}{-\frac{1}{5}} है।यदि अर्द्धशीर्ष कोण \theta है तो
\cos \theta=\frac{\frac{1}{2}(1)+\frac{1}{3}(1)-\frac{1}{5} \times 1}{\sqrt{(1)^{2}+(1)^{2}+(1)^{2}} \sqrt{\left(\frac{1}{2}\right)^{2}+(\frac{1}{3})^{2}+(-\frac{1}{5})^{2}}} \\ =\frac{\frac{1}{2}+\frac{1}{3}-\frac{1}{5}}{\sqrt{3} \sqrt{\frac{1}{4}+\frac{1}{9}+\frac{1}{25}}} \\ =\frac{\frac{15+10-6}{30}}{\sqrt{3} \sqrt{\frac{1}{4}+\frac{1}{9}+\frac{1}{25}}} \\ =\frac{\frac{19}{30}}{\sqrt{3} \sqrt{\frac{225+100+36}{900}}} \\ =\frac{19}{\sqrt{3} \sqrt{361}} \\ \Rightarrow \cos \theta =\frac{1}{\sqrt{3}} \cdots(1)
शंकु के पृष्ठ पर R (x,y,z) कोई बिन्दु है तो PR के दिक्अनुपात x,y,z होंगे।इसलिए
\cos \theta=\frac{1 \cdot x+1 \cdot y+1 \cdot z}{\sqrt{1^{2}+1^{2}+1^{2}} \sqrt{x^{2}+ y^{2}+z^{2}}} \\ \cos \theta=\frac{x+y+z}{\sqrt{3} \sqrt{x^{2}+y^{2}+z^{2}}} \cdots(2)
(1) व (2) से:
\frac{x+y+z}{\sqrt{3} \sqrt{x^{2}+y^{2}+z^{2}}}=\frac{1}{\sqrt{3}} \\ \Rightarrow (x+y+z)^{2}= x^{2}+y^{2}+z^{2} \\ \Rightarrow 2 x y+2 y z+2 z x=0 \\ \Rightarrow x y+y z+z x=0
Example:9.लम्बवृत्तीय शंकु का समीकरण ज्ञात कीजिए जो (1,1,1) से गुजरे तथा जिसका शीर्ष (1,0,1) तथा शंकु का अक्ष निर्देशाक्षों से बराबर-बराबर कोण बनाता है।
(Find the equation to the right circular cone passing through (1,1,1) and having the vertex at the point (1,0,1). The axis of the cone is equally inclined to the co-ordinate axes.)
Solution:शीर्ष P (1,0,1),माना शंकु के पृष्ठ पर कोई बिन्दु R (x,y,z) है तब PR के दिक्अनुपात x-1,y,z-1 है।अक्ष की दिक्कोज्या \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} है तथा अर्द्धशीर्ष कोण \theta है तो:
\cos \theta=\frac{\frac{1}{\sqrt{3}}(x-1)+\frac{1}{\sqrt{3}} y+\frac{1}{\sqrt{3}}(z-1)}{\sqrt{\left(\frac{1}{\sqrt{3}}\right)^{2}+\left(\frac{1}{\sqrt{3}}\right)^{2}+\left(\frac{1}{\sqrt{3}}\right)^{2}} \sqrt{(x-1)^{2}+ y^{2} +(z-1)^{2}}} \\ \Rightarrow \cos \theta=\frac{\frac{1}{\sqrt{3}}(x-1)+\frac{y}{\sqrt{3}}+\frac{1}{\sqrt{3}}(z-1)}{\sqrt{(x-1)^{2}+y^{2}+(z-1)^{2}}} \cdots(1)
यदि शंकु (1,1,1) से गुजरे तो:
\cos \theta=\frac{1}{\sqrt{3}} \cdots(2)
(1) व (2) से:
\frac{1}{\sqrt{3}}= \frac{(x-1)+y+z-1}{\sqrt{3} \sqrt{(x-1)^{2}+y^{2}+(z-1)^{2}}} \\ \Rightarrow (x-1)^{2}+y^{2}+(z-1)^{2}=(x+y+z-2)^{2} \\ \Rightarrow x^{2}+2 x+1+y^{2}+z^{2}-2 z+1=x^{2} +y^{2}+z^{2}+4+2 x y-4 z+2 x z-4 x+2 y z-4 y \\ \Rightarrow 2 x y+2 x z+2 y z-2 x-2 z-4 y+2=0 \\ \Rightarrow x y+x z+y z-x-2 y-z+1=0
Example:10.उस लम्बवृत्तीय शंकु का समीकरण ज्ञात कीजिए जिसका शीर्ष (0,0,0),अक्ष OX तथा अर्द्धशीर्ष कोण \alpha है।
(Find the equation of the right circular cone whose vertex is (0,0,0), axis is OX and semi-vertical angle is \alpha.)
Solution:अक्ष OX है अतः अक्ष के दिक्अनुपात 1,0,0 हैं।माना कि शंकु के पृष्ठ पर बिन्दु R (x,y,z) है तो PR के दिक्अनुपात x-0,y-0,z-0 होंगे।अर्द्धशीर्ष कोण \alpha है अतः
\cos \alpha=\frac{1 \cdot x+0 \cdot y+0 \cdot z}{\sqrt{1^{2}+0^{2}+0^{2}} \sqrt{x^{2}+y^{2}+z^{2}}} \\ \Rightarrow \left(x^{2}+y^{2}+z^{2}\right) \cos ^{2} \alpha=x^{2}
Example:11.सिद्ध कीजिए कि उस शंकु का समीकरण जो कि रेखा \frac{x}{l}=\frac{y}{m}=\frac{z}{n} को रेखा \frac{x}{a}=\frac{y}{b}=\frac{z}{c} (शंकु का अक्ष लेते हुए) के परित: घुमाने पर जनित होता है, निम्न है:
(Show that the equation of the cone generated by rotating the line \frac{x}{l}=\frac{y}{m}=\frac{z}{n} about the line \frac{x}{a}=\frac{y}{b}=\frac{z}{c} as axis is)
\left(l^{2}+m^{2}+n^{2}\right)(a x+b y+c z)^{2}=(a l+b m+c n)^{2}\left(x^{2}+y^{2}+z^{2}\right)
Solution:शंकु का अक्ष: \frac{x}{a}=\frac{y}{b}=\frac{z}{c}
अतः अक्ष के दिक्अनुपात a,b,c हैं।यदि शंकु के पृष्ठ पर R (x,y,z) कोई बिन्दु है तो PR के दिक्अनुपात x,y,z हैं।अर्द्धशीर्ष कोण \theta है तो:
\cos \theta=\frac{a x+b y+c z}{\sqrt{a^{2}+b^{2}+c^{2}} \sqrt{x^{2}+y^{2}+z^{2}}} \cdots(1)
जनक रेखा के दिक्अनुपात l,m,n है अतः
\cos \theta=\frac{a l+b m+c n}{\sqrt{a^{2}+b^{2}+c^{2}} \sqrt{l^{2}+m^{2}+n^{2}}} \cdots(2)
(1) व (2) से:
\frac{a x+b y+c z}{\sqrt{a^{2}+b^{2}+c^{2}} \sqrt{x^{2}+y^{2}+z^{2}}}=\frac{a l+b m+c n}{\sqrt{a^{2}+b^{2}+c^{2}} \sqrt{l^{2}+m^{2}+n^{2}}} \\ \Rightarrow (a x+b y+c z)^{2}\left(l^{2} +m^{2}+n^{2}\right)=(al+b m+c x)^{2}\left(x^{2}+y^{2}+z^{2}\right)
Example:12.उस लम्बवृत्तीय शंकु का समीकरण ज्ञात करो जो सरल रेखा 2x+3y=0,z=0 को y-अक्ष के परित: घुमाने पर प्राप्त होता है।
(Find the equation to the cone formed by roating the line 2x+3y=0,z=0 about the y-axis.)
Solution:अक्ष y-अक्ष है जिसके दिक्अनुपात 0,1,0 हैं।जनक रेखा की समीकरण 2x+3y=0,z=0 है।
\frac{x}{3}=\frac{y-2}{-2}=\frac{z}{0} \cdots(1)
y-अक्ष का प्रतिच्छेदन बिन्दु x=0,z=0 तथा जनक रेखा (1), (0,2,0) से गुजरती है अतः शीर्ष के निर्देशांक (0,2,0) हैं।अर्द्धशीर्ष कोण \theta है तो:
\cos \theta=\frac{0 \cdot 3+1(-2)+0-0}{\sqrt{0^{2}+1^{2}+0^{2}} \sqrt{(3)^{2}+(-2)^{2}+0^{2}}} \\ \cos \theta=\frac{-2}{\sqrt{13}} \cdots(2)
शंकु के पृष्ठ पर बिन्दु R (x,y,z) है तब PR के दिक्अनुपात x,y-2,z
\cos \theta=\frac{0 \cdot x+1 \cdot(y-2)+0 \cdot z}{\sqrt{0^{2}+1^{2}+0^{2}}\sqrt{x^{2}+(y-2)^{2}+z^{2}}} \cdots(3)
(2) व (3) से:
-\frac{2}{\sqrt{13}}=\frac{y-2}{\sqrt{x^{2}+(y-2)^{2}+z^{2}}} \\ \Rightarrow 4\left[x^{2}+(y-z)^{2}+ z^{2}\right]=13(y-2)^{2} \\ \Rightarrow 4 x^{2}-9 y^{2}+y z^{2}+36 y-36=0
उपर्युक्त उदाहरणों के द्वारा 3D में लम्बवृत्तीय शंकु का समीकरण (Equation of Right Circular Cone in 3D),मूलबिन्दु पर शीर्ष वाले लम्ब वृत्तीय शंकु का समीकरण (Equation of Right Circular Cone having Vertex at Origin) को समझ सकते हैं।
3.3D में लम्बवृत्तीय शंकु का समीकरण पर आधारित सवाल (Questions Based on Equation of Right Circular Cone in 3D):
(1.)लम्बवृत्तीय शंकु का समीकरण ज्ञात करो जिसका शीर्ष P (2,-3,5),अक्ष PQ जो निर्देशाक्षों से बराबर-बराबर कोण बनाती है तथा अर्द्धशीर्ष कोण 30° है।
(Find the equation to the right circular cone whose vertex is P (2,-3,5), axis PQ makes equal angles with the coordinate axes and semi-vertical angle is 30°.)
(2.)उस लम्बवृत्तीय शंकु का अर्द्धशीर्ष कोण ज्ञात करो जिसके तीन परस्पर लम्बवत् स्पर्शतल हों।
(Find the semi-vertical angle of right circular cone having a set of three mutually perpendicular tangent planes.)
उत्तर (Answers): (1) 5\left(x^{2}+y^{2}+z^{2}\right)-8(y z+z x+x y)-4 x+86 y-58 z+278=0 \\ (2)\theta=\cot ^{-1}(\sqrt{2})
उपर्युक्त सवालों को हल करने पर 3D में लम्बवृत्तीय शंकु का समीकरण (Equation of Right Circular Cone in 3D),मूलबिन्दु पर शीर्ष वाले लम्ब वृत्तीय शंकु का समीकरण (Equation of Right Circular Cone having Vertex at Origin) को ठीक से समझ सकते हैं।
Also Read This Article:-Condition for Equation Represents Cone
4.3D में लम्बवृत्तीय शंकु का समीकरण (Equation of Right Circular Cone in 3D) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.शंकु का अर्द्धशीर्ष कैसे ज्ञात करते हैं?उदाहरण द्वारा समझाओ।(Explain by example How to find the semi-vertical angle of the cone?):
उत्तर:एक लम्बवृत्तीय शंकु का शीर्ष मूलबिन्दु है तथा अक्ष निर्देशाक्षों से बराबर कोण बनाती है।यदि शंकु का समीकरण 4\left(x^{2}+y^{2}+z^{2}\right)+9(y z+z x+x y)=0 है तो सिद्ध करो कि इसका अर्द्धशीर्ष कोण \cos^{-1} \left(\frac{1}{3 \sqrt{3}}\right) है।
(The axis of a right circular cone, whose vertex is origin,makes equal angles with the co-ordinate axes.If the equation of the cone be,prove that the semi-vertical angle is \cos^{-1} \left(\frac{1}{3 \sqrt{3}}\right).)
Solution:अक्ष की दिककोज्याएँ \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}} हैं।यदि शंकु के पृष्ठ पर R (x,y,z) बिन्दु है तो PR के दिक्अनुपात x,y,z होंगे।अर्द्धशीर्ष कोण \theta है तो:
\cos \theta=\frac{\frac{1}{\sqrt{3}} x+\frac{1}{\sqrt{3}} y+\frac{1}{\sqrt{3}} z}{\sqrt{\left(\frac{1}{\sqrt{3}}\right)^{2}+\left(\frac{1}{\sqrt{3}}\right)^{2}+\left(\frac{1}{\sqrt{3}}\right)^{2}} \sqrt{x^{2}+y^{2}+z^{2}}}\\ =\frac{\frac{1}{\sqrt{3}}(x+y+z)}{\sqrt{x^{2}+y^{2}+z^{2}}} \\ \cos ^{2} \theta=\frac{(x+y+z)^{2}}{3\left(x^{2}+y^{2} +z^{2}\right)} \\ \Rightarrow x^{2}+y^{2}+z^{2}-3 x^{2} \cos ^{2} \theta-3 y^{2} \cos ^{2} \theta- 3 z^{2} \cos ^{2} \theta+2 x y+2 y z+2 z x=0 \\ \Rightarrow \left(1-3 \cos ^{2} \theta\right) x^{2}+\left(1-3 \cos ^{2} \theta\right) y^{2}+\left(1-3 \cos ^{2} \theta\right) z^{2}+2 x y+2 y z+2 z x=0 \cdots(1)
दिए हुए शंकु का समीकरण: 4 x^{2}+4 y^{2}+4 z^{2}+9 y z+9 z x+9 x y=0 \cdots(2)
(1) व (2) के गुणांकों की तुलना करने पर:
\frac{1-3 \cos ^{2} \theta}{4}=\frac{2}{9} \\ \Rightarrow 9-27 \cos ^{2} \theta=8 \\ \Rightarrow 27 \cos ^{2} \theta=1 \Rightarrow \cos ^{2} \theta=\frac{1}{27} \\ \Rightarrow \theta=\cos^{-1} \left(\frac{1}{3 \sqrt{3}}\right)
प्रश्न:2.लम्बवृत्तीय शंकु के समीकरण को ज्ञात करने को उदाहरण द्वारा समझाओ।(Explain by example the equation of a right circular cone):
उत्तर:उस लम्बवृत्तीय शंकु का समीकरण ज्ञात करो जिसकी जनक रेखाएँ मूलबिन्दु से जाती है और तीन बिन्दुओं (1,2,2);(2,1,-2) तथा (2,-2,1) से जाने वाले वृत्त को काटती है।
(Find the equation of the right circular cone generated by straight lines drawn from the origin to cut the circle through the three points (1,2,2);(2,1,-2) and (2,-2,1).)
Solution:माना अक्ष के दिक्अनुपात l,m,n है।शंकु पर कोई बिन्दु R (x,y,z) है तो PR के दिक्अनुपात x,y,z हैं।यदि अर्द्धशीर्ष कोण \theta है तो:
\cos \theta=\frac{l x+m y+n z}{\sqrt{l^{2}+m^{2}+m^{2}} \sqrt{x^{2}+y^{2}+z^{2}}} \cdots(1)
यह (1,2,2);(2,1,-2) तथा (2,-2,1) से गुजरता है अतः
\cos \theta=\frac{l+2 m+2 n}{\sqrt{l^{2}+m^{2}+n^{2}} \sqrt{1^{2}+2^{2}+ 2^{2}}} \\ \cos \theta=\frac{l+2 m+2 n}{3 \sqrt{l^{2}+m^{2}+n^{2}}} \cdots(2) \\ \cos \theta=\frac{2 l+m-2 n}{3 \sqrt{l^{2}+m^{2}+n^{2}}} \cdots(3) \\ \cos \theta=\frac{2 l-2 m+n}{3 \sqrt{l^{2}+m^{2}+n^{2}}} \cdots(4)
(2) व (3) से:
l+2m+2n=2l+m-2n
-l+m+4n=0…..(5)
(3) व (4) से:
m=n….(6)
(5) व (6) से:
l=5n
\frac{l}{5}=\frac{m}{1}=\frac{n}{1} \\ \cos \theta=\frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}}=\frac{5 x+y+z}{\sqrt{27} \sqrt{x^{2}+y^{2}+z^{2}}} \\ 8 x^{2}-4 y^{2}-4 z^{2} +5 x y +y z+5 z x=0
उपर्युक्त प्रश्नों के उत्तर द्वारा 3D में लम्बवृत्तीय शंकु का समीकरण (Equation of Right Circular Cone in 3D),मूलबिन्दु पर शीर्ष वाले लम्ब वृत्तीय शंकु का समीकरण (Equation of Right Circular Cone having Vertex at Origin) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
Equation of Right Circular Cone in 3D
3D में लम्बवृत्तीय शंकु का समीकरण
(Equation of Right Circular Cone in 3D)
Equation of Right Circular Cone in 3D
3D में लम्बवृत्तीय शंकु का समीकरण (Equation of Right Circular Cone in 3D) में लम्बवृत्तीय
शंकु,शीर्ष व अक्ष को जानना आवश्यक है।एक निश्चित् बिन्दु से गुजरने वाली तथा
एक निश्चित् रेखा के साथ नियत कोण