LPP Formulation and Graphical Solution
1.एलपीपी संरूपण तथा आलेखी हल (LPP Formulation and Graphical Solution),रैखिक प्रोग्रामन संरूपण तथा आलेखी विधि (Linear Programming Formulation and Graphical Method):
एलपीपी संरूपण तथा आलेखी हल (LPP Formulation and Graphical Solution):प्रत्येक व्यक्ति के लिए निर्णयन (Decision Making) एक बहुत महत्वपूर्ण परिघटना (Phenomenon) है।जैसे डेयरी फार्म के मालिक की इच्छा रहती है कि किस प्रकार दूध का उत्पादन ज्यादा से ज्यादा हो जबकि उसके पास साधन सीमित हैं।एक सेनाध्यक्ष का सदैव प्रयास रहता है कि सेना का गठन किस प्रकार किया जाए जिससे उसकी आक्रामक शक्ति अधिकतम हो इत्यादि।इस प्रकार की समस्याएं दैनिक जीवन में कई प्रकार की आती हैं जिसमें साधन सीमित होने के पश्चात् भी अनुकूलतम हल समस्यानुसार ज्ञात किया जाता है।
उपर्युक्त प्रकार की परिस्थितियों में समस्या का अनुकूलतम समाधान ज्ञात करने हेतु गणितीय विधि जिसे रैखिक प्रोग्रामन कहते हैं का प्रयोग करते हैं।सन् 1947 में जॉर्ज बी डेन्टजिग,मार्शल वुड तथा उनके साथी जो कि संयुक्त राज्य अमेरिका की वायुसेना के अधिकारी थे,सर्वप्रथम रैखिक प्रोग्राम का संरूपण तथा इसके हल का नियमित कार्य विधि,मारक शक्तियों का अनुकूलतम प्रकार से नियोजन करने के लिए किया था।
चूंकि प्रारंभ में इसका प्रयोग युद्ध में होता था इसलिए प्रारंभ में संक्रिया विज्ञान (Operarion Research) कहा जाता था परंतु वर्तमान युग में संक्रिया विज्ञान के स्थान पर प्रायः रैखिक प्रोग्रामन का प्रयोग किया जाता है।
रैखिक प्रोग्रामन सर्व उत्तम हल ज्ञात करने की एक विशेष प्रकार की बहुत ही उत्तम तकनीक (Technology) है।
इस विधि की महत्ता एवं उपयोगिता के कारणवश इस विधि का प्रयोग व्यापार,उद्योग आदि क्षेत्रों में कई प्रकार के प्रतिबंध विद्यमान रहते हैं,में विस्तृत रूप से होने लगा है।
रैखिक शब्द का प्रयोग दो या दो से अधिक चरों के समानुपातिक संबंध एक रेखा पर दर्शाने के लिए किया जाता है तथा किसी समस्या के हल की योजना को गणितीय मशीन संवेध निर्देश के रूप में लाने की प्रक्रिया तंत्र को प्रोग्रामन कहते हैं।
अतः स्पष्ट है कि रैखिक प्रोग्रामन वह तकनीक है जिसका प्रयोग उन प्रोग्रामन समस्याओं में किया जाता है जिसमें उपलब्ध सीमित साधनों का अनुकूलतम अधिकतम लाभ या निम्नतम लागत देने वाला हल ज्ञात किया जाता है और अब तो स्थिति यह आ गई है कि रैखिक प्रोग्रामन के प्रयोग के बिना व्यापार तथा उद्योग को चलाना जिन पर कई प्रकार के प्रतिबंध विद्यमान होते हैं,बहुत कठिन है।
(1.)रैखिक प्रोग्रामन का वर्णन (Description of L.P.P.):
रैखिक प्रोग्रामन का वर्णन निम्न प्रकार है:
(i)प्रतिबंध या व्यवरोध (Constraint):एक युगपत रैखिक समीकरण अथवा असमिकायें अथवा दोनों का n चरों z= x_{1}, x_{2} , \cdots ,x_{n} का समुच्चय जो कि समस्या के प्रतिबंधों को निरूपित करता है।
(ii) उद्देश्य फलन (Objective Function):वह एक घातीय फलन जो कि रैखिक प्रोग्रामन समस्या के लक्ष्य को व्यक्त करता है उद्देश्य फलन कहलाता है।इस फलन को प्राय: Z से निरूपित करते हैं।Z का अधिकतम या निम्नतम मान ज्ञात करना होता है।
(iii)ऋणेतर प्रतिबंध (Non Negative Restrictions):रैखिक प्रोग्रामन समस्या के उद्देश्य फलन में चर सदैव शुन्य या धनात्मक ही होते हैं अर्थात कभी भी ऋणात्मक नहीं होते हैं।
(2.)रैखिक प्रोग्रामन समस्या का गणितीय स्वरूप(Mathematical Model of L.P.P.):
एक n-चरों को रैखिक प्रोग्रामन समस्या का कुछ प्रतिबंधों सहित प्रक्कथन निम्न प्रकार है:
इष्टतम करो (Optimize) z=a_{1} x_{1}+c_{2} x_{2} +\cdots+c_{n} x_{n} \cdots(1)
प्रतिबन्ध
a_{11} x_{1}+a_{12} x_{2}+a_{13} x_{3}+\cdots++a_{1 n} x_{n} \leq(\text{ या }=\text{ या }\geq ) b_{1}\\ a_{21} x_{1}+a_{22} x_{2}+a_{23} x_{3}+\cdots+a_{2 n} x_{n} \leq(\text{ या }=\text{ या }\geq ) b_{2}\\ a_{31} x_{1}+a_{32} x_{2}+a_{33} x_{3}+\cdots+a_{3 n} x_{n} \leq(\text{ या }=\text{ या }\geq ) b_{3}\\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ a_{m 1} x_{1}+a_{m_{2}} x_{2}+a_{m 3} x_{3}+\cdots+a_{m n} x_{n} \leq(\text{ या }=\text{ या }\geq ) b_{m} \cdots(2)
तथा ऋणेतर प्रतिबन्ध x_{j} \geq 0, j=1,2,\cdots n \quad \cdots(3)
उपर्युक्त (1),(2),(3) में समस्त a_{i j}, b_{j} तथा c_{j} अचर हैं तथा x_{j} चर राशियां हैं।
पृथक-पृथक संकेत पद्धति में रैखिक प्रोग्रामन समस्या के प्रक्कथन अलग-अलग हैं जिनमें कुछ निम्न प्रकार हैं:
(i)इष्टतम करो (Optimize):z=\sum_{j=1}^{n} c_{j} x_{j}
प्रतिबन्ध या व्यवरोध:\sum_{j=1}^{n} a_{i j} x_{j} \leq(\text { या }=\text { या }\geq ) 0, i=1,2, \ldots m
तथा x_{j} \geq 0 \quad j=1,2,3, \cdots, n
(ii)इष्टतम करिए: Z=CX
व्यवरोध A X \leq (\text { या }=\geq) b
तथा x \geq 0 जहाँ C=\left(C_{1}, C_{2}, C_{3}, \ldots C_{n}\right) एक पंक्ति सदिश है।
A=\left [ a_{ij} \right ] गुणांकों का मैट्रिक्स है
b=\left(b_{1}, b_{2}, b_{3} \cdots b_{n}\right) एक स्तम्भ सदिश है
तथा O=(0,0,0,…….,0) एक n विमीय शून्य स्तम्भ सदिश है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Derivative of Length of an Arc
2.एलपीपी संरूपण तथा आलेखी हल के उदाहरण (LPP Formulation and Graphical Solution Examples):
आलेख विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए:
(Solve the Following L.P.P. Graphically):
Example:1.अधिकतम (Max.) z=x_{1}+\frac{1}{2} x_{2}
प्रतिबन्ध (s.t.)
3 x_{1}+2 x_{2} \leq 12 \\ 5 x_{1} \leq 1 \\ x_{1}+x_{2} \geq 8 \\ -x_{1}+x_{2} \geq 4 तथा (and) x_{1}, x_{2} \geq 0
Solution:प्रतिबन्ध रेखाओं के संगत सरल रेखाएं निम्न हैं:
3 x_{1}+2 x_{2}=12 \Rightarrow \frac{x_{1}}{4}+\frac{x_{2}}{6}=1 \\ 5 x_{1}=1 \Rightarrow x_{1}=\frac{1}{5} \\ x_{1}+x_{2}=8 \Rightarrow \frac{x_{1}}{8}+\frac{x_{2}}{8}=1 \\ -x_{1}+x_{2}=4 \Rightarrow \frac{-x_{1}}{4}+\frac{x_{2}}{4}=1 \\ \frac{x_{1}}{4}+\frac{x_{2}}{6}=1 \\ \text { when } x_{1}=0 \text { then } x_{2}=6 \\ \text { when } x_{2}=0 \text { then } x_{1}=4 \\(0,6),(4,0) \\ \frac{x_{1}}{8}+\frac{x_{2}}{8}=1 \\ \text { when } x_{1}=0 \text { then } x_{2}=8 \\ \text { when } x_{2}=0 \text { then } x_{1}=8 \\ (0,8),(8,0) \\ \frac{-x_{1}}{4}+\frac{x_{2}}{4}=1 \\ \text { when } x_{1}=0 \text { then } x_{2}=4 \\ \text { when } x_{2}=0 \text { then } x_{1}=-4 \\ (0,4),(-4,0)
-x_{1}+x_{2}=4 तथा 3 x_{1}+2 x_{2}=12 का प्रतिच्छेद बिन्दु
x_{2}=\frac{24}{5}, x_{1}=\frac{4}{5} \quad A\left(\frac{4}{5}, \frac{24}{5}\right)
x_{1}=\frac{1}{5} तथा 3 x_{1}+2 x_{2}=12 का प्रतिच्छेद बिन्दु
3\left(\frac{1}{5}\right)+2 x_{2}=12 \\ \Rightarrow 2 x_{2}=\frac{12}{1}-\frac{3}{5} \\ \Rightarrow x_{2}=57 \\ B\left(\frac{1}{5}, \frac{57}{10}\right) \\ x_{1}=\frac{1}{5} तथा x_{1}+x_{2}=8 का प्रतिच्छेद बिन्दु
\frac{1}{5}+x_{2}=8 \\ \Rightarrow x_{2}=8-\frac{1}{5}=\frac{39}{5} \\ C\left(\frac{1}{5}, \frac{39}{5}\right)
उपर्युक्त सरल रेखाओं का एक द्विविम चित्र में आरेखण करते हैं तथा प्रत्येक असमिका का हल क्षेत्र निर्धारित करते हैं।इसके पश्चात सभी प्रतिबन्धों की असमिकाओं के क्षेत्रों का उभयनिष्ठ (छायांकित) भाग नहीं हैं।अतः समस्या का कोई सुसंगत हल नहीं है।
Example:2.अधिकतम (Max.)z=4 x_{1}+3 x_{2}
प्रतिबन्ध (s.t.) 2 x_{1}+3 x_{2} \leq 6 \\ -3 x_{1}+2 x_{2} \leq 3 \\ 2 x_{2} \leq 5 \\ 2 x_{1}+x_{2} \leq 4
तथा (and) x_{1}, x_{2} \geq 0
Solution:प्रतिबन्ध रेखाओं के संगत सरल रेखाएं निम्न हैं:
2 x_{1}+3 x_{2}=6 \Rightarrow \frac{x_{1}}{3}+\frac{x_{2}}{2}=1 \\ -3 x_{1}+2 x_{2}=3 \Rightarrow \frac{-x_{1}}{1}+\frac{x_{2}}{\frac{3}{2}}=1 \\ 2 x_{2}=5 \Rightarrow x_{2}=\frac{5}{2} \\ 2 x_{1}+x_{2}=4 \Rightarrow \frac{x_{1}}{2}+\frac{x_{2}}{4}=1 \\ \frac{x_{1}}{3}+\frac{x_{2}}{2}=1 \\ \text { when } x_{1}=0 \text { then } x_{2}=2 \\ \text { when } x_{2}=0 \text { then } x_{1}=3 \\ (0,2),(3,0) \\ -\frac{x_{1}}{1}+\frac{x_{2}}{\frac{3}{2}}=1 \\ \text { when } x_{1}=0 \text { then } x_{2}= \frac{3}{2} \\ \text { when } x_{2}=0 \text { then } x_{1}=-1 \\ \left(0, \frac{3}{2}\right),(-1,0) \\ \frac{x_{1}}{2}+\frac{x_{2}}{4}=1 \\ \text{ When } x_{1}=0 \text{ then } x_{2}=4 \\ \text{ When } x_{2}=0 \text{ then } x_{1}=2 \\ (0,4),(2,0) \\ 2 x_{1}+3 x_{2}=6 तथा -3 x_{1}+2 x_{2}=3 का प्रतिच्छेद बिन्दु
C \left(\frac{3}{13} ,\frac{24}{13}\right) \\ 2 x_{1}+3 x_{2}=6 तथा 2 x_{1}+x_{2}=4 का प्रतिच्छेद बिन्दु
x_{2}=1, x_{1}=\frac{3}{2} \\ B\left(\frac{3}{2}, 1\right)\\ x_{2}=\frac{5}{2} तथा 2 x_{1}+3 x_{2}=6 का प्रतिच्छेद बिन्दु
\left ( -\frac{3}{4},\frac{5}{2} \right )
उपर्युक्त सरल रेखाओं का एक द्विविम चित्र में आरेखण करते हैं तथा प्रत्येक असमिका का हल क्षेत्र निर्धारित करते हैं।इसके पश्चात सभी प्रतिबन्धों की असमिकाओं का उभयनिष्ठ हल क्षेत्र OACBD (छायांकित) समस्या का सुसंगत हल क्षेत्र प्राप्त होता हैं।बहुभुज के किसी एक शीर्ष पर इष्टतम हल प्राप्त होता है।
अब बहुभुज OACBD क्षेत्र के शीर्षों के निर्देशांक निम्न हैं:
O(0,0),A(2,0),B(\frac{3}{2},1),C(\frac{3}{13},\frac{24}{13}),D(0,\frac{3}{2})
उपर्युक्त शीर्षों पर उद्देश्य फलन Z में निर्देशांक प्रतिस्थापित कर इष्टतम हल की परिकलना निम्न है:
| शीर्ष | निर्देशांक | उद्देश्य फलन Z का मान |
| z=4 x_{1}+3 x_{2} | ||
| O | (0,0) | 4(0)+3(0)=0 |
| A | (2,0) | (2)(4)+3(0)=8 |
| B | (\frac{3}{2},1) | 4 \times \frac{3}{2}+3 \times 1=9 |
| C | (\frac{3}{13},\frac{24}{13}) | 4 \times \frac{3}{13}+3 \times \frac{24}{13}=\frac{84}{13} |
| D | (0,\frac{3}{2}) | 4 \times 0+3 \times \frac{3}{2}=\frac{9}{2} |
उपर्युक्त तालिका से स्पष्ट है कि उद्देश्य फलन Z का इष्टतम मान B पर प्राप्त होता है।अत: समस्या का इष्टतम हल है:
x_{1}=\frac{3}{2}, x_{2}=1 तथा Max. Z=9
Example:3.अधिकतम (Max.)z=5 x_{1}+7 x_{2}
प्रतिबन्ध (s.t.) x_{1}+x_{2} \leq 4 \\ 3 x_{1}+8 x_{2} \leq 24 \\ 10 x_{1}+7 x_{2} \leq 35
तथा (and)x_{1}, x_{2} \geq 0
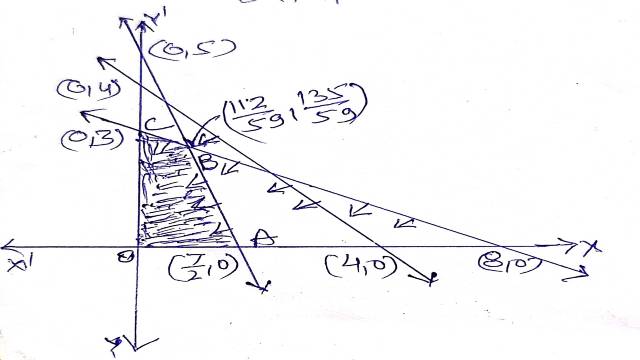
Solution:प्रतिबन्ध रेखाओं के संगत सरल रेखाएं निम्न हैं:
x_{1}+x_{2}=4 \Rightarrow \frac{x_{1}}{4}+\frac{x_{2}}{4}=1 \\ 3 x_{1}+8 x_{2}=2 4 \Rightarrow \frac{x_{1}}{8}+\frac{x_{2}}{3}=1 \\ 10 x_{1}+7 x_{2}=35 \Rightarrow \frac{x_{1}}{\frac{7}{2}}+\frac{x_{2}}{5}=1 \\ \frac{x_{1}}{4} +\frac{x_{2}}{4}=1 \\ \text { When } x_{1}=0 \text { then } x_{2}=4 \\ \text { when } x_{2}=0 \text { then } x_{1}=4 \\ (0,4),(4,0) \\ \frac{x}{8}+\frac{x_{2}}{2}=1 \\ \text { when } x_{1}=0 \text { then } x_{2}=3 \\ \text { when } x_{2}=0 \text { then } x_{1}=8 \\ (0,3), \quad (8,0) \\ \frac{x_{1}}{\frac{7}{2}}+\frac{x_{2}}{5}=1 \\ \text { when } x_{1}=0 \text { then } x_{2}=5 \\ \text { when } x_{2}=0 \text { then } x_{1}=\frac{7}{2} \\ \left(0,5\right), \left(\frac{7}{2}, 0 \right) \\ x_{1}+x_{2}=4 तथा 3 x_{1}+8 x_{2}=24 का प्रतिच्छेद बिन्दु
(\frac{8}{5},\frac{12}{5}) \\ 3 x_{1}+8 x_{2}=24 तथा 10 x_{1}+7 x_{2}=35 का प्रतिच्छेद बिन्दु \left(\frac{112}{59}, \frac{135}{59}\right) \\ x_{1}+x_{2}=4 तथा 10 x_{1}+7 x_{2}=35 का प्रतिच्छेद बिन्दु (\frac{7}{3},\frac{5}{3})
उपर्युक्त सरल रेखाओं का एक द्विविम चित्र में आरेखण करते हैं तथा प्रत्येक असमिका का हल क्षेत्र निर्धारित करते हैं।इसके पश्चात सभी प्रतिबन्धों की असमिकाओं का उभयनिष्ठ हल क्षेत्र OABC (छायांकित) समस्या का सुसंगत हल क्षेत्र प्राप्त होता हैं।बहुभुज के किसी एक शीर्ष पर इष्टतम हल प्राप्त होता है।
अब बहुभुज OABC क्षेत्र के शीर्षों के निर्देशांक निम्न हैं:
O(0,0) A(\frac{7}{2},0) ,B(\frac{112}{59},\frac{135}{59}),C(0,3)
उपर्युक्त शीर्षों पर उद्देश्य फलन Z में निर्देशांक प्रतिस्थापित कर इष्टतम हल की परिकलना निम्न है:
| शीर्ष | निर्देशांक | उद्देश्य फलन Z का मान |
| z=5 x_{1}+7 x_{2} | ||
| O | (0,0) | 5 \times 0+7 \times 0=0 |
| A | (\frac{7}{2},0) | 5 \times \frac{7}{2}+7 \times 0=\frac{35}{2} |
| B | (\frac{112}{59},\frac{135}{59}) | 5 \times \frac{112}{59}+7 \times \frac{125}{59}=\frac{1505}{59} |
| C | (0,3) | 5 \times 0+7 \times 3=21 |
उपर्युक्त तालिका से स्पष्ट है कि उद्देश्य फलन Z का इष्टतम मान (\frac{112}{59},\frac{135}{59}) पर प्राप्त होता है।अत: समस्या का इष्टतम हल है: x_{1}=\frac{112}{59}=1.9,x_{2}=\frac{135}{59}=2.29
तथा Max. Z=5 \times \frac{112}{59}+7 \times \frac{135}{59}=\frac{1505}{59}=25.51
Example:4.निम्नतम (Min.)z=x_{1}+2 x_{2}
प्रतिबन्ध (s.t.)
4 x_{1}+6 x_{2} \geq 2400 \\ x_{1}+x_{2} \geq 5000 \\ 8 x_{1}+2 x_{2} \geq 16000
तथा (and) x_{1} , x_{2} \geq 0
Solution:प्रतिबन्ध रेखाओं के संगत सरल रेखाएं निम्न हैं:
4 x_{1}+6 x_{2}=2400 \Rightarrow \frac{x_{1}}{600}+\frac{x_{2}}{400}=1 \\ x_{1}+x_{2}=5000 \Rightarrow \frac{x_{1}}{5600}+\frac{x_{2}}{5000}=1 \\ 8 x_{1}+2 x_{2}=16000 \Rightarrow \frac{x_{1}}{2000}+\frac{x_{2}}{8000}=1 \\ \frac{x_{1}}{600}+\frac{x_{2}}{400}=1 \\ \text { When } x_{1}=0 \text { then } x_{2}=400 \\ \text { when } x_{2}=0 \text { then } x_{1}=600 \\ (0,400),(600,0) \\ \frac{x_{1}}{5000}+\frac{x_{2}}{5000}=1 \\ \text { When }x=0 \text { then } x_{2}=5000 \\ \text { when } x_{2}=0 \text { then } x_{1}=5000 \\ (0,5000),(5000,0) \\ \\ \frac{-x_{1}}{2000}+\frac{x_{2}}{8000}=1 \\ \text { when } x_{1}=0 \text { then } x_{2}=8000 \\ \text { When } x_{2}=0 \text { then } x_{1}=2000\\ (0,8000),(2000,0) \\ 4 x_{1}+6 x_{2}=2400 तथा x_{1}+x_{2}=5000 का प्रतिच्छेद बिन्दु (13800,-8800)
x_{1}+x_{2}=5000 तथा 8 x_{1}+2 x_{2}=16000 का प्रतिच्छेद बिन्दु (1000,4000)
तथा का प्रतिच्छेद बिन्दु (2280,-1120)
उपर्युक्त सरल रेखाओं का एक द्विविम चित्र में आरेखण करते हैं तथा प्रत्येक असमिका का हल क्षेत्र निर्धारित करते हैं।इसके पश्चात सभी प्रतिबन्धों की असमिकाओं का उभयनिष्ठ हल क्षेत्र ABC (छायांकित) समस्या का सुसंगत हल क्षेत्र प्राप्त होता हैं।बहुभुज के किसी एक शीर्ष पर इष्टतम हल प्राप्त होता है।
अब बहुभुज ABC क्षेत्र के शीर्षों के निर्देशांक निम्न हैं:
उपर्युक्त शीर्षों पर उद्देश्य फलन Z में निर्देशांक प्रतिस्थापित कर इष्टतम हल की परिकलना निम्न है:
A(5000,0),B (1000,4000),C (0,8000)
| शीर्ष | निर्देशांक | उद्देश्य फलन Z का मान |
| z=x_{1}+2 x_{2} | ||
| A | (5000,0) | 5000+2(0)=5000 |
| B | (1000,4000) | 1000+2(4000)=9000 |
| C | (0,8000) | 0+2(8000)=16000 |
उपर्युक्त तालिका से स्पष्ट है कि उद्देश्य फलन Z का इष्टतम मान A पर प्राप्त होता हैअर्थात् न्यूनतम मान शीर्ष A(5000,0) पर प्राप्त होता है।अत: समस्या का इष्टतम हल है:
x_{1}=5000,x_{2}=0 तथा Max. Z=5000
Example:5.निम्नतम (Min.)z=2 x_{1}+3 x_{2}
प्रतिबन्ध (s.t.)
x_{1}+x_{2} \leq 4 \\ 6 x_{1}+2 x_{2} \geq 8 \\ x_{1}+5 x_{2} \geq 4 \\ x_{1} \leq 3, x_{2} \leq 3
तथा (and) x_{1} \geq 0, x_{2} \geq 0
Solution:प्रतिबन्ध रेखाओं के संगत सरल रेखाएं निम्न हैं:
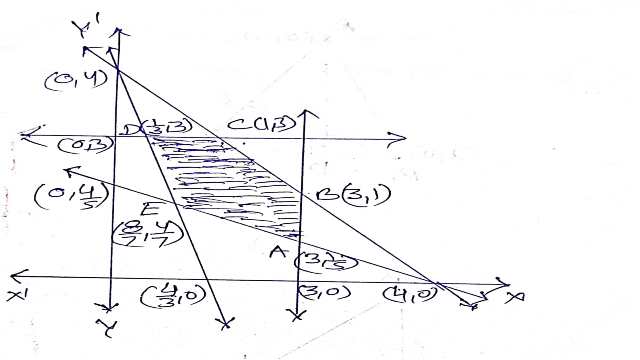
x_{1}+x_{2}=4 \Rightarrow \frac{x_{1}}{4}+\frac{x_{2}}{4}=1 \\ 6 x_{1}+2 x_{2}=8 \Rightarrow \frac{x_{1}}{\frac{4}{3}}+\frac{x_{2}}{4}=1 \\ x_{1}+5 x_{2}=4 \Rightarrow \frac{x_{1}}{4}+\frac{x_{2}}{\frac{4}{5}}=1 \\ x_{1}=3, x_{2}=3 \\ \frac{x_{1}}{4}+\frac{x_{2}}{4}=1 \\ \text { When } x_{1}=0 \text { then } x_{2}=4 \\ \text { when } x_{2}=0 \text { then } x_{1}=4 \\ (0,4),(4,0) \\ \frac{x_{1}}{\frac{4}{3}}+\frac{x_{2}}{4}=1 \\ \text { when } x_{1}=0 \text { then } x_{2}=4 \\ \text { when } x_{2}=0 \text { then } x_{1}=\frac{4}{3} \\ (0,4),\left(\frac{4}{3}, 0\right) \\ \frac{x_{1}}{4}+\frac{x_{2}}{\frac{4}{5}}=1 \\ \text { when } x_{1}=0 \text { then } x_{2}=\frac{4}{5} \\ \text { when } x_{2}=0 \text { then } x_{1}=4 \\ \left(0, \frac{4}{5}\right),(4,0) \\ x_{1}=3 तथा x_{1}+5 x_{2}=4 का प्रतिच्छेद बिन्दु
A(3,\frac{1}{5}) \\ 6 x_{1}+2 x_{2}=8 तथा x_{1}+5 x_{2}=4 का प्रतिच्छेद बिन्दु
E(\frac{8}{7},\frac{4}{7}) \\ x_{1}=3 तथा x_{1}+x_{2}=4 का प्रतिच्छेद बिन्दु B(3,1)
x_{2}=3 तथा x_{1}+x_{2}=4 का प्रतिच्छेद बिन्दु C(1,3)
x_{2}=3 तथा 6x_{1}+2x_{2}=8 का प्रतिच्छेद बिन्दु D(\frac{1}{3},3)
उपर्युक्त सरल रेखाओं का एक द्विविम चित्र में आरेखण करते हैं तथा प्रत्येक असमिका का हल क्षेत्र निर्धारित करते हैं।इसके पश्चात सभी प्रतिबन्धों की असमिकाओं का उभयनिष्ठ हल क्षेत्र ABCDE (छायांकित) समस्या का सुसंगत हल क्षेत्र प्राप्त होता हैं।बहुभुज के किसी एक शीर्ष पर इष्टतम हल प्राप्त होता है।
अब बहुभुज ABCDE क्षेत्र के शीर्षों के निर्देशांक निम्न हैं:
A(3,\frac{1}{5}),B(3,1),C(1,3),D(\frac{1}{3},3),E(\frac{8}{7},\frac{4}{7})
उपर्युक्त शीर्षों पर उद्देश्य फलन Z में निर्देशांक प्रतिस्थापित कर इष्टतम हल की परिकलना निम्न है:
| शीर्ष | निर्देशांक | उद्देश्य फलन Z का मान |
| z=2 x_{1}+3 x_{2} | ||
| A | (3,\frac{1}{5}) | 2 \times 3+3 \times \frac{1}{5}=6.6 |
| B | (3,1) | 2 \times 3+3 \times 1=9 |
| C | (1,3) | 2 \times 1+3 \times 3=11 |
| D | (\frac{1}{3},3) | 2 \times \frac{1}{3}+3 \times 3=\frac{29}{3} |
| E | (\frac{8}{7},\frac{4}{7}) | 2 \times \frac{8}{7}+3 \times \frac{4}{7}=4 |
उपर्युक्त तालिका से स्पष्ट है कि उद्देश्य फलन Z का इष्टतम हल मान E(\frac{8}{7},\frac{4}{7}) पर प्राप्त होता है।अत: समस्या का इष्टतम हल है:
x_{1}=\frac{8}{7},x_{2}=\frac{4}{7} तथा Max. Z=4
उपर्युक्त उदाहरणों के द्वारा एलपीपी संरूपण तथा आलेखी हल (LPP Formulation and Graphical Solution),रैखिक प्रोग्रामन संरूपण तथा आलेखी विधि (Linear Programming Formulation and Graphical Method) को समझ सकते हैं।
3.एलपीपी संरूपण तथा आलेखी हल की समस्याएं (LPP Formulation and Graphical Solution Problems):
आलेख विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए:
(Solve the Following L.P.P. Graphically):
(1.)अधिकतम (Max.) Z=3 x_{1}+4 x_{2}
Subject to 5 x_{1}+4 x_{2} \leq 200 \\ 3 x_{1}+5 x_{2} \leq 150 \\ 5 x_{1}+4 x_{2} \geq 100 \\ 8 x_{1}+4 x_{2} \geq 80
(and) x_{1} \geq 0, x_{2} \geq 0
(2.)अधिकतम (Max.) z=x_{1}+2 x_{2}
प्रतिबन्ध (s.t.) x_{1} \leq 80 \\ x_{2} \leq 60 \\ 5 x_{1}+6 x_{2} \leq 600 \\ x_{1}+2 x_{2} \leq 160
तथा (and) x_{1} x_{2} \geq 0
(3.)इष्टतम कीजिए (Optimize) Z=5x+3y
प्रतिबन्ध (s.t.) x+y \leq 6 \\ x \geq 3 \\ y \geq 3 \\ 2 x+3 y \geq 3
तथा (and) x \geq 0, y \geq 0
(4.)Min. Z=2x_{1}-10 x_{2}
प्रतिबन्ध (s.t.) x_{1}-x_{2} \geq 0 \\ x_{1}-5 x_{2} \leq -5
तथा (and) x_{1}, x_{2} \geq 0
उत्तर (Answers):(1)x_{1}=30.7,x_{2}=11.5 तथा अधिकतम (Max.) Z=138.1
(2.)अपरिमित इष्टतम हल
(3.)x=3,y=3,Z=24
(4.)x_{1}=\frac{5}{4},x_{2}=\frac{5}{4} तथा निम्नतम (Min.) Z=-10
उपर्युक्त सवालों को हल करने पर एलपीपी संरूपण तथा आलेखी हल (LPP Formulation and Graphical Solution),रैखिक प्रोग्रामन संरूपण तथा आलेखी विधि (Linear Programming Formulation and Graphical Method) को ठीक से समझा जा सकता है।
4.मुख्य बातें (HIGHLIGHTS):
(1.)यदि उद्देश्य फलन लाभ फलन है तो इस इष्टतम शब्द का अर्थ अधिकतम से है और उद्देश्य फलन लागत फलन है तो इष्टतम का अर्थ निम्नतम से है।
(2.)प्रत्येक प्रतिबंध या व्यवरोध में में से एक और केवल एक ही चिन्ह काम में लिया जाता है परंतु प्रत्येक व्यवरोध \leq ,=,\geq में इसका समान होना आवश्यक नहीं है।
(3.)सुसंगत हल (Feasible Solution):कुछ रैखिक प्रोग्रामन समस्या के चरों के मानों का एक ऐसा समुच्चय जो कि समस्या के सभी प्रतिबंधों (व्यवरोधों) को संतुष्ट करता हो वह समस्या का सुसंगत हल (F.S.) कहलाता है।
(4.)इष्टतम हल (Optimal Solution):किसी रैखिक प्रोग्रामन समस्या के ऐसे सुसंगत हल को इष्टतम हल कहते हैं जिसके लिए समस्या के उद्देश्य फलन का मान अधिकतम अथवा निम्नतम प्राप्त होता है।
(5.)रैखिक प्रोग्रामन समस्या को हल करने के लिए सर्वप्रथम यह विचार करना चाहिए कि दी हुई समस्या का उद्देश्य फलन एवं इसके प्रतिबन्ध(व्यवरोध) एक घातीय फलनों में व्यक्त किए जा सकते हैं या नहीं अर्थात् इसको रैखिक प्रोग्रामन विधि से हल किया जा सकता है या नहीं। इसके पश्चात उपर्युक्त विधि के अनुसार गणितीय स्वरूप में व्यक्त करना चाहिए।
Also Read This Article:-Equation of Sphere Through Circle
5.एलपीपी संरूपण तथा आलेखी हल (LPP Formulation and Graphical Solution),रैखिक प्रोग्रामन संरूपण तथा आलेखी विधि (Linear Programming Formulation and Graphical Method) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.एक रैखिक सूत्रीकरण क्या है? (What is a linear formulation?):
उत्तर:रैखिक प्रोग्रामिंग (linear programming),गणितीय मॉडलिंग तकनीक (mathematical modeling technique) जिसमें विभिन्न प्रतिबन्धों (various constraints) के अधीन होने पर एक रैखिक फलन को अधिकतम या न्यूनतम किया जाता है।यह तकनीक व्यवसाय नियोजन (business planning) में,औद्योगिक इंजीनियरिंग (industrial engineering) में और कुछ हद तक-सामाजिक और भौतिक विज्ञान (social and physical sciences) में मात्रात्मक निर्णय (quantitative decisions) लेने के लिए उपयोगी रही है।
प्रश्न:2.रैखिक प्रोग्रामिंग ग्राफिकल विधि क्या है? (What is linear programming graphical method?):
उत्तर:रेखीय प्रोग्रामिंग की ग्राफिकल विधि का उपयोग ग्राफ़ पर ऑब्जेक्टिव फंक्शन लाइन (objective function line) और सुसंगत क्षेत्र (feasible region) के बीच के उच्चतम या निम्नतम बिंदु प्रतिच्छेदन को खोजने के द्वारा समस्याओं को हल करने के लिए किया जाता है।
प्रश्न:3.रैखिक प्रोग्रामिंग मॉडल का सूत्रीकरण क्या है? (What is formulation of linear programming model?):
उत्तर:एक रैखिक प्रोग्रामिंग समस्या तैयार करने की प्रक्रिया
निर्णय चर (decision variables) की पहचान करें।उद्देश्य फलन लिखें।प्रतिबन्धों (constraints) का उल्लेख कीजिए।ऋणेत्तर प्रतिबंध (non-negativity restriction) को स्पष्ट रूप से बताएं।
प्रश्न:4.रैखिक प्रोग्रामिंग को हल करने के तरीके क्या हैं? (What are the methods of solving linear programming?):
उत्तर:चित्रमय विधि (Graphical Method)
चरण 1: एलपी (रैखिक प्रोग्रामिंग) समस्या तैयार करें [Formulate the LP (Linear programming) problem]।
चरण 2: एक ग्राफ बनाएं और प्रतिबन्ध रेखाएं बनाएं (Determine the valid side of each constraint line)।
चरण 3: प्रत्येक प्रतिबन्ध रेखा का वैध पक्ष निर्धारित करें (Determine the valid side of each constraint line)।
चरण 4: सुसंगत समाधान क्षेत्र की पहचान करें (Identify the feasible solution region)।
चरण 5: ऑब्जेक्टिव फंक्शन को ग्राफ पर प्लॉट करें (Plot the objective function on the graph)।
चरण 6: इष्टतम बिंदु खोजें (Find the optimum point)।
प्रश्न:5.एक रैखिक प्रोग्रामन के तीन घटक क्या हैं? (What are the three components of a linear program?):
उत्तर:व्याख्या: प्रतिबंधित इष्टतम मॉडल (Constrained optimization models) में तीन प्रमुख घटक होते हैं: निर्णय चर (decision variables),उद्देश्य फलन (objective function) और प्रतिबन्ध (constraints)।
प्रश्न:6.इसे रैखिक प्रोग्रामिंग क्यों कहा जाता है? (Why is it called linear programming?):
उत्तर:गणित के उन क्षेत्रों में से एक जिसका कॉम्बिनेटरियल ऑप्टिमाइजेशन (combinatorial optimization) में व्यापक उपयोग होता है,लीनियर प्रोग्रामिंग (LP) कहलाता है।इसका नाम इस तथ्य से मिलता है कि एलपी समस्या एक इष्टतमीकरण समस्या (optimization problem) है जिसमें उद्देश्य फलन (objective function) और सभी प्रतिबन्ध (constraints) रैखिक होती हैं।
प्रश्न:7.ग्राफिकल विधि के लाभ क्या हैं? (What are Advantages of Graphical Methods of Estimation?):
उत्तर:अनुमान के ग्राफिकल तरीकों के लाभ:
ग्राफिकल तरीके त्वरित और उपयोग में आसान हैं और दृश्य समझ (visual sense) में आते हैं।
गणना बहुत कम या बिना किसी विशेष सॉफ्टवेयर के की जा सकती है।
मॉडल का दृश्य परीक्षण (Visual test of model) (अर्थात बिन्दु (points) कितनी अच्छी तरह संरेखित होते हैं) यह.एक अतिरिक्त लाभ है।
प्रश्न:8.आप रैखिक प्रोग्रामिंग की ग्राफिकल विधि का उपयोग कब कर सकते हैं? (When can you use graphical method of linear programming?):
उत्तर:एलपी समस्याओं के लिए जिनमें केवल दो चर हैं,यह संभव है कि सर्वोत्तम (इष्टतम(optimal)) समाधान का पता लगाने के लिए ग्राफ पेपर पर रैखिक प्रतिबन्धों (linear constraints) को प्लॉट करके सुसंगत समाधानों (feasible solutions) के पूरे सेट को ग्राफिक रूप से प्रदर्शित किया जा सकता है।
प्रश्न:9.लीनियर प्रोग्रामिंग कितने प्रकार की होती है? (How many types of linear programming are?):
उत्तर:रैखिक प्रोग्रामिंग के विभिन्न प्रकार हैं:
सिंप्लेक्स विधि द्वारा रैखिक प्रोग्रामिंग को हल करना (Solving linear programming by Simplex method)।
R का उपयोग करके रैखिक प्रोग्रामिंग को हल करना (Solving linear programming using R)।
ग्राफिकल विधि द्वारा रैखिक प्रोग्रामिंग को हल करना (Solving linear programming by graphical method)।
ओपन सॉल्वर के उपयोग से रैखिक प्रोग्रामिंग को हल करना (Solving linear programming with the use of an open solver)।
प्रश्न:10.रैखिक प्रोग्रामिंग के अनुप्रयोग क्या हैं? (What are the applications of linear programming?):
उत्तर:रैखिक प्रोग्रामिंग के लिए अनुप्रयोग के कुछ क्षेत्रों में खाद्य और कृषि (food and agriculture),इंजीनियरिंग (engineering),परिवहन (transportation),विनिर्माण और ऊर्जा (manufacturing and energy) शामिल हैं।
रैखिक प्रोग्रामिंग अवलोकन (Linear Programming Overview)।
खाद्य और कृषि (Food and Agriculture)।
इंजीनियरिंग में अनुप्रयोग (Applications in Engineering)।
परिवहन इष्टतमीकरण (Transportation Optimization)।
कुशल विनिर्माण (Efficient Manufacturing)।
ऊर्जा उद्योग (Energy Industry)।
प्रश्न:11.रैखिक प्रोग्रामिंग की मूल अवधारणाएं क्या हैं? (What are the basic concepts of linear programming?):
उत्तर:एक रैखिक प्रोग्राम में चर का एक सेट होता है,एक रैखिक उद्देश्य फ़ंक्शन होता (linear objective function) है जो वांछित परिणाम में प्रत्येक चर के योगदान को दर्शाता है और चर के मूल्यों पर सीमाओं का वर्णन करने वाले रैखिक प्रतिबन्धों (linear constraints) का एक सेट होता है।
प्रश्न:12.रैखिक प्रोग्रामिंग समस्या की विशेषताएं क्या हैं? (What are the characteristics of linear programing problem?):
उत्तर:रैखिक प्रोग्रामिंग की विशेषताएं हैं:उद्देश्य फलन (objective function),प्रतिबन्ध (constraints),गैर-नकारात्मकता (non-negativity),रैखिकता (linearity) और परिमितता (finiteness)।
प्रश्न:13.रैखिक प्रोग्रामिंग के जनक कौन थे? (Who was the father of linear programming?):
उत्तर:डेंट्ज़िग (Dantzig)
उनके एल्गोरिथ्म को सिंप्लेक्स विधि (simplex method) कहा जाता है।Dantzig को दुनिया भर में रैखिक प्रोग्रामिंग के जनक के रूप में जाना जाता है।उन्हें अपने जीवन में अनगिनत सम्मान और पुरस्कार मिले,जिसमें राष्ट्रीय विज्ञान पदक (National Medal of Science) भी शामिल है।लेकिन उन्हें नोबेल पुरस्कार समिति द्वारा पारित कर दिया गया था,भले ही रैखिक प्रोग्रामिंग नहीं थी।
प्रश्न:14.एलपीपी में ग्राफिकल विधि की सीमा क्या है? (What is the limitation of graphical method in LPP?):
उत्तर:ग्राफिकल पद्धति की एक और सीमा यह है कि,एक गलत (incorrect) या असंगत ग्राफ (inconsistent graph) गलत उत्तर देगा,इसलिए ग्राफ को खींचते और प्लॉट करते समय बहुत सावधानी बरतने की जरूरत है।किसी भी माप (size) की रैखिक प्रोग्रामिंग समस्याओं को हल करने का एक बहुत ही उपयोगी तरीका तथाकथित सिम्प्लेक्स विधि (Simplex method) है।
प्रश्न:15.नॉनलाइनियर प्रोग्रामिंग के प्रकार क्या हैं? (What are the types of nonlinear programming?):
उत्तर:यदि आपके पास MATLAB है,तो नॉनलाइनियर ऑप्टिमाइज़ेशन (nonlinear optimization) के लिए कई विकल्प हैं: MATLAB ऑप्टिमाइज़ेशन टूलबॉक्स में अप्रतिबंधित (unconstrained) और प्रतिबन्धित (constrained) नॉनलाइनियर ऑप्टिमाइज़ेशन के लिए सॉल्वर,कम से कम-स्क्वायर ऑप्टिमाइज़ेशन (least-squares optimization),साथ ही रैखिक और द्विघात प्रोग्रामिंग के लिए एल्गोरिदम शामिल हैं।
प्रश्न:16.रैखिक प्रोग्रामिंग की खोज किसने की? (Who discovered the linear programming?):
उत्तर:जॉर्ज बी. डेंटज़िगो (George B. Dantzig)
जॉर्ज बी.डेंट्ज़िग,गणितज्ञ,जिन्होंने रैखिक प्रोग्रामिंग के क्षेत्र का आविष्कार किया,जिसने सरकारी और निजी उद्यमों की योजना बनाई,अनुसूचित और आम तौर पर अपने व्यवसाय का संचालन करने के तरीके में क्रांति ला दी,की मृत्यु हो गई है।वह 90 वर्ष के थे।
उपर्युक्त प्रश्नों के उत्तर द्वारा एलपीपी संरूपण तथा आलेखी हल (LPP Formulation and Graphical Solution),रैखिक प्रोग्रामन संरूपण तथा आलेखी विधि (Linear Programming Formulation and Graphical Method) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
LPP Formulation and Graphical Solution
एलपीपी संरूपण तथा आलेखी हल
(LPP Formulation and Graphical Solution)
LPP Formulation and Graphical Solution
एलपीपी संरूपण तथा आलेखी हल (LPP Formulation and Graphical Solution):
प्रत्येक व्यक्ति के लिए निर्णयन (Decision Making) एक बहुत महत्वपूर्ण
परिघटना (Phenomenon) है।
- 1.एलपीपी संरूपण तथा आलेखी हल (LPP Formulation and Graphical Solution),रैखिक प्रोग्रामन संरूपण तथा आलेखी विधि (Linear Programming Formulation and Graphical Method):