LPP Formulation and Graphical Method
1.रैखिक प्रोग्रामन समस्या संरूपण तथा आलेखी विधि (LPP Formulation and Graphical Method),रैखिक प्रोग्रामन संरूपण तथा आलेखी हल (Linear Programming Formulation and Graphical Solution):
रैखिक प्रोग्रामन समस्या संरूपण तथा आलेखी विधि (LPP Formulation and Graphical Method):सन् 1947 में जार्ज बी डेन्टजिग, मार्शल वुड तथा उसके साथी जो कि संयुक्त राज्य अमेरिका की वायुसेना के अधिकारी थे, सर्वप्रथम रैखिक प्रोग्रामन का संरूपण तथा इसके हल करने का नियमित कार्य विधि,मारक शक्तियों का अनुकूलतम प्रकार से नियोजन करने के लिए किया था।
चूंकि प्रारंभ में इसका प्रयोग केवल युद्ध में होता था इसलिए इसको प्रारंभ में संक्रिया विज्ञान (Operation Research) कहा जाता था परंतु वर्तमान युग में संक्रिया विज्ञान के स्थान पर प्रायः रैखिक प्रोग्रामन का प्रयोग किया जाता है।रैखिक प्रोग्रामन सर्व उत्तम हल ज्ञात करने की एक विशेष प्रकार की बहुत ही उत्तम तकनीक (Technology) है।
रैखिक असमिकाओं का आलेखी निरूपण (Graphical Represention of Linear Inequalities):
दो चरों की एक घातीय असमिका सदैव एक तल के दो भागों में से एक भाग (Portion) को प्रदर्शित करती है।प्रत्येक रैखिक असमिका का लेखाचित्र आरेखन के लिए पहले उसके संगत समीकरण लिखते हैं तथा उसको द्विविम (Two Dimensional) समतल में आलेखित करते हैं जो कि संगत असमिका को प्रदर्शित करते हैं जिसे संगत सरल रेखा पर तीर द्वारा प्रदर्शित करते हैं।इस क्षेत्र को उस असमिका (Inequality) का हल क्षेत्र (Solution Space) कहते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-LPP Formulation and Graphical Solution
2.रैखिक प्रोग्रामन समस्या संरूपण तथा आलेखी विधि के उदाहरण (LPP Formulation and Graphical Method):
प्रश्न:1.एक लघु निर्माता 5 कुशल तथा 10 अर्द्धकुशल कारीगरों को लगाकर एक वस्तु मॉडल डीलक्स एवं साधारण बनाता है।एक डीलक्स मॉडल बनाने में एक कुशल कारीगर के 2 घंटे तथा अर्द्धकुशल कारीगर के भी 2 घण्टे लगते हैं।एक साधारण मॉडल बनाने में एक कुशल कारीगर का एक घंटा तथा अर्द्धकुशल कारीगर के 3 घंटे लगते हैं।श्रमिक संगठन के नियमानुसार कोई भी कारीगर 8 घंटे प्रतिदिन से अधिक कार्य नहीं कर सकता है। निर्माता का शुद्ध लाभ प्रत्येक डीलक्स मॉडल पर ₹10 एवं प्रत्येक साधारण मॉडल पर ₹8 हो तो लेखाचित्र विधि से ज्ञात कीजिए कि अधिकतम दैनिक लाभ कमाने के लिए उसे प्रत्येक प्रकार की कितनी वस्तुएं बनानी चाहिए?
(A small manufacturer has employed 5 skilled men and 10 semiskilled men and makes an article in two qualities delux model and an ordinary model.The making of a delux model requires 2 hours work by a skilled man and 2 hours work by a semi-skilled men.The ordinary model requires one hour by a skilled man and 3 hours work by a semi-skilled man.By union rules no man more than 8 hours per day.The manufacturer’s clear profit on a delux model is ₹10 and an ordinary model in ₹80.Then find by graphical method that how many of each type should be made in order to maximize his total daily profit.)
Solution:गणितीय संरूपण (Mathematical Formulation of the Problem):
| कारीगर | डीलक्स माॅडल x_{1} | साधारण माॅडल x_{2} | एक दिन में उपलब्ध कुल घण्टे उपलब्ध (क्षमता) |
| कुशल कारीगर | 2 | 1 | 40 |
| अर्द्धकुशल कारीगर | 2 | 3 | 80 |
| लाभ रु. में | 10 | 8 |
माना कि कारीगर एक दिन में डीलक्स माॅडल तथा साधारण माॅडल वस्तु बनाने पर अधिकतम लाभ Z होता है।
अब डीलक्स माॅडल को कुशल कारीगर 2 घण्टे और साधारण माॅडल को बनाने के लिए 1 घण्टा लेता है।अतः प्रश्नानुसार:
2 x_{1}+x_{2} \leq 40
इसी प्रकार अर्द्धकुशल कारीगर के लिए:
2 x_{1}+3 x_{2} \leq 80
कुल लाभ x_{1} डीलक्स माॅडल और x_{2} साधारण माॅडल के लिए: 10 x_{1}+8 x_{2}
अतः दी हुई समस्या का गणितीय स्वरूप निम्न प्रकार होगा:
अधिकतम (Max.)z=10 x_{1}+8 x_{2}
प्रतिबन्ध (s.t.) 2 x_{1}+x_{2} \leq 40,2 x_{1}+3 x_{2} \leq 80, x_{1}, x_{2} \geq 0
आलेखी हल:प्रतिबन्ध अमिकाओं के संगत सरल रेखाएं निम्न है:
2 x_{1}+x_{2}=40 \Rightarrow \frac{x_{1}}{20}+\frac{x_{2}}{40}=1 \\ 2 x_{2}+3 x_{2}=80 \Rightarrow \frac{x_{1}}{40}+\frac{x_{2}}{\frac{80}{3}}=1 \\ x_{1}=0, x_{2}=0 \\ \frac{x_{1}}{20}+\frac{x_{2}}{40}=1
जब x_{1}=0 तो x_{2}=40
जब x_{2}=0 तो x_{1}=20
(0,40),(20,0) \\ \frac{x_{1}}{40}+\frac{x_{2}}{\frac{80}{3}}=1
जब x_{1}=0 तो x_{2}=\frac{80}{3}
जब x_{2}=0 तो x_{1}=40
(0,\frac{80}{3}),(40,0)
सरल रेखाओं का प्रतिच्छेद बिन्दु:
2 x_{1}+x_{2}=40 \cdots(1) \\ 2 x_{1}+3 x_{2}=80 \cdots(2)
उपर्युक्त सरल रेखाओं का एक द्विविम चित्र में आरेखन करते हैं तथा प्रत्येक असमिका का हल क्षेत्र निर्धारित करते हैं।
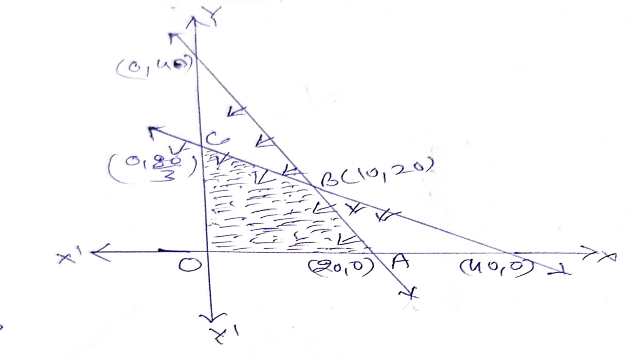
इसके पश्चात् सभी प्रतिबन्धो की असमिकाओं के क्षेत्रों का उभयनिष्ठ हल क्षेत्र OABC (छायांकित) समस्या का सुसंगत हल क्षेत्र प्राप्त होता है।आलेख से बहुभुज के शीर्षों के निर्देशांक निम्न हैं:
O(0,0),A(20,0),B(10,20),C(0,\frac{80}{3})
उपर्युक्त शीर्षों पर उद्देश्य फलन में निर्देशांक प्रतिस्थापित कर इष्टतम हल की परिकलना निम्न प्रकार है:
| शीर्ष | निर्देशांक | उद्देश्य फलन Z का मान |
| Z=10x_{1}+8x_{2} | ||
| O | (0,0) | 10(0)+8(0)=0 |
| A | (20,0) | 10(20)+8(0)=200 |
| B | (10,20) | 10(10)+8(20)=260 |
| C | (0,\frac{80}{3}) | 10(0)+8(\frac{80}{3})=(\frac{640}{3}) |
उपर्युक्त तालिका से स्पष्ट है कि उद्देश्य फलन Z का अधिकतम मान शीर्ष B(10,20) पर प्राप्त होता है।
अतः समस्या का इष्टतम हल निम्न है: x_{1}=10, x_{2}=20
तथा अधिकतम (Max.)Z=260
Example:2.F_{1} और F_{2} दो तरह के खाद्य पदार्थ हैं तथा इनमें विटामिन V_{1},V_{2} और V_{3} हैं।एक मानव शरीर की रोजाना की कम से कम जरूरत है।एक मिग्रा V_{1} की ,50 मिग्रा V_{2}और 10 मिग्रा V_{3} की है।यह मालूम है कि खाद्य पदार्थ F_{1} में 1 मिग्रा V_{1} की,100 मिग्रा V_{2} की और 100 मिग्रा V_{3} की मात्रा है एवं खाद्य पदार्थ F_{2} में एक मिग्रा V_{1} की,10मिग्रा V_{2} की और 100 मिग्रा V_{3} की मात्रा है।खाद्य पदार्थ F_{1} की एक इकाई का मूल्य एक रुपया है और F_{2} का 1.50 रुपए हैं।उस आहार का न्यूनतम मूल्य ज्ञात कीजिए जिससे शरीर को प्रत्येक विटामिन की कम से कम न्यूनतम मात्रा मिल सके।
(There are two different types of foodstuffs F_{1} and F_{2} these contain vitamins V_{1},V_{2}and V_{3} respectively.Minimum daily requirement of these vitamins for a human body are 1mg of V_{1} ;50 mg of V_{2} and 10mg of V_{3}. It is known that foodstuff F_{1} contains 1 mg of V_{1}, 100 mg of V_{2}, 10 mg of V_{3}; whereas foodstuff F_{2} contains 1mg of V_{1},10mg of V_{2} and 100mg of V_{3},cost of one unit of foodstuff F_{1} Rs.1 and that of F_{2} is Rs.1.50.Find the minimum cost diet that would supply the body at least the minimum (requirements of each vitamin.)
Solution:गणितीय संरूपण (Mathematical Formulation of the Problem)
| विटामिन | खाद्य पदार्थF_{1} | खाद्य पदार्थF_{2} | मानव शरीर को रोजाना विटामिन की जरुरत |
| V_{1} | 1 | 1 | 1 |
| V_{2} | 100 | 10 | 50 |
| V_{3} | 10 | 100 | 10 |
| मूल्य | 1 | 1.5 |
माना कि मानव शरीर की खाद्य पदार्थ F_{1} की x_{1} तथा खाद्य पदार्थ F_{2} की x_{2}आहार पर न्यूनतम मूल्य Z है।
अब खाद्य पदार्थ F_{1} की मात्रा 1मिग्रा विटामिन V_{1} तथा 1मिग्रा खाद्य पदार्थ F_{2} की विटामिन V_{1} मानव शरीर को जरूरत है।
अतः प्रश्नानुसार x_{1}+x_{2} \geq 1
इसी प्रकार विटामिन V_{2} के लिए 100 x_{1}+10 x_{2} \geq 50 \\ \Rightarrow 10 x_{1}+x_{2} \geq 5
विटामिन V_{3} के लिए 10 x_{1}+100 x_{2} \geq 10 \\ \Rightarrow x_{1}+10 x_{2} \geq 1
उद्देश्य फलन Z: न्यूनतम (Min.)Z=x_{1}+1.5 x_{2}
अतः समस्या का गणितीय स्वरूप निम्न होगा: Z=x_{1}+1.5 x_{2}
प्रतिबन्ध (s.t.) x_{1}+x_{2} \geq 1 \\ 10 x_{1}+x_{2} \geq 5 , \quad x_{1}+10 x_{2} \geq 1, \quad x_{1} x_{2} \geq 0
आलेखी हल:प्रतिबन्ध की असमिकाओं के संगत सरल रेखाएं निम्न हैं:
x_{1}+x_{2}=1 \\ 10 x_{1}+x_{2}=5 \Rightarrow \frac{x_{1}}{\frac{1}{2}}+\frac{x_{2}}{5}=1 \\ x_{1}+10 x_{2}=1 \Rightarrow \frac{x_{1}}{1}+\frac{x_{2}}{\frac{1}{10}}=1 \\ \Rightarrow x_{1}=0, x_{2}=0 \\ x_{1}+x_{2}=1
जब x_{1}=0 तो x_{2}=1
जब x_{2}=0 तो x_{1}=1
(0,1),(1,0) \\ \frac{x_{1}}{\frac{1}{2}}+\frac{x_{2}}{5}=1
जब x_{1}=0 तो x_{2}=5
जब x_{2}=0 तो x_{1}=\frac{1}{2}
(0,5),(\frac{1}{2},0) \\ \frac{x_{1}}{1}+\frac{x_{2}}{\frac{1}{10}}=1
जब x_{1}=0 तो x_{2}=\frac{1}{10}
जब x_{2}=0 तो x_{1}=1
(0,\frac{1}{10}),(1,0)
सरल रेखाओं 10 x_{1}+x_{2}=5 तथा x_{1}+10 x_{2}=1 का प्रतिच्छेद बिन्दु \left(\frac{49}{99}, \frac{5}{99}\right) है।
उपर्युक्त सरल रेखाओं का एक द्विविम चित्र में आरेखन करते हैं तथा प्रत्येक असमिका का हल क्षेत्र निर्धारित करते हैं।
इसके पश्चात् सभी प्रतिबन्धो की असमिकाओं के क्षेत्रों का उभयनिष्ठ हल क्षेत्र ABC (छायांकित) समस्या का सुसंगत हल क्षेत्र प्राप्त होता है।आलेख से बहुभुज के शीर्षों के निर्देशांक निम्न हैं:
A(1,0),B(\frac{4}{9},\frac{5}{9}),C(0,5),
उपर्युक्त शीर्षों पर उद्देश्य Z फलन में निर्देशांक प्रतिस्थापित कर इष्टतम हल की परिकलना निम्न प्रकार है:
| शीर्ष | निर्देशांक | उद्देश्य फलन Z का मान z=x_{1}+1.5x_{2} |
| A | (1,0) | 1+1.5(0)=1 |
| B | (\frac{4}{9},\frac{5}{9}) | \frac{4}{9}+1.5 \times \frac{5}{9} =\frac{11.5}{9} |
| C | (0,5) | 0+1.5 \times 5=7.5 |
उपर्युक्त तालिका से स्पष्ट है कि उद्देश्य फलन Z का न्यूनतम मान शीर्ष A(1,0) पर प्राप्त होता है।
अतः समस्या का इष्टतम हल निम्न है:x_{1}=1,x_{2}=0
तथा न्यूनतम (Min.)Z=1
उपर्युक्त उदाहरणों के द्वारा रैखिक प्रोग्रामन समस्या संरूपण तथा आलेखी विधि (LPP Formulation and Graphical Method),रैखिक प्रोग्रामन संरूपण तथा आलेखी हल (Linear Programming Formulation and Graphical Solution) को समझ सकते हैं।
3.रैखिक प्रोग्रामन समस्या संरूपण तथा आलेखी विधि की समस्याएं (LPP Formulation and Graphical Method Problems):
(1.)एक स्वचालित वाहन निर्माता अपनी फैक्ट्री में जो दो कार्यशाला में विभाजित है मोटर कारें और ट्रक बनाता है।पहली कार्यशाला में जहां प्रारंभिक ढांचे तैयार किए जाते हैं,एक ट्रक के लिए 5 मानव दिवस तथा एक मोटर कार के लिए 2 मानव दिवस लगते हैं।दूसरी कार्यशाला में जिसमें वाहनों को अंतिम रूप दिया जाता है ,प्रत्येक निर्मित ट्रक या मोटर कार के लिए 3 मानव दिवस लगते हैं।मशीन एवं मानव की सीमाओं के कारण पहली कार्यशाला में 180 मानव दिवस प्रति सप्ताह तथा दूसरी कार्यशाला में 135 मानव दिवस प्रति सप्ताह उपलब्ध है।यदि निर्माता को प्रत्येक ट्रक पर ₹3000 तथा प्रत्येक मोटरकार पर ₹2000 का लाभ हो तो लेखाचित्र विधि से ज्ञात कीजिए कि निर्माता को अधिकतम लाभ हेतु प्रत्येक प्रकार के कितने वाहन बनाने चाहिए?
(An Automobile manufacturer makes moter cars and trucks in a factory that is divided into two shops.Shop I, which performs the basic assembly operation,must work 5 man days on each trucks but only 2 man-work on each cars.Shop II which performs finishing operations must work 3 man days for each motee car or truck that is produced.Because of man and machine limitation,Shop I has 180 man days per week available while shop II has 135 man days per week.If the manufacturer makes a profit of Rs.3,000 on each truck and Rs. 2000 on each moter car,find graphically how many of each should be produced to maximize his profit.)
प्रश्न:2.एक कार बनाने वाली मोटर कंपनी दो नमूनों A तथा B की कार बनाती है।ये कारें ₹2000 प्रति नमूना A तथा ₹1000 प्रति नमूना B के लाभ पर व्यापारियों को बेच दी जाती है।नमूना A के लिए 150 मानव घण्टे संयोजन के लिए,50 मानव घंटे रंग-रोगन और परिसज्जा के लिए और 10 मानव घंटे का जांचने एवं परीक्षण के लिए आवश्यकता होती है।नमूना B के लिए 60 मानव घंटे संयोजन के लिए,40 मानव बंटी रंग-रोगन और परिसज्जा के लिए,20 मानव घंटे जांचने और परीक्षण के लिए उपलब्ध है।आलेखीय विधि से समस्या को हल करते हुए यह बताइए कि अधिकतम लाभ के लिए कंपनी ने नमूने A और नमूने B की कितने कारें बनाये?
(A motor company manufactures two car models A and B.There are sold to car dealers at a profit of Rs.2000 per model A and 1,000 per model B.Model A requires 150 man-hours for assembly,50 man hours for painting and finishing and 10 man hours for checking and testing.Model B requires 60 man-hours of assembly 40 man-hours for painting and finishing and 20 man-hours for checking and testing.There are 30,000 man-hours available in the assembly shop 13,000 man-hours in the painting and finishing shop and 5,000 man hours in the checking and testing division.How many cars of model A and model B should the company produce.So as to gain maximum profit?Use graphical method to solve the problem.
उत्तर (Answers):(1.)शीर्ष B(15,30) पर अधिकतम (Max.) Z=1,20,000 (2.)शीर्ष (140,150) पर अधिकतम (Max.) Z=4,30,000
उपर्युक्त सवालों को हल करने पर रैखिक प्रोग्रामन समस्या संरूपण तथा आलेखी विधि (LPP Formulation and Graphical Method),रैखिक प्रोग्रामन संरूपण तथा आलेखी हल (Linear Programming Formulation and Graphical Solution) को ठीक से समझ सकते हैं।
Also Read This Article:-Derivative of Length of an Arc
4.मुख्य बिन्दु (HIGHLIGHTS):
क्रियाविधि (Working Producer):
(1.)रैखिक प्रोग्रामन समस्या के व्यवरोध (प्रतिबन्ध) के संगत रैखिक समीकरण लिखिए जो एक रेखा को व्यक्त करती है।
(2.)द्विविम लेखाचित्र में उपर्युक्त रेखाओं को अंकितकर
,असमिकाओं का हल चित्र अंकित कीजिए।
(3.)उपर्युक्त सभी व्यवरोध (प्रतिबन्ध),असमिकाओं के क्षेत्रों में उभयनिष्ठ क्षेत्र (सीमित अथवा असीमित) बहुभुज को छायांकित कीजिए।
(4.)बहुभुज के समस्त शीर्षों के निर्देशांक लेखाचित्र से ज्ञात करते हैं (अथवा संगत भुजाओं की समीकरणों को हल करके भी ज्ञात कर सकते हैं)।
(5.)सुसंगत हल क्षेत्र में अनंत बिंदु ऐसे हैं जो कि समस्या का हल है परंतु इष्टतम हल तो केवल बहुभुज के शीर्ष बिन्दु पर ही विद्यमान हैं इसलिए बहुभुज के शीर्ष बिन्दु के निर्देशांक को उद्देश्य फलन में बारी-बारी से प्रतिस्थापित कर इष्टतम हल उनमें से ज्ञात करते हैं।
(6.)यदि शीर्ष बिंदु इष्टतम हल ज्ञात करने में असमर्थ हो जाएं तो समस्या का हल असीमित होता है और यदि उभयनिष्ठ क्षेत्र में कोई बिंदु विद्यमान न हो तो समस्या का हल नहीं होता है।
5.रैखिक प्रोग्रामन समस्या संरूपण तथा आलेखी विधि (LPP Formulation and Graphical Method) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.सुसंगत हल को परिभाषित कीजिए। (Define feasible Solution.):
उत्तर:कुछ रैखिक प्रोग्रामन समस्या के चरों के मानों का एक ऐसा समुच्चय जो कि समस्या के सभी प्रतिबन्धों (व्यवरोधों) को सन्तुष्ट करता है वह समस्या का सुसंगत हल (F.S.) कहलाता है।
प्रश्न:2.इष्टतम हल क्या होता है? (What is optimal solution?):
उत्तर:किसी रैखिक प्रोग्रामन समस्या के ऐसे सुसंगत हल को इष्टतम हल कहते हैं जिसके लिए समस्या के उद्देश्य फलन का मान अधिकतम अथवा निम्नतम प्राप्त होता है।
प्रश्न:3.रैखिक प्रोग्रामन को परिभाषित कीजिए। (Define linear programming.):
उत्तर:रैखिक प्रोग्रामन वह तकनीक है जिसका प्रयोग उन प्रोग्रामन समस्याओं में किया जाता है जिसमें उपलब्ध सीमित साधनों का अनुकूलतम अधिकतम लाभ या निम्नतम लागत देने वाला हल ज्ञात किया जाता है।
प्रश्न:4.रैखिक प्रोग्रामन समस्या का गणितीय स्वरूप लिखिए। (Write the mathematical model of a LPP.):
उत्तर:एक n-चरों की रैखिक प्रोग्रामन समस्या का कुछ प्रतिबन्धों सहित प्रक्कथन निम्न प्रकार है:
इष्टतम करो Z=c_{1} x_{1} + c_{2} x_{2}+c_{3} x_{3}+\cdots +c_{n} x_{n}
प्रतिबन्ध (Subject to the conditions):
a_{11} x_{1}+a_{12} x_{2}+a_{13} x_{3}+\ldots+a_{1 n} x_{n} \leq \left(\text{या }=\text{ या } \geq \right) b_{1} \\ a_{21 x_{1}}+a_{22} x_{2}+a_{23} x_{3}+\cdots+a_{2 n} x_{n} \leq \left(\text{ या }=\text{ या } \geq \right) b_{2} \\ a_{31} x_{1}+a_{32} x_{2}+a_{33} x_{3} +\cdots a_{3 n} x_{n} \leq \left(\text{ या }=\text{ या } \geq \right) b_{3} \\ …… ………………………………….…….. \\ a_{m_{1}}x_{1}+a_{m 2} x_{2}+a_{m 3} x_{3}+\cdots+a_{m n} x_{n} \leq\left(\text{ या }=\text{ या } \geq \right) b_{n}
तथा ऋणेतर प्रतिबन्ध x_{j} \geq 0,j=1,2,3 \cdots n
उपर्युक्त प्रश्नों के उत्तर द्वारा रैखिक प्रोग्रामन समस्या संरूपण तथा आलेखी विधि (LPP Formulation and Graphical Method),रैखिक प्रोग्रामन संरूपण तथा आलेखी हल (Linear Programming Formulation and Graphical Solution) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
- 1.रैखिक प्रोग्रामन समस्या संरूपण तथा आलेखी विधि (LPP Formulation and Graphical Method),रैखिक प्रोग्रामन संरूपण तथा आलेखी हल (Linear Programming Formulation and Graphical Solution):
- 2.रैखिक प्रोग्रामन समस्या संरूपण तथा आलेखी विधि के उदाहरण (LPP Formulation and Graphical Method):
- 3.रैखिक प्रोग्रामन समस्या संरूपण तथा आलेखी विधि की समस्याएं (LPP Formulation and Graphical Method Problems):
- 4.मुख्य बिन्दु (HIGHLIGHTS):
- 5.रैखिक प्रोग्रामन समस्या संरूपण तथा आलेखी विधि (LPP Formulation and Graphical Method) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
- प्रश्न:1.सुसंगत हल को परिभाषित कीजिए। (Define feasible Solution.):
- प्रश्न:2.इष्टतम हल क्या होता है? (What is optimal solution?):
- प्रश्न:3.रैखिक प्रोग्रामन को परिभाषित कीजिए। (Define linear programming.):
- प्रश्न:4.रैखिक प्रोग्रामन समस्या का गणितीय स्वरूप लिखिए। (Write the mathematical model of a LPP.):
- रैखिक प्रोग्रामन समस्या संरूपण तथा आलेखी विधि (LPP Formulation and Graphical Method)
LPP Formulation and Graphical Method
रैखिक प्रोग्रामन समस्या संरूपण तथा आलेखी विधि
(LPP Formulation and Graphical Method)
LPP Formulation and Graphical Method
रैखिक प्रोग्रामन समस्या संरूपण तथा आलेखी विधि (LPP Formulation and Graphical Method):सन् 1947 में
जार्ज बी डेन्टजिग, मार्शल वुड तथा उसके साथी जो कि संयुक्त राज्य अमेरिका की वायुसेना के अधिकारी थे