How to Solve LPP by Two Phase Method?
1.एलपीपी को द्विप्रावस्था विधि द्वारा कैसे हल करें? (How to Solve LPP by Two Phase Method?),रैखिक प्रोग्रामन समस्याओं को द्विप्रावस्था विधि से हल करना (To Solve Linear Programming Problems by Two Phase Method):
एलपीपी को द्विप्रावस्था विधि द्वारा कैसे हल करें? (How to Solve LPP by Two Phase Method?) इस आर्टिकल में इसी द्विप्रावस्था विधि के द्वारा एलपीपी के सवालों को हल किया गया है।द्विप्रावस्था विधि वस्तुतः रैखिक प्रोग्रामन समस्या को हल करने की एक वैकल्पिक विधि है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-How to Solve LPP by Simplex Method?
2.एलपीपी को द्विप्रावस्था विधि द्वारा कैसे हल करें पर आधारित उदाहरण (Examples Based on How to Solve LPP by Two Phase Method?):
निम्न रैखिक प्रोग्रामन समस्याओं को द्विप्रावस्था विधि से हल करिए:
(Solve the following L.P.P. by two phase method):
Example:1.निम्नतम (Min.) Z=2 x_1+9 x_2+x_3
प्रतिबन्ध (s.t.) x_1+4 x_2+2 x_3 \geq 5 \\ 3 x_1+x_2+2 x_3 \geq 4
तथा (and) x_1, x_2, x_3 \geq 0
Solution:सर्वप्रथम उद्देश्य फलन को अधिकतमीकरण की समस्या में बदलते हैं।चूँकि यह निम्नतमीकरण की समस्या है,तत्पश्चात प्रतिबन्ध असमिकाओं में x_4 तथा x_5 आधिक्यपूरक चर घटाने पर समस्या का परिवर्तित रूप निम्न प्रकार होगा:
अधिकतम W=-2 x_1-9 x_2-x_3+0 x_4+0 x_5
प्रतिबन्ध x_1+4 x_2+2 x_3-x_4+0 x_5=5 \\ 3 x_1+x_2+2 x_3+0 x_4-x_5=4
तथा x_1, x_2, x_3, x_4, x_5 \geq 0
इस समस्या का प्रारम्भिक हल प्राप्त नहीं कर सकते।चूँकि इसके गुणांक मैट्रिक्स में एकिक उपमैट्रिक्स I_2 विद्यमान नहीं है,अतः उपर्युक्त समीकरणों में कृत्रिम चर x_6 तथा x_7 जोड़ते हैं तथा उद्देश्य फलन में इनके मूल्य -1 रखते हैं तथा कृत्रिम चरों के अतिरिक्त अन्य चरों का मूल्य शून्य रखने पर:
अधिकतम Z^{*}=0 x_1+0 x_2+0 x_3+0 x_4+0 x_5-x_6 -x_7
प्रतिबन्ध x_1+4 x_2+2 x_3-x_4+0 x_5+x_6+0 x_7=5 \\ 3 x_1+x_2+2 x_3+0 x_4-x_5+0 x_6+ x_7=4
तथा x_1, x_2, x_3, x_4, x_4, x_6, x_7 \geq 0
अब प्रतिबन्ध निकाय का गुणांक मैट्रिक्स
\left[\begin{array}{ccccccc} 1 & 4 & 2 & -1 & 0 & 1 & 0 \\ 3 & 1 & 2 & 0 & -1 & 0 & 1\end{array}\right] =\left(\alpha_1 \alpha_2 \alpha_3 \alpha_4 \alpha_5 \alpha_6 \alpha_7\right) \\ \left(\alpha_6 \alpha_7 \right)=I_2 अतः प्रथम चरण कि सारणी I का प्रारम्भिक आधार B=\left(\alpha_6 \alpha_7\right) तथा सारणी निम्न प्रकार होगी:
प्रथम प्रावस्था:सारणी I
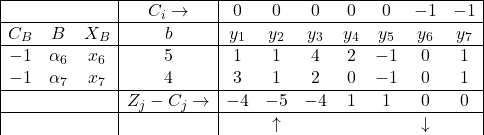
उपर्युक्त सारणी में Z_j^*-C_j के सभी मान ऋणेत्तर (Non Negative) नहीं है,अतः आधारी हल इष्टतम नहीं है।
Z_{2}^*-C_{2}=-5 निम्नतम है,अतः नये आधार के लिए प्रवेशी सदिश \alpha_{2} होगा।
पुनः \underset{i}{\text{निम्नतम}}\left\{\frac{x_{B i}}{y_{i 2}}, y_{i 2}>0\right\}=\underset{i}{\text{निम्नतम}} \left\{\frac{5}{4}, \frac{4}{1}\right\} \\ =\frac{5}{4} =\frac{x_{B1}}{y_{12}} \\ \therefore y_{12} अर्थात् 4 मुख्य अवयव तथा \alpha_{6} अपगामी सदिश होगा। \alpha_{6} चूँकि कृत्रिम चर है,अतः इसे नई सारणी में सम्मिलित नहीं करेंगे।अब सामान्य रूपान्तरणों से नवीन आधारी हल के लिए निम्न सारणी होगी:
मुख्य अवयव वाली पंक्ति (Working rule):
मुख्य अवयव वाली प्रथम पंक्ति में मुख्य अवयव 4 का भाग देने पर द्वितीय सारणी की प्रथम पंक्ति तैयार होगी:
\frac{5}{4}, \frac{1}{4}, \frac{4}{4}=1, \frac{2}{4}=\frac{1}{2}, \frac{-1}{4}, \frac{0}{4}=0, \frac{0}{4}=0
द्वितीय पंक्ति:प्रथम प्रावस्था की प्रथम सारणी की द्वितीय पंक्ति के अवयवों में से मुख्य अवयव अवयव वाली पंक्ति के अवयवों अर्थात् उपर्युक्त अवयवों को मुख्य अवयव के संगत द्वितीय पंक्ति के अवयव 1 से गुणा करके घटा देंगे:
4-\frac{5}{4} \times 1=\frac{11}{4}, 3-\frac{1}{4} \times 1=\frac{11}{4}, 1-1 \times 1=0,2-\frac{1}{2} \times 1 =\frac{3}{2} \\ 0-\left(-\frac{1}{4}\right) \times 1=\frac{1}{4},-1-(0) \times 1=-1, 1-0 \times 1=1
प्रथम प्रावस्था:सारणी II
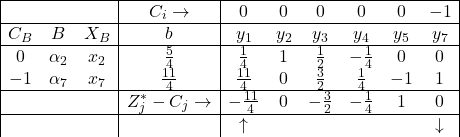
उपर्युक्त सारणी में Z_j^*-C_j के सभी मान ऋणेत्तर नहीं है।अतः आधारी हल इष्टतम हल नहीं है।नई सारणी के लिए \alpha_{1} प्रवेशी सदिश होगा,चूँकि Z_{1}^*-C_{1} का मान निम्नतम है।
पुनः \underset{i}{\text{निम्नतम}}\left\{\frac{x_{B i}}{y_{i 1}}, y_{i 1}>0\right\}=\underset{i}{\text{निम्नतम}} \left\{\frac{\frac{5}{4}}{\frac{1}{4}}, \frac{\frac{11}{4}}{\frac{11}{4}}\right\} \\ =\frac{\frac{11}{4}}{\frac{11}{4}} =\frac{x_{B2}}{y_{21}} \\ \therefore y_{21} अर्थात् \frac{11}{4} मुख्य अवयव है तथा \alpha_{7} अपगामी सदिश होगा।चूँकि \alpha_{7} एक कृत्रिम चर है,अतः नई सारणी में इसे सम्मिलित नहीं करेंगे।पुनः सामान्य रूपान्तरणों से नवीन आधारी हल के लिए निम्न सारणी होगी:
मुख्य अवयव वाली पंक्ति (Working rule):
प्रथम प्रावस्था की द्वितीय सारणी की द्वितीय पंक्ति मुख्य मुख्य अवयव वाली पंक्ति है।अतः द्वितीय पंक्ति के अवयवों में मुख्य अवयव \frac{11}{4} का भाग देने पर तृतीय सारणी की द्वितीय पंक्ति तैयार होगी:
\frac{\frac{11}{4}}{\frac{11}{4}}=1, \frac{\frac{11}{4}}{\frac{11}{4}}=1, \frac{0}{\frac{11}{4}}=0, \frac{\frac{3}{2}}{\frac{11}{4}}=\frac{6}{11}, \frac{\frac{1}{4}}{\frac{11}{4}}=\frac{1}{11}, \frac{-1}{\frac{11}{4}}=-\frac{4}{11}
प्रथम पंक्ति:प्रथम प्रावस्था की द्वितीय सारणी की प्रथम पंक्ति के अवयवों में से मुख्य अवयव वाली पंक्ति के अवयवों अर्थात् उपर्युक्त अवयवों को मुख्य अवयव के संगत प्रथम पंक्ति के अवयव \frac{1}{4} से गुणा करके घटा देंगे:
\frac{5}{4}-1 \times \frac{1}{4}=1, \frac{1}{4}-1 \times \frac{1}{4}=0,1-0 \times \frac{1}{4}=1, \frac{1}{2}-\frac{6}{11} \times \frac{1}{4}=\frac{4}{11} ,\\ -\frac{1}{4}-\frac{1}{11} \times \frac{1}{4}=-\frac{3}{11} , 0-\left(-\frac{4}{11}\right) \times \frac{1}{4}=\frac{1}{11}
प्रथम प्रावस्था:सारणी III

चूँकि Z_j^*-C_j \geq 0 तथा कोई भी कृत्रिम चर आधार में नहीं है,अतः प्रथम चरण इस स्थिति में समाप्त होता है।अतः इस सारणी से प्राप्त हल मूल समस्या का आधारी सुसंगत हल है।अब द्वितीय प्रावस्था (Phase II) में प्रवेश करते हैं।उद्देश्य फलन
W=-2 x_1-9 x_2+x_3+0 x_4+0 x_5
द्वितीय चरण:सारणी I

उपर्युक्त सारणी में Z_j-C_j के सभी मान ऋणेत्तर \geq 0 नहीं है,अतः आधारी हल इष्टतम नहीं है।नई सारणी के लिए \alpha_{3} प्रवेशी सदिश होगा।चूँकि Z_3^*-C_3 का मान निम्नतम है।
\underset{i}{\text{निम्नतम}}\left\{\frac{x_{B i}}{y_{i 3}}, y_{i 3}>0\right\}=\underset{i}{\text{निम्नतम}}\left\{\frac{1}{\frac{4}{11}}, \frac{1}{\frac{6}{11}}\right\} \\ =\frac{1}{\frac{6}{11}} =\frac{x_{B2}}{y_{23}} \\ \therefore y_{23} अर्थात् \frac{6}{11} मुख्य अवयव है तथा \alpha_{1} अपगामी सदिश होगा।पुनः सामान्य रूपान्तरणों से नवीन आधारी हल के लिए निम्न सारणी होगी:
मुख्य अवयव वाली पंक्ति (Working rule):
द्वितीय प्रावस्था की प्रथम सारणी की द्वितीय पंक्ति मुख्य अवयव वाली पंक्ति है।अतः द्वितीय पंक्ति के अवयवों में मुख्य अवयव \frac{6}{11} का भाग देने पर द्वितीय सारणी की द्वितीय पंक्ति तैयार होगी:
\frac{1}{\frac{6}{11}}=\frac{11}{6}, \frac{1}{\frac{6}{11}}=\frac{11}{6}, \frac{0}{\frac{6}{11}}=0, \frac{\frac{6}{11}}{\frac{6}{11}}=1, \frac{\frac{1}{11}}{\frac{6}{11}}=\frac{1}{6}, \frac{-\frac{4}{11}}{\frac{6}{11}}=\frac{-2}{3}
प्रथम पंक्ति:द्वितीय प्रावस्था की प्रथम सारणी की प्रथम पंक्ति के अवयवों में से मुख्य अवयव वाली पंक्तियों के अवयवों अर्थात् उपर्युक्त अवयवों को मुख्य अवयव के संगत प्रथम पंक्ति के अवयव \frac{4}{11} से गुणा करके घटा देंगे:
1-\frac{11}{6} \times \frac{4}{11}=\frac{1}{3}, 0-\frac{11}{6} \times \frac{4}{11}=-\frac{2}{3}, 1-0 \times \frac{4}{11}=1, \\ \frac{4}{11}-1 \times \frac{4}{11}=0,-\frac{3}{11}-\frac{1}{6} \times \frac{4}{11}=-\frac{1}{3}, \frac{1}{11}-\left(-\frac{2}{3}\right) \frac{4}{11}=\frac{1}{3}
द्वितीय चरण:सारणी II

उपर्युक्त सारणी में Z_j-C_j के सभी मान ऋणेत्तर \left( \geq 0 \right) नहीं है,अतः आधारी हल इष्टतम नहीं है।नई सारणी के लिए प्रवेशी सदिश \alpha_{5} होगा,चूँकि Z_5^{*}-C_5=-\frac{7}{3} निम्नतम है।
\underset{i}{\text{निम्नतम}}\left\{\frac{x_{B i}}{y_{i 5}}, y_{i 5}>0\right\}=\underset{i}{\text{निम्नतम}}\left\{\frac{\frac{1}{3}}{\frac{1}{3}} \right\} \\ =\frac{x_{B1}}{y_{15}} \\ \therefore y_{15} अर्थात् \frac{1}{3} मुख्य अवयव है तथा \alpha_{2} अपगामी सदिश होगा।पुनः सामान्य रूपान्तरणों से नवीन आधारी हल के लिए निम्न सारणी होगी:
मुख्य अवयव वाली पंक्ति (Working rule):
मुख्य अवयव वाली पंक्ति प्रथम पंक्ति है।अतः द्वितीय चरण की द्वितीय सारणी के लिए प्रथम पंक्ति के अवयवों में मुख्य अवयव \frac{1}{3} का भाग देने पर तृतीय सारणी की प्रथम पंक्ति तैयार होगी:
\frac{\frac{1}{3}}{\frac{1}{3}}=1, \frac{-\frac{2}{3}}{\frac{1}{3}}=-2, \frac{1}{\frac{1}{3}}=3, \\ \frac{0}{\frac{1}{3}}=0, \frac{-\frac{1}{3}}{\frac{1}{3}}=-1, \frac{\frac{1}{3}}{\frac{1}{3}}=1
द्वितीय पंक्ति:द्वितीय सारणी की द्वितीय पंक्ति के अवयवों में से मुख्य अवयवों वाली पंक्ति के अवयवों अर्थात् उपर्युक्त अवयवों को मुख्य अवयव के संगत द्वितीय पंक्ति के अवयव -\frac{2}{3} से गुणा करके घटा देंगे:
\frac{1}{6}-1 \times \left(-\frac{2}{3}\right)=\frac{5}{2}, \frac{11}{6}-(-2) \times\left(-\frac{2}{3}\right) =\frac{1}{2}, \\ 0-3 \times\left(-\frac{2}{3}\right)=2,1-0 \times \left(-\frac{2}{3}\right)=1,\\ \frac{1}{6}-(-1) \times\left(-\frac{2}{3}\right)=-\frac{1}{2},-\frac{2}{3}-1 \times\left(-\frac{2}{3}\right)=0
द्वितीय चरण:सारणी III

चूँकि प्रत्येक Z_j-C_j \geq 0 हैं,अतः इसका आधारी हल इष्टतम होगा जो निम्न प्रकार है:
x_1=0, x_2=0, x_3=\frac{5}{2}, x_4=0, x_5=1
अतः दी गई समस्या का इष्टतम हल:
x_1=0, x_2=0, x_3=\frac{5}{2} है।
अधिकतम W=-2 x_1-9 x_1-x_3 \\ =-2 \times 0-9 \times 0-\frac{5}{2}=-\frac{5}{2}
अर्थात् निम्नतम Z=\frac{5}{2}
Example:2.निम्नतम (Min.) Z=\frac{15}{2} x_1-3 x_2
प्रतिबन्ध (s.t.) 3 x_1-x_2-x_3 \geq 3 \\ x_1-x_2+x_3 \geq 2
तथा (and) x_1, x_2, x_3 \geq 0
Solution:सर्वप्रथम उद्देश्य फलन को अधिकतमीकरण की समस्या में बदलते हैं।चूँकि यह निम्नतमीकरण की समस्या है,तत्पश्चात प्रतिबन्ध असमिकाओं में x_4 तथा x_5 आधिक्यपूरक चर घटाने पर समस्या का परिवर्तित रूप निम्न प्रकार होगा:
अधिकतम W=\frac{15}{2} x_1+3 x_2+0 x_3+0 x_4+0 x_5
प्रतिबन्ध 3 x_1-x_2-x_3-x_4+0 x_5=3 \\ x_1-x_2+x_3+0 x_4-x_5=2
तथा x_1, x_2, x_3, x_4, x_5 \geq 0
इस समस्या का प्रारम्भिक हल प्राप्त नहीं कर सकते।चूँकि इसके गुणांक मैट्रिक्स में एकिक उपमैट्रिक्स I_2 विद्यमान नहीं है,अतः उपर्युक्त समीकरणों में कृत्रिम चर x_6 तथा x_7 जोड़ते हैं तथा उद्देश्य फलन में इनके मूल्य -1 रखते हैं तथा कृत्रिम चरों के अतिरिक्त अन्य चरों का मूल्य शून्य रखने पर:
अधिकतम Z^*=0 x_1+0 x_2+6 x_3+0 x_4+x_5-x_6-x_7
प्रतिबन्ध 3 x_1-x_2-x_3-x_4+0 x_5+x_6+0 x_7=3 \\ x_1-x_2+x_3+0 x_4-x_5+x_6+x_7=2
तथा x_1, x_2, x_3, x_4, x_5, x_6, x_7 \geq 0
अब प्रतिबन्ध निकाय का गुणांक मैट्रिक्स
\left[\begin{array}{ccccccc} 3 & -1 & -1 & -1 & 0 & 1 & 0 \\ 1 & -1 & 1 & 0 & -1 & 0 & 1 \end{array}\right]=\left(\alpha_1 \alpha_2 \alpha_3 \alpha_4 \alpha_5 \alpha_6 \alpha_7\right) \\ \left(\alpha_6 \alpha_7\right)=I_{2} अतः प्रथम चरण की सारणी I का प्रारम्भिक आधार B=\left(\alpha_6 \alpha_7\right) तथा सारणी निम्न प्रकार होगी:
प्रथम चरण:सारणी I
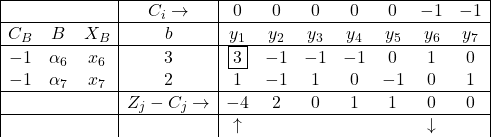
उपर्युक्त सारणी में Z_j^*-C_j के सभी मान ऋणेत्तर (Non Negative) नहीं है,अतः आधारी हल इष्टतम नहीं है।
Z_1^*-C_1=-4 निम्नतम है,अतः नये आधार के लिए \alpha_{1} प्रवेशी सदिश होगा।
\underset{i}{\text{निम्नतम}}\left\{\frac{x_{B i}}{y_{i 1}}, y_{i 1}>0\right\}=\underset{i}{\text{निम्नतम}}\left\{\frac{3}{3}, \frac{2}{1}\right\} \\ =\frac{3}{3} =\frac{x_{B1}}{y_{11}} \\ \therefore y_{11} अर्थात् 3 मुख्य अवयव तथा \alpha_{6} अपगामी सदिश होगा। \alpha_{6} चूँकि कृत्रिम चर है,अतः इसे नई सारणी में सम्मिलित नहीं करेंगे।अब सामान्य रूपान्तरणों से नवीन आधारी हल के लिए निम्न सारणी होगी:
प्रथम प्रावस्था:सारणी II

उपर्युक्त सारणी में Z_j^*-C_j के सभी मान ऋणेत्तर नहीं हैं।अतः आधारी हल इष्टतम नहीं है।नई सारणी के लिए \alpha_{3} प्रवेशी सदिश होगा चूँकि Z_3-C_3=-\frac{4}{3} निम्नतम है।
\underset{i}{\text{निम्नतम}}\left\{\frac{x_{B i}}{y_{i 3}}, y_{i 3}>0\right\}=\underset{i}{\text{निम्नतम}}\left\{\frac{1}{\frac{4}{3}}\right\} \\ =\frac{x_{B2}}{y_{23}} \\ \therefore y_{23} अर्थात् \frac{4}{3} मुख्य अवयव है तथा \alpha_{7} अपगामी सदिश होगा।चूँकि \alpha_{7} एक कृत्रिम चर है,अतः नई सारणी में इसे सम्मिलित नहीं करेंगे।पुनः सामान्य रूपान्तरणों से नवीन आधारी हल के लिए निम्न सारणी होगी:
प्रथम प्रावस्था:सारणी III

चूँकि Z_j^*-C_j \geq 0 तथा कोई भी कृत्रिम चर आधार में नहीं है,अतः प्रथम चरण इस स्थिति में समाप्त होता है।अतः इस सारणी से प्राप्त हल मूल समस्या का आधारी सुसंगत हल है।अब द्वितीय प्रावस्था (Phase II) में प्रवेश करते हैं।उद्देश्य फलन
W=-\frac{15}{2} x_1+3 x_2+0 x_3+0 x_4+0 x_5
द्वितीय चरण:सारणी I

चूँकि प्रत्येक Z_j^*-C_j \geq 0 है,अतः इसका आधारी हल इष्टतम होगा जो निम्न प्रकार है:
x_1=\frac{5}{4}, x_2=0, x_3=\frac{3}{4}, x_4=0, x_5=0
अतः दी गई समस्या का इष्टतम हल होगा:
x_1=\frac{5}{4}, x_2=0 तथा x_3=\frac{3}{4} है।
अधिकतम W=-\frac{15}{2} x_1+3 x_2+0 x_3 \\ =-\frac{15}{2} \times \frac{5}{4}+3 \times 0+0 \times \frac{3}{4} \\ =-\frac{75}{8}
अर्थात् निम्नतम Z=\frac{75}{8}
Example:3.अधिकतम (Max.) Z=10 x_1+9 x_2+7 x_2+x_4+5 x_5
प्रतिबन्ध (s.t.) -x_2+x_3+x_5=5 \\ x_1+x_2+x_3+x_5=5 \\ 2 x_1+3 x_2+4 x_3+x_4+x_5=10
तथा (and) x \geq 0, j=1,2,3,4,5
Solution:मानक रूप में रखने पर:
Max. Z=10 x_1+9 x_2+7 x_3+7 x_4+5 x_5
S.t. 0 x_1-x_2+x_3+0 x_4+x_5=5 \\ x_1+x_2+x_3+0 x_4+x_5=5 \\ 2 x_1+3 x_2+4 x_3+x_4+x_5=10
and x \geq 0 , j=1,2,3,4,5
उपर्युक्त समस्या में एकिक सदिश I_{3} विद्यमान नहीं है।अतः कृत्रिम चर x_6,x_7 तथा x_8 जोड़ते हैं तथा प्रथम प्रावस्था में उद्देश्य फलन में इनका मान -1 लेने तथा x_6,x_7 व x_8 के अतिरिक्त प्रत्येक चर का मान शून्य लेने पर दी गई समस्या का उद्देश्य फलन निम्न हो जाता है:
Max Z^*=0 x_1+0 x_2+0 x_3+0 x_4+0 x_5-x_6-x_7-x_8
s.t. 0 x_1-x_2+x_3+0 x_4+x_5+x_6+0 x_7+0 x_8=5 \\ x_1+x_2+x_3+0 x_4+x_5+0 x_6+x_7+0 x_8=5 \\ 2 x_1+3 x_2+4 x_3+x_4+x_5+x_6+0 x_7+x_8=10
and x_j \geq 0, j=1,2,3,4,5,6,7,8
अब प्रतिबन्ध निकाय का गुणांक मैट्रिक्स
\left[\begin{array}{cccccccc} 0 & -1 & 1 & 0 & 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 & 1 & 0 & 1 & 0 \\ 2 & 3 & 4 & 1 & 1 & 0 & 0 & 1 \end{array}\right]=\left(\alpha_1 \alpha_2 \alpha_3 \alpha_4 \alpha_5 \alpha_6 \alpha_7 \alpha_8 \right) \\ (\alpha_6 \alpha_7 \alpha_8)=I_{3} अतः प्रथम चरण की सारणी का प्रारम्भिक आधार B=(\alpha_6 \alpha_7 \alpha_8) तथा सारणी निम्न प्रकार होगी:
प्रथम प्रावस्था:सारणी I
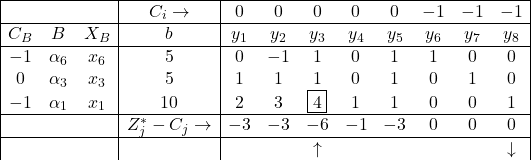
उपर्युक्त सारणी में Z_j^*-C_j के सभी मान ऋणेत्तर (Non Negative) नहीं है अतः आधारी हल इष्टतम नहीं है।
Z_3-C_3=-6 निम्मतम है,अतः नये आधार के लिए \alpha_3 प्रवेशी सदिश होगा:
\underset{i}{\text{निम्नतम}}\left\{\frac{x_{B i}}{y_{i 3}}, y_{i 3}>0\right\}=\underset{i}{\text{निम्नतम}}\left\{\frac{5}{1},\frac{5}{1},\frac{10}{4}\right\} \\ =\frac{10}{4}=\frac{x_{B3}}{y_{33}} \\ \therefore y_{33} अर्थात् 4 मुख्य अवयव तथा \alpha_8 अपगामी सदिश होगा।चूँकि \alpha_8 कृत्रिम चर है,अतः इसे नई सारणी में सम्मिलित नहीं करेंगे।अब सामान्य रूपान्तरणों से नवीन सारणी होगी:
प्रथम प्रावस्था:सारणी II

उपर्युक्त सारणी में Z_j^*-C_j के सभी मान ऋणेत्तर (Non Negative) नहीं है अतः आधारी हल इष्टतम नहीं है।
Z_5-C_5=-\frac{3}{2} निम्नतम है,अतः नये आधार के लिए \alpha_5 प्रवेशी सदिश हैगा।
\underset{i}{\text{निम्नतम}}\left\{\frac{x_{B i}}{y_{i 5}}, y_{i 5}>0\right\}=\underset{i}{\text{निम्नतम}}\left\{\frac{\frac{5}{2}}{\frac{3}{4}},\frac{\frac{5}{2}}{\frac{3}{4}}\right\}
चूँकि 1 निम्नतम मान है,अतः \alpha_6 तथा \alpha_7 दोनों ही अपगामी सदिश होंगे।यह अपभ्रष्टता विद्यमान होने का संकेत है।
केवल उन पंक्तियों के लिए जिनके अनुपात समान है।
निम्नतम {\frac{\text{प्रथम आधारी (Basis) स्तम्भ का अवयव}}{\text{मुख्य स्तंभ का संगत अवयव}}}
=निम्नतम{ \frac{y_6 \text{ के नीचे वाले स्तंभ का अवयव}}{y_5 \text{ के नीचे वाले स्तंभ का अवयव}} }
=निम्नतम \left\{ \frac{1}{\frac{3}{4}},\frac{0}{\frac{3}{4}} \right\} =\frac{0}{\frac{3}{4}}=\frac{x_{B2}}{y_{25}} \\ \therefore y_{25} अर्थात् \frac{3}{4} मुख्य अवयव तथा \alpha_7 अपगामी सदिश होगा।चूँकि \alpha_7 एक कृत्रिम चर है,अतः इसे नई सारणी में सम्मिलित नहीं करेंगे।अब सामान्य रूपान्तरणों से नवीन आधारी हल के लिए निम्न सारणी होगी:
प्रथम प्रावस्था:सारणी III
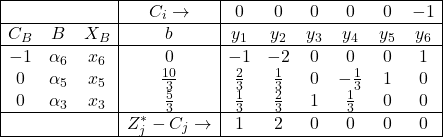
उपर्युक्त उदाहरणों के द्वारा एलपीपी को द्विप्रावस्था विधि द्वारा कैसे हल करें? (How to Solve LPP by Two Phase Method?) को समझ सकते हैं।
3.एलपीपी को द्विप्रावस्था विधि द्वारा कैसे हल करें पर आधारित सवाल (Questions Based on How to Solve LPP by Two Phase Method?):
(1.)निम्न रैखिक प्रोग्रामन समस्या को द्विप्रावस्था विधि से हल करिए:
(Solve the following L. P. P. by two phase method):
निम्नतम (Min.) Z=x_1+x_2
प्रतिबन्ध (s.t.) 2x_1+x_2 \geq 4 \\ x_1+7 x_2 \geq 7
तथा (and) x_1, x_2 \geq 0
(2.)निम्न रैखिक प्रोग्रामन समस्या को द्विप्रावस्था विधि से हल करिए:
(Solve the following L. P. P. by two phase method):
निम्नतम (Min.) Z=3x_1+2x_2
प्रतिबन्ध (s.t.) 2x_1+x_2 \leq 2 \\ 3x_1+4x_2 \geq 12
तथा (and) x_1, x_2 \geq 0
उत्तर (Answers):(1.) x_1=\frac{21}{13}, x_2=\frac{10}{13} ,min Z=\frac{31}{13}
(2.)कोई सुसंगत हल नहीं
उपर्युक्त सवालों को हल करने पर एलपीपी को द्विप्रावस्था विधि द्वारा कैसे हल करें? (How to Solve LPP by Two Phase Method?) को ठीक से समझ सकते हैं।
Also Read This Article:- How to Solve LPP with Simplex Method?
4.एलपीपी को द्विप्रावस्था विधि द्वारा कैसे हल करें? (Frequently Asked Questions Related to How to Solve LPP by Two Phase Method?),रैखिक प्रोग्रामन समस्याओं को द्विप्रावस्था विधि से हल करना (To Solve Linear Programming Problems by Two Phase Method) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.प्रतिबन्धों को समीकरणों में कैसे बदलते हैं? (How to Convert Constraints in Equations?):
उत्तर:यदि कोई प्रतिबन्ध असमिका के रूप में हो तो उसे न्यूनतापूरक अथवा आधिक्यपूरक चर की सहायता से समीकरण में बदलते हैं।इन न्यूनतापूरक अथवा आधिक्यपूरक चरों को शून्य मूल्य सहित उद्देश्य फलन में भी सम्मिलित करते हैं।
प्रश्न:2.कब और क्यों कृत्रिम चर का प्रयोग करते हैं? (When and Why Artificial Variable is Used?):
उत्तर:प्रारम्भिक आधार के निर्धारण हेतु आवश्यकतानुसार कृत्रिम चरों को सम्मिलित कर प्रतिबन्ध निकाय को मैट्रिक्स AX=b में व्यक्त करते हैं।इन कृत्रिम चरों के संगत उद्देश्य फलन में इनके मूल्य -M को सम्मिलित करते हैं,जहाँ M एक बहुत बड़ी धनात्मक संख्या है।
प्रश्न:3.रैखिक प्रोग्रामन समस्या में अतिरिक्तता से आप क्या समझते हैं? (What Do You Mean by Redundancy in LPP?):
उत्तर:जब प्रतिबन्ध समीकरणों द्वारा सुसंगत हल प्राप्त न हो तथा प्रतिबन्धों की संख्या आवश्यकता से अधिक हो।
उपर्युक्त प्रश्नों के उत्तर द्वारा एलपीपी को द्विप्रावस्था विधि द्वारा कैसे हल करें? (How to Solve LPP by Two Phase Method?),रैखिक प्रोग्रामन समस्याओं को द्विप्रावस्था विधि से हल करना (To Solve Linear Programming Problems by Two Phase Method) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
How to Solve LPP by Two Phase Method?
एलपीपी को द्विप्रावस्था विधि द्वारा कैसे हल करें?
(How to Solve LPP by Two Phase Method?)
How to Solve LPP by Two Phase Method?
एलपीपी को द्विप्रावस्था विधि द्वारा कैसे हल करें? (How to Solve LPP by Two Phase Method?)
इस आर्टिकल में इसी द्विप्रावस्था विधि के द्वारा एलपीपी के सवालों को हल किया गया है।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.








