When mathematics screws you over
जब मैथ्स आपके ऊपर शिकंजा कसेगा का परिचय (Introduction to When Mathematics Screws You Over):
- जब मैथ्स आपके ऊपर शिकंजा कसेगा (When Mathematics Screws You Over) के इस आर्टिकल में बताया गया है एक वृत्त पर एक बिंदु,दो बिंदु,तीन बिंदु,चार बिंदु,पाँच बिंदु,छ्ह बिंदु लेने पर वृत्त अपना पैटर्न बदलता रहता है.
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:How mathematicians and designers improve the quality of our lives
1.जब मैथ्स आपके ऊपर शिकंजा कसेगा (When mathematics screws you over):
- रीजनिंग गणित की भाषा है
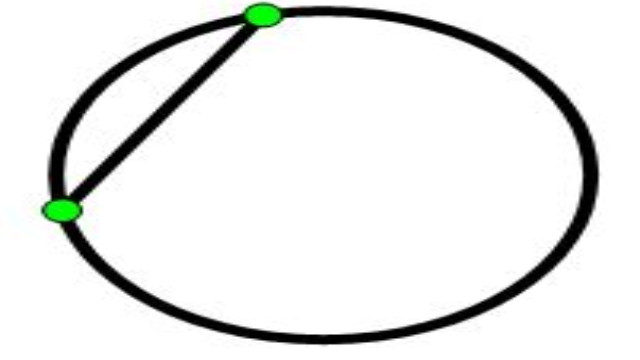
एक दिलचस्प पैटर्न है जिसमें एक वृत्त पर अंक शामिल हैं। हम परिधि पर एक बिंदु से शुरू करते हैं।
- अब एक दूसरा बिंदु जोड़ते हैं और उन्हें जोड़ते हैं। हमने सर्कल को दो क्षेत्रों में विभाजित किया है:
- एक तीसरा बिंदु जोड़ें और दोहराएं।
- चार क्षेत्र। किसी भी विचार जब हम चार अंक लेंगे तो क्या होगा? यह सही है, हम 8 क्षेत्रों के साथ समाप्त होते हैं।
- क्या आपको पैटर्न मिला है? बेशक आपके पास है; हर बार क्षेत्रों की संख्या दोगुनी हो रही है। यह समझ में आता है। यदि आप अभी भी संदेह में हैं, तो अगले एक के साथ प्रयास करें:
- उत्कृष्ट, हमें उम्मीद के मुताबिक 16 क्षेत्र मिलते हैं।
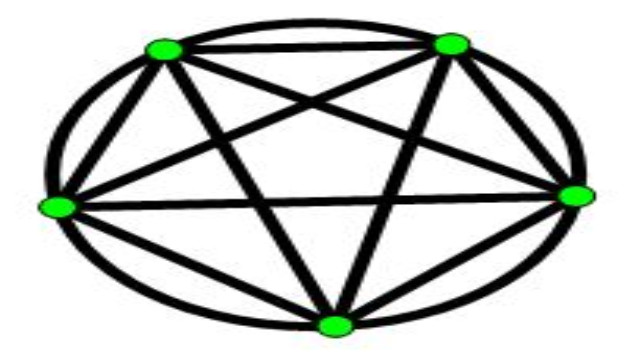
अब तक आप जान जाएंगे कि 6 बिंदुओं के लिए क्या अपेक्षा है – डबल 16, या 32. क्या आप एक सट्टेबाजी व्यक्ति हैं? 32 क्षेत्रों को लौटाने वाले अगले सर्कल पर आप कितना जुआ खेलेंगे? यहाँ जाता है – उन्हें गिनें:
- क्या आपने रीटेक किया? मैं भी; मैं इस पर विश्वास नहीं कर सकता था। निश्चित रूप से मैं एक को याद नहीं कर रहा हूं – 31 क्षेत्रों में समाप्त होने का कोई तरीका नहीं है। निश्चिंत रहें, आपकी आँखों ने आपको धोखा नहीं दिया है। दूसरी ओर आपका गणितीय तर्क …
Also Read This Article:Screw theory
2. मैथ्स की खूबसूरती इसके पैटर्न में है (The beauty of mathematics is in its patterns):
- हमें 32 क्षेत्रों की उम्मीद क्यों थी? सबसे अधिक संभावना है क्योंकि यह एक पैटर्न जारी रखता है जिस पर हम ठोकर खा चुके हैं। हमारे दिमाग पैटर्न से जुड़े होते हैं; हम सहज रूप से उन्हें खोजते हैं। प्रत्येक नए सर्कल ने हमारे विश्वास प्रणाली को मजबूत किया, तेजी से।
- लेकिन यह सब था; एक धारणा है। कोई कठोर तर्क नहीं था, कोई ठोस तर्क नहीं था जो कि क्षेत्रों को दोगुना करने के लिए ठहराया। मैथ्स की खूबसूरती इसके पैटर्न में है। लेकिन इसके साथ ही इसका खतरा भी है। मैथ्स पैटर्न मान्यता से अधिक है। यह समझने के बारे में भी है कि वे पैटर्न क्यों पकड़ते हैं।
- वह तर्क जहां पर आता है। हम गणित के अकाट्य सत्य को केवल तभी मना सकते हैं जब हम अपने बकाये का भुगतान करते हैं और स्वयं को दोषरहित तर्क के माध्यम से आश्वस्त करते हैं कि वे ऐसा कर रहे हैं। मैथ्स आपके परिश्रम को पुरस्कृत करेगा, लेकिन यदि आप कारण को छोड़ देते हैं, तो यह आपको उतना ही खराब कर देगा।
सर्कल क्षेत्रों में एक और पैटर्न है, एक जो केवल दोहरीकरण की तुलना में वर्णन करना अधिक कठिन है? संभवत:; आप इस स्तर पर पर्याप्त देखभाल नहीं कर सकते हैं। शायद आप काफी घायल हो गए हैं। फिर भी, यदि आपकी जिज्ञासा काट रही है, तो आप नए हाइपोथीसिस विकसित करने और परीक्षण करने के साथ-साथ अगले सर्कल को ड्रॉ करना चाहते हैं। हो सकता है कि एक सूक्ष्म पैटर्न सब के बाद गुप्त हो।
अब निम्नलिखित पर विचार करें:
n + n + 41 - जब भी n एक ऋणात्मक पूर्णांक है, मैं इस अभिव्यक्ति को एक प्रमुख संख्या देता है। मुझे विश्वास नहीं है? कोशिश करके देखो।
- जब n = 0, यह 41 देता है। अच्छी शुरुआत।
N = 1 के लिए हमें 43 मिलता है और n = 2 के लिए हमें 47 मिलता है। दोनों प्राइम। - मेरा दावा आशाजनक लग रहा है। आपको संदेह करने का हर अधिकार है; वृत्ताकार क्षेत्रों की पीड़ा के बाद मुझे कुछ कम होने की उम्मीद नहीं है। और यदि आप कुछ भी जानते हैं, तो यह है कि वे एक रहस्यमय प्रजाति हैं। निश्चित रूप से हम इतनी आसानी से उनकी अनंत आपूर्ति नहीं कर सकते।
- लेकिन आप मेरे दावे को कैसे अस्वीकार करेंगे? आपको एक प्रतिसाद खोजना होगा; पूर्णांक n का एक उदाहरण जिसके लिए अभिव्यक्ति n of + n + 41 अभाज्य नहीं है। यदि आप बदले में प्रत्येक पूर्णांक की कोशिश करने के व्यवस्थित दृष्टिकोण का चुनाव करते हैं, तो आप यहां कुछ समय के लिए हो सकते हैं। वास्तव में, अभिव्यक्ति n = 40 तक primes वापस आ जाएगी।
- हम अभिव्यक्ति पर थोड़ा और प्रतिबिंबित करके एक प्रतिसाद पैदा कर सकते हैं। क्या आप देख सकते हैं कि यह n = 41 के लिए प्रमुख क्यों नहीं हो सकता है? एक कारण यह है कि अभिव्यक्ति में प्रत्येक शब्द 41 से विभाज्य है, जिसका अर्थ है 41 पूरे अभिव्यक्ति का एक कारक है। यदि यह मामला है तो निश्चित रूप से यह प्रमुख नहीं हो सकता है! मेरा दावा उजागर हुआ; यह केवल उल्लेखनीय है जब तक यह n = 40 तक आयोजित नहीं हुआ।
प्रत्येक पूर्णांक की जांच करने की ब्रूट-फोर्स विधि में अभिव्यक्ति से n = 41 लेने की लालित्य पर कुछ भी नहीं है। रीज़निंग ब्यूटी है। - स्कूली पाठ्यक्रम में रीजनिंग को अधिक एयरटाइम मिल रहा है, और काफी हद तक सही भी है। यह अक्सर एक आत्म-निहित विषय के रूप में देखा जाता है, जो अन्य सभी से अलग रखा जाता है। Something कोर ’सामग्री को कवर करने के बाद, शुक्रवार के लिए कुछ अतिरिक्त। या उन तथाकथित प्रतिभाशाली छात्रों को चुनौती देने के लिए कुछ।
- यहाँ रगड़ है: तर्क गणित की भाषा है। यह है कि हम कुछ भी सुनिश्चित कर सकते हैं। गणित की क्या और कैसे महत्वपूर्ण हैं, लेकिन दोनों ही बिना अर्थ के क्यों हैं। किसी भी मैथ्स के छात्र से जो सबसे महत्वपूर्ण सवाल पूछा जा सकता है, वह क्यों है? आपके गणितीय तर्कों को सख्ती से सही ठहराने में सक्षम होने के अलावा और अधिक सशक्त नहीं है। यह आपको उस ज्ञान का स्वामित्व देता है; हमारे बीच सबसे कठोर भी नहीं ध्वनि तर्क हो सकता है। प्रत्येक अवधारणा के सीखने और सिखाने में तर्क का उपयोग किया जाना चाहिए।
- गणित वह विषय है जो हमेशा देता है। लेकिन जब हम इसे ले लेंगे तो यह आसानी से हमें भटका देगा। हम धर्मी मार्ग पर रहेंगे, और अपने छात्रों का मार्गदर्शन करेंगे, इसलिए जब तक हम यह पूछने का अपना अधिकार बरकरार रखते हैं कि क्यों?
Also Read This Article:why did I have to learn calculus
- उपर्युक्त आर्टिकल में जब मैथ्स आपके ऊपर शिकंजा कसेगा (When Mathematics Screws You Over) के बारे में बताया गया है.
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |