Probability Philosophical Perspective
1.प्रायिकता:एक दार्शनिक परिप्रेक्ष्य का परिचय (Introduction to Probability Philosophical Perspective),(Probability A Philosophical Perspective):
- प्रायिकता:एक दार्शनिक परिप्रेक्ष्य (Probability Philosophical Perspective) के इस आर्टिकल में बताया गया है कि प्रायिकता हमें संभावित दुनिया के बारे में बताती है।जीवन में हमारे साथ घटित होनेवाली घटनाओं के परिणाम का पूर्वानुमान लगाने में मदद करती है।हालांकि कि इस निर्धारक दुनिया में किसी घटना को देखने के बारे में अलग-अलग व्यक्तियों के अलग-अलग दृष्टिकोण हो सकते हैं।
- जीवन के प्रत्येक क्षेत्र में भावी अनिश्चितताओं के मध्य मनुष्य को अनेक निर्णय लेने पड़ते हैं। अनिश्चित घटनाओं के प्रति अपना अनुमान हम ‘सम्भावना’ या ‘प्रायिकता’ के रूप में व्यक्त करते हैं। उदाहरणार्थ सिक्का उछालने पर उसके चित्त (Head) गिरने की सम्भावना \frac{1}{2} है, चुनाव में निर्दलीय प्रत्याशी के विजय होने की बहुत कम प्रायिकता है, अगले दशक में मंगल ग्रह पर पहुँचने की 90% सम्भावना है, आगामी अन्तर्राष्ट्रीय ओलंपिक खेलकूद में भारत के हाॉकी में स्वर्णपदक जीतने की 60% प्रायिकता है इत्यादि। सामान्य भाषा में सम्भावना या प्रायिकता शब्द द्वारा घटनाओं की अनिश्चितता की अभिव्यक्ति होती है परन्तु सांख्यिकी में इस शब्द का विशिष्ट अर्थ है और सुनिश्चित गणितीय विधियों से घटनाओं की प्रायिकता के संख्यात्मक माप का परिगणन किया जाता है। अतः सांख्यिकीय या गणितीय अर्थ में प्रायिकता कोरी अटकल-मात्र या कोई भावनात्मक कथन नहीं है वरन् इस धारणा का एक स्पष्ट वैज्ञानिक आधार है।
- ऐतिहासिक विकास एवं महत्त्व (Historical Development and Importance):
प्रायिकता सिद्धान्त के विधिवत अध्ययन की प्रेरणा सर्वप्रथम सत्रहवीं शताब्दी में यूरोप के जुआरियों और सटोरियों की ओर से आई थी जिन्होंने भाग्यलक्ष्मी (Goddess Fortune) की चपलता से निराश होकर उस युग के प्रसिद्ध गणितज्ञों (जैसे गैलीलियो गैलिली, पास्कल, फरमैट, कारडेनो, आदि) से द्यूत-क्रीडा सम्बन्धी समस्याओं के समाधान के लिए परामर्श लेना प्रारम्भ किया। इन विद्वानों के गणितीय अध्ययनों से ही प्रायिकता सिद्धान्त का प्रादुर्भाव हुआ। अठारहवीं शताब्दी और उन्नीसवीं शताब्दी में लाॅप्लेस, गाॅस बरनौली, यूलर आदि गणित शास्त्रियों ने इस सिद्धान्त के विकास में महत्त्वपूर्ण योग दिया। कुछ विशेषज्ञों ने राजनीतिक, सैनिक, वित्तीय, आर्थिक एवं व्यावसायिक क्षेत्रों में इस सिद्धांत को सफलतापूर्वक प्रयोग किया। बीसवीं शताब्दी में रोनेल्ड फिशर, कार्ल पियर्सन, स्नूडेकोर, गैसेट, नीमेन आदि विद्वानों ने प्रायिकता सिद्धान्त पर आधारित प्रतिचयन-सिद्धान्त, क्रीड़ा-सिद्धान्त, निर्णय सिद्धान्त पर महत्त्वपूर्ण कार्य किया है। आजकल प्रायिकता सिद्धान्त की उपयोगिता जुआरियों, ताश खेलनेवालों, पासा फेंकनेवालों व सटोरियों तक ही सीमित नहीं है। एमाइल बोरेल के अनुसार, प्रायिकता सिद्धान्त केवल अपने जन्मदाताओं-ताश खेलनेवालों व पासा फेंकनेवालों के लिए ही रुचि का विषय नहीं रहा है, अपितु उन सभी कार्यशील व्यक्तियों, उद्योग के अध्यक्षों अथवा सेनाध्यक्षों के लिए महत्त्वपूर्ण है जिनकी सफलता उचित निर्णयों पर आश्रित होती है और भविष्य के लिए अनुमान लगाने आवश्यक होते हैं। सांख्यिकीय आगमन और प्रतिचयन के आधार पर निकाले गये निष्कर्ष के रूप में व्यक्त किए जाते हैं निश्चितता के रूप में नहीं। दैव पर आधारित क्रीड़ाओं प्राकृतिक व भौतिक विज्ञानों और अर्थशास्त्र, व्यवसाय प्रबंधन, बीमा व्यवसाय आदि से सम्बन्ध विभिन्न निर्णय प्रायिकता सिद्धान्त के आधार पर ही लिए जाते हैं। कैने व कीपिंग के शब्दों में ‘प्रायिकता सिद्धान्त’ आधुनिक गणित की अत्यंत रोचक शाखाओं में से एक है और ज्ञान के अनेक क्षेत्रों में अनुप्रयोगों के लिए महत्त्वपूर्ण है। यह केवल बीमा-सिद्धान्त व सांख्यिकी में ही नहीं अपितु प्राणिशास्त्र और भौतिक विज्ञानों की अनेक शाखाओं में आधारभूत महत्त्व रखता है। काॅक्सडेन के अनुसार प्रायिकतात्मक तर्क का प्रयोग जुआ, बीमा, सैद्धान्तिक भौतिकी, प्राणिशास्त्र, अर्थशास्त्र तथा ऐसे ही अनेक क्षेत्रों में किया जाता है। - आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
2.प्रायिकता:एक दार्शनिक परिप्रेक्ष्य (Probability Philosophical Perspective),(Probability:A Philosophical Perspective):
- यह संभवता की नींव को देखते हुए श्रृंखला में पहला निबंध है और यह कुछ संभावित तर्कसंगतताओं की खोज करता है।दूसरा निबंध एक अवधारणा के रूप में सभी प्रायिकता की आलोचना करेगा।
अनुभवजन्य ज्ञान को डेटा बिंदुओं के अवलोकन से प्राप्त किया जाता है और फिर वितरण का निर्माण किया जाता है (भले ही वे अंतर्निहित रूप से निर्मित हों)। इसका अर्थ यह निकलता है कि अनुभवजन्य ज्ञान असंभव है-कम से कम बिना कारण या पूर्व-निर्धारित ज्ञान के पादरियों के बिना। (पिछले अनुभव से संकेत मिलता है कि मनुष्य केवल अमूर्त कारण से काम करने में इतना अच्छा नहीं है इसलिए ज्ञान के लिए संभावनाएँ मंद हैं)
3.प्रेरणा (Motivation):
- प्रायिकता की परिभाषाएँ बहुत मायावी हैं।गणितीय रूप से,परिभाषा इतनी कठिन नहीं है और प्रायिकता के प्रश्न एक सेट में ‘समान रूप से संभावित’ परिणामों की संख्या गिनने के लिए उबलते हैं।गणित से परे,यह स्पष्ट नहीं है कि संभावना क्या है।
- सभी संभावित कारणों पर किन संभावनाओं का महत्वपूर्ण प्रभाव पड़ता है।भगवान के लिए ठीक-ठीक तर्क पर विचार करें।इस कदम में निहित है कि स्थिरांक अविश्वसनीय रूप से ‘के लिए ट्यून है’इसलिए यह भगवान के बिना होने की प्रायिकता नहीं है ‘प्रायिकता की गणितीय परिभाषा हमें विफल हो जाती है।
- गणितीय रूप से,जो अभी हुआ है वह सरल बायेसियन प्रायिकता है।यदि हमारे पास मौजूदा ‘परमात्मा ‘ की प्रायिकता के लिए एक वितरण है (और तब वह ठीक-ठीक स्थिरांक का उपयोग करके जीवन का निर्माण कर रहा है) और उन मूल्यों के लिए एक प्रायिकता वितरण जो भौतिक स्थिरांक ले सकते हैं यदि भगवान मौजूद नहीं हैं,तो हम निर्माण कर सकते हैं परमात्मा ’के परिणामस्वरूप जीवन का नमूना स्थानों की तुलना करें और यादृच्छिकता’ के परिणामस्वरूप कितने का निर्माण किया।
- लेकिन स्पष्ट रूप से यह बकवास है। किसी चीज़ के लिए प्रायिकता वितरण जो एक आवश्यक वस्तु है? (इसके अलावा,हम भौतिक स्थिरांक के लिए प्रायिकता वितरण कैसे बना सकते हैं?)।पूर्व मामले में एक प्रायिकता वितरण शुद्ध यादृच्छिकता ’(जो भी मतलब हो) का प्रतिनिधित्व नहीं कर सकता है।बल्कि ऐसा लगता है,यदि ऐसा कोई वितरण मौजूद था तो यह अनिश्चितता का सूचक होगा लेकिन विभिन्न परिणामों का नहीं।इस मामले में, संभावित परिणामों का कोई ‘नमूना स्थान’ नहीं है!
- शायद प्रायिकताको यहां लागू नहीं किया जा सकता है -हालांकि यह जीवन के सबसे बड़े दार्शनिक सवालों में से एक के बारे में सबूत देने के लिए असंतोषजनक है।विज्ञान के बारे में क्या? क्या प्रायिकता है कि, नियमों का एक वास्तविक सेट दिया गया है जो ब्रह्मांड का वर्णन करता है, पर्याप्त प्रयोग और छेड़छाड़ नियमों के गलत सेट के कारण हो सकता है, जिसमें से बहुत कुछ बता सकता है-लेकिन कुछ बिंदु पर एक ब्लॉक में चल रहा है और आगे की प्रगति की ओर इशारा करता है।यह एक ऋणात्मक ढाल के साथ रास्ता निकालकर एक न्यूनतम बिंदु खोजने के लिए महत्वपूर्ण होगा, जो स्थानीय मिनीमाता को ढूंढ सकता है लेकिन जरूरी नहीं कि वैश्विक मिनीमा।यदि आप शब्दावली से परिचित हैं,तो यह सादृश्य मदद कर सकता है: यदि पहाड़ों की एक श्रृंखला है, तो हमेशा ऊपर की ओर चलना आपको एक पहाड़ की चोटी पर जाने के लिए सुनिश्चित करेगा, लेकिन जरूरी नहीं कि सबसे ऊंचे पर्वत के ऊपर।
(यह। ग्रेडिएंट डिसेंट ’जो विज्ञान करता है।यह अवलोकन करता है फिर अवलोकन के साथ संगतता में सुधार करने के लिए अपने सिद्धांतों को बदलता है)। क्या हम संभव वैज्ञानिक सिद्धांतों का एक वितरण है जो हम भर में ठोकर खा सकते हैं? - बहुत कम से कम, इससे यह स्पष्ट होता है कि हमारी वर्तमान समझ और संभावनाओं का निरूपण कितना अपर्याप्त है।सिर्फ इसलिए कि चीजों ने काम किया है ’हमें इन कठिन सवालों को पूछने की जरूरत नहीं है।
4.एक नियतात्मक दुनिया में प्रायिकता (Probability in a deterministic world):
- एक ऐसे खेल पर विचार करें जहां कोई दूसरा 1 से n तक पूर्णांक चुनता है और आप इसका अनुमान लगाने की कोशिश करते हैं।उस व्यक्ति द्वारा ‘बिंदु बेतरतीब ढंग से’ चुनने से हमारा क्या मतलब है? यह संभव है कि, पर्याप्त जानकारी के साथ,आप पूरी तरह से चुन सकते हैं कि एक यादृच्छिक संख्या जनरेटर (या व्यक्ति) क्या उठाएगा।इस मामले में, हम संभावनाओं का उपयोग तंत्र के बारे में सीमित जानकारी के मॉडल के रूप में करते हैं।
- पर्याप्त टिप्पणियों के साथ,यह इन अज्ञात कारणों का शुद्ध प्रभाव प्रकट करता है, यह है कि प्रत्येक संख्या को अक्सर उठाया जाता है। एक नियतात्मक दुनिया में,कई संभावनाएँ नहीं हैं। प्रत्येक संख्या के लिए \frac{1}{n} की प्रायिकता के साथ आप जो वितरण करते हैं, उसमें एक सही परिणाम की भयानक गणितीय भविष्यवाणी होती है, जो केवल नियतात्मक दुनिया में अनिवार्य रूप से होने के बावजूद मॉडल में \left(\frac{1}{n}\right)^k बार होता है।
- बता दें कि स्टीव एक्स-वाई प्लेन में रहता है। मैं धीरे-धीरे सह-निर्देशांक को पूर्व-निर्धारित तरीके से \sin{x}के ग्राफ (x) में रखता हूं।हालाँकि, वह पूरे ग्राफ को कभी नहीं देखता है,इसलिए \sin{x}¸ कभी भी निश्चितता के साथ यह निष्कर्ष नहीं निकाल सकता है कि यह \sin{x} है, जैसा कि अंकों के दिए गए सेट के माध्यम से होने वाली अन्य बहु संख्याओं के विपरीत है। इस बात को समझना कि जब तक उसके पास पुजारी नहीं होंगे, तब तक किसी भी चीज के बारे में निश्चित नहीं होगा।वह केवल कभी-कभी परिमित डेटा बिंदुओं को देखता है-अपने दृष्टिकोण से, किसी भी क्षण एक गलत बिंदु परिकल्पना को बर्बाद कर सकता है कि रेखा \sin{x} है। ऊपर जो मैं कर रहा हूं उसके ज्ञान के बदले में, वह वास्तव में अनिश्चित रहेगा।
- नियतात्मक दुनिया में,हम स्टीव हैं! केवल तभी जब हम सभी डेटा पॉइंट्स का निरीक्षण कर सकते हैं,अनिश्चितता गायब हो जाती है।लेकिन यह असंभव है।
- क्या स्टीव उन बिंदुओं से परे ग्राफ के बारे में वैध कटौती कर सकता है जो वह देखता है?
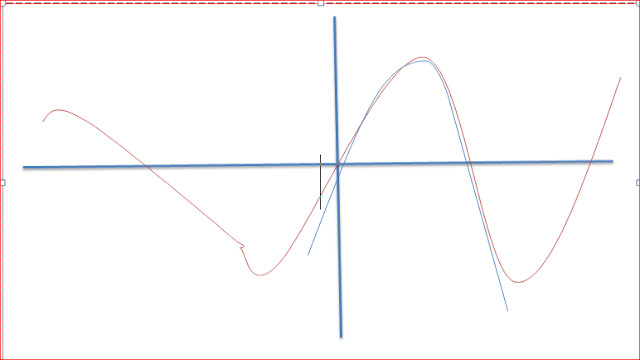
- विज्ञान में ध्यान दें कि हम अनिवार्य रूप से रखे गए बिंदुओं को देखते हैं और समीकरणों को एक्सट्रपलेट करते हैं।क्या भविष्य कहनेवाला शक्ति एक अच्छा पर्याप्त परीक्षण है? क्या होगा अगर स्टीव को sin{x} देखने के लिए पसंद किया गया था,लेकिन मैं वास्तव में मनाया डेटा बिंदु के लिए एक बहुपद को \sin{x} के बहुत नीचे रख रहा था? नीचे दी गई तस्वीर इस बात का उदाहरण देती है कि हम कुछ डेटा बिंदुओं के आधार पर गलत फ़ंक्शन की आसानी से भविष्यवाणी कैसे कर सकते हैं। ब्लू फंक्शन सीमा में \sin{x} के लिए एक उत्कृष्ट सन्निकटन है-यदि आपने डेटा रेंज का एक सेट उस सीमा में एक संबंध दिखाते हुए देखा,तो आप यह कैसे जानेंगे कि वास्तविक संबंध कौन से कार्य थे?
5.वास्तविक यादृच्छिकता ’वाले विश्व में प्रायिकता (Probability in a world with real ‘randomness’):
- अर्थात।कई परिणाम संभव हैं।
- यह ध्यान देने योग्य है कि दो दुनिया-प्रायिकता दुनिया और निर्धारक दुनिया – हमारे परिप्रेक्ष्य में पूरी तरह से समान हैं।उत्तरार्द्ध में हम यह नहीं जान सकते हैं कि प्रत्येक डेटा बिंदु निर्धारक नहीं था,ठीक वैसे ही जैसा कि पूर्व में हम नहीं जानते थे कि यादृच्छिकता का एक वास्तविक तत्व नहीं था।यादृच्छिकता की दुनिया में, मान लें कि हम निर्धारक दुनिया में रहते थे:डेटा बिंदुओं का कोई भी सेट सुसंगत है।
- इसका क्या मतलब है? क्या कई जगहें वास्तव में हर बार एक बेतरतीब घटना होती हैं (और क्या यह निर्धारक है कि हम किस में उतरते हैं)? यहां मुद्दा यह है कि दुनिया में सच्चे यादृच्छिक चर को समझने का प्रयास हमेशा अपने गणितीय गुणों (जो पहली जगह में वास्तविक दुनिया की घटनाओं से प्राप्त करने के लिए किया गया था) को वापस करने की अपील करता है।
- हम दुनिया में किसी चीज़ को एक नंबर दे रहे हैं, इसलिए हमें पता होना चाहिए कि संख्या क्या प्रतीक है।
यदि हम अभी तक यादृच्छिक चर की अस्पष्ट समझ का उपयोग करते हैं, तो हमें एक महत्वपूर्ण बिंदु मिलता है।
गणित में, हम अक्सर वितरण के साथ शुरू करते हैं और परिणामों के बारे में कटौती करते हैं। - वास्तविक जीवन में, हमारे आस-पास की दुनिया के मॉडल का निरीक्षण करें और धीरे-धीरे बनाएं। (उदाहरण:किसी व्यक्ति द्वारा बहुत से लोगों के साथ दुर्व्यवहार किया गया है,जो कि गुमराह हुए लोगों की तुलना में लोगों की विश्वसनीयता के लिए एक अलग वितरण होगा।शायद इसलिए बच्चे अधिक विश्वास करते हैं।) जब हम केवल डेटा बिंदु देखते हैं और परिणाम नहीं।हम कभी नहीं जानते कि यह वितरण क्या है।
6.सांख्यिकीय अनुमान; पुरोहितों की आवश्यकता (Statistical inference; the necessity of priors):
- अंत में हमें जो मिलता है वह ज्ञान की असंभवता है।हम आम तौर पर कुछ पुजारियों के प्रति विकासवादी प्रवृत्ति से बचते हैं।
- निम्नलिखित को धयान मे रखते हुए:
दो लोगों ने एक घटना को देखा, और एक दूसरे को नहीं जानते।
मैं उनमें से एक से पूछताछ करता हूं, जो कहता है कि A हुआ। - मैं अनिश्चित हो सकता हूं कि क्या हुआ – क्या यह व्यक्ति झूठ बोल रहा है? अगर मुझे लगता है कि उनके पास झूठ बोलने का कोई अच्छा कारण नहीं था (प्रभाव में वितरण के बारे में कि क्या वे झूठ बोलने वाले व्यक्ति के प्रकार हैं) तो शायद मैं संतुष्ट हूं।
- मैं दूसरे से पूछताछ करता हूं, जो यह भी कहता है कि A हुआ।
यह मुझे आश्वस्त करता है, क्योंकि मेरे मस्तिष्क में झूठ की घटनाओं के बारे में एक पूर्व वितरण है।जब तक मेरे पास यह सोचने का अच्छा कारण नहीं है कि उन्होंने सहयोग किया,यह संभवतः वास्तविक घटना है। - हम केवल डेटा बिंदुओं का पालन करते हैं और चाहे वह दुनिया के बारे में एक विश्वास का समर्थन करता है एक अंतर्निहित वितरण पर निर्भर करता है।कई डेटा बिंदुओं के साथ हम एक वितरण बनाते हैं।हालाँकि,वितरण बनाने के लिए हमें वितरण के वितरण पर विचार करना होगा। वितरण देने का हमारा तर्क अनिवार्य रूप से एक है-यानी कि किस हद तक मॉडल डेटा के अनुरूप होगा।हालाँकि,मॉडल के सही होने के बारे में हमारा विश्वास मॉडल के वितरण पर निर्भर होना चाहिए! एक कृत्रिम उदाहरण में, यदि कंप्यूटर ने मीन 0 के साथ एक सामान्य वितरण बनाया है, तो x का प्रत्येक मान एक सामान्य चर का वर्णन करने वाले सामान्य वितरण के माध्यम का प्रतिनिधित्व करता है,तो यदि आपके डेटा का अर्थ 3 है,तो अंतर्निहित वितरण के लिए सबसे अच्छा अनुमान सामने आने वाला है। 0 की ओर थोड़ा तिरछा होना,क्योंकि यह वह जगह है जहाँ प्रायिकता का सबसे बड़ा द्रव्यमान है: अंतर्निहित वितरण है।
- आप वितरण के बारे में वितरण की आवश्यकता से इनकार कर सकते हैं।लेकिन दोनों मामलों में (यादृच्छिक और निर्धारक) वितरण निर्धारण प्रणाली के बारे में हमारी अनिश्चितता या सही यादृच्छिकता के साथ एक प्रणाली में शामिल प्रायिकताओं को निर्धारित करने के लिए हमारी विधि है।इसलिए यदि आप वितरण के लिए वितरण की मात्रा निर्धारित नहीं करते हैं तो आप अनिश्चितता या यादृच्छिकता के बारे में अनिश्चित रहते हैं। अर्थात।आपने कोई महामारी संबंधी प्रगति नहीं की है।
- यह तर्क वितरण के लिए वितरण पर लागू किया जा सकता है। लेकिन अब तक हम एक डेटा बिंदु के साथ सांख्यिकीय निष्कर्ष निकालने की कोशिश कर रहे हैं। (तर्क का तात्पर्य अभी भी एक अनंत प्रतिगामी है।)
7.निष्कर्ष? (Conclusions?):
- जब हम संभावनाओं का उपयोग करते हैं तो हम वास्तव में समझते हैं कि हम क्या कर रहे हैं।यह दूसरे निबंध को प्रेरित करेगा,जो प्रायिकता के सिद्धांत की आलोचना करता है.
- उपर्युक्त आर्टिकल में प्रायिकता:एक दार्शनिक परिप्रेक्ष्य (Probability Philosophical Perspective) के बारे में बताया गया है.
Probability Philosophical Perspective
प्रायिकता:एक दार्शनिक परिप्रेक्ष्य
(Probability Philosophical Perspective)
Probability Philosophical Perspective
प्रायिकता:एक दार्शनिक परिप्रेक्ष्य (Probability Philosophical Perspective) के इस आर्टिकल में बताया गया है कि
प्रायिकता हमें संभावित दुनिया के बारे में बताती है।जीवन में हमारे साथ घटित होनेवाली घटनाओं के परिणाम
Probability Philosophical Perspective
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |