Inclusion-Exclusion Principle
1.आविष्टि-अपवर्जन सिद्धान्त (Inclusion-Exclusion Principle )-
- आविष्टि-अपवर्जन सिद्धान्त (Inclusion-Exclusion Principle ) का उपयोग संयुक्त समुच्चयों की समस्याओं को हल करने में किया जाता है।यदि समुच्चय असंयुक्त है तब इन असंयुक्त समुच्चयों के संघ में उपस्थित अवयवों की गणना,योग नियम (Sum rule) द्वारा आसानी से की जा सकती है।
- परन्तु यदि समुच्चय असंयुक्त नहीं है तो योग नियम में कुछ संशोधन करने पर जिस नियम की उत्पत्ति होती है उसे आविष्टि-अपवर्जन सिद्धान्त (Inclusion-Exclusion Principle ) कहते हैं।
(1.)विविक्त गणित में आविष्टि-अपवर्जन सिद्धान्त (Principle of Inclusion and Exclusion in Discrete Mathematics),आप आविष्टि/अपवर्जन सिद्धांत का उपयोग कैसे करते हैं? (How do you use inclusion/exclusion principle?)-
- आविष्टि और अपवर्जन (पीआईई) का सिद्धांत (Inclusion-Exclusion Principle )
एक गिनती तकनीक है जो अवयवों की संख्या की गणना करता है जो कम से कम कई गुणधर्मों में से एक को संतुष्ट करते हैं, जबकि एक से अधिक गुणधर्म को संतुष्ट करने वाले अवयवों को दो बार नहीं गिना जाता है।
प्रमेय (Theorem):1. यदि A तथा B दो परिमित समुच्चय हैं,तब
\left| A\cup B \right| =\left| A \right| +\left| B \right| -\left| A\cap B \right|
(If A and B are finite sets,then \left| A\cup B \right| =\left| A \right| +\left| B \right| -\left| A\cap B \right| .)
उपपत्ति (Proof):यदि A और B कोई दो समुच्चय हैं तो हम जानते हैं कि
A\cup B=(A\cap { B }^{ \prime })\cup (A\cap B)\cup ({ A }^{ \prime }\cap B) जहां A\cap { B }^{ \prime },A\cap B और { A }^{ \prime }\cap B परस्पर असंयुक्त हैं।
अतः योग नियम से-
\left| A\cup B \right| =\left| A\cap { B }^{ \prime } \right| +\left| A\cap B \right| +\left| { A }^{ \prime }\cap B \right| ...(1)
पुनः A=(A\cap { B }^{ \prime })\cup (A\cap B)\\ \therefore \left| A \right| =\left| A\cap { B }^{ \prime } \right| +\left| A\cap B \right| .....(2)
इसी प्रकार चूंकि
B=(A\cap B)\cup ({ A }^{ \prime } \cap B )\\ \therefore \left| B \right| =\left| A\cap B \right| +\left| { A }^{ \prime }\cap B \right| ...(3)
(2) तथा (3) से-
\left| A \right| +\left| B \right| =\left| A\cap { B }^{ \prime } \right| +\left| A\cap B \right| +\left| A\cap B \right| +\left| { A }^{ \prime }\cap B \right|
या \left| A \right| +\left| B \right| -\left| A\cap B \right| =\left| A\cap { B }^{ \prime } \right| +\left| A\cap B \right| +\left| { A }^{ \prime }\cap B \right| ...(4)
(1) तथा (4) से स्पष्ट है कि
\left| A\cup B \right| =\left| A \right| +\left| B \right| -\left| A\cap B \right|
प्रमेय (Theorem):2.यदि A ,B तथा C तीन परिमित समुच्चय हैं।तब (If A,B and C are three finite sets then)
\left| A\cup B\cup C \right| =\left| A \right| +\left| B \right| +\left| C \right| -\left| A\cap B \right| -\left| A\cap C \right| -\left| B\cap C \right| +\left| A\cap B\cap C \right|
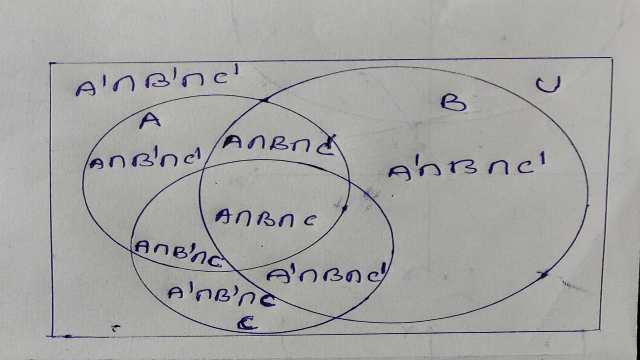
उपपत्ति (Proof):माना A,B और C तीन परिमित समुच्चय हैं।तब इन्हें असंयुक्त उप समुच्चयों के रूप में निम्न प्रकार से व्यक्त किया जा सकता है:
A=(A\cap { B }^{ \prime }\cap { C }^{ \prime })\cup (A\cap { B }\cap { C }^{ \prime })\cup (A\cap { B }^{ \prime }\cap { C })\cup (A\cap { B }\cap { C })\\ B=({ A }^{ \prime }\cap { B }\cap { C }^{ \prime })\cup (A\cap { B }\cap { C }^{ \prime })\cup ({ A }^{ \prime }\cap { B }\cap { C })\cup (A\cap { B }\cap { C })
तथा C=({ A }^{ \prime }\cap { { B }^{ \prime } }\cap { C })\cup (A\cap { { B }^{ \prime } }\cap { C })\cup ({ A }^{ \prime }\cap { B }\cap { C })\cup (A\cap { B }\cap { C })
चूंकि उपर्युक्त सभी समुच्चय { A }\cap { { B }^{ \prime } }\cap { C }^{ \prime },{ A }\cap { { B } }\cap { C }^{ \prime },{ A }\cap { { B }^{ \prime } }\cap { C } इत्यादि परस्पर असंयुक्त हैं, अतः योग नियम से-
\left| A \right| =\left| A\cap { B }^{ \prime }\cap { C }^{ \prime } \right| +\left| A\cap { B }\cap { C }^{ \prime } \right| +\left| A\cap { B }^{ \prime }\cap { C } \right| +\left| A\cap { B }\cap { C } \right| \\ \left| B \right| =\left| { A }^{ \prime }\cap { B }\cap { C }^{ \prime } \right| +\left| A\cap { B }\cap { C }^{ \prime } \right| +\left| { A }^{ \prime }\cap { B }\cap { C } \right| +\left| A\cap { B }\cap { C } \right|
तथा \left| C \right| =\left| { A }^{ \prime }\cap { { B }^{ \prime } }\cap { C } \right| +\left| A\cap { { B }^{ \prime } }\cap { C } \right| +\left| { A }^{ \prime }\cap { B }\cap { C } \right| +\left| A\cap { B }\cap { C } \right|
\left| A \right| +\left| B \right| +\left| C \right| =[\left| A\cap { B }^{ \prime }\cap { C }^{ \prime } \right| +\left| A\cap { B }\cap { C }^{ \prime } \right| +\left| A\cap { B }^{ \prime }\cap { C } \right| +\left| A\cap { B }\cap { C } \right| +\left| { A }^{ \prime }\cap { B }\cap { C }^{ \prime } \right| +\left| A\cap { B }\cap { C }^{ \prime } \right| +\left| { A }^{ \prime }\cap { B }\cap { C } \right| +\left| A\cap { B }\cap { C } \right| +\left| { A }^{ \prime }\cap { { B }^{ \prime } }\cap { C } \right| +\left| A\cap { { B }^{ \prime } }\cap { C } \right| +\left| { A }^{ \prime }\cap { B }\cap { C } \right| +\left| A\cap { B }\cap { C } \right|]- \left| A\cap { B }\cap { C } \right| \\ =\left| A\cup B\cup C \right| +\left| A\cap B \right| +\left| A\cap C \right| +\left| B\cap C \right| -\left| A\cap B\cap C \right|
या \left| A\cup B\cup C \right| =\left| A \right| +\left| B \right| +\left| C \right| -\left| A\cap B \right| -\left| A\cap C \right| -\left| B\cap C \right| +\left| A\cap B\cap C \right|
(2.)आविष्टि-अपवर्जन सिद्धांत: आगमन द्वारा प्रमाण (Inclusion-Exclusion Principle: proof by Induction)-
प्रमेय (Theorem):3.यदि { A }_{ 1 },{ A }_{ 2 },.....,{ A }_{ n } ,n परिमित समुच्चय हैं,तब
(If { A }_{ 1 },{ A }_{ 2 },.....,{ A }_{ n } are n finite sets,then)
\left| { A }_{ 1 }\cup { A }_{ 2 }\cup .....\cup { A }_{ n } \right| =\overset { n }{ \underset { i=1 }{ \Sigma } } \left| { A }_{ i } \right| -\overset { n }{ \underset { 1\le i<j }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ j } \right| +\overset { n }{ \underset { 1\le i<j<k }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ j }\cap { A }_{ k } \right| +....+{ (-1) }^{ n-1 }\left| { A }_{ 1 }\cap { A }_{ 2 }\cap .....\cap { A }_{ n } \right|
जहां द्वितीय योगफल पूर्णांकों {1,2,3,……,n} के सभी 2-संचयों {I,j}, तृतीय योगफल {1,2,3,……,n} के सभी 3-संचयों {I,j,k} इत्यादि-इत्यादि पर लिए गए हैं।
(Where the second summation is taken over all 2-combinations {I,j} of the integers {1,2,3,…..,n} , the third summation is taken over all 3-combinations {I,j,k} of {1,2,3,…..,n} and so on.)
उपपत्ति (Proof):प्रमेय को हम गणितीय आगमन सिद्धान्त (Principle of mathematical induction) से सिद्ध करेंगे।
n=1 के लिए प्रमेय स्वाभाविक रूप से सत्य है जबकि n=2 तथा 3 के लिए पूर्व में सिद्ध कर चुके हैं।
अतः माना कि प्रमेय m समुच्चयों { A }_{ 1 },{ A }_{ 2 },.....,{ A }_{ m } के लिए सत्य है,I.e. माना कि,
\left| { A }_{ 1 }\cup { A }_{ 2 }\cup .....\cup { A }_{ m } \right| =\overset { m }{ \underset { i=1 }{ \Sigma } } \left| { A }_{ i } \right| -\overset { m }{ \underset { 1\le i<j }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ j } \right| +\overset { m }{ \underset { 1\le i<j<k }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ j }\cap { A }_{ k } \right| +....+{ (-1) }^{ m-1 }\left| { A }_{ 1 }\cap { A }_{ 2 }\cap .....\cap { A }_{ m } \right| ...(1)
तब m+1 समुच्चयों { A }_{ 1 },{ A }_{ 2 },.....,{ A }_{ m+1 } के लिए
\left| { A }_{ 1 }\cup { A }_{ 2 }\cup .....\cup { A }_{ m }\cup { A }_{ m+1 } \right| =\left| { (A }_{ 1 }\cup { A }_{ 2 }\cup .....\cup { A }_{ m })\cup { A }_{ m+1 } \right| =\left| { A }_{ 1 }\cup { A }_{ 2 }\cup .....\cup { A }_{ m } \right| +\left| { A }_{ m+1 } \right| -\left| { (A }_{ 1 }\cup { A }_{ 2 }\cup .....\cup { A }_{ m })\cap { A }_{ m+1 } \right|
[दो समुच्चयों के लिए प्रमेय का प्रयोग करने पर]
परन्तु \left| { (A }_{ 1 }\cup { A }_{ 2 }\cup .....\cup { A }_{ m })\cap { A }_{ m+1 } \right| =\left| { (A }_{ 1 }\cap { A }_{ m+1 })\cup ({ A }_{ 2 }\cap { A }_{ m+1 })\cup ....\cup ({ A }_{ m }\cap { A }_{ m+1 } \right| ....(2)
अतः (2) का दक्षिण पक्ष है:
\left| { A }_{ 1 }\cup { A }_{ 2 }\cup .....\cup { A }_{ m } \right| +\left| { A }_{ m+1 } \right| -\left| { (A }_{ 1 }\cap { A }_{ m+1 })\cup ({ A }_{ 2 }\cap { A }_{ m+1 })\cup ....\cup ({ A }_{ m }\cap { A }_{ m+1 } \right| =\\ \overset { m }{ \underset { i=1 }{ \Sigma } } \left| { A }_{ i } \right| -\overset { m }{ \underset { 1\le i<j }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ j } \right| +\overset { m }{ \underset { 1\le i<j<k }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ j }\cap { A }_{ k } \right| +....+{ (-1) }^{ m-1 }\left| { (A }_{ 1 }\cap { A }_{ 2 }\cap .....\cap { A }_{ m } \right| +\left| { A }_{ m+1 } \right| \\ -\{ \overset { m }{ \underset { i=1 }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ m+1 } \right| -\overset { m }{ \underset { 1\le i<j }{ \Sigma } } \left| ({ A }_{ i }\cap { A }_{ m+1 })\cap { (A }_{ j }\cap { A }_{ m+1 }) \right| +\overset { m }{ \underset { 1\le i<j<k }{ \Sigma } } \left| ({ A }_{ i }\cap { A }_{ m+1 })\cap ({ A }_{ j }\cap { A }_{ m+1 })\cap ({ A }_{ m }\cap { A }_{ m+1 } \right| +....+{ (-1) }^{ m-1 }\left| { (A }_{ i }\cap { A }_{ m+1 })\cap ({ A }_{ j }\cap { A }_{ m+1 })\cap ....\cap ({ A }_{ m }\cap { A }_{ m+1 } \right| \\ \}\\ =\overset { m+1 }{ \underset { i=1 }{ \Sigma } } \left| { A }_{ i } \right| -\{ \overset { m }{ \underset { 1\le i<j }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ j } \right| +\overset { m }{ \underset { 1\le i<j }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ j }\cap { A }_{ m+1 } \right| \} +\{ \overset { m }{ \underset { 1\le i<j<k }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ j }\cap { A }_{ k } \right| +\overset { m }{ \underset { 1\le i<j<k }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ j }\cap { A }_{ k }\cap { A }_{ m+1 } \right| \} +......+{ (-1) }^{ m-1 }\{ \left| { (A }_{ 1 }\cap { A }_{ 2 }\cap .....\cap { A }_{ m } \right| +\left| { (A }_{ 1 }\cap { A }_{ 2 }\cap .....\cap { A }_{ m }\cap { A }_{ m+1 } \right| \\ \} \\ =\overset { m+1 }{ \underset { i=1 }{ \Sigma } } \left| { A }_{ i } \right| -\overset { m+1 }{ \underset { 1\le i<j }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ j } \right| +\overset { m }{ \underset { 1\le i<j<k }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ j }\cap { A }_{ k } \right| +...+{ (-1) }^{ m }\{ \left| { (A }_{ 1 }\cap { A }_{ 2 }\cap .....\cap { A }_{ m } \right|
(2) है
\left| { A }_{ 1 }\cup { A }_{ 2 }\cup .....\cup { A }_{ m+1 } \right| =\overset { m+1 }{ \underset { i=1 }{ \Sigma } } \left| { A }_{ i } \right| -\overset { m }{ \underset { 1\le i<j }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ j } \right| +\overset { m+1 }{ \underset { 1\le i<j<k }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ j }\cap { A }_{ k } \right| +...+{ (-1) }^{ m }\{ \left| { (A }_{ 1 }\cap { A }_{ 2 }\cap .....\cap { A }_{ m+1 } \right|
अतः प्रमेय (m+1) समुच्चयों के लिए भी सत्य है।
अतः प्रमेय सभी धनात्मक पूर्णांकों n के लिए सत्य है।
\left| { A }_{ 1 }\cup { A }_{ 2 }\cup .....\cup { A }_{ n } \right| =\overset { n }{ \underset { i=1 }{ \Sigma } } \left| { A }_{ i } \right| -\overset { n }{ \underset { 1\le i<j }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ j } \right| +\overset { n }{ \underset { 1\le i<j<k }{ \Sigma } } \left| { A }_{ i }\cap { A }_{ j }\cap { A }_{ k } \right| +....+{ (-1) }^{ n-1 }\left| { A }_{ 1 }\cap { A }_{ 2 }\cap .....\cap { A }_{ n } \right|
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Generating Functions
Example-1.1 से 250 के मध्य उन पूर्णांकों की संख्या ज्ञात कीजिए जो 2,3,5 तथा 7 में से किसी भी पूर्णांक से विभाजित होते हैं।
(Determine the number of integers between 1 and 250 ,that are divisible by any of the integers 2,3,5 and 7.)
Solution- माना S उन सभी पूर्णांकों x का समुच्चय है जहां 1\leq x\leq 250 माना { A }_{ 1 },{ A }_{ 2 },{ A }_{ 3 } तथा { A }_{ 4 } समुच्चय के उन अवयवों जो क्रमशः 2,3,5 तथा 7 से विभाजित किए जा सकते हैं।तब { A }_{ 1 } \cap { A }_{ 2 }, s के उन पूर्णांकों का समुच्चय है जो ,6 से विभाजित होते हैं।
अब \left | { A }_{ 1 } \right |=\frac{250}{2}=125 \\ \left | { A }_{ 2 } \right |=\frac{250}{3}=83[[x] का अर्थ महतम पूर्णाक है \leq x]
\left | { A }_{ 3 } \right |=\frac{250}{5}=125,\left | { A }_{ 4 } \right |=\frac{250}{7}=35 \\ \left | { A }_{ 1 } \cap { A }_{ 2 } \right |=\frac{250}{6}=41 ,\left | { A }_{ 1 } \cap { A }_{ 3 } \right |=\frac{250}{10}=25 \\ \left | { A }_{ 1 } \cap { A }_{ 4 } \right |=\frac{250}{14}=17 , \left | { A }_{ 2 } \cap { A }_{ 3 } \right |=\frac{250}{15}=16 \\ \left | { A }_{ 2 } \cap { A }_{ 4 } \right |=\frac{250}{21}=11 \\ \left | { A }_{ 3 } \cap { A }_{ 4 } \right |=\frac{250}{35}=7 \\ \left | { A }_{ 1 } \cap { A }_{ 2 } \cap { A }_{ 3 } \right |=\frac{250}{30}=8 \\ \left | { A }_{ 1 } \cap { A }_{ 2 } \cap { A }_{ 4 } \right |=\frac{250}{42}=5 \\ \left | { A }_{ 1 } \cap { A }_{ 3 } \cap { A }_{ 4 } \right |=\frac{250}{70}=3 \\ \left | { A }_{ 1 } \cap { A }_{ 3 } \cap { A }_{ 4 } \right |=\frac{250}{105}=2
तथा \left | { A }_{ 1 } \cap { A }_{ 2 } \cap { A }_{ 3 } \cap { A }_{ 4 } \right |=\frac{250}{210}=1
तब \left| { A }_{ 1 }\cup { A }_{ 2 }\cup { A }_{ 3 }\cup { A }_{ 4 } \right| = \left| { A }_{ 1 } \right|+ \left| { A }_{ 2 } \right|+ \left| { A }_{ 3 } \right|+ \left| { A }_{ 4 } \right| -\left| { A }_{ 1 }\cap { A }_{ 2 } \right|-\left| { A }_{ 1 }\cap { A }_{ 3 } \right|-\left| { A }_{ 1 }\cap { A }_{ 4 } \right|-\left| { A }_{ 2 }\cap { A }_{ 3 } \right|-\left| { A }_{ 2 }\cap { A }_{ 4 } \right|-\left| { A }_{ 3 }\cap { A }_{ 4 } \right|+\left| { A }_{ 1 }\cap { A }_{ 2 }\cap { A }_{ 3 } \right|+\left| { A }_{ 1 }\cap { A }_{ 2 }\cap { A }_{ 4 } \right|+\left| { A }_{ 1 }\cap { A }_{ 3 }\cap { A }_{ 4 } \right|+\left| { A }_{ 2 }\cap { A }_{ 3 }\cap { A }_{ 4 }\right|-\left| { A }_{ 1 }\cap { A }_{ 2 }\cap { A }_{ 3 }\cap { A }_{ 4 }\right|
=125+83+50+35-41-25-17-16-11-7+8+5+3+2-1
=293-117+18-1
=311-117=193
उपर्युक्त उदाहरण के द्वारा आविष्टि-अपवर्जन सिद्धान्त (Inclusion-Exclusion Principle ) को समझ सकते हैं।
Example-2.किसी महाविद्यालय में 42 विद्यार्थी अर्थशास्त्र;45 विद्यार्थी दर्शनशास्र;65 विद्यार्थी भूगोल ;20 विद्यार्थी अर्थशास्त्र एवं भूगोल;15 विद्यार्थी भूगोल एवं दर्शनशास्र;25 विद्यार्थी अर्थशास्त्र एवं दर्शनशास्र तथा 8 विद्यार्थी तीनों विषय पढ़ते हैं।अर्थशास्त्र,भूगोल तथा दर्शनशास्र में से कम से कम एक विषय पढ़ने वाले विद्यार्थियों की संख्या ज्ञात कीजिए।
(In a college,42 students study Economics,45 students study Philosophy;65 study Geography;20 students study Economics and Geography;15 study Geography and Philosophy;25 study Economics and Philosophy and 8 students study all the three subjects.Determine the number of students studying at least one of these three subjects.)
Solution:-माना कि E,Pतथा G क्रमशः अर्थशास्त्र, दर्शनशास्र तथा भूगोल पढ़ने वाले विद्यार्थियों का समुच्चय है।
|E|=42,|P|=45,|G|=65
\left| E\cap P \right|=20,\left| P\cap G \right|=15,\left| E\cap G \right|=25 \\ \left| E\cap P \cap G \right|=8 \\ \left| E\cup P \cup G \right|=\left| E \right|+\left| P \right|+\left| G \right|-\left| E\cap P \right|- \left| P\cap G \right|-\left| E\cap G \right|+\left| E\cap P \cap G \right|
=42+45+65-20-15-25+8
=160-60
\left| E\cup P \cup G \right|=100
अतः कम से कम एक विषय पढ़ने वाले विधार्थी =100
उपर्युक्त उदाहरण के द्वारा आविष्टि-अपवर्जन सिद्धान्त (Inclusion-Exclusion Principle ) को समझ सकते हैं।
Example-3.किसी कक्षा में 175 विद्यार्थी हैं। जिनमें से 100 विद्यार्थी गणित;70 विद्यार्थी भौतिकी;46 विद्यार्थी रसायनशास्त्र;30 विद्यार्थी गणित और भौतिकी;28 विद्यार्थी गणित और रसायनशास्त्र;23 विद्यार्थी भौतिकी तथा रसायनशास्त्र एवं 18 विद्यार्थी तीनों विषय पढ़ते हैं।केवल गणित, भौतिकी तथा रसायनशास्त्र पढने वाले विद्यार्थियों की संख्या ज्ञात कीजिए।ऐसे कितने विद्यार्थी हैं जो उपर्युक्त में से कोई भी विषय नहीं पढ़ते?
(In a class of 175 students 100 students As study Mathematics;70 study Physics;46 study Chemistry;30 students study Mathematics and Physics;28 study Mathematics and Chemistry;23 study Physics and Chemistry and 18 students all the three subjects.Determine the number of students studying only one subject Mathematics,Physics and Chemistry.How many students do not study any of these three subjects.)
Solution-माना कि M,P तथा C क्रमशः गणित, भौतिकी तथा रसायनशास्त्र पढ़ने वाले विद्यार्थियों का समुच्चय है।
अतः |M|=42,|P|=45,|C|=65
अतः \left| M\cap P \right|=30,\left| M\cap C \right|=28,\left| P\cap C \right|=23 \\ \left| M\cap P \cap C \right|=18 \\ \left| M\cup P \cup C \right|=\left| M \right|+\left| P \right|+\left| C \right|-\left| M\cap P \right|- \left| M\cap C \right|-\left| P\cap C \right|+\left| M\cap P \cap C \right|
=100+70+46-30-28-23+18
=216+18-81
=234-81
=153
अतः कोई भी विषय न पढ़ने वाले विद्यार्थियों की संख्या=175-153=22
केवल गणित विषय पढ़ने वाले विद्यार्थियों की संख्या=
\left| M \cup P' \cup C' \right|=\left| M \right|-\left| M\cap P \right|- \left| M\cap C \right|+\left| M\cap P \cap C \right|
=100-30-28+18
\left| M \cup P' \cup C' \right|=118-58=60
केवल भौतिकी पढ़ने वाले विद्यार्थियों की संख्या=
\left| M' \cup P \cup C' \right|=\left| P \right|-\left| M\cap P \right|- \left| P\cap C \right|+\left| M\cap P \cap C \right|
=70-30-23+18
=88-53
=35
केवल रसायनशास्त्र पढ़ने वाले विद्यार्थियों की संख्या=
\left| M' \cup P' \cup C \right|=\left| C \right|-\left| M\cap C \right|- \left| P\cap C \right|+\left| M\cap P \cap C \right|
=46-28-23+18
=64-51
=13
उपर्युक्त उदाहरण के द्वारा आविष्टि-अपवर्जन सिद्धान्त (Inclusion-Exclusion Principle ) को समझ सकते हैं।
Example-4.42विद्यार्थियों की एक कक्षा में प्रत्येक विद्यार्थी क्रिकेट,हाॅकी तथा फुटबाल में से कम से कम एक खेल अवश्य खेलता है।कुल 14 विद्यार्थी क्रिकेट,20 विद्यार्थी हाॅकी तथा 24 विद्यार्थी फुटबॉल खेलते हैं।3 विद्यार्थी क्रिकेट और फुटबॉल;2विद्यार्थी हाॅकी तथा फुटबाल खेलते हैं जबकि कोई भी विद्यार्थी तीनों खेल नहीं खेलता।उन विद्यार्थियों की संख्या ज्ञात कीजिए जो क्रिकेट खेलते हैं परन्तु हाॅकी नहीं।
(In a class of 42 students each students plays at least one of the three games Cricket, Hockey and Football.It were found that 14 students play Cricket.20 play Hockey and 24 students play Football.3 students play both Cricket and Football;2 students play both Hockey and Football but none play all the three games.Determine the number of students who play Cricket but not Hockey.)
Solution-माना कि C,Hतथा F क्रमशः क्रिकेट, हाॅकी तथा फुटबाल खेलते वाले विद्यार्थियों का समुच्चय है।
अतः \left| C\cup F \right|+\left| C\cup H \cap F \right|=42 \\|C|=14,|H|=20,|F|=24 \\ \left| C\cap F \right|=3,\left| H\cap F \right|=2 , \left| C\cap H \cap F \right|=0
अतः \left| C\cup H \cup F \right|=\left| C \right|+\left| H \right|+\left| F \right|-\left| C\cap H \right|- \left| H\cap F \right|-\left| C\cap F \right|+\left| C\cap H \cap F \right| \\ \Rightarrow 42=14+20+24-\left| C\cap H \right|-2-3+0 \\ \Rightarrow 42=58-\left| C\cap H \right|-5 \\ \Rightarrow 42=53-\left| C\cap H \right| \\ \Rightarrow \left| C\cap H \right|=53-42 \\ \Rightarrow \left| C\cap H \right|=11
अतः क्रिकेट खेलनेवालों परन्तु हाॅकी नहीं खेलने वाले विद्यार्थियों की संख्या=
\left| C\cap H' \right| \\ =\left| C \right| - \left| C\cap H' \right| \\ =14-11 \\ \left| C\cap H' \right| =3
उपर्युक्त उदाहरणों के द्वारा आविष्टि-अपवर्जन सिद्धान्त (Inclusion-Exclusion Principle ) को समझ सकते हैं।
3.आविष्टि-अपवर्जन सिद्धान्त अभ्यास (Inclusion-Exclusion Principle Exercise)-
(1.)90 विद्यार्थियों के एक समूह में जिसमें प्रत्येक विद्यार्थी के पास कम से कम गणित,कम्प्यूटर विज्ञान या सांख्यिकी का विषय है,यह पाया गया कि 40 विद्यार्थियों के पास गणित,50 विद्यार्थियों के पास कम्प्यूटर विज्ञान तथा 60 विद्यार्थियों के पास सांख्यिकी विषय है।10 विद्यार्थियों के पास गणित तथा कम्प्यूटर विज्ञान,40 के पास गणित तथा सांख्यिकी तथा 10 विद्यार्थियों के पास सभी तीन विषय है।उन विद्यार्थियों की संख्या ज्ञात कीजिए जिनके पास कम्प्यूटर विज्ञान तथा सांख्यिकी विषय है परन्तु गणित नहीं है।
(In a group Mathematics or Computer science or Statistics,it were found 40 students having Mathematics,50 students having Computer science and 60 students having Statistics.10 students have Mathematics as well as Computer science,40 students have Mathematics as well as Statistics and 10 students have all the three subjects.Find the number of students who have Computer science and Statistics but not Mathematics.)
(2.) चेन्नई में किसी काॅलेज के विद्यार्थियों का भाषा सर्वेक्षण करने पर पाया गया कि 900 विद्यार्थी अंग्रेजी,1200 विद्यार्थी तमिल तथा 750 विद्यार्थी हिन्दी जानते हैं।450 विद्यार्थी अंग्रेजी तथा तमिल,300 विद्यार्थी अंग्रेजी तथा हिंदी और 200 विद्यार्थी तमिल और हिन्दी का ज्ञान रखते हैं।150 विद्यार्थी तीनों भाषाओं को जानते हैं।बताइए कि कितने विद्यार्थी
(i)केवल हिन्दी
(ii)कम से कम एक भाषा
(iii) अंग्रेजी तथा एक अन्य भाषा तमिल और हिन्दी में से केवल एक परन्तु दोनों नहीं
(iv)कम से कम दो भाषाएं जानते हैं।
(In a language survey of students of a college in Chennai,it was found that 900 students know English,1200 students know Tamil,750 students know Hindi.450 students know English and Tamil.300 students know English and Hindi while 200 students know Tamil and Hindi.150 students know all the three language.Find howmany students know:
(i) Hindi only
(ii)at least one language
(iii) English and one but not both of Tamil and Hindi
(iv)at least two language
(3.)1 तथा 1000 के मध्य ऐसे कितने पूर्णांक हैं जो 2,3,5 अथवा 7 से विभाजित नहीं होते?
(1 and 1000 which are not divisible by 2,3,5 and 7?)
(4.) कितने प्रकार से अंग्रेजी वर्णमाला के अक्षरों AAAA EEE OO को इस प्रकार विन्यासित किया जा सकता है कि एक ही प्रकार के सभी वर्ण एक खण्ड के रूप में उपस्थित न हों।
(In how many ways the letters AAAA EEE OO of English alphabet can be arranged so that all letters of the same kind do not appear in a single block?)
(5.)कितने प्रकार से अंग्रेजी वर्णमाला के 26 वर्णों को विन्यसित किया जा सकता है कि SUN,TEA,BOY या GIRL में से कोई भी शब्द न प्राप्त हो?
(In how many ways the 26 letters of the English alphabet can be permuted so that none of the word SUN,BOY or GIRL occurs?)
उपर्युक्त सवालों को हल करने पर आविष्टि-अपवर्जन सिद्धान्त (Inclusion-Exclusion Principle ) को ठीक प्रकार से समझा जा सकता है।
उत्तर (Answer)-
(1)\left| M'\cap C\cap S \right|=10 \\ (2)(i)\left| H \right|-\left| P\cup Q \right|=400 (ii)\left| E\cap T\cup H \right|=2050 (iii)\left| P \right|+\left| R \right| -2\left| P \cap R \right|=450 (iv)\left| P\cup Q \cup R\right|=650 \\(3)\left | { A }_{ 1 }' \cap { A }_{ 2 }'\cap { A }_{ 3 }' \cap { A }_{ 4 }' \right |=228 \\ (4)N( A'\cap E'\cap Q' )=\frac{9!}{4!3!2!}-[\frac{6!}{3!2!}+\frac{7!}{4!2!}+\frac{8!}{4!3!}]+[\frac{4!}{2!}+\frac{5!}{3!}+\frac{6!}{4!}]-3! \\ (5)\left| B'\cap C' \cap D' \cap E' \right|=26!-3×24!-23!+3×22!+3×21!-20!-3×19!+17!
4.विविक्त गणित में समावेशन अपवर्जन सिद्धांत क्या है? (What is inclusion exclusion principle in discrete maths?)-
- समावेशन-अपवर्जन सिद्धांत कहता है कि किसी भी संख्या में परिमित सेटों के लिए।सेटों का योग द्वारा दिया जाता है
= सभी एकल सेटों के आकार के योग - सभी 2-सेट प्रतिच्छेदों का योग + सभी 3-सेट प्रतिच्छेदों का योग - सभी 4-सेटों के प्रतिच्छेदों का योग
5.4 सेटो का समावेशन-आपवर्जन सिद्धान्त (Inclusion-Exclusion Principle 4 sets)-
- |A∪B∪C∪D|=|A|+|B|+|C|+|D|} all singletons−(|A∩B|+|A∩C|+|A∩D|+|B∩C|+|B∩D|+|C∩D|)} all pairs+(|A∩B∩C|+|A∩B∩D|+|A∩C∩D|+|B∩C∩D|)} all triples−|A∩B∩C∩D|} all quadruples
Also Read This Article:-Mathematical Induction
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |