convert integral to polar coordinates
1.समाकल को ध्रुवीय निर्देशांक में परिवर्तित करें,द्वि-समाकलन का कार्तीय से ध्रुवीय निर्देशांकों में परिवर्तन (convert integral to polar coordinates,Change of double integral from Cartesian to polar coordinates)-
समाकल को ध्रुवीय निर्देशांक में परिवर्तित करें,द्वि-समाकलन का कार्तीय निर्देशांकों में परिवर्तन (convert integral to polar coordinates,Change of double integral from Cartesian to polar coordinates) करने पर कई बार द्वि-समाकल का मान सरलता से ज्ञात किया जा सकता है।इसके लिए
x=rcos\theta ,y=rsin\theta तथा dA=dxdy=rd\theta dr
प्रतिस्थापन का प्रयोग करने पर
\int { \int _{ A }^{ \quad }{ f\left( x,y \right) dxdy } } =\int { \int _{ A }^{ \quad }{ f\left( rcos\theta ,rsin\theta \right) rd\theta dr } }
r व \theta के लिए समाकलन की सीमाएं समाकलन क्षेत्र से निर्धारित की जाती है।इसके लिए पहले कार्तीय समाकलन की सीमाओं से समाकलन का क्षेत्र (region) ज्ञात करते हैं तथा फिर इसके पश्चात् ध्रुवीय समाकल की सीमाएं ज्ञात करते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Double Integral in Polar Coordinates
2.समाकल को ध्रुवीय निर्देशांक में परिवर्तित करें,द्वि-समाकलन का कार्तीय से ध्रुवीय निर्देशांकों में परिवर्तन (convert integral to polar coordinates,Change of double integral from Cartesian to polar coordinates)पर आधारित उदाहरण,ध्रुवीय निर्देशांक में द्वि-समाकल उदाहरण हैं (double integrals in polar coordinates examples)-
निम्नलिखित समाकलों को ध्रुवीय निर्देशांकों में परिवर्तित कर मान ज्ञात कीजिए-
(Evaluate the following integrals by changing to polar coordinates)
Example-1.\int _{ 0 }^{ 1 }{ \int _{ 0 }^{ x }{ \frac { { x }^{ 3 }dxdy }{ \sqrt { { x }^{ 2 }+{ y }^{ 2 } } } } }
Solution-\int _{ 0 }^{ 1 }{ \int _{ 0 }^{ x }{ \frac { { x }^{ 3 }dxdy }{ \sqrt { { x }^{ 2 }+{ y }^{ 2 } } } } }
ध्रुवीय निर्देशांकों में परिवर्तित करने पर-
x=0,x=1,y=0,y=r\\ x=rcos\theta ,y=rsin\theta \\ y=x\\ rcos\theta =rsin\theta \\ tan\theta =1\\ \theta =\frac { \pi }{ 4 }
y=0 से
rsin\theta =0\\ \theta =0
x=0 से
rcos\theta =0\\ r=0
r=0
x=1 से
rcos\theta =1\\ r=\sec { \theta } \\ \int _{ 0 }^{ 1 }{ \int _{ 0 }^{ x }{ \frac { { x }^{ 3 }dxdy }{ \sqrt { { x }^{ 2 }+{ y }^{ 2 } } } } } =\int _{ 0 }^{ \frac { \pi }{ 4 } }{ \int _{ 0 }^{ \sec { \theta } }{ \frac { { r }^{ 3 }\cos ^{ 3 }{ \theta } }{ \sqrt { { r }^{ 2 }\cos ^{ 2 }{ \theta } +{ r }^{ 2 }\sin ^{ 2 }{ \theta } } } } } rd\theta dr\\ =\int _{ 0 }^{ \frac { \pi }{ 4 } }{ \int _{ 0 }^{ \sec { \theta } }{ { r }^{ 3 }\cos ^{ 3 }{ \theta } } } drd\theta \\ =\int _{ 0 }^{ \frac { \pi }{ 4 } }{ { \left[ \frac { { r }^{ 4 } }{ 4 } \right] }_{ 0 }^{ \sec { \theta } } } \cos ^{ 3 }{ \theta } d\theta \\ =\frac { 1 }{ 4 } \int _{ 0 }^{ \frac { \pi }{ 4 } }{ { sec }^{ 4 }\theta } \cos ^{ 3 }{ \theta } d\theta \\ =\frac { 1 }{ 4 } \int _{ 0 }^{ \frac { \pi }{ 4 } }{ { sec }\theta } d\theta \\ =\frac { 1 }{ 4 } { \left[ \log { \left| sec\theta +tan\theta \right| } \right] }_{ 0 }^{ \frac { \pi }{ 4 } }\\ =\frac { 1 }{ 4 } \log { \left( sec\frac { \pi }{ 4 } +tan\frac { \pi }{ 4 } \right) } \\ =\frac { 1 }{ 4 } \log { \left( \sqrt { 2 } +1 \right) }
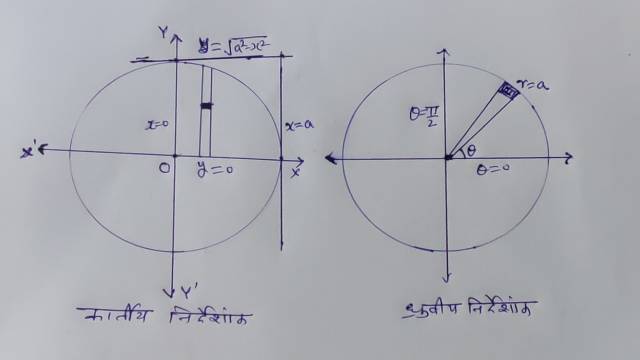
Example-2.\int _{ 0 }^{ a }{ \int _{ 0 }^{ \sqrt { { a }^{ 2 }-{ x }^{ 2 } } }{ { y }^{ 2 } } \sqrt { { x }^{ 2 }+{ y }^{ 2 } } dxdy }
Solution-\int _{ 0 }^{ a }{ \int _{ 0 }^{ \sqrt { { a }^{ 2 }-{ x }^{ 2 } } }{ { y }^{ 2 } } \sqrt { { x }^{ 2 }+{ y }^{ 2 } } dxdy }
ध्रु्वीय निर्देशांकों में परिवर्तित करने पर-
x=0,x=a,y=0,y=\sqrt { { a }^{ 2 }-{ x }^{ 2 } } let\quad { x }^{ 2 }+{ y }^{ 2 }={ a }^{ 2 }\\ x=rcos\theta ,y=rsin\theta
x=0 से
rcos\theta =0\\ r=0,cos\theta =0\Rightarrow \theta =\frac { \pi }{ 2 }
y=0 से
rsin\theta =0\\ \theta =0\\ { x }^{ 2 }+{ y }^{ 2 }={ a }^{ 2 }\\ { r }^{ 2 }\cos ^{ 2 }{ \theta } +{ r }^{ 2 }\sin ^{ 2 }{ \theta } ={ a }^{ 2 }\\ { r }^{ 2 }={ a }^{ 2 }\\ r=a\\ \int _{ 0 }^{ a }{ \int _{ 0 }^{ \sqrt { { a }^{ 2 }-{ x }^{ 2 } } }{ { y }^{ 2 } } \sqrt { { x }^{ 2 }+{ y }^{ 2 } } dxdy } =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \int _{ 0 }^{ a }{ { r }^{ 2 }\sin ^{ 2 }{ \theta } \sqrt { { r }^{ 2 }\cos ^{ 2 }{ \theta } +{ r }^{ 2 }\sin ^{ 2 }{ \theta } } } } rd\theta dr\\ =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \int _{ 0 }^{ a }{ { r }^{ 2 }\sin ^{ 2 }{ \theta } \sqrt { { r }^{ 2 }\cos ^{ 2 }{ \theta } +{ r }^{ 2 }\sin ^{ 2 }{ \theta } } } rd\theta dr } \\ =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \int _{ 0 }^{ a }{ { r }^{ 2 }\sin ^{ 2 }{ \theta } .r } .rd\theta dr } \\ =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \int _{ 0 }^{ a }{ { r }^{ 4 }\sin ^{ 2 }{ \theta } } d\theta dr } \\ =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ { [\frac { { r }^{ 5 } }{ 5 } ] }_{ 0 }^{ a } } \sin ^{ 2 }{ \theta } d\theta \\ =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ { \frac { { a }^{ 5 } }{ 5 } } } \sin ^{ 2 }{ \theta } d\theta \\ =\frac { { a }^{ 5 } }{ 5 } \frac { \Gamma \frac { 0+1 }{ 2 } \Gamma \frac { 2+1 }{ 2 } }{ 2\Gamma \frac { 0+2+2 }{ 2 } } \\ =\frac { { a }^{ 5 } }{ 5 } \frac { \sqrt { \pi } .\frac { 1 }{ 2 } \sqrt { \pi } }{ 2\times 1 } \\ =\frac { { \pi a }^{ 5 } }{ 20 }
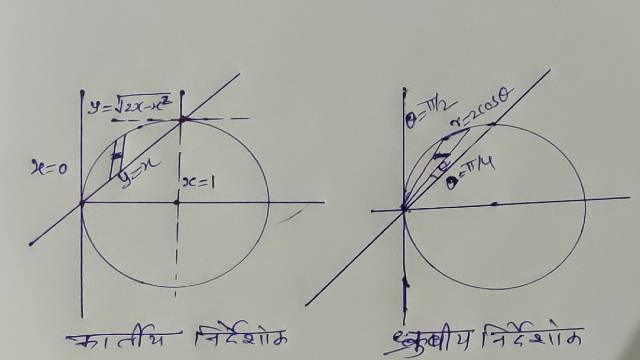
Example-3.\int _{ 0 }^{ 1 }{ \int _{ x }^{ \sqrt { 2x-{ x }^{ 2 } } }{ ({ x }^{ 2 }+y^{ 2 })dxdy } }
Solution–\int _{ 0 }^{ 1 }{ \int _{ x }^{ \sqrt { 2x-{ x }^{ 2 } } }{ ({ x }^{ 2 }+y^{ 2 })dxdy } }
ध्रुवीय निर्देशांकों में परिवर्तित करने पर-
x=0,x=1,y=x,\quad y=\sqrt { 2x-{ x }^{ 2 } } \Rightarrow { x }^{ 2 }+y^{ 2 }-2x=0\\ x=r\cos { \theta } \quad \quad y=rsin\theta \\ { x }^{ 2 }+y^{ 2 }-2x=0 से
\Rightarrow { r }^{ 2 }\cos ^{ 2 }{ \theta } +{ r }^{ 2 }\sin ^{ 2 }{ \theta } -2r\cos { \theta } =0\\ \Rightarrow { r }^{ 2 }-2r\cos { \theta } =0\\ \Rightarrow r(r-2\cos { \theta ) } =0\\ \Rightarrow r=0,r=2\cos { \theta }
y=x से
rsin\theta =rcos\theta \\ \Rightarrow \tan { \theta } =1\\ \tan { \theta } =\tan { \frac { \pi }{ 4 } } \\ \theta =\frac { \pi }{ 4 } \\ x=0\\ rcos\theta =0\\ \theta =\frac { \pi }{ 2 } \\ \int _{ 0 }^{ 1 }{ \int _{ x }^{ \sqrt { 2x-{ x }^{ 2 } } }{ ({ x }^{ 2 }+y^{ 2 })dxdy } } =\int _{ \frac { \pi }{ 4 } }^{ \frac { \pi }{ 2 } }{ \int _{ 0 }^{ 2\cos { \theta } }{ ({ r }^{ 2 }\sin ^{ 2 }{ \theta } +{ r }^{ 2 }\cos ^{ 2 }{ \theta } )rd\theta dr } } \\ =\int _{ \frac { \pi }{ 4 } }^{ \frac { \pi }{ 2 } }{ \int _{ 0 }^{ 2\cos { \theta } }{ { r }^{ 3 }d\theta dr } } \\ =\int _{ \frac { \pi }{ 4 } }^{ \frac { \pi }{ 2 } }{ { [\frac { { r }^{ 4 } }{ 4 } ] }_{ 0 }^{ 2\cos { \theta } }d\theta } \\ =\int _{ \frac { \pi }{ 4 } }^{ \frac { \pi }{ 2 } }{ 4\cos ^{ 4 }{ \theta } d\theta } \\ =4\int _{ \frac { \pi }{ 4 } }^{ \frac { \pi }{ 2 } }{ { (\frac { 1+\cos { 2\theta } }{ 2 } ) }^{ 2 }d\theta } \\ =\int _{ \frac { \pi }{ 4 } }^{ \frac { \pi }{ 2 } }{ { (1+2\cos { 2\theta } +\cos ^{ 2 }{ 2\theta } ) }d\theta } \\ =\int _{ \frac { \pi }{ 4 } }^{ \frac { \pi }{ 2 } }{ 1d\theta } +\int _{ \frac { \pi }{ 4 } }^{ \frac { \pi }{ 2 } }{ 2\cos { 2\theta } d\theta } +\int _{ \frac { \pi }{ 4 } }^{ \frac { \pi }{ 2 } }{ \cos ^{ 2 }{ 2\theta } d\theta } \\ ={ [\theta ] }_{ \frac { \pi }{ 4 } }^{ \frac { \pi }{ 2 } }+{ 2[\sin { 2\theta } ] }_{ \frac { \pi }{ 4 } }^{ \frac { \pi }{ 2 } }+{ [\frac { 1+\cos { 4\theta } }{ 2 } ] }_{ \frac { \pi }{ 4 } }^{ \frac { \pi }{ 2 } }+\frac { 1 }{ 2 } { [\theta ] }_{ \frac { \pi }{ 4 } }^{ \frac { \pi }{ 2 } }+{ [\frac { \sin { 4\theta } }{ 8 } ] }_{ \frac { \pi }{ 4 } }^{ \frac { \pi }{ 2 } }\\ =\frac { \pi }{ 2 } -\frac { \pi }{ 4 } +[\sin { \pi } -\sin { \frac { \pi }{ 2 } } ]+\frac { 1 }{ 2 } [\frac { \pi }{ 2 } -\frac { \pi }{ 4 } ]+\frac { 1 }{ 8 } [\sin { 2\pi } -\sin { \pi } ]\\ =\frac { \pi }{ 4 } -1+\frac { \pi }{ 8 } +0\\ =\frac { 2\pi -8+\pi }{ 8 } \\ =\frac { 3\pi -8 }{ 8 }
Example-4.\int _{ 0 }^{ 2 }{ \int _{ 0 }^{ \sqrt { 2x-{ x }^{ 2 } } }{ \frac { xdxdy }{ \sqrt { { x }^{ 2 }+{ y }^{ 2 } } } } }
Solution-\int _{ 0 }^{ 2 }{ \int _{ 0 }^{ \sqrt { 2x-{ x }^{ 2 } } }{ \frac { xdxdy }{ \sqrt { { x }^{ 2 }+{ y }^{ 2 } } } } }
ध्रुवीय निर्देशांकों में परिवर्तित करने पर-
x=0,x=2,y=0,y=\sqrt { 2x-{ x }^{ 2 } } \\ x=rcos\theta ,y=rsin\theta \\ y=\sqrt { 2x-{ x }^{ 2 } } से
{ x }^{ 2 }+{ y }^{ 2 }-2x=0\\ \Rightarrow { r }^{ 2 }\cos ^{ 2 }{ \theta } +{ r }^{ 2 }\sin ^{ 2 }{ \theta } -2rcos\theta =0\\ \Rightarrow { r }^{ 2 }-2rcos\theta =0\\ \Rightarrow r\left( r-2\cos { \theta } \right) =0\\ \Rightarrow r=0,r=2\cos { \theta }
x=0 से
rcos\theta =0\\ \Rightarrow \theta =\frac { \pi }{ 2 }
y=0 से
\Rightarrow rsin\theta =0\\ \Rightarrow \theta =0\\ \int _{ 0 }^{ 2 }{ \int _{ 0 }^{ \sqrt { 2x-{ x }^{ 2 } } }{ \frac { xdxdy }{ \sqrt { { x }^{ 2 }+{ y }^{ 2 } } } } } =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \int _{ 0 }^{ 2\cos { \theta } }{ \frac { r\cos { \theta } }{ \sqrt { { r }^{ 2 }\cos ^{ 2 }{ \theta } +{ r }^{ 2 }\sin ^{ 2 }{ \theta } } } } } rd\theta dr\\ =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \int _{ 0 }^{ 2\cos { \theta } }{ r\cos { \theta } } } drd\theta \\ =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \cos { \theta } { \left[ \frac { { r }^{ 2 } }{ 2 } \right] }_{ 0 }^{ 2\cos { \theta } }d\theta } \\ =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ 2\cos ^{ 3 }{ \theta } d\theta } \\ =\frac { 2\Gamma \frac { 0+1 }{ 2 } \Gamma \frac { 3+1 }{ 2 } }{ 2\Gamma \frac { 0+3+2 }{ 2 } } \\ =\frac { \sqrt { \pi } .1 }{ \frac { 3 }{ 2 } .\frac { 1 }{ 2 } \sqrt { \pi } } \\ =\frac { 4 }{ 3 }
उपर्युक्त उदाहरणों के द्वारा समाकल को ध्रुवीय निर्देशांक में परिवर्तित करें,द्वि-समाकलन का कार्तीय से ध्रुवीय निर्देशांकों में परिवर्तन (convert integral to polar coordinates,Change of double integral from Cartesian to polar coordinates) को समझा जा सकता है।
3.आप द्वि-समाकलों को ध्रुवीय निर्देशांक में कैसे परिवर्तित करते हैं?,आप ध्रुवीय निर्देशांक में द्वि-समाकल का मूल्यांकन कैसे करते हैं?,द्वि-समाकल को ध्रुवीय समाकल में परिवर्तित करें,ध्रुवीय निर्देशांक मेंं द्वि-समाकल (How do you convert integral to polar coordinates?,How do you evaluate double integrals in polar coordinates?,convert integral to polar coordinates,double integral in polar coordinates)-
फिर से, आयताकार क्षेत्रों पर डबल इंटीग्रल्स पर खंड के रूप में, एक ध्रुवीय आयताकार क्षेत्र पर डबल इंटीग्रल को ध्रुवीय निर्देशांक में पुनरावृत्त समाकल के रूप में व्यक्त किया जा सकता है।अत:, ∬Rf(r,θ)dA=∬Rf(r,θ)rdrdθ=∫θ=βθ=α∫r=br=af(r,θ)rdrdθ. ∬Rf(x,y)dA=∬Rf(rcosθ,rsinθ)rdrdθ
आयताकार निर्देशांक में ∬Df(x,y)dA को ध्रुवीय निर्देशांक में एक द्वि-समाकल में परिवर्तित किया जा सकता है क्योंकि ∬Df(rcos(θ),rsin(θ))rdrdθ.
4.कार्टेशियन और ध्रुवीय निर्देशांक के बीच क्या संबंध है? (What is the relationship between Cartesian and polar coordinates?)-
यह कार्टेशियन निर्देशांक और ध्रुवीय निर्देशांक के बीच एक महत्वपूर्ण अंतर की ओर जाता है।कार्टेशियन निर्देशांक में किसी भी बिंदु के लिए निर्देशांक का एक सेट होता है। ध्रुवीय निर्देशांक के साथ यह सच नहीं है।ध्रुवीय निर्देशांक में वस्तुतः दिए गए बिंदु के लिए निर्देशांक की एक अनंत संख्या है।
इन प्रश्नों के उत्तर द्वारा समाकल को ध्रुवीय निर्देशांक में परिवर्तित करें,द्वि-समाकलन का कार्तीय से ध्रुवीय निर्देशांकों में परिवर्तन (convert integral to polar coordinates,Change of double integral from Cartesian to polar coordinates) को समझने में ओर सरलता होगी।
Also Read This Article:-How to solve double integrals?
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |