6 Tips for Teaching Geometry
1.ज्यामिति के अध्यापन की 6 टिप्स (6 Tips for Teaching Geometry),ज्यामिति का अध्यापन (Teaching of Geometry):
- ज्यामिति के अध्यापन की 6 टिप्स (6 Tips for Teaching Geometry) के आधार पर ज्यामिति को रोचक, सरल व मनोरंजक बना सकते हैं।ज्यामिति गणित की एक महत्वपूर्ण शाखा है। ज्यामिति में बिन्दुओं,रेखाओं,रेखाखंडों, तलों तथा ठोस पिण्डों के गुणों और उनके आकार, विस्तार और स्थिति का अध्ययन किया जाता है।त्रिकोणमिति भी ज्यामिति से ही व्युत्पन्न हुई है।इस शताब्दी में ज्यामिति के पाठ्यक्रम को आधुनिक बनाने हेतु अनेक प्रयास किए गए हैं।वर्तमान ज्यामिति की विषयवस्तु को समुच्चय भाषा में प्रकट कर अधिक उपयोगी बनाया गया है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस - वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:Seven Wonders of World in Mathematics
2.ज्यामिति का अर्थ (The Meaning of Geometry) :
- ज्यामिति दो शब्दों ‘ज्या’ तथा ‘मिति’ से मिलकर बना है।’ज्या’ का अर्थ भूमि तथा ‘मिति’ का अर्थ मापन से है अर्थात् यह गणित की वह शाखा है जिसमें भूमि का माप लिया जाता है।प्राचीनकाल में इस गणित का प्रयोग जीवन के प्रत्येक क्षेत्र में होता था।हम यह भी कह सकते हैं कि ज्यामिति गणित की वह शाखा है जिसमें बिंदु,रेखा,रेखा-खंड,तल एवं ठोसों का अध्ययन उनके आकार,विस्तार तथा स्थिति के रूप में किया जाता है।इसे भूमिति भी कहते हैं जो कि ज्यामिति शब्द का पर्यायवाची है।
3.ज्यामिति का इतिहास (History of Geometry):
- यूनान निवासी आदिम मिश्र के सर्वेक्षकों को ‘ज्यामितिकार’ या ‘भूमापक’ का नाम देते थे।इन ज्यामितिज्ञों ने त्रिभुजों,वर्गों,आयतों और यहां तक की वृत्तों के बारे में ढेर सारे तथ्य प्राप्त किए।इन समस्त तथ्यों ने मिलकर फिर ज्ञान की एक नई विधा को जन्म दिया जिसका नामकरण यूनानियों के हाथों ‘ज्यामिति’ या ‘भूमि मापन संबंधी अध्ययन’ के रूप में हुआ।ज्यामिति के क्षेत्र में उन्होंने महत्वपूर्ण प्रगति की।न केवल मिस्रियों द्वारा स्थापित अनेक दोषपूर्ण नियमों में उन्होंने संशोधन किए अपितु विभिन्न ज्यामितीय आकृतियों का उनके बीच के सह-संबंधों को निकालने के लिए उन्होंने अध्ययन किया।
- यूनानी गणितज्ञ थेल्स जो ढाई हजार वर्ष पूर्व हुए थे ने पता लगाया कि वृत्त के व्यास को चाहे किसी भी रूप में खींचा जाए रेखा वृत्त को हमेशा समद्विभाजित करती है यानी उसे दो बराबर आधे हिस्सों में बांटती है।उसने इस पर भी गौर किया कि दो सरल रेखाएं जब एक दूसरे को काटती है तो आमने-सामने के कोण हमेशा बराबर होते हैं।इनसे यूनानियों को भूमापन के अध्ययन के रूप में स्थापित करने में बड़ी मदद मिली।थेल्स के बाद पाइथागोरस सरीखे यूनानी गणितज्ञों ने ज्यामितीय आकृतियों संबंधी काफी तथ्यों को खोजकर उन्हें सिद्ध करके दिखाया।
- प्राचीनकाल में यूनान के प्रसिद्ध दार्शनिक प्लेटो ने अपने निवास स्थान के बाहर लिख रखा था,”जो व्यक्ति ज्यामिति नहीं जानता वह यहाँ प्रवेश नहीं पा सकता”।ज्यामिति के अध्ययन के लिए अच्छे स्तर की तर्क एवं सोचने की शक्ति की आवश्यकता होती है।प्लेटो ने इसी विचार को ध्यान में रखकर यह नियम बनाया होगा।ज्यामिति के सिद्धांत बहुत प्राचीनकाल से भारत में यज्ञ की वेदी बनाने में तथा ज्योतिष सम्बन्धी गणनाओं में लाये जाते थे।किंतु यूनानी गणितज्ञ यूक्लिड (जो 300 ईसा पूर्व के आसपास सिकंदरिया (अलेक्जेंड्रिया,मिश्र) के संग्रहालय में गणित पढ़ाते थे) पहले गणितज्ञ थे।अपने ग्रंथ ज्यामिति के मूलतत्व (एलिमेंट्स) में एक तार्किक आधार पर ज्यामिति को व्यवस्थित रुप दिया।यूक्लिड की प्रसिद्ध पुस्तक ‘The Elements’ ज्यामितिशास्त्र का स्रोत माना जाता है।यूक्लिड ने मानव इतिहास में प्रथम बार ज्यामिति को औपचारिक स्वरूप प्रदान किया।लगभग 2000 वर्ष तक पृथ्वी के सभी देशों में ज्यामिति का अध्ययन यूक्लीडियन विचार के आधार पर होता रहा है।
- भारत में प्राचीन हिंदू सभ्यता में ज्यामिति का बहुत प्रयोग हुआ।यज्ञ के लिए जो हवन-कुण्ड बनाते थे वे नियमित ज्यामितीय आकृति वाले होते थे।हड़प्पा और मोहनजोदड़ो की संस्कृति की जानकारी से यह सिद्ध हुआ है कि प्राचीन हिंदुओं ने नगर विकास की कला में ज्यामिति का प्रचुर उपयोग किया।सम्राट अशोक ने तीन सिंहोवाला राज्यचिन्ह अपनाया जो इस बात का द्योतक है कि प्राचीन हिंदू सममित आकृतियों से परिचित थे।वृत्त,परिधि एवं व्यास के संबंध का उल्लेख प्राचीन हिन्दू गणितज्ञों की रचनाओं में मिलता है।भारतवर्ष के गणितज्ञों में ब्रह्मगुप्त,भास्कराचार्य,वराहमिहिर,आर्यभट आदि का इस क्षेत्र में अतुलनीय योगदान रहा है।
- यूक्लिड द्वारा ज्यामिति का संगठित विवेचन लगभग 1800 A.D. तक व्यापक रूप से स्वीकार किया जाता रहा।यह सब बीजगणित के अत्यंत धीमे विकास के कारण हुआ लगभग 1600 A.D. के आसपास बीजगणित का स्वरूप संक्षिप्त भाषा के रूप में प्रारंभ हुआ जिसके द्वारा कठिन एवं पेचीदा संबंधों को बीजगणित की भाषा में लिखना संभव हुआ।इसी काल में विश्लेषिक ज्यामिति (Analytical Geometry) की खोज हुई जिससे परंपरागत ज्यामिति की समस्याओं को यांत्रिक तरीके से बीजगणित समस्याओं में प्रकट किया जा सका।
4.यूक्लिड ज्यामिति में प्रमुख अवधारणाएं (Definitions of Basic Terms Given by Euclid):
- यूनान के लोगों ने सर्वप्रथम निगमनात्मक चिंतन से, सुस्पष्ट तथ्यों के आधार पर प्रमेयों को सिद्ध किया। फिर भी 19वीं शताब्दी के आरंभ तक लोगों ने इस प्रणाली को तर्कसंगत आधार प्रदान करने में सफलता प्राप्त नहीं की।
अब आधुनिक गणित में तर्क के आधार पर संरचनाओं का निर्माण किया जाता है जिससे यह स्पष्ट है कि अभीगृहीतों से विभिन्न नियमों को निष्पादित किया जा सकता है तथा इससे समझने की शक्ति का विकास होता है। - यूक्लिड के कुछ आधारभूत पदों की निम्नांकित परिभाषा दी (Definitions of Basic Terms):
(1.)बिंदु (Point):बिंदु की न लंबाई,न चौड़ाई और न मोटाई होती है।इसका आकार नहीं होता है, केवल स्थिति (position) होती है।
(2.)रेखा (Line):रेखा बिना चौड़ाई वाली लंबाई है।
(3.)सीधी रेखा (Straight लाइन):सीधी रेखा वह रेखा है जिसकी दिशा अपनी लंबाई से सदैव एक-सी रहती है।
(4.)वक्र रेखा (Curved Line):वक्र रेखा वह रेखा है जिसकी दिशा अपनी लम्बाई से सर्वत्र एक न रहकर बदलती रहती है।
(5.)तल (Surface):तल में लंबाई और चौड़ाई तो होती है परन्तु मोटाई नहीं होती है।
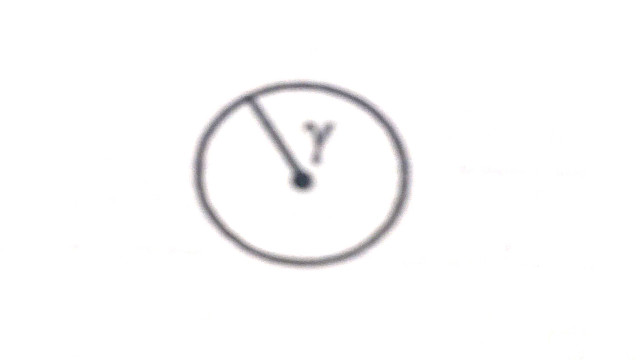
(6.)कोण (Angle):जब दो सरल रेखाएँ अलग दिशाओं से आकर एक बिंदु पर मिलती हैं तो वे उस बिंदु पर एक कोण बनाती है।
(7.)वृत्त (Circle):यदि कोई बिन्दु की किसी स्थिर बिन्दु से उसकी दूरी सदा एक-सी रहे तो उस बिंदु के पथ से घिरी हुई आकृति को वृत्त कहते हैं। - अभिगृहीत (Postulates):यदि कोई ज्यामितीय रचना इतनी सरल हो कि उसके प्रमाण की आवश्यकता न हो और उसे सम्भव मान सकें तो उसे अभिगृहीत कहते हैं।निम्नलिखित अभिगृहीत हैं:
(1.)दो सरल रेखाएँ केवल एक ही बिंदु पर एक दूसरे को काटती है।
- (2.)दो दिए हुए बिंदुओं से होकर केवल एक ही सरल रेखा खींची जा सकती है।
- (3.)किसी सरल रेखा को उसकी सीध में दोनों ओर इच्छानुसार बढ़ाया जा सकता है।
- (4.)दो बिंदुओं को मिलाने वाली रेखा उसके बीच की न्यूनतम दूरी होती है।
(5.)दो सरल रेखाओं में से जो बड़ी रेखा है उसमें से छोटी रेखा के बराबर भाग काटा जा सकता है।
(6.)दी हुई लंबाई की कोई भी सरल रेखा विभाजित की जा सकती है।
(7.)दिए हुए परिणाम का कोई भी कोण सरल रेखा से द्विभाजित किया जा सकता है।
- (8.)किसी दिए हुए बिंदु से किसी दी हुई सरल रेखा पर लम्ब खींचा जा सकता है।
- (9.)किसी दिए हुए बिन्दु से किसी दी हुई सरल रेखा के समांतर रेखा खींची जा सकती है।
- (10.)किसी बिन्दु को केन्द्र मानकर किसी भी त्रिज्या से एक वृत्त खींचा जा सकता है।
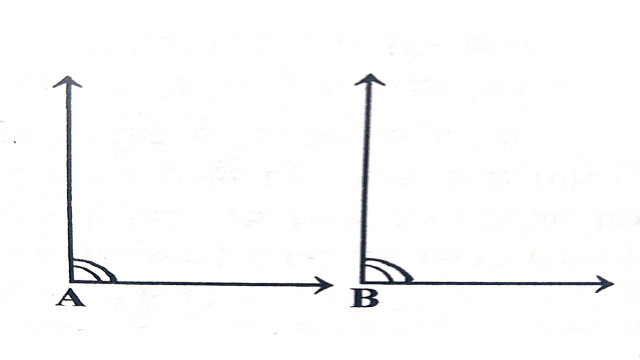
- (11.)सभी समकोण परस्पर समान होते हैं।
- (12.)दो भिन्न रेखाओं में एक से अधिक बिन्दु उभयनिष्ठ नहीं हो सकता है।
- उपर्युक्त अभीगृहीतों परिकल्पित रचनाएँ (Hypothetical Construction) भी कहा जाता है।
- स्वयंसिद्ध (Axioms):ज्यामिति में जिस तर्क की आवश्यकता पड़ती है वह थोड़े से सिद्धांतों एवं परिभाषाओं पर आधारित है।ये सिद्धांत, इतने स्पष्ट, सरल एवं प्रत्यक्ष हैं कि इनकी सत्यता सिद्ध करने की आवश्यकता ही नहीं होती।इन सिद्धान्तों को स्वयंसिद्ध कहते हैं।ज्यामिति के स्वयंसिद्ध:
(1.)जो आकृतियां एक-दूसरे को पूरा-पूरा ढक लेती हैं वे आपस में हर प्रकार से समान होती हैं।
(2.)ज्यामिति की किसी आकृति को बिना रूप तथा आकार बदले एक स्थान से उठाकर दूसरे स्थान पर रख सकते हैं।
(3.)दो सरल रेखाएँ स्थान नहीं घेर सकती।यदि एक सीधी रेखा के दो बिंदु दूसरी सीधी रेखा पर हों तब वे रेखाएँ सब जगह एक-दूसरे के ऊपर पड़ेगी। - यूक्लिड द्वारा रचित ‘The Elements’ के तेरह भाग निम्नलिखित विषय सामग्री प्रस्तुत करते हैं:
प्रथम चार भाग रेखा,कोण, सर्वांगसमता, क्षेत्रफल की धारणाएं स्पष्ट करते हैं और उन्हें त्रिभुज, समान्तर चतुर्भुज,वृत्त, नियमित बहुभुज आकृतियों में प्रयुक्त करते हैं। - भाग पाँच तथा छ:में अनुपात और समानुपात नियम विकसित किए गए हैं।
भाग सात, आठ और नौ में संख्या सिद्धान्त के कुछ नियमों का विवेचन किया गया है तथा पाइथागोरस प्रमेय पर टिप्पणी है।भाग दस में ऐसी परिमेय संख्याओं (Rational Numbers) का उल्लेख हैं जिन्हें वर्गमूलों के रूप में व्यक्त किया जा सकता है।भाग ग्यारह में ठोस ज्यामिति का विवेचन है।भाग बारह में निर्वात विधि का उल्लेख है।भाग तेरह में नियमित ठोस पिण्डों की रचना का वर्णन है। - यूक्लिडियन ज्यामिति में प्रमुख अवधारणाएं:
(1.)अस्तित्व और अद्वितीयता गुणधर्म:यूक्लिड ने बिन्दु,रेखा और तल के अस्तित्व की कल्पना की थी।
(2.)समान्तर गुणधर्म:किसी तल में दी गई दो रेखाएं या तो एक दूसरे को प्रतिच्छेद करती हैं या समांतर होती है।
(3.)सर्वांगसमता (Congruence):यदि दो ज्यामितीय आकृतियां आकार एवं परिणाम में एक जैसी हों तो वे सर्वांगसम होती है।यूक्लिड ने त्रिभुजों की सर्वांगसमता का विवेचन किया है।
(4.)समरूपता (Similarity):दो त्रिभुज समरूप होंगे यदि उनके संगत कोण सर्वांगसम हों और उनकी संगत भुजाएँ समानुपाती हों।
(5.)क्षेत्रफल (Area):यूक्लिड ने अपनी पुस्तक में बंद समतलीय आकृतियों से घिरे क्षेत्रफल के बारे में नियम बताए हैं।
Also Read This Article:Math revolution in the modern age
5.यूक्लिड की ज्यामिति (Euclid’s Geometry):
- यूक्लिड ने सभी प्रकार की ज्यामितीय संकल्पनाओं की परिभाषा से आरंभ किया है जैसे बिंदु,रेखा,तल, कोण,वृत्त आदि।प्रथम परिभाषा इस प्रकार है:
- बिन्दु वह है जिसके कोई संभाग नहीं है।हम इसे किसी भी प्रकार से उपयुक्त परिभाषा नहीं मान सकते हैं क्योंकि बिंदु को केवल इस परिभाषा से ज्ञात नहीं किया जा सकता है।इसी प्रकार हम पढ़ते हैं:रेखा एक लंबाई है जिसकी चौड़ाई नहीं है।यहां पर यह कथन संदिग्ध है,यदि हम वक्र की परिभाषा को ध्यान में रखें जिसके बारे में यूक्लिड को कोई ज्ञान नहीं था।फिर एक सरल रेखा की परिभाषा में बताया गया है कि यह एक रेखा है जो अपनी लंबाई में सदैव एक-सी रहती है।यूक्लिड द्वारा दी गई परिभाषाओं में एक भी परिभाषा सुस्पष्ट नहीं है। उदाहरणार्थ सरल तथा अन्य परिभाषाएं।
- अत:आधुनिक गणित में यूक्लिड की ज्यामिति में सुधार किया गया है।परिणामस्वरूप बिन्दु (Point), आकाश (Space),तल (Surface), रेखा (Line) को अपरिभाषित माना गया है।अब इन शब्दों की परिभाषा देने की आवश्यकता नहीं है।इसके फलस्वरूप अंतर्विरोध समाप्त हो गया है।कोण A=कोण B है,क्या वास्तव में \angle{A} =\angle{B}? [सही कथन {m\angle}{A}={m\angle}{B}
- (2.)इसी प्रकार यूक्लिड ने रेखा एवं रेखा की लंबाई में अंतर स्पष्ट नहीं किया।नई मेट्रिक ज्यामिति में रेखा एवं रेखाखंड की धारणाओं ने इस स्थिति को अत्यंत स्पष्ट कर दिया है।
(3.)यूक्लिड ने प्रयोग एवं अभीगृहीत में स्पष्ट अंतर नहीं किया।
(4.)यूक्लिड ने रेखागणितीय आकृतियों पर अधिक निर्भर किया।’किसी तल पर दो बिंदुओं को मिलाने पर रेखा उस तल का भाग होती है’ जैसी धारणा यूक्लिड विकसित नहीं कर सके।
(5.)परिमेय संख्याओं का यूक्लिड के समय में उपयोग नहीं होता था।इस कारण यूक्लिड की ज्यामिति अपूर्ण रही।
6.ज्यामिति के अध्यापन की टिप्स (Tips for Teaching Geometry):
- ज्यामिति एवं बीजगणित को कठिन विषय समझा जाता है।इनके अध्यापन में अध्यापक की विशेष भूमिका होती है।अन्य विषयों को तो छात्र-छात्राएं स्वयं भी पढ़ सकते हैं परन्तु ज्यामिति एवं बीजगणित में अध्यापक की आवश्यकता होती है। सामान्यतया छात्र-छात्राएं ज्यामिति कि प्रमयों को रट लेते हैं जिससे छात्र-छात्राओं की बुद्धि का उचित निकास नहीं होता है।गणित अध्यापक अपनी सूझ-बूझ,चतुराई एवं दक्षता से ज्यामिति को रोचक बना सकता है।प्रारंभिक कक्षाओं से ही बालकों को गणित की विषयवस्तु दैनिक जीवन से संबंधित करके पढ़ाया जाए।जैसे: घन व घनाभ के लिए माॅडल्स का प्रयोग किया जा सकता है।अथवा कमरे,आलमारी व माचिस की डिब्बी को दिखाकर इसके प्रत्ययों को स्पष्ट किया जा सकता है।उच्च कक्षाओं में छात्र-छात्राओं में तर्क व चिन्तन शक्ति का विकास हो चुका होता है अत:अमूर्त परिभाषा, कथनों द्वारा उनको समझाया जा सकता है।प्रमेयों, सवालों तथा समस्याओं का छात्र-छात्राओं को अभ्यास कराया जाए जिससे उनके प्रत्यय स्पष्ट हो सकें।गृहकार्य भी दिया जाए जिससे उनके प्रत्यय स्पष्ट हो सकें।यदि पिछली कक्षा की कमियां रह गई है तो सम्बन्धित टाॅपिक अथवा पुस्तक आरम्भ करने से पहले पिछली कक्षाओं के मुख्य-मुख्य बिन्दुओं, परिभाषाओं को स्पष्ट किया जाए, समझाया जाए।इसके पश्चात पाठ्यक्रम का सम्बन्धित टाॅपिक पढ़ाया जाए।छात्र-छात्राओं को प्रेरित करते रहना चाहिए तथा उनकी बुद्धि, तर्क शक्ति व चिन्तन-मनन करने की शक्ति के विकास पर ध्यान देना चाहिए।
- उपर्युक्त आर्टिकल में ज्यामिति के अध्यापन की 6 टिप्स (6 Tips for Teaching Geometry),ज्यामिति का अध्यापन (Teaching of Geometry) के बारे में बताया गया है।
7.विद्यार्थी द्वारा गणित की कक्षा में ध्यान न देना (हास्य-व्यंग्य) (Student Not Paying Attention in Mathematics) (Humour – Satire) :
6 Tips for Teaching Geometry
- पिता:अविनाश स्कूल से रोते हुए क्यों आ रहे हो?
- अविनाश:मैं गणित के पीरियड में चुपचाप बैठा हुआ था,किसी से बातचीत भी नहीं कर रहा था।अचानक गुरुजी मेरे पास आए और बोले तुम्हारा ध्यान कहां है,किन ख्यालों में खोए हुए हो?गणित के सवालों को समझने में ध्यान क्यों नहीं लगा रहे हो? जब मैंने कोई जवाब नहीं दिया तो उन्होंने मेरी पिटाई कर दी साथ ही हिदायत दी कि यदि अब भी तुमने ध्यान नहीं दिया तो तुम्हारी शिकायत प्रधानाचार्यजी से कर दी जाएगी।प्रधानाचार्यजी इससे भी ज्यादा पेनल्टी दे सकते हैं,हो सकता है तुम्हे स्कूल से ही निकाल दिया जाए।
- पिता:तुम स्कूल में पढ़ने जाते हो तो पढ़ने में ध्यान लगाया करो।आखिर तुम्हें प्राइवेट स्कूल में दाखिला कराया है और स्कूल की मोटी फीस भी चुकानी पड़ती है।तुम्हें उसका भी कुछ ख्याल नहीं है।अपने मन को इधर-उधर भटकाओगे तथा ध्यान नहीं दोगे तो गुरुजी ने तुम्हें सावधान व सचेत करने के लिए एक दो-थप्पड़ लगा दिए तो इसमें क्या गलत कर दिया है?
- अविनाश:परंतु मैं क्लास में शोर-शराबा,बातचीत या कोई गड़बड़ तो नहीं कर रहा था।कक्षा की शांति तो भंग नहीं कर रहा था।कक्षा के वातावरण को तो नहीं बिगाड़ रहा था।
- पिता:यह तो तुम ठीक कर रहे थे परंतु पढ़ाई करने के लिए केवल इतना ही पर्याप्त नहीं है कि शांति से चुपचाप कक्षा में बैठे रहो।बल्कि यह भी आवश्यक है कि पढ़ाई में अपना दिल और दिमाग दोनों को लगाओ।गणित विषय वैसे भी कठिन विषय है।इसे तुम अपने स्तर पर स्वयं तो हल नहीं कर पाओगे।परीक्षा में कम अंक आएंगे तो गुरुजी को या माता-पिता को दोष दोगे।मन को पूर्ण एकाग्र करके अभी से ध्यान लगाओ।गुरुजी ने जो हिदायत दी है उसका पालन करोगे तो तुम्हारे हित में ही है वरना बाद में पछताओगे।तुम्हें जीवन में आने वाली कठिनाइयों, परेशानियों का मुकाबला करने का तजुर्बा नहीं है।अभी तुम माता-पिता पर आश्रित हो।तुम पढ़ रहे हो इसलिए माता-पिता,अभिभावक,शिक्षक तथा तुम्हारे शुभचिंतक सहयोग करेंगे लेकिन बाद में यह सभी सहारे छूट जाएंगे तब संसार की वास्तविकता से पाला पड़ेगा तो तुम्हें पढ़ाई के दिन याद आएंगे। अपनी की गई लापरवाही और गलतियों पर पछताओगे लेकिन तब कुछ भी नहीं हो सकता है।
8.ज्यामिति के अध्यापन की 6 टिप्स (6 Tips for Teaching Geometry),ज्यामिति का अध्यापन (Teaching of Geometry) के संबंध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.स्वयं सिद्धियां किसे कहते हैं? (What are the Axioms Called?):
उत्तर:ज्यामिति में जिस तर्क की आवश्यकता पड़ती है वह थोड़े से सिद्धांतों एवं परिभाषाओं पर आधारित है।ये सिद्धांत, इतने स्पष्ट, सरल एवं प्रत्यक्ष हैं कि इनकी सत्यता सिद्ध करने की आवश्यकता ही नहीं होती।इन सिद्धान्तों को स्वयंसिद्ध कहते हैं।
प्रश्न:2.अभिगृहीत किसे कहते हैं? (What is Called Postulate?):
उत्तर:यदि कोई ज्यामितीय रचना इतनी सरल हो कि उसके प्रमाण की आवश्यकता न हो और उसे सम्भव मान सकें तो उसे अभिगृहीत कहते हैं।
प्रश्न:3.ठोस ज्यामिति से क्या तात्पर्य है? (What is Meant by Solid Geometry?):
उत्तर:ठोसों एवं उनके भाग खण्डों से संबंधित गुणों और मापों का अध्ययन करने वाली ज्यामिति की शाखा को ठोस ज्यामिति कहते हैं।
जब समतल पर खींची गई आकृतियों में मोटाई भी सम्मिलित की जाती हैं तो वे ठोस आकार की हो जाती है क्योंकि ठोस में तीन आयाम होते हैं।ठोस में तीन आयामों के कारण निम्नांकित अवयव होते हैं:
(1.)लम्बाई,चौड़ाई,मोटाई
(2.)क्षेत्रफल
(3.)आयतन
इसकी विषय-सामग्री में समान्तर षट्फलक,प्रिज्म, बेलन, पिरामिड, गोला आदि का अध्ययन किया जाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा ज्यामिति के अध्यापन की 6 टिप्स (6 Tips for Teaching Geometry),ज्यामिति का अध्यापन (Teaching of Geometry) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
6 Tips for Teaching Geometry
ज्यामिति के अध्यापन की 6 टिप्स
(6 Tips for Teaching Geometry)
6 Tips for Teaching Geometry
ज्यामिति के अध्यापन की 6 टिप्स (6 Tips for Teaching Geometry) के
आधार पर ज्यामिति को रोचक, सरल व मनोरंजक बना सकते हैं।
ज्यामिति गणित की एक महत्वपूर्ण शाखा है। ज्यामिति में बिन्दुओं
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
