1.त्वरण के स्पर्शरेखीय तथा अभिलाम्बिक घटक (Tangential and normal components of acceleration,Tangential and normal components of velocity and acceleration)-

त्वरण के स्पर्शरेखीय तथा अभिलाम्बिक घटक (Tangential and normal components of acceleration),स्पर्शरेखीय तथा अभिलाम्बिक वेग पर निर्भर करता है।
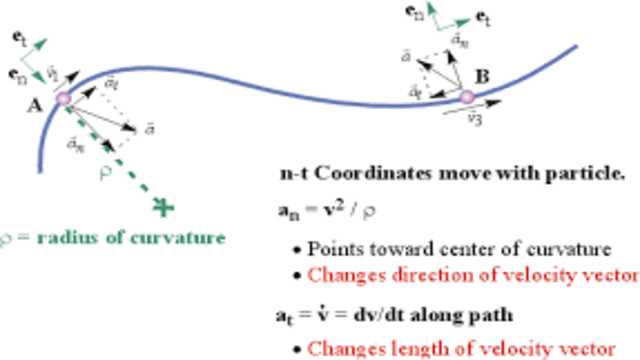
स्पर्शरेखीय त्वरण वेग वेक्टर के परिमाण में परिवर्तन की दर का माप है, अर्थात गति और अभिलाम्बिक त्वरण वेग वेक्टर की दिशा के परिवर्तन की दर का एक माप है।

आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Rectilinear Motion in Resisting Medium

2.आप स्पर्शरेखीय और अभिलाम्बिक त्वरण कैसे ज्ञात करते हैं? (How do you find tangential and normal acceleration?)-
(1.)स्पर्शरेखीय तथा अभिलाम्बिक वेग (Tangential and Normal velocities)-

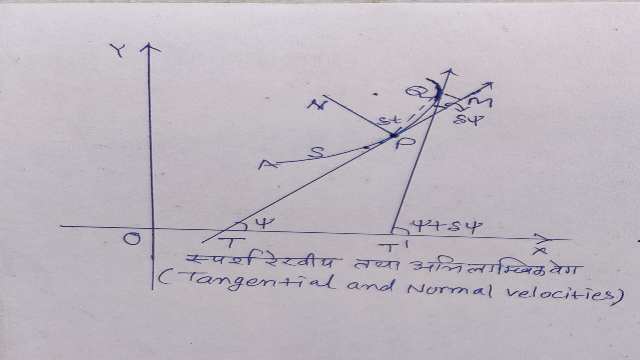
मान लो वक्र पर एक स्थिर बिन्दु A है तथा इस पर चलता हुआ कोई कण t समय पर P बिन्दु पर पहुंचता है, जहां चाप AP=s।मानलो कि कण t+\delta t समय पर बिन्दु Q पर है, जहां चाप PQ= \delta s
यह भी मानलो कि वक्र के बिन्दु P पर स्पर्श रेखा x-अक्ष के साथ \psi कोण बनाती है।यदि Q से,P बिन्दु पर खींची गई स्पर्शरेखा पर QM लम्ब डालें तब कण का समय में P पर स्पर्शरेखा के अनुदिश विस्थापन PM होगा।

अतः P पर स्पर्शरेखीय वेग (Tangential Velocity)
=\begin{matrix} lim \\ \delta t\rightarrow 0 \end{matrix}\frac { \delta t समय \quad में  P पर \quad स्पर्शरेखा \quad के \quad अनुदिश \quad विस्थापन}{ \delta t } \\ =\begin{matrix} lim \\ \delta t\rightarrow 0 \end{matrix}\frac { PM }{ \delta t } \\ =\begin{matrix} lim \\ \delta t\rightarrow 0 \end{matrix}\frac { जीवाPQ\quad \cos { QPM } }{ \delta t } \\ =\begin{matrix} lim \\ \delta t\rightarrow 0 \end{matrix}\frac { जीवाPQ\quad }{ \delta s } .\frac { \delta s }{ \delta t } \cos { QPM } \\ =1.\frac { \delta s }{ \delta t } .1
[ \because जब \quad Q \rightarrow P  तब  \frac {जीवा  PQ}{ \delta s } =1 तथा \angle QPM\rightarrow 0 ]
P पर स्पर्शरेखीय वेग=\frac { ds }{ dt } =\overset { \bullet }{ s }
अब यदि PN ,P पर अन्दर की ओर अभिलम्ब (अवतल दिशा की ओर) हो,तब \delta t समय में PN के समान्तर विस्थापन MQ होगा।
अतः P पर अभिलाम्बिक वेग (Normal Velocity)
= \lim _{ \delta t\rightarrow 0 }{ \frac { MO\quad }{ \delta t } } \\ =\lim _{ \delta t\rightarrow 0 }{ \frac { जीवाPQ\sin { QPM } \quad }{ \delta t } } \\ =\lim _{ \delta t\rightarrow 0 }{ \frac { जीवाPQ\quad }{ \delta s } } .\frac { \delta s\quad }{ \delta t } \sin { QPM } \\ =1.\frac { \delta s\quad }{ \delta t } .0
[\because जब\quad Q\rightarrow P ,तब \frac { जीवा PQ\quad }{ \delta s } =1  तथा \angle QPM\rightarrow 0 ]
P पर अभिलाम्बिक वेग=0
अतः एक कण जो समतल में किसी वक्र के अनुदिश गमन करता है,का स्पर्शरेखीय वेग \frac { ds }{ dt } तथा अभिलाम्बिक वेग 0 होता है।

(2.)त्वरण के स्पर्शरेखीय तथा अभिलाम्बिक घटक (Tangential and normal components of acceleration,Tangential and normal components of velocity and acceleration),त्वरण के स्पर्शरेखीय घटक का सूत्र (Tangential component of acceleration formula)-

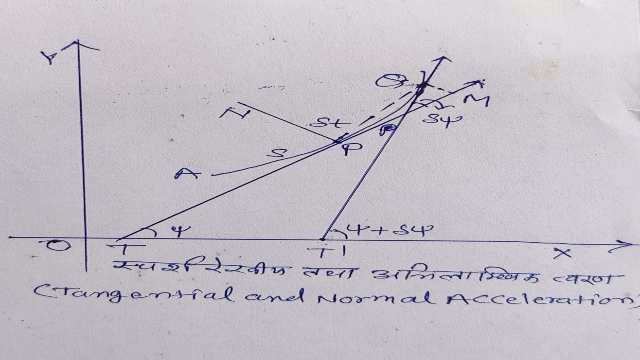
मान लो t व t+\delta t समय पर कण की स्थिति बिन्दु P व Q पर है।मानलो P व Q पर कण का वेग क्रमशः V तथा t+\delta Vहै।यह भी मानलो कि P व Q पर खींची PT व QT' x-अक्ष के साथ क्रमशः कोण \psi  व \psi +\delta \psi बनाती है तब स्पर्श रेखाओं के मध्य का कोण होगा।

अतः समय अन्तराल में TP के अनुदिश वेग में परिवर्तन
=(Q पर TP के अनुदिश वेग)-(P पर TP के अनुदिश वेग)

= \left( v+\delta v \right) \cos { \delta \psi } -v\\ =\left( v+\delta v \right) .1-v\\ =\delta v[ \delta \psi छोटा है,\therefore \cos { \delta \psi } \rightarrow 1]
इसी प्रकार समय अन्तराल में TP के लम्बवत वेग में परिवर्तन
=Q पर TP के लम्बवत वेग-P पर TP के लम्बवत वेग

= \left( v+\delta v \right) \sin { \delta \psi } -0\\ =\left( v+\delta v \right) \delta \psi \\ =v\delta \psi [ \delta \psi छोटा है,\therefore \sin { \delta \psi } \rightarrow \delta \psi ,\delta v\delta \psi \rightarrow 0]
अतः P पर स्पर्शरेखीय त्वरण (Tangential Acceleration)
=\lim _{ \delta t\rightarrow 0 }{ \frac { \delta t समय \quad अन्तराल \quad में P के \quad अनुदिश \quad वेग \quad में \quad परिवर्तन}{ \delta t } } \\ =\lim _{ \delta t\rightarrow 0 }{ \frac { \delta v }{ \delta t } } \\ =\frac { dv }{ dt } =\frac { d }{ dt } \left( \frac { ds }{ dt } \right) \\ =\frac { { d }^{ 2 }s }{ d{ t }^{ 2 } } =\frac { dv }{ ds } .\frac { ds }{ dt } =v\frac { dv }{ ds }
अतः स्पर्शरेखीय त्वरण= \frac { dv }{ dt } =\frac { { d }^{ 2 }s }{ d{ t }^{ 2 } } =v\frac { dv }{ ds }
तथा P पर अभिलाम्बिक त्वरण (Normal Acceleration)
= \lim _{ \delta t\rightarrow 0 }{ \frac { \delta t समय \quad अन्तराल \quad में TP के \quad लम्बवत \quad वेग \quad में \quad परिवर्तन}{ \delta t } } \\ \lim _{ \delta t\rightarrow 0 }{ v\frac { \delta \psi }{ \delta t } } \\ =v\frac { d\psi }{ dt } \\ =v\frac { d\psi }{ ds } .\frac { ds }{ dt } =v.\frac { 1 }{ \rho } .v=\frac { { v }^{ 2 } }{ \rho }
[\because \rho =\frac { ds }{ d\psi } जहां \rho वक्र के बिन्दु P पर वक्रता त्रिज्या]
अतः अभिलाम्बिक त्वरण=\frac { { v }^{ 2 } }{ \rho }
टिप्पणी:स्पर्शरेखीय वेग तथा त्वरण की धनात्मक दिशा के बढ़ने की दिशा में होगी तथा अभिलाम्बिक त्वरण अभिलम्ब के अनुदिश अन्दर की तरफ होगा।
विशेष स्थिति (Particular Case): यदि कण एक वृत्तीय पथ (Circular Path) पर चले तो s=a\theta तथा \rho =a
स्पर्शरेखीय वेग \frac { ds }{ dt } =a\dot { \theta } अनुप्रस्थ वेग

अभिलाम्बिक त्वरण=0=अरीय वेग
स्पर्शरेखीय त्वरण= \frac { { d }^{ 2 }s }{ d{ t }^{ 2 } } =a\ddot { \theta } अनुप्रस्थ त्वरण
अभिलाम्बिक त्वरण=\frac { { v }^{ 2 } }{ \rho } =\frac { { \left( a\dot { \theta } \right) }^{ 2 } }{ \rho } =a{ \dot { \theta } }^{ 2 } अरीय त्वरण

3.त्वरण के स्पर्श रेखीय तथा अभिलाम्बिक घटकों की हल सहित समस्याएं (Tangential and normal components of acceleration Solved Problems)-

Example-1.सिद्ध करो कि एक समतल वक्र में एकसमान चाल से चलने वाले बिन्दु का त्वरण \rho { \dot { \psi } }^{ 2 } होगा।
(Prove that the acceleration of a point moving in a plane curve with uniform speed is \rho { \dot { \psi } }^{ 2 } )
Solution-समान चाल=\sqrt { { \left( \frac { ds }{ dt } \right) }^{ 2 }+{ 0 }^{ 2 } } =c\\ \Rightarrow \frac { ds }{ dt } =c\\ \Rightarrow \frac { dv }{ dt } =\frac { { d }^{ 2 }s }{ d{ t }^{ 2 } } =0
अभिलाम्बिक त्वरण (Normal Acceleration)=\frac { { v }^{ 2 } }{ \rho }
स्पर्शरेखीय त्वरण (Tangential Acceleration)=\frac { dv }{ dt } =0
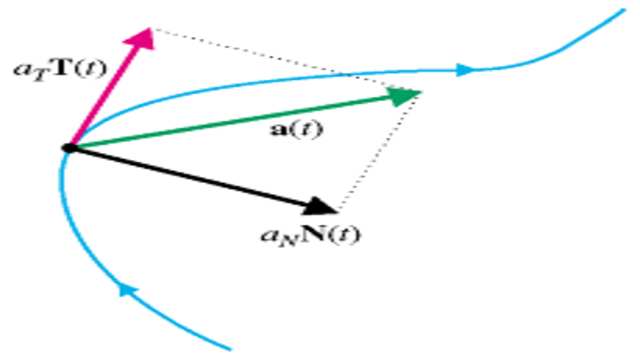
अतः परिणामी त्वरण (Resultant Acceleration)=\sqrt { { \left( \frac { { v }^{ 2 } }{ \rho } \right) }^{ 2 }+{ \left( \frac { dv }{ dt } \right) }^{ 2 } } \\ =\frac { { v }^{ 2 } }{ \rho } ......(1)\\ \frac { d\psi }{ dt } =\frac { d\psi }{ ds } .\frac { ds }{ dt } =\frac { v }{ \rho } \\ \Rightarrow v=\rho \dot { \psi } .......(2)
समीकरण (1) व (2) से-

त्वरण (Acceleration)=\frac { { \left( \rho \dot { \psi } \right) }^{ 2 } }{ \rho } \\ ={ \rho \dot { \psi } }^{ 2 }

Example-2.एक बिन्दु अचर वेग से किसी वक्र में चलता है और P तथा एक स्थिर बिन्दु O को मिलानेवाली ध्रुवान्तर रेखा का कोणीय वेग,OP के व्युत्क्रमानुपाती होता है। प्रदर्शित करिए कि वक्र O ध्रुव वाला एकसमान कोणिक सर्पिल है और P का अभिलाम्बिक त्वरण,OP के व्युत्क्रमानुपाती है।
(A point P describes a curve with a constant velocity and the radius vector joining P to a fixed point O has an angular velocity which is inversely proportional to OP.Show that the curve is an equiangular spiral with O as pole and acceleration of P along normal varies inversely as OP.)
Solution-दिया हुआ है v=k (अचर)

\frac { d\theta }{ dt } =\frac { c }{ r } ,OP=r\\ v=\sqrt { \left\{ { \left( \frac { dr }{ dt } \right) }^{ 2 }+{ r }^{ 2 }{ \left( \frac { d\theta }{ dt } \right) }^{ 2 } \right\} } \\ =\sqrt { { \left( \frac { dr }{ dt } \right) }^{ 2 }+{ r }^{ 2 }.\frac { { c }^{ 2 } }{ { r }^{ 2 } } } \\ \Rightarrow v=\sqrt { { \left( \frac { dr }{ dt } \right) }^{ 2 }+{ c }^{ 2 } } =k
दोनों पक्षों का वर्ग करने पर-

{ \left( \frac { dr }{ dt } \right) }^{ 2 }+{ c }^{ 2 }={ k }^{ 2 }\\ \Rightarrow { \left( \frac { dr }{ dt } \right) }^{ 2 }={ k }^{ 2 }-{ c }^{ 2 }={ B }^{ 2 }(माना)\\ \Rightarrow \frac { dr }{ dt } =B\quad तथा\quad \frac { d\theta }{ dt } =\frac { c }{ r } \\ \Rightarrow \frac { \frac { dr }{ dt } }{ \frac { d\theta }{ dt } } =\frac { Br }{ c } \\ \Rightarrow \frac { dr }{ d\theta } =\frac { Br }{ c } \\ \Rightarrow \frac { dr }{ r } =\frac { B }{ c } d\theta
समाकलन करने पर-

\Rightarrow \log { r } =\frac { B\theta }{ c } +\log { D } \\ \Rightarrow \log { \left( \frac { r }{ D } \right) } =\frac { B\theta }{ c } \\ \Rightarrow r={ e }^{ \left( \frac { BD }{ c } \right) \theta }\\ r={ e }^{ m\theta }\left[ माना\quad m=\frac { BD }{ c } \right]
जो कि समानकोणिक सर्पिल है।

हम जानते हैं कि कोणिक सर्पिल

r=a{ e }^{ \theta \cot { \alpha } }
तथा ध्रुवीय समीकरण p =r\sin { \alpha } \\ \rho =r\frac { dr }{ dp } \\ \Rightarrow \rho =\frac { r }{ \left( \frac { dp }{ dr } \right) } \\ \Rightarrow \rho =\frac { r }{ \sin { \alpha } } \\ \Rightarrow \rho =rcosec\alpha
अभिलाम्बिक त्वरण=\frac { { v }^{ 2 } }{ \rho } \\ \frac { { v }^{ 2 } }{ \rho } =\frac { { k }^{ 2 } }{ rcosec\alpha } \\ \Rightarrow \frac { { v }^{ 2 } }{ \rho } \alpha \frac { 1 }{ r }
अभिलाम्बिक त्वरण ध्रुवान्तर रेखा OP अर्थात् r के व्युत्क्रमानुपाती है।

Example-3.एक बिन्दु P ध्रुव O के सापेक्ष अचर कोणीय वेग से एकसमान कोणिक सर्पिल r=a{ e }^{ \theta \cot { \alpha } } में गमन करता है।सिद्ध कीजिए कि इसका त्वरण OP के समानुपाती है तथा उसकी दिशा P पर स्पर्शरेखा से वही अचर कोण बनाती है जो OP उस स्पर्शरेखा से बनाती है।
(A point P describes an equiangular spiral r=a{ e }^{ \theta \cot { \alpha } } with constant angular velocity about the pole O. Show that its acceleration varies as OP and is in a direction making with the tangent at P the same constant angle that OP makes with the tangent.)
Solution-दिया हुआ है \frac { d\theta }{ dt } =c (माना)…(1)

\frac { { d }^{ 2 }\theta }{ d{ t }^{ 2 } } =0\\ r=a{ e }^{ \theta \cot { \alpha } }\\ \frac { dr }{ dt } =a\cot { \alpha } { e }^{ \theta \cot { \alpha } }\frac { d\theta }{ dt } \\ \Rightarrow \frac { dr }{ dt } =cr\cot { \alpha } .............(2)
पुनः अवकलन करने पर-

\frac { { d }^{ 2 }r }{ d{ t }^{ 2 } } =ca\cot ^{ 2 }{ \alpha } { e }^{ \theta \cot { \alpha } }\frac { d\theta }{ dt } \\ \frac { { d }^{ 2 }r }{ d{ t }^{ 2 } } =r{ c }^{ 2 }\cot ^{ 2 }{ \alpha }
अरीय त्वरण (Radial Acceleration)[R.A.]=\frac { { d }^{ 2 }r }{ d{ t }^{ 2 } } -r{ \left( \frac { d\theta }{ dt } \right) }^{ 2 }\\ =r{ c }^{ 2 }\cot ^{ 2 }{ \alpha } -r{ c }^{ 2 }\\ R.A.=r{ c }^{ 2 }\left( \cot ^{ 2 }{ \alpha } -1 \right) .....(3)
अनुप्रस्थ त्वरण (Tranverse Acceleration)[T.A.]=2\left( \frac { dr }{ dt } \right) \left( \frac { d\theta }{ dt } \right) +r\left( \frac { { d }^{ 2 }\theta }{ d{ t }^{ 2 } } \right) \\ =2\left( cr\cot { \alpha } \right) \left( c \right) +r\left( 0 \right) \\ T.A.=2{ c }^{ 2 }r\cot { \alpha } .........(4)
परिणामी त्वरण (Resultant Acceleration)==\sqrt { { \left( R.A. \right) }^{ 2 }+{ \left( T.A. \right) }^{ 2 } } \\ =\sqrt { { \left\{ r{ c }^{ 2 }\left( \cot ^{ 2 }{ \alpha } -1 \right) \right\} }^{ 2 }+\left\{ 4{ c }^{ 4 }{ r }^{ 2 }\cot ^{ 2 }{ \alpha } \right\} } \\ =\sqrt { { r }^{ 2 }{ c }^{ 4 }\left[ { \left( \cot ^{ 2 }{ \alpha } -1 \right) }^{ 2 }+4\cot ^{ 2 }{ \alpha } \right] } \\ =r{ c }^{ 2 }\sqrt { \cot ^{ 4 }{ \alpha } -2\cot ^{ 2 }{ \alpha } +1+4\cot ^{ 2 }{ \alpha } } \\ =r{ c }^{ 2 }\sqrt { \cot ^{ 4 }{ \alpha } +2\cot ^{ 2 }{ \alpha } +1 } \\ =r{ c }^{ 2 }\sqrt { { \left( \cot ^{ 2 }{ \alpha } +1 \right) }^{ 2 } } \\ =r{ c }^{ 2 }\left( 1+\cot ^{ 2 }{ \alpha } \right) \\ =r{ c }^{ 2 }{ cosec }^{ 2 }\alpha
अतः परिणामी त्वरण OP अर्थात् ध्रुवान्तर रेखा r के समानुपाती है।यदि परिणामी त्वरण अरीय दिशा के साथ \beta कोण बनाता है तो

\tan { \beta } =\frac { T.A. }{ R.A. } \\ =\frac { 2{ c }^{ 2 }r\cot { \alpha } }{ r{ c }^{ 2 }\left( \cot ^{ 2 }{ \alpha } -1 \right) } \\ =\frac { 2\tan { \alpha } }{ 1-\tan ^{ 2 }{ \alpha } } \\ =\tan { 2\alpha } \\ \Rightarrow \beta =2\alpha
पुनः r=a{ e }^{ \theta \cot { \alpha } }\\ \log { r } =\log { a } +\theta \cot { \alpha }
के सापेक्ष अवकलन करने पर-

\frac { 1 }{ r } \frac { dr }{ d\theta } =0+\cot { \alpha } \\ \cot { \phi } =\cot { \alpha } \\ \phi =\alpha
अतः स्पर्शरेखा ध्रुवान्तर रेखा OP के साथ \alpha कोण बनाती है।
त्वरण की दिशा,स्पर्शरेखा के साथ कोण बनाती है=ध्रुवान्तर रेखा के साथ कोण-ध्रुवान्तर रेखा के साथ स्पर्शरेखा का कोण

=\beta -\phi \\ =2\alpha -\alpha \\ =\alpha
Example-4.एक कण वृत्त के व्यास AB पर अचर वेग से चलता है और एक अन्य कण विरामावस्था से अर्धपरिधि AB पर एकसमान स्पर्शरेखीय त्वरण से चलता है।यदि वे A से एक साथ रवाना होते हैं और B पर साथ-साथ पहुंचते हैं तो सिद्ध करो कि B पर उनके वेग \pi :1 अनुपात में होंगे।
(One point describes the diameter AB of a circle with constant Velocity and another semi-circumference AB from rest with constant tangential acceleration.If they starts together from A and arrive together at B,Show that the velocities at B are in the ratio \pi :1)
Solution-माना A पर कण के पहुंचने में लिया गया समय t है।यदि व्यास OA पर एकसमान चाल u से चलता है तब
OA=2a=ut, \therefore t=\frac { 2a }{ u } ....(1)\\ \frac { { d }^{ 2 }s }{ { dt }^{ 2 } } =\frac { dv }{ dt } =v\frac { dv }{ ds } =k\\ \Rightarrow vdv=kds
समाकलन करने पर-

\frac { { v }^{ 2 } }{ 2 } =ks+B
प्रारम्भ में जब s=0,v=0
प्रारम्भ में विरामावस्था से प्रारम्भ होता है तो B=0

{ v }^{ 2 }=2ks
यदि A पर पहुंचने पर चाल V है तो
S=a\pi =(अर्धवृत्त की परिधि)

{ V }^{ 2 }=2ka\pi …..(2)
पुनः \frac { dv }{ dt } =k लेने पर-
dv=kdt
समाकलन करने पर-
v=kt+C
जब t=0,v=0 तब C=0
v=kt
परन्तु जब t=\frac { 2a }{ u } [(1) से] तब v=V
दोनों कण एकसाथ पहुंचते हैं

V=k.\frac { 2a }{ u } \Rightarrow k=\frac { uV }{ 2a }
समीकरण (2) में मान रखने पर-

{ V }^{ 2 }=2a\pi \frac { uV }{ 2a } \\ \Rightarrow \frac { V }{ u } =\frac { \pi }{ 1 } \\ V:u=\pi :1
Example-5. a लम्बाई की एक सीधी व चिकनी छड़ पर छड़ के एक सिरे O से b दूरी पर एक छल्ला विरामावस्था में है।छड़ को अचानक क्षैतिज समतल में सिरे O के सापेक्ष अचर कोणीय वेग w से घुमाया जाता है।सिद्ध कीजिए कि छल्ला (\frac { 1 }{ \omega } )\cosh ^{ -1 }{ (\frac { a }{ b } ) }  समय पश्चात् वेग से छड़ को छोड़ देगा।
(A small ring is at rest on a smooth straight horizontal rod of length a at distance from one end of the rod.The rod is then suddenly set roatating in a horizontal plane about the end O with constant angular velocity w. Prove that the ring will leave the rod with velocity after a time (\frac { 1 }{ \omega } )\cosh ^{ -1 }{ (\frac { a }{ b } ) } .)
Solution-छल्ला विरामावस्था में है अतः त्वरण शून्य होगा-

\frac { { d }^{ 2 }r }{ { dt }^{ 2 } } -r{ (\frac { d\theta }{ dt } ) }^{ 2 }=0\\ \Rightarrow \frac { { d }^{ 2 }r }{ { dt }^{ 2 } } =r{ (\frac { d\theta }{ dt } ) }^{ 2 }\\ \Rightarrow \frac { { d }^{ 2 }r }{ { dt }^{ 2 } } =r{ \omega }^{ 2 }
दोनों पक्षों को 2\frac { dr }{ dt } से गुणा करने पर-

2(\frac { dr }{ dt } )(\frac { { d }^{ 2 }r }{ { dt }^{ 2 } } )=2r(\frac { dr }{ dt } ){ \omega }^{ 2 }
समाकलन करने पर-

{ (\frac { dr }{ dt } ) }^{ 2 }={ r }^{ 2 }{ \omega }^{ 2 }+c
प्रारम्भ में जब r=b,\frac { dr }{ dt } =0,\therefore c=-{ b }^{ 2 }{ { \omega } }^{ 2 }\\ { (\frac { dr }{ dt } ) }^{ 2 }={ { \omega } }^{ 2 }({ r }^{ 2 }-{ b }^{ 2 })...(1)
छल्ला छड़ को छोड़ देगा जब यह छड़ की लम्बाई a के अन्त पर पहुंचता है।अत समीकरण (1) से

{ (\frac { dr }{ dt } ) }^{ 2 }={ { \omega } }^{ 2 }({ a }^{ 2 }-{ b }^{ 2 })....(2)
छल्ले का अनुप्रस्थ वेग जब छल्ला छड़ को छोड़ देता है अर्थात् r=a

r(\frac { d\theta }{ dt } )=a\omega
परिणामी वेग(Resultant Velocity) v={ (\frac { dr }{ dt } ) }^{ 2 }+{ (r\frac { d\theta }{ dt } ) }^{ 2 }\\ ={ { \omega } }^{ 2 }[{ a }^{ 2 }-{ b }^{ 2 }+{ a }^{ 2 }]\\ v=\omega \sqrt { { 2a }^{ 2 }-{ b }^{ 2 } }
समय (Time):-\frac { dr }{ dt } =\omega \sqrt { { r }^{ 2 }-{ b }^{ 2 } } \\ \int _{ b }^{ a }{ \frac { dr }{ b\sqrt { { r }^{ 2 }-{ b }^{ 2 } } } } =\int { \omega dt } \\ { [\cosh ^{ -1 }{ (\frac { r }{ b } ) } ] }_{ b }^{ a }=\omega t\\ t=(\frac { 1 }{ \omega } )\cosh ^{ -1 }{ (\frac { a }{ b } ) }
उपर्युक्त उदाहरणों के द्वारा त्वरण के स्पर्शरेखीय तथा अभिलाम्बिक घटक (Tangential and normal components of acceleration,Tangential and normal components of velocity and acceleration) को समझ सकते हैं।

4.त्वरण के स्पर्श रेखीय तथा अभिलाम्बिक घटक की समस्याएं (Tangential and normal components of acceleration Problems)-

(1.)एक कण किसी वक्र पर इस प्रकार चलता है कि इसके स्पर्शरेखीय एवं अभिलाम्बिक त्वरण आपस में समानुपातिक है एवं उसकी स्पर्शरेखा का कोणीय वेग अचर रहता है।वक्र ज्ञात कीजिए।
(A particle moves in a curve so that its tangential and normal acceleration are proportional to each other and the angular velocity of the tangent is constant. Find the curve.)
(2.)एक कण समतल वक्र में इस प्रकार चलता है कि इसके स्पर्शरेखीय तथा अभिलाम्बिक त्वरण सदैव समान रहते हैं और इसका वेग { e }^{ \tan ^{ -1 }{ (\frac { s }{ c } ) } } के समानुपाती है जहां s किसी स्थिर बिन्दु से मापी गई चाप की लम्बाई है।सिद्ध करो कि पथ केटेनरी है।
(A paricle moves in a plane curve in such a manner that its tangential and normal accelerations are always equal and its Velocity varies as { e }^{ \tan ^{ -1 }{ (\frac { s }{ c } ) } },s being the length of the curve measured from the fixed point on the curve. Show that the path is catenary.)
(3.)एक कण एक समतल वक्र में इस प्रकार गमन करता है कि इसका स्पर्शरेखीय त्वरण अचर रहता है और इसके स्पर्शरेखीय वेग का परिणाम तथा अभिलाम्बिक त्वरण का अनुपात अचर रहता है।सिद्ध करो कि पथ का नैज समीकरण S=A{ \psi }^{ 2 }+B\psi +C रूप में होगा।
(A point moves in a plane curve so that its tangential acceleration is constant and the magnitude of the tangential velocity and normal acceleration are in a constant ratio. Show that the intrinsic equation of the path is of the form S=A{ \psi }^{ 2 }+B\psi +C.)
(4.)एक कण एकसमान कोणीय वेग से किसी परवलय में उसकी नाभि के चारों ओर चलता है।सिद्ध करो कि किसी बिन्दु पर अभिलाम्बिक त्वरण उस बिन्दु पर पथ की वक्रता त्रिज्या के समानुपाती होता है।
(A particle is moving in a parabola with uniform angular velocity about the focus. Prove that its normal acceleration at any point is proportional to the radius of curvature of its path at the point.)
[संकेत:परवलय का पदिक समीकरण { p }^{ 2 }=ar लो]
(5.)एक छल्ला जो एक पतली लम्बी चिकनी छड़ पर फिसल सकता है, छड़ के एक सिरे O से दूरी d पर स्थित है।छड़ को एकसमान रूप से बिन्दु O के सापेक्ष एक क्षैतिज तल में घुमाया जाता है।सिद्ध करो कि छल्ला वक्र r=d\cosh { \theta } में घूमता है।
(A ring which can slide on a thin smooth rod rests at a distance d from one end O.The rod is then set revolving uniformly about O in a horizontal plane,Show that in space the ring describes the curve r=d\cosh { \theta } .)
उत्तर-(1)S=\alpha { e }^{ k\psi }+\beta जहां \alpha ,k,\beta अचरांक है।
उपर्युक्त सवालों को हल करने पर त्वरण के त्वरण के स्पर्शरेखीय तथा अभिलाम्बिक घटक (Tangential and normal components of acceleration,Tangential and normal components of velocity and acceleration) को ठीक से समझा जा सकता है।

5.क्या त्वरण वेग के लिए स्पर्शरेखीय है? (Is acceleration tangential to velocity?)-

स्पर्शरेखीय त्वरण की अवधारणा का उपयोग समय में परिवर्तन के साथ एक विशिष्ट त्रिज्या के साथ एक बिंदु के स्पर्शरेखीय वेग में परिवर्तन को मापने के लिए किया जाता है।

6.क्या स्पर्शरेखीय त्वरण हमेशा धनात्मक होता है? (Is tangential acceleration always positive?)-

ध्यान दें कि स्पर्शरेखीय त्वरण या तो धनात्मक या ऋणात्मक हो सकता है,जबकि अभिलाम्बिक या केन्द्रीय त्वरण हमेशा धनात्मक होता है, क्योंकि गुणा \overset { \bullet \bullet }{ s } \theta =\frac { { v }^{ 2 } }{ R } हमेशा धनात्मक होता है (s और θ दोनों में वृद्धि, यदि गति स्पर्शरेखीय इकाई वेक्टर की दिशा,या गति में विपरीत दिशा में होने पर दोनों घट जाती है)।

7.त्वरण का स्पर्शरेखीय घटक क्या है? What is tangential component of acceleration?)-

स्पर्शरेखीय घटक त्वरण का वह भाग है जो वक्र के लिए स्पर्शरेखीय है और अभिलाम्बिक घटक त्वरण का वह भाग है जो वक्र के लिए लम्ब (या ऑर्थोगोनल) है।

8.समतल वक्र पर गतिमान कण का स्पर्शरेखीय‌ और अभिलाम्बिक त्वरण ज्ञात करो (Find the tangential and normal acceleration of a particle moving in a plane curve)-

स्पर्शरेखीय और अभिलाम्बिक घटकों का विचार केवल तब आता है जब कण किसी वक्र के साथ यात्रा कर रहा होता है, क्योंकि वक्र में एक लम्ब और स्पर्शरेखा (समतल) होता है।घूर्णी गति (एक सर्कल में गति) के विशेष मामले में, त्वरण का अभिलाम्बिक घटक v * v / r है और स्पर्शरेखीय घटक 0 है।

9.गतिकी में त्वरण के स्पर्शरेखीय और अभिलाम्बिक घटक (Tangential and normal components of acceleration dynamics)-

स्पर्शरेखीय त्वरण वेग वेक्टर के परिमाण में परिवर्तन की दर का माप है, अर्थात गति और अभीलाम्बिक त्वरण वेग वेक्टर की दिशा के परिवर्तन की दर का एक माप है।
उपर्युक्त प्रश्नों के उत्तर द्वारा त्वरण के स्पर्शरेखीय तथा अभिलाम्बिक घटक (Tangential and normal components of acceleration,Tangential and normal components of velocity and acceleration) को ओर ठीक प्रकार से समझा जा सकता है।

Also Read This Article:-Motion in vertical elastic string

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here