1.प्रतिरोधी माध्यम में सरल रेखीय गति का परिचय (Introduction to Rectilinear Motion in Resisting Medium)-

प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium) का अध्ययन इस आर्टिकल में करेंगे।यदि कोई पिण्ड निर्वात में गति करता है तो उस पर कोई प्रतिरोधी बल कार्य नहीं करता है अर्थात् निर्वात में गति का विरोध नहीं होता है। परन्तु कोई पिण्ड किसी माध्यम जैसे जल,वायु इत्यादि में गति करता है तो उस पर प्रतिरोधी बल लगता है।पिण्ड के वेग बढ़ने के साथ-साथ प्रतिरोधी माध्यम के कारण प्रतिरोध भी बढ़ता जाता है।
सामान्यतः यह प्रतिरोध वेग के समानुपाती होता है।यदि वेग अधिक हो तो प्रतिरोध वेग के वर्ग के समानुपाती होता है तथा वेग ओर भी अधिक हो अर्थात् बहुत अधिक हो तो प्रतिरोध वेग के घन के समानुपाती होता है।
प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium)के इस आर्टिकल में हम प्रतिरोध वेग के समानुपाती के बारे में अध्ययन करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Hooke’s law for elastic string 

2.प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium)-

(1.)वेग के समानुपाती प्रतिरोध के अधीन उर्ध्वाधर गति (Vertical motion under resistance proportional to Velocity)

एक कण विरामावस्था से गुरुत्वाकर्षण बल के अधीन एक ऐसे माध्यम से होकर गिरता है जिसका प्रतिरोध उसके वेग के समानुपाती है।इसकी गति की विवेचना करना
(A particle is moving verically downwards from rest through a medium whose resistance varying as velocity; To discuss its motion)
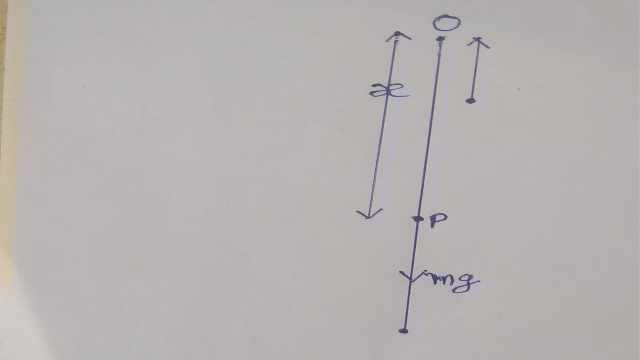
माना कि एक कण बिन्दु O से गुरुत्वाकर्षण के अधीन ऐसे माध्यम में गिरता है जिसका प्रतिरोध वेग के समानुपाती है।
मान लो t समय पर कण की स्थिति P है जहां OP =x तथा P पर कण का वेग v है अब कण पर कार्यशील बल निम्न है-

(i )कण का भार mg उर्ध्वाधर नीचे की ओर

(ii ) प्रतिरोध बल mkv उर्ध्वाधर ऊपर की ओर
अतः समय t पर कण की गति का समीकरण होगा
m\frac { { d }^{ 2 }x }{ { dt }^{ 2 } } =mg-mkv\quadजहां \quad v=\frac { dx }{ dt } \\ \Rightarrow \frac { { d }^{ 2 }x }{ { dt }^{ 2 } } =g-k\frac { dx }{ dt } ......(1)

माना कण का अन्तिम वेग (Terminal Velocity) V है,तब
\ddot { x } =0 तथा v=V
(i) से 0=g-kV\\ \Rightarrow k=\frac { g }{ V }
(i) में k का मान रखने पर

\frac { { d }^{ 2 }x }{ { dt }^{ 2 } } =g-\frac { g }{ V } .v\\ \Rightarrow \frac { dv }{ dt } +\frac { g }{ V } .v=g.....(2)
जो कि रैखिक अवकल समीकरण है जिसका समाकलन-गुणक (I.F.)

{ e }^{ \int { \frac { g }{ V } dt } }={ e }^{ \frac { g }{ V } t }
समाकलन-गुणक से गुणा कर समाकलन करने पर-

v{ e }^{ \frac { g }{ V } t }=g\int { { e }^{ \frac { gt }{ V } } } dt+c\\ v{ e }^{ \frac { g }{ V } t }=V{ e }^{ \frac { gt }{ V } }+c

प्रारम्भ में जब t=0,v=0  \therefore c=-V\\ v{ e }^{ \frac { g }{ V } t }=V{ e }^{ \frac { gt }{ V } }-V\\ \Rightarrow v=V\left[ 1-{ e }^{ -\frac { gt }{ V } } \right] ......(3)
याt=\frac { V }{ g } \log { \left( \frac { V }{ V-v } \right) }

इस समीकरण से कण का वेग t समय पर प्राप्त होता है।अब दोनों पक्षों का समाकलन करने पर-

x=Vt-V\left( -\frac { V }{ g } \right) { e }^{ -\frac { gt }{ V } }+{ c }_{ 1 }
प्रारम्भ में जब t=0,x=0 { c }_{ 1 }=-\frac { { V }^{ 2 } }{ g }

फलत:x=Vt+\frac { { V }^{ 2 } }{ g } \left[ { e }^{ -\frac { gt }{ V } }-1 \right] .......(4)

जिससे कण के द्वारा t समय में गिरी हुई दूरी x प्राप्त होती है।
पुनः (2) से

v\frac { dv }{ dx } +\frac { g }{ V } v=g\\ \Rightarrow v\frac { dv }{ dx } =\frac { g }{ V } \left( V-v \right) \\ \Rightarrow \int { \left( \frac { v }{ V-v } \right) dv } =\int { \frac { g }{ V } } dx\\ \Rightarrow \int { \left( \frac { V }{ V-v } -1 \right) dv } =\int { \frac { g }{ V } } dx\\ \Rightarrow -V\log { \left( V-v \right) } -v=\frac { g }{ V } x+{ c }_{ 2 }

प्रारम्भ में x=0,v=0

\therefore { c }_{ 2 }=-V\log { V } \\ -V\log { \left( V-v \right) } -v=\frac { g }{ V } x-V\log { V } \\ \Rightarrow \frac { gx }{ V } =V\log { V } -V\log { \left( V-v \right) } -v\\ \Rightarrow \frac { gx }{ V } =V\log { \frac { V }{ V-v } } -v\\ \Rightarrow x=\frac { { V }^{ 2 } }{ g } \log { \frac { V }{ V-v } } -\frac { V }{ g } v

उपर्युक्त से प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium) को समझा जा सकता है।

(2.)m द्रव्यमान के एक कण को वेग U से उर्ध्वाधर ऊपर की ओर ऐसे माध्यम में फेंका जाता है जिसका प्रतिरोध वेग के समानुपाती है।इसकी गुरुत्वाकर्षण बल के अधीन गति की विवेचना करना)
(A particle of mass m is projected upwards with velocity U under gravity in a resisting medium due to which resistance varies as the velocity.To discuss the motion,supposing gravitational force to be constant):

माना कि एक कण बिन्दु O से गुरुत्वाकर्षण के अधीन उर्ध्वाधर ऊपर की ओर U वेग से फेंका जाता है जिसका प्रतिरोध वेग के समानुपाती है।
मान लो t समय पर कण की स्थिति P है ,जहां OP =x तथा P पर कण का वेग v है अब कण पर कार्यशील बल निम्न है-

(i )कण का भार mg उर्ध्वाधर नीचे की ओर
(ii ) प्रतिरोध बल mkv उर्ध्वाधर नीचे की ओर
अतः समय t पर कण की गति का समीकरण होगी

m\frac { { d }^{ 2 }x }{ { dt }^{ 2 } } =-mg-mkv\\ \Rightarrow \frac { dv }{ dt } =\frac { { d }^{ 2 }x }{ { dt }^{ 2 } } =-g-kv.....(1)

यदि कण का अन्तिम वेग (Terminal Velocity) V हो तो V=\frac { g }{ k } \\ \therefore -\int { \frac { dv }{ g+kv } } =\int { dt } \\ \Rightarrow -\frac { 1 }{ k } \log { \left( g+kv \right) } =t+{ c }_{ 1 }

गति के प्रारम्भ में t=0,v=U

\therefore { c }_{ 1 }=-\frac { 1 }{ k } \log { \left( g+kU \right) } \\ \Rightarrow t=\frac { 1 }{ k } \log { \left( \frac { g+kU }{ g+kv } \right) } \\ \Rightarrow \frac { g+kU }{ g+kv } { =e }^{ kt }\\ \Rightarrow g+kv=\left( g+kU \right) { e }^{ -kt }\\ \Rightarrow v=-\frac { g }{ k } +\frac { 1 }{ k } \left( g+kU \right) { e }^{ -kt }.....(2)\\ \Rightarrow v=\left( U+V \right) { e }^{ -\frac { gt }{ V } }-V
[जहां अन्तिम V=\frac { g }{ k } वेग है]
इस समीकरण से कण का वेगv, t समय पर प्राप्त होता है।

v=\frac { dx }{ dt } =-\frac { g }{ k } +\frac { 1 }{ k } \left( g+kU \right) { e }^{ -kt }
इसका t के सापेक्ष समाकलन करने पर-

x=-\frac { g }{ k } t-\frac { 1 }{ { k }^{ 2 } } \left( g+kU \right) { e }^{ -kt }+{ c }_{ 2 }
प्रारम्भ में जब t=0,x=0

{ c }_{ 2 }=\frac { 1 }{ { k }^{ 2 } } \left( g+kU \right) \\ \therefore x=-\frac { g }{ k } t+\frac { 1 }{ { k }^{ 2 } } \left( g+kU \right) \left[ 1-{ e }^{ -kt } \right] .....(3)\\ \Rightarrow x=-Vt+\frac { V }{ g } \left( U+V \right) \left( 1-{ e }^{ -\frac { gt }{ V } } \right) .....(4)

इससे t समय पर कण की ऊंचाई x प्राप्त होती है।
पुनः(i) से \frac { { d }^{ 2 }x }{ { dt }^{ 2 } } =-g-kv\\ \Rightarrow v\frac { dv }{ dx } =-g-kv\\ \Rightarrow \int { \frac { -v }{ g+kv } } dv=\int { dx } \\ \Rightarrow -\frac { 1 }{ k } \int { \left( 1-\frac { g }{ g+kv } \right) } dv=\int { dx } \\ \Rightarrow -\frac { v }{ k } +\frac { g }{ { k }^{ 2 } } \log { \left( g+kv \right) } =x+{ c }_{ 2 }

प्रारम्भ में x=0,v=U

\therefore { c }_{ 3 }=\frac { g }{ { k }^{ 2 } } \log { \left( g+kU \right) } -\frac { U }{ K } \\ \therefore x=\frac { g }{ { k }^{ 2 } } \log { \left( \frac { g+kv }{ g+kU } \right) } +\frac { 1 }{ k } \left( U-v \right) \\ \Rightarrow x=\frac { { V }^{ 2 } }{ g } \log { \left( \frac { V+v }{ V+U } \right) } +\frac { V }{ g } \left( U-v \right) .......(5)
यह समीकरण x तथा v का सम्बन्ध बताता है।
यदि कण अधिकतम ऊंचाई H तक जाता है तो
अधिकतम ऊंचाई पर v=0

\therefore H=\frac { g }{ { k }^{ 2 } } \log { \left( \frac { g }{ g+kU } \right) } +\frac { U }{ k }
अब k=\frac { g }{ V } रखने पर 

H=\frac { UV }{ g } +\frac { { V }^{ 2 } }{ g } \log { \left( \frac { V }{ V+U } \right) }

अधिकतम ऊंचाई H तक का उड्डयन काल (Time of flight T for the greatest height H )
(2) में v=0 तथा t=T रखने पर (जो H ऊंचाई तक उड्डयन काल है)

0=-\frac { g }{ k } +\frac { 1 }{ k } \left( g+kU \right) { e }^{ -kT }\\ \Rightarrow { e }^{ kT }=\frac { g+kU }{ g } \\ \Rightarrow T=\frac { 1 }{ k } \log { \left( 1+\frac { kU }{ g } \right) }
अबk=\frac { g }{ V } रखने पर 

T=\frac { V }{ g } \log { \left( 1+\frac { U }{ V } \right) } .....(6)

उपर्युक्त उदाहरण से प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium) को समझा जा सकता है।

3.प्रतिरोधी माध्यम में सरल रेखीय गति से सम्बन्धित सवाल(Questions related to simple linear motion in resistive medium)–

प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium) को समझने के लिए कुछ उदाहरण लेते है –

Question-1.एक कण को चिकने क्षैतिज तल पर ऐसे माध्यम में u वेग से फेंका जाता है जिसका प्रतिरोध प्रति इकाई संहति के लिए वेग का k गुणा है।सिद्ध कीजिए कि t समय पश्चात् यदि इसका वेग v तथा इसके द्वारा s दूरी तय की जाती हो तो
(A particle is projected with Velocity u along a smooth horizontal plane in a medium whose resistance per unit mass k times the velocity. prove that the Velocity v after a time t and the distance s in that time are given by)

v=u{ e }^{ -kt }\quad ,s=\frac { u }{ k } \left( 1-{ e }^{ -kt } \right)

Solution-चिकने क्षैतिज तल पर किसी समय गति का समीकरण-

m\frac { { d }^{ 2 }x }{ { dt }^{ 2 } } =-mkv\\ \Rightarrow \frac { { d }^{ 2 }x }{ { dt }^{ 2 } } =-kv\\ \Rightarrow \frac { dv }{ dt } =-kv\\ \Rightarrow -\frac { dv }{ kv } =dt
समाकलन करने पर-

-\int { \frac { dv }{ kv } } =\int { dt } \\ -\frac { 1 }{ k } \log { v } =t+{ c }_{ 1 }
प्रारम्भ में t=0,v=u

\therefore { c }_{ 1 }=-\frac { 1 }{ k } \log { u } \\ -\frac { 1 }{ k } \log { v } =t-\frac { 1 }{ k } \log { u } \\ \Rightarrow \frac { 1 }{ k } \log { u } -\frac { 1 }{ k } \log { v } =t\\ \Rightarrow -\frac { 1 }{ k } \left( \log { v } -\log { u } \right) =t\\ \Rightarrow \log { \frac { v }{ u } } =-kt\\ \Rightarrow v=u.{ e }^{ -kt }\\ \frac { ds }{ dt } =u.{ e }^{ -kt }\\ \int { ds } =\int { u.{ e }^{ -kt } } dt\\ s=-\frac { u }{ k } { e }^{ -kt }+{ c }_{ 2 }

जब t=0, तो s=0

\therefore { c }_{ 2 }=\frac { u }{ k } \\ s=-\frac { u }{ k } { e }^{ -kt }+\frac { u }{ k } \\ s=\frac { u }{ k } \left( 1-{ e }^{ -kt } \right) \quad \quad ,v=u{ e }^{ -kt }

उपर्युक्त उदाहरण से प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium) को समझा जा सकता है।
Question-2.इकाई संहति का एक कण V वेग से उर्ध्वाधर दिशा में ऊपर की ओर एक ऐसे माध्यम में फेंका जाता जिसका प्रतिरोध kv है।सिद्ध करो कि कण प्रक्षेप बिन्दु पर U वेग से लौटकर आएगा जहां
(A particle of unit mass is projected vertically upwards with velocity V in a medium whose resistance is kv. prove that the particle will return to the point of projection with Velocity U , where

U+V=\frac { g }{ k } \log { \left( \frac { g+kV }{ g-kU } \right) }
Solution-नीचे की ओर गुरुत्वाकर्षण के अधीन गिरते हुए कण की गति का समीकरण-

m\frac { { d }^{ 2 }x }{ { dt }^{ 2 } } =mg-mkv\\ \Rightarrow \frac { { d }^{ 2 }x }{ { dt }^{ 2 } } =g-kv\\ \Rightarrow v\frac { dv }{ dx } =g-kv\\ \Rightarrow v\frac { dv }{ g-kv } =dx
समाकलन करने पर-

\Rightarrow \int { v\frac { dv }{ g-kv } } =\int { dx } \\ \Rightarrow \int { \left[ -\frac { dv }{ k } +\frac { g }{ k } .\frac { dv }{ g-kv } \right] } =\int { dx } \\ \Rightarrow -\int { \frac { dv }{ k } } +\frac { g }{ k } \int { \frac { dv }{ g-kv } } =\int { dx } \\ \Rightarrow -\frac { v }{ k } -\frac { g }{ { k }^{ 2 } } \log { \left( g-kv \right) } =x+{ c }_{ 1 }

प्रारम्भ में v=0,x=0

\therefore { c }_{ 1 }=-\frac { g }{ { k }^{ 2 } } \log { \left( g \right) } \\ \Rightarrow -\frac { v }{ k } -\frac { g }{ { k }^{ 2 } } \log { \left( g-kv \right) } =x-\frac { g }{ { k }^{ 2 } } \log { \left( g \right) } \\ \Rightarrow -\frac { v }{ k } +\frac { g }{ { k }^{ 2 } } \log { \left( g \right) } -\frac { g }{ { k }^{ 2 } } \log { \left( g-kv \right) } =x\\ \Rightarrow -\frac { v }{ k } +\frac { g }{ { k }^{ 2 } } \log { \left( \frac { g }{ g-kv } \right) } =x
प्रक्षेप बिन्दु पर x=h,v=U

\Rightarrow -\frac { U }{ k } +\frac { g }{ { k }^{ 2 } } \log { \left( \frac { g }{ g-kU } \right) } =h.......(1)

जब कण को ऊपर की ओर फेंका जाता है तो कण की गति का समीकरण-

m\frac { { d }^{ 2 }y }{ { dt }^{ 2 } } =-mg-mkv\\ \Rightarrow \frac { { d }^{ 2 }y }{ { dt }^{ 2 } } =-\left( g+kv \right) \\ \Rightarrow v\frac { dv }{ dy } =-\left( g+kv \right) \\ -\frac { vdv }{ g+kv } =dy

समाकलन करने पर-

\Rightarrow -\int { \frac { vdv }{ g+kv } } =\int { dy } \\ \Rightarrow -\int { \left[ \frac { 1 }{ k } -\frac { g }{ k } .\frac { 1 }{ g+kv } \right] dv } =\int { dy } \\ \Rightarrow -\int { \frac { dv }{ k } } +\frac { g }{ k } \int { \frac { dv }{ g+kv } } =\int { dy } \\ \Rightarrow -\frac { v }{ k } +\frac { g }{ { k }^{ 2 } } \log { \left( g+kv \right) = } y+{ c }_{ 2 }
प्रारम्भ में v=V,y=0

\therefore { c }_{ 2 }=-\frac { V }{ k } +\frac { g }{ { k }^{ 2 } } \log { \left( g+kV \right) } \\ \Rightarrow -\frac { v }{ k } +\frac { g }{ { k }^{ 2 } } \log { \left( g+kv \right) = } y-\frac { V }{ k } +\frac { g }{ { k }^{ 2 } } \log { \left( g+kV \right) } \\ \Rightarrow y=\frac { V-v }{ k } +\frac { g }{ { k }^{ 2 } } \log { \left( \frac { g+kv }{ g+kV } \right) }
जब y=h,v=0

\Rightarrow h=\frac { V }{ k } +\frac { g }{ { k }^{ 2 } } \log { \left( \frac { g }{ g+kV } \right) } .......(2)

समीकरण (1) व (2) से-

\frac { V }{ k } +\frac { g }{ { k }^{ 2 } } \log { \left( \frac { g }{ g+kV } \right) } =-\frac { U }{ k } +\frac { g }{ { k }^{ 2 } } \log { \left( \frac { g }{ g-kU } \right) } \\ \Rightarrow \frac { V+U }{ k } +\frac { g }{ { k }^{ 2 } } \log { \left( \frac { g-kU }{ g+kV } \right) } =0\\ V+U=\frac { g }{ k } \log { \left( \frac { g+kV }{ g-kU } \right) }

उपर्युक्त उदाहरण से प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium) को समझा जा सकता है।

Question-3.एक भारी कण उर्ध्वाधर दिशा में ऊपर की ओर ऐसे माध्यम में फेंका जाता है कि जिसका किसी बिन्दु पर कण का वेग क्रमशः { v }_{ 1 }\quad तथा \quad { v }_{ 2 } ऊपर जाते तथा नीचे आते समय हो तथा बिन्दु से गुजरने में समय अन्तराल t हो ,यदि V कण का अन्तिम वेग है तो सिद्ध कीजिए
{ v }_{ 1 }+{ v }_{ 2 }=gt\quad तथा \quad V-{ v }_{ 2 }=\left( V+{ v }_{ 1 } \right) { e }^{ -\frac { gt }{ V } }

(A particle is projected vertically in a rasisting medium, the rasistance varying as the velocity.If{ v }_{ 1 }\quad and \quad { v }_{ 2 }  are its Velocities at any point in its upwards and downward path and t the interval between its passage through this point,if V be the terminal Velocity: prove that{ v }_{ 1 }+{ v }_{ 2 }=gt\quad and \quad V-{ v }_{ 2 }=\left( V+{ v }_{ 1 } \right) { e }^{ -\frac { gt }{ V } }
Solution-कण के ऊपर जाते समय गुरुत्वाकर्षण बल के अधीन गति का समीकरण

m\frac { { d }^{ 2 }x }{ { dt }^{ 2 } } =-mg-\frac { mgv }{ V } \\ \Rightarrow \frac { { d }^{ 2 }x }{ { dt }^{ 2 } } =-g\left( \frac { V+v }{ V } \right) ....(1)\\ \Rightarrow \frac { dv }{ dt } =-\frac { g }{ V } \left( V+v \right)

(जहां V अन्तिम वेग है)
समाकलन करने पर-

\Rightarrow -\frac { V }{ g } \int { \frac { dv }{ V+v } } =\int { dt } \\ \Rightarrow -\frac { V }{ g } \log { \left( V+v \right) } =t+{ c }_{ 1 }

आरम्भ मेंv={ v }_{ 1 },t=0\\ { c }_{ 1 }=-\frac { V }{ g } \log { \left( V+{ v }_{ 1 } \right) } \\ \Rightarrow -\frac { V }{ g } \log { \left( V+v \right) } =t-\frac { V }{ g } \log { \left( V+{ v }_{ 1 } \right) } \\ \Rightarrow \frac { V }{ g } \log { \left( \frac { V+{ v }_{ 1 } }{ V+v } \right) } =t
उच्चत्तम बिन्दु परv=0,t={ t }_{ 1 }\\ \Rightarrow \frac { V }{ g } \log { \left( \frac { V+{ v }_{ 1 } }{ V } \right) } ={ t }_{ 1 }......(2)
पुनः समीकरण (1) से

v\frac { dv }{ dx } =-\frac { g\left( V+v \right) }{ V } \\ \Rightarrow -\frac { Vvdv }{ g\left( V+v \right) } =dx
समाकलन करने पर-

\Rightarrow -\int { \frac { Vvdv }{ g\left( V+v \right) } } =\int { dx } \\ \Rightarrow -\frac { V }{ g } \int { \left( 1-\frac { V }{ V+v } \right) } dv=\int { dx } \\ \Rightarrow -\frac { V }{ g } \int { dv } +\frac { { V }^{ 2 } }{ g } \int { \frac { 1 }{ V+v } } dv=\int { dx } \\ \Rightarrow -\frac { Vv }{ g } +\frac { { V }^{ 2 } }{ g } \log { \left( V+v \right) } =x+{ c }_{ 2 }

प्रारम्भ में जब v={ v }_{ 1 }\quad तो \quad x=0\\ { c }_{ 2 }=\frac { { V }^{ 2 } }{ g } \log { \left( V+{ v }_{ 1 } \right) } -\frac { V{ v }_{ 1 } }{ g } \\ \Rightarrow -\frac { Vv }{ g } +\frac { { V }^{ 2 } }{ g } \log { \left( V+v \right) } =x+\frac { { V }^{ 2 } }{ g } \log { \left( V+{ v }_{ 1 } \right) } -\frac { V{ v }_{ 1 } }{ g } \\ \Rightarrow \frac { V{ v }_{ 1 } }{ g } -\frac { Vv }{ g } +\frac { { V }^{ 2 } }{ g } \log { \left( \frac { V+v }{ V+{ v }_{ 1 } } \right) } =x

जब v=0 तब x=h

\Rightarrow \frac { V{ v }_{ 1 } }{ g } +\frac { { V }^{ 2 } }{ g } \log { \left( \frac { V }{ V+{ v }_{ 1 } } \right) } =h.....(3) 

पुनः कण की गुरुत्वाकर्षण बल के अधीन गिरते समय गति का समीकरण-

m\frac { { d }^{ 2 }x }{ { dt }^{ 2 } } =mg-\frac { mgv }{ V } (जहां V अन्तिम वेग है)

\Rightarrow \frac { { d }^{ 2 }x }{ { dt }^{ 2 } } =g-\frac { gv }{ V } ......(4)\\ \Rightarrow \frac { dv }{ dt } =\frac { g }{ V } \left( V-v \right) \\ \Rightarrow \frac { Vdv }{ g\left( V-v \right) } =dt

समाकलन करने पर-

\Rightarrow \frac { V }{ g } \int { \frac { dv }{ V-v } } =\int { dt } \\ \Rightarrow -\frac { V }{ g } \log { \left( V-v \right) =t+ } { c }_{ 3 }

जब t=0 तो v=0

\therefore { c }_{ 3 }=-\frac { V }{ g } \log { V } \\ -\frac { V }{ g } \log { \left( V-v \right) } =t-\frac { V }{ g } \log { V } \\ \Rightarrow \frac { V }{ g } \log { \left( \frac { V }{ V-v } \right) } =t

जबt={ t }_{ 2 },v={ v }_{ 2 }\\ \Rightarrow \frac { V }{ g } \log { \left( \frac { V }{ V-{ v }_{ 2 } } \right) } ={ t }_{ 2 }.......(5)

पुनः समीकरण (4)से-

v\frac { dv }{ dy } =g-\frac { gv }{ V } \\ \Rightarrow v\frac { dv }{ dy } =\frac { g }{ V } \left( V-v \right) \\ \Rightarrow \frac { Vvdv }{ g\left( V-v \right) } =dy
समाकलन करने पर-

\Rightarrow \frac { V }{ g } \int { \left[ \frac { V }{ V-v } -1 \right] dv } =\int { dy } \\ \Rightarrow \frac { V }{ g } \int { \frac { V }{ V-v } dv } -\frac { V }{ g } \int { dv } =\int { dy } \\ \Rightarrow -\frac { { V }^{ 2 } }{ g } \log { \left( V-v \right) } -\frac { Vv }{ g } =y+{ c }_{ 4 }
जब v=0 तो y=0

{ c }_{ 4 }=-\frac { { V }^{ 2 } }{ g } \log { V } \\ \Rightarrow -\frac { { V }^{ 2 } }{ g } \log { \left( V-v \right) } -\frac { Vv }{ g } =y-\frac { { V }^{ 2 } }{ g } \log { V } \\ \Rightarrow \frac { { V }^{ 2 } }{ g } \log { \left( \frac { V }{ V-v } \right) } -\frac { Vv }{ g } =y

जब v={ v }_{ 2 }\quad तो \quad y=h\\ \Rightarrow \frac { { V }^{ 2 } }{ g } \log { \left( \frac { V }{ V-{ v }_{ 2 } } \right) } -\frac { V{ v }_{ 2 } }{ g } =h....(6)
समीकरण (5) व (2) को जोड़ने पर-

\Rightarrow \frac { V }{ g } \log { \left( \frac { V }{ V-{ v }_{ 2 } } \right) } +\frac { v }{ g } \log { \left( \frac { V+{ v }_{ 1 } }{ V } \right) } ={ t }_{ 2 }+{ t }_{ 1 }\\ \Rightarrow \frac { V }{ g } \left[ \log { \left( \frac { V }{ V-{ v }_{ 2 } } \right) } +\log { \left( \frac { V+{ v }_{ 1 } }{ V } \right) } \right] =t\\ \Rightarrow \log { \left( \frac { V+{ v }_{ 1 } }{ V-{ v }_{ 2 } } \right) } =\frac { gt }{ V } ......(7)\\ \Rightarrow \log { \left( \frac { V-{ v }_{ 2 } }{ V+{ v }_{ 1 } } \right) } =-\frac { gt }{ V } \\ \Rightarrow V-{ v }_{ 2 }=\left( V+{ v }_{ 1 } \right) { e }^{ -\frac { gt }{ V } }

समीकरण (3) व (6) से-

\Rightarrow \frac { { V }^{ 2 } }{ g } \log { \left( \frac { V }{ V-{ v }_{ 2 } } \right) } -\frac { V{ v }_{ 2 } }{ g } =\frac { V{ v }_{ 1 } }{ g } +\frac { { V }^{ 2 } }{ g } \log { \left( \frac { V }{ V+{ v }_{ 1 } } \right) } \\ \Rightarrow \frac { V{ v }_{ 1 } }{ g } +\frac { V{ v }_{ 2 } }{ g } =\frac { { V }^{ 2 } }{ g } \log { \left( \frac { V+{ v }_{ 1 } }{ V-{ v }_{ 2 } } \right) } \\ \Rightarrow \frac { V }{ g } \left( { v }_{ 1 }+{ v }_{ 2 } \right) =\frac { { V }^{ 2 } }{ g } \log { \left( \frac { V+{ v }_{ 1 } }{ V-{ v }_{ 2 } } \right) } \\ \Rightarrow \left( { v }_{ 1 }+{ v }_{ 2 } \right) =V\log { \left( \frac { V+{ v }_{ 1 } }{ V-{ v }_{ 2 } } \right) } .....(8)

समीकरण (7) व(8) से-

{ v }_{ 1 }+{ v }_{ 2 }=V.\frac { gt }{ V } \\ { v }_{ 1 }+{ v }_{ 2 }=gt\quad ,\quad V-{ v }_{ 2 }=\left( V+{ v }_{ 1 } \right) { e }^{ -\frac { gt }{ V } }

उपर्युक्त उदाहरणों से प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium) को समझा जा सकता है।

प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium) के कुछ सवाल आप अपने स्तर पर करे ताकि प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium) आपको अच्छे से समझ आ सके |

Also Read This Article:-Radial and Transverse velocities and Accelerations

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Twitter	click here
4.	Instagram	click here
5.	Linkedin	click here
6.	Facebook Page	click here