Right Circular Cylinder
लम्ब्वृत्तीय बेलन(Right circular cylinder):
- लम्ब्वृत्तीय बेलन(Right circular cylinder) में बेलन वह पृष्ठ है जो ऐसी चर सरल रेखा द्वारा जनित होता है जो एक निश्चित सरल रेखा के समान्तर रहती है तथा दिए हुए वक्र को प्रतिच्छेदित करती है या स्पर्श करती है।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:Cylinder
(1.)लम्ब्वृत्तीय बेलन(Right circular cylinder)
- लम्ब्वृत्तीय बेलन वह ठोस आकृति है जिसमें एक पृष्ठ और सर्वांगसम वृत्तीय अनुप्रस्थ काट हो तथा बेलन का अक्ष वृत्तीय अनुप्रस्थ काट पर लम्बवत हो।बेलन का अक्ष वृत्तीय अनुप्रस्थ काटों के केंद्रों को मिलाने वाली रेखा होती है।अक्ष के समांतर और पार्श्व पृष्ठ पर स्थित रेखा जनक कहलाती है।चित्र में रेखाएं AB,CD जनक हैं।बेलन के नीचे के वृत्तीय सिरे को आधार रेखाखंड AB को ऊँचाई तथा वृत्तीय सिरे की त्रिज्या OA कहते हैं।ठोस बेलन के दोनो सिरे बंद होते हैं।
Figure-Right Circular Cylinder
- अत: हम कह सकते हैं जब किसी आयत OABO’ की भुजा OO’ को अक्ष मानकर चारों ओर परिक्रमण कराते हैं तो एक ठोस बेलन प्राप्त होता है जिसकी ऊँचाई AB तथा त्रिज्या OA के बराबर होती है।यदि बेलन की त्रिज्या r और ऊँचाई h हो तो बेलन के (i)प्रत्येक सिरे या आधार का क्षेत्रफल =\pi {r^{2}}
(ii)बेलन के वक्र पृष्ठ का क्षेत्रफल=आयत OABO’ का क्षेत्रफल
बेलन के वक्र पृष्ठ का क्षेत्रफल= 2\pi r × h=2\pi rh वर्गइकाई (iii)अत:बेलन का सम्पूर्ण
पृष्ठीय क्षेत्रफल=2\pi rh+2\pi{r^{2}} =2\pi r(h+r)
(iV)बेलन का आयतन=आधार का क्षेत्रफल x ऊँचाई= \pi{r^{2}} × h=\pi{r^{2}} h घन इकाई
(2.)खोखला बेलन (Hollow Cylinder):
खोखला बेलन वह आकृति है जो कि दो बेलनों से मिलकर बनती हो।जिनकी ऊँचाई समान और त्रिज्या असमान हों।खोखले
बेलन के दोंनों सिरे खुले होते हैं।
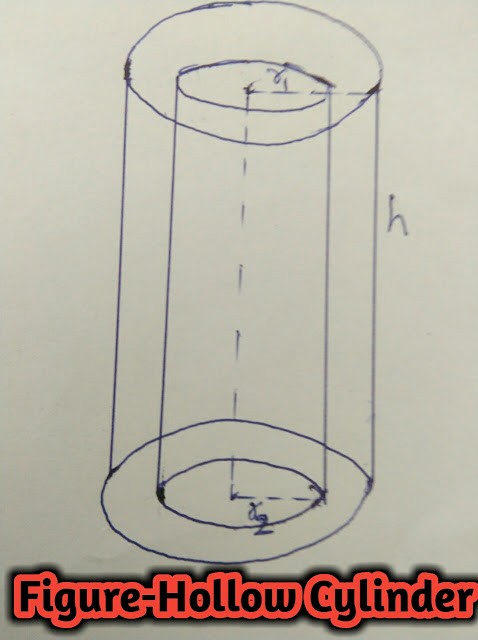
Figure-Hollow Cylinder
- यदि r_{1}\text{ और }r_{2} खोख्ले बेलन की बाह्य और अंत: त्रिज्या तथा ऊँचाई h हो तो
(i)प्रत्येक सिरे का क्षेत्रफल= \pi(r_{1}^{2} -r_{2}^{2})
(ii)वक्र पृष्ठ का क्षेत्रफल=बाह्य पृष्ठ का क्षेत्रफल+अंत: पृष्ठ का क्षेत्रफल=2\pi r_{1} h+2\pi r_{2}h
वक्र पृष्ठ का क्षेत्रफल= 2\pi h(r_{1} +r_{2})
(iii)अत: खोखले बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल=वक्र पृष्ठ का क्षेत्रफल+2(एक सिरे का क्षेत्रफल)=
2\pi(r_{1} +r_{2} )h+2\pi (r_{1} ^{2}-r_{2}^{2})=2\pi (r_{1}+r_{2})+ 2\pi (r_{1}+r_{2})(r_{1}-r_{2}) - खोखले बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल=2\pi (r_{1}+r_{2})(h+r_{1}-r_{2})
(iv)खोखले बेलन का आयतन=बाह्य बेलन का आयतन-अन्त: बेलन का आयतन
= \pi r_{1}^2 h-r_{2}^{2}\pi h
खोखले बेलन का आयतन= \pi(r_{1}^{2}-r_{2}^{2}) - (3.) Example:
प्रश्न:-दो लम्बवृत्तीय बेलनों की त्रिज्याओं का अनुपात 2:3 तथा ऊँचाईयों का अनुपात 5:4 है तो दोनों बेलनों के वक्र पृष्ठीय क्षेत्रफलों
तथा आयतनों का अनुपात ज्ञात कीजिए।
उत्तर:माना पहले बेलन की त्रिज्या r_{1}=2x दूसरे बेलन की त्रिज्या r_{2}=3x
पहले बेलन की ऊँचाई h_{1}=5y दूसरे बेलन की त्रिज्या h_{2}=4y
पहले बेलन का वक्र पृष्ठ का क्षेत्रफल S_{1}=2\pi r_{1} h_{1}=2\pi (2x)(5y)=20\pi xy - दूसरे बेलन का वक्र पृष्ठ का क्षेत्रफल S_{2}=2\pi r_{2} h_{2}=2 \pi (3x)(4y)=24\pi xy
दोनों बेलनों के वक्र पृष्ठों में अनुपात S_{1}:S_{2}
= 20\pi x y:24 \pi xy=5:6
पहले बेलन का आयतन V_{1}= \pi r_{1} ^{2}h=\pi (2x)(2x)(5y)=20\pi xy
दूसरे बेलन का आयतन=V _{2}=\pi r_{2}^{2}h=\pi(3x)(3x)(4y)=36\pi xy दोनों बेलनों के आयतनों
में अनुपात V_{1}:V_{2}=20\pi x y: 36\pi x y=5:9 - उपर्युक्त आर्टिकल में लम्ब्वृत्तीय बेलन(Right circular cylinder) के बारे में बताया गया है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |