Area of quadrilateral in hindi
चतुर्भुजों का क्षेत्रफल(Area of Quadrilateral):-
(1.)चक्रीयचतुर्भुज का क्षेत्रफल(cyclic quadrilateral) :-
ऐसा चतुर्भुज जिसके चारों शीर्ष वृत्त की परिधि पर स्थित हों,चक्रीय चतुर्भुज कहलाता है।चक्रीय चतुर्भुज के सम्मुख कोण सम्पूरक होते हैं।चित्रानुसार एक चक्रीय चतुर्भुज
ABCD है जिसकी भुजाएँ क्रमश: a,b,c एवं dहै। अत: अर्द्ध परिमाप s=(a+b+c+d)/2 है।
ABCD है जिसकी भुजाएँ क्रमश: a,b,c एवं dहै। अत: अर्द्ध परिमाप s=(a+b+c+d)/2 है।
अत: चक्रीय चतुर्भुज
का क्षेत्रफल =√(s-a)(s-b)(s-c)(s-d)
 |
cyclic quadrilateral |
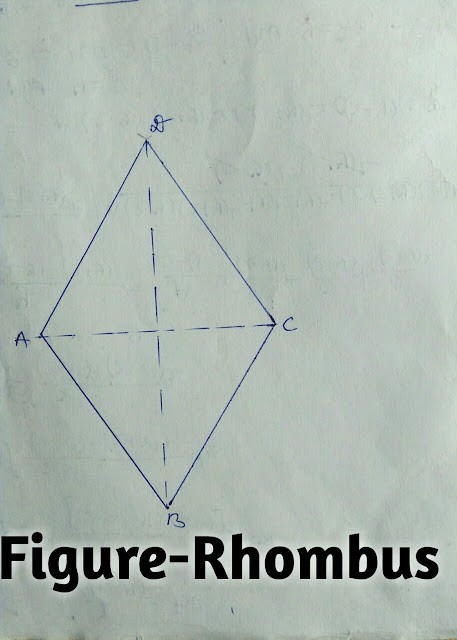
(2.)समचतुर्भुज(Rhombus) का क्षेत्रफल:-
ऐसा समांतर चतुर्भुज जिसकी चारों भुजाएँ समान हो एवं जिसके विकर्ण परस्पर
समकोण पर समद्विभाजित होते हो,समचतुर्भुज कहलाता है।
समकोण पर समद्विभाजित होते हो,समचतुर्भुज कहलाता है।
समचतुर्भुज का क्षेत्रफल=(1/2) x विकर्णों का गुणंफल
 |
| Figure-Rhombus |
(3.)समलम्ब
चतुर्भुज(Trapezium quadrilateral) का क्षेत्रफल:-
ऐसा चतुर्भुज जिसकी केवल दो भुजाएँ समांतर हो समलम्ब चतुर्भुज
कहलाता है। चित्रानुसारABCD एक समलम्ब चतुर्भुज है। जिसकी भुजाएँAB एवं CDसमांतर हैं एवं दोनों समांतर भुजाओं के मध्य दूरी
DE है।यहाँ DE भुजा AB पर लम्ब है तथा DB विकर्ण है।
कहलाता है। चित्रानुसारABCD एक समलम्ब चतुर्भुज है। जिसकी भुजाएँAB एवं CDसमांतर हैं एवं दोनों समांतर भुजाओं के मध्य दूरी
DE है।यहाँ DE भुजा AB पर लम्ब है तथा DB विकर्ण है।
समलम्ब चतुर्भुज
ABCD का क्षेत्रफल=त्रिभुज
ABD का क्षेत्रफल + त्रिभुज BCD का क्षेत्रफल
ABCD का क्षेत्रफल=त्रिभुज
ABD का क्षेत्रफल + त्रिभुज BCD का क्षेत्रफल
अर्थात` समलम्ब चतुर्भुज का क्षेत्रफल=(1/2)
x समांतर भुजाओं का योग x
समांतर भुजओं के मध्य दूरी
(4.)समांतर
चतुर्भुज(Parallelogram) का क्षेत्रफल :-
ऐसा चतुर्भुज जिसकी आमने सामने की भुजाएँ समान्तर या बराबर हो।
समांतर चतुर्भुज
का क्षेत्रफल=आधार का क्षेत्रफल x ऊँचाई
 |
Figure-Parallelogram |
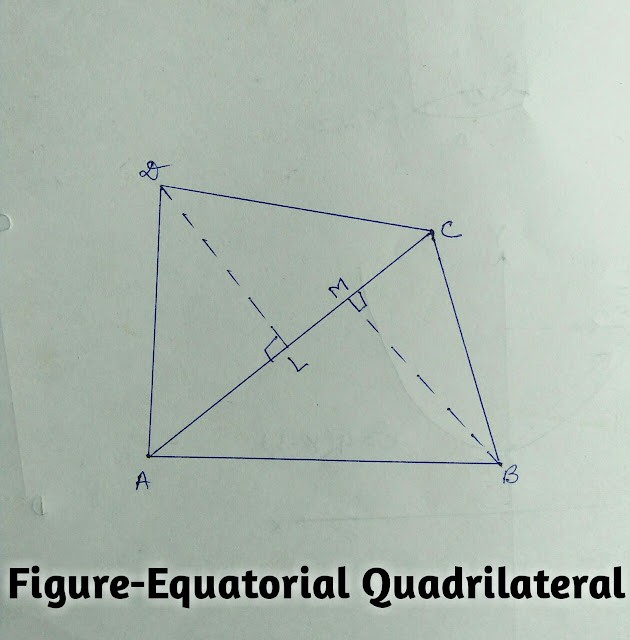
(5.)विषमबाहु
चतुर्भुज:(Equatorial quadrilateral):-
विषमबाहु चतुर्भुज
का क्षेत्रफल=(1/2)x विकर्ण x विकर्ण पर डाले गए लम्बों का योग
प्रश्न:-एक चक्रीय
चतुर्भुजाकार मैदान की भुजाएँ क्रमश: 72 मीटर,154 मीटर’80 मीटर एवं 150 मीटर है। इसका
क्षेत्रफल ज्ञात कीजिए। इस मैदान में टाइल बिछवाने का व्यय 5 रुपये प्रति वर्ग मीटर
हो तो कुल व्यय ज्ञात कीजिए।
चतुर्भुजाकार मैदान की भुजाएँ क्रमश: 72 मीटर,154 मीटर’80 मीटर एवं 150 मीटर है। इसका
क्षेत्रफल ज्ञात कीजिए। इस मैदान में टाइल बिछवाने का व्यय 5 रुपये प्रति वर्ग मीटर
हो तो कुल व्यय ज्ञात कीजिए।
उत्तर-माना a= 72 मीटर,b=154
मीटर’ c=80 मीटर एवं d= 150 मीटर
मीटर’ c=80 मीटर एवं d= 150 मीटर
अर्द्ध परिमाप s=(a+b+c+d)/2=(72+154+80+150)/2=456/2=228
अत: चक्रीय चतुर्भुज
का क्षेत्रफल =√(s-a)(s-b)(s-c)(s-d)=√(228-72)(228-154)(228-80)(228-150)
का क्षेत्रफल =√(s-a)(s-b)(s-c)(s-d)=√(228-72)(228-154)(228-80)(228-150)
=√(156
x 74 x 148 x 78)=√(2 x2 x3 x13 x2 x37 x 2 x 2 x 37 x 2 x3 x13)=2 x 2 x 2 x
3 x13 x37=11544
x 74 x 148 x 78)=√(2 x2 x3 x13 x2 x37 x 2 x 2 x 37 x 2 x3 x13)=2 x 2 x 2 x
3 x13 x37=11544
मैदान में टाइल बिछवाने
का व्यय= 11544 x 5=57720
का व्यय= 11544 x 5=57720
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
