1.गोले के सापेक्ष ध्रुव एवं ध्रुवीय समतल (Pole and Polar plane respect to sphere)-

 गोले के सापेक्ष ध्रुव एवं ध्रुवीय  समतल (Pole and Polar plane respect to sphere) के बारे मे अध्ययन करेंगे |

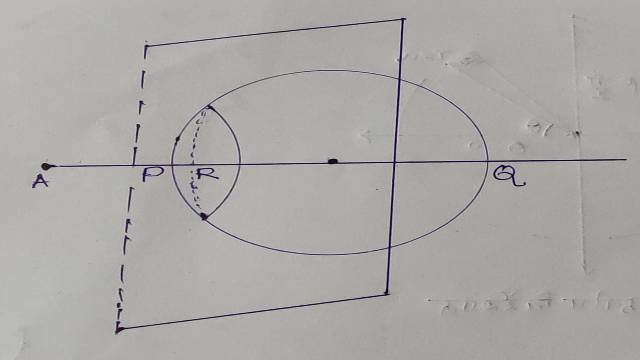
यदि एक स्थिर बिन्दु A से गुजरने वाली एक चर रेखा किसी गोले को P तथा Q बिन्दुओं पर काटती है तथा इस रेखा पर R एक ऐसा बिन्दु है कि AP,AR तथा AQ हरात्मक श्रेणी (H.P.) में हो अर्थात्

AP=\frac { (2AP.AQ) }{ (AP+AQ) }
तो R का बिन्दुपथ (Locus) एक समतल होगा जो बिन्दु A का गोले के सापेक्ष ध्रुवीय समतल (Polar plane) कहलाता है।A ध्रुवीय समतल का ध्रुव (Pole) कहलाता है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Diameter form of equation of sphere

2.गोले के सापेक्ष ध्रुवीय समतल का समीकरण ज्ञात करना (Finding equation of polar plane respect to sphere)-

बिन्दु A(\alpha ,\beta ,\gamma ) का गोले { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2ux+2vy+2wz+d=0 के सापेक्ष ध्रुवीय समतल का समीकरण ज्ञात करना।
(To find the polar plane of the pointA(\alpha ,\beta ,\gamma ) with repect to the sphere{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }+2ux+2vy+2wz+d=0 )
मान लो बिन्दु A(\alpha ,\beta ,\gamma ) से गुजरने वाली रेखा के समीकरण हैं

\frac { x-\alpha }{ l } =\frac { y-\beta \quad }{ m } =\frac { z-\gamma }{ n } =r

जहां l,m,n रेखा के दिक्अनुपात है।इस रेखा पर स्थित किसी बिन्दु के निर्देशांक हैं:

(\alpha +lr,\beta +mr,\gamma +nr)
यदि यह बिन्दु दिए हुए गोले एवं रेखा (1) का प्रतिच्छेदन बिन्दु हो तो

{ (\alpha +lr) }^{ 2 }+{ (\beta +mr) }^{ 2 }+{ (\gamma +nr) }^{ 2 }+2u{ (\alpha +lr) }+2v{ (\beta +mr) }+2w{ (\gamma +nr) }+d=0\\ \Rightarrow { r }^{ 2 }+2[l{ (\alpha +u) }+m{ (\beta +v) }+n{ (\gamma +w) }]r+({ \alpha }^{ 2 }+{ \beta }^{ 2 }+{ \gamma }^{ 2 }+2u\alpha +2v\beta +2w\gamma +d)=0…(2)
समीकरण (2),r में द्विघात (quadratic) समीकरण है अतः इससे r के दो मान प्राप्त होंगे।मान लो ये मान { r }_{ 1 } तथा { r }_{ 2 }है।इन मानों के संगत रेखा एवं गोले के प्रतिच्छेदन बिन्दु P और Q प्राप्त होंगे अर्थात् AP={ r }_{ 1 } तथा AQ={ r }_{ 2 }\\ { r }_{ 1 }+{ r }_{ 2 }=AP+AQ\\ =-2[l(\alpha +u)+m(\beta +v)+n(\gamma +w)]
तथा { r }_{ 1 }.{ r }_{ 2 }=AP.AQ\\ \qquad ={ \alpha }^{ 2 }+{ \beta }^{ 2 }+{ \gamma }^{ 2 }+2u\alpha +2v\beta +2w\gamma +d
यदि रेखा APQ पर R एक ऐसा बिन्दु हो कि AR=r,तब

AR=\frac { (2AP.AQ) }{ (AP+AQ) } \Rightarrow r=\frac { 2{ r }_{ 1 }{ r }_{ 2 } }{ { r }_{ 1 }+{ r }_{ 2 } } \\ \Rightarrow r=\frac { 2({ \alpha }^{ 2 }+{ \beta }^{ 2 }+{ \gamma }^{ 2 }+2u\alpha +2v\beta +2w\gamma +d) }{ -2[l(\alpha +u)+m(\beta +v)+n(\gamma +w)] } \\ \Rightarrow 2[u{ (\alpha +lr) }+v{ (\beta +mr) }+w{ (\gamma +nr) }]r+({ \alpha }^{ 2 }+{ \beta }^{ 2 }+{ \gamma }^{ 2 }+2u\alpha +2v\beta +2w\gamma +d)=0…..(3)
अब यदि R के निर्देशांक (x,y,z) हों तो R रेखा (1) पर स्थित होने से,

x={ (\alpha +lr) },y={ (\beta +mr) },z={ (\gamma +nr) }
r का मान इनसे (3) में रखने पर R का बिन्दुपथ होगा

(x-\alpha ).(\alpha +u)+(y-\beta ).(\beta +v)+(z-\gamma ).(\gamma +w)+({ \alpha }^{ 2 }+{ \beta }^{ 2 }+{ \gamma }^{ 2 }+2u\alpha +2v\beta +2w\gamma +d)=0\\ \Rightarrow \therefore \quad x\alpha +y\beta +z\gamma +u(x+\alpha )+v(y+\beta )+w(z+\gamma )+d=0…(4)

3.समतल का ध्रुव (Pole of Plane)-

समतल lx+my+nz=p का गोले { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }={ a }^{ 2 } के सापेक्ष ध्रुव ज्ञात करना।
(To find the pole of the plane lx+my+nz=p with repect to sphere { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }={ a }^{ 2 })
दिए हुए समतल का समीकरण
lx+my+nz=p ……..(1)
मान लो समतल (1) के ध्रुव (pole) के निर्देशांक (\alpha ,\beta ,\gamma ) हैं,तब (\alpha ,\beta ,\gamma ) का गोले { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }={ a }^{ 2 } के सापेक्ष ध्रुवीय समतल का समीकरण होगा

x\alpha +y\beta +z\gamma ={ a }^{ 2 }….(2)

यहां (1) व (2) एक ही समतल के समीकरण हैं अतः इनकी तुलना करने पर-

\frac { \alpha }{ l } =\frac { \beta }{ m } =\frac { \gamma }{ n } =\frac { { a }^{ 2 } }{ p } \\ \Rightarrow \alpha =\frac { { la }^{ 2 } }{ p } ,\beta =\frac { { ma }^{ 2 } }{ p } ,\gamma =\frac { { na }^{ 2 } }{ p }
अतः ध्रुव के अभीष्ट निर्देशांक हैं

(\frac { l{ a }^{ 2 } }{ p } ,\frac { { ma }^{ 2 } }{ p } ,\frac { { na }^{ 2 } }{ p } )

4.गोले के सापेक्ष ध्रुव एवं ध्रुवीय समतल (Pole and Polar plane respect to sphere) पर आधारित सवाल-

Question-1.रेखा \frac { x-1 }{ 2 } =\frac { y-2 }{ 3 } =\frac { z-3 }{ 4 } की गोले { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }=16के सापेक्ष ध्रुवीय रेखा का समीकरण ज्ञात करो।
(Find the polar line of the line \frac { x-1 }{ 2 } =\frac { y-2 }{ 3 } =\frac { z-3 }{ 4 } with respect to the sphere{ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }=16)
Solution-दी हुई रेखा व गोले के समीकरण हैं-

\frac { x-1 }{ 2 } =\frac { y-2 }{ 3 } =\frac { z-3 }{ 4 } =r
तथा { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }=16
रेखा (1) पर किसी बिन्दु के निर्देशांक हैं
(2r+1,3r+2,4r+3)
इस बिन्दु का गोले (2) के सापेक्ष ध्रुवीय समतल का समीकरण होगा-
x(2r+1)+y(3r+2)z(4r+3)=16
या r(2x+3y+4z)+(x+2y+3z-16)=0 ….(3)
r के सभी मानों के लिए समतल (3) निम्न सरल रेखा से गुजरता है-
2x+3y+4z=0, x+2y+3z-26=0 ……..(4)
यदि ध्रुवी रेखा के दिक्अनुपात l,m,n हो तो-
2l+3m+4n=0 ………(5)
l+2m+3n=0 ………(6)
(5) व (6) से-

\frac { l }{ 9-8 } =\frac { m }{ -2 } =\frac { n }{ -1 } \\ \frac { l }{ -1 } =\frac { m }{ -2 } =\frac { n }{ -1 }
(4) में z=0 रखने पर-
2x+3y=0 …….(7)
x+2y=16 ……..(8)
(8) को 2 से गुणा करने पर-
2x+4y=32 ………..(9)
2x+3y=0 …………(7)
– – घटाने पर-
————————–
y=32
y का मान समीकरण (8) में रखने पर-
x+64=16
x=-48
अतः बिन्दु (-48,32,0)से गुजरने वाली ध्रुवी रेखा का समीकरण-

\frac { x+48 }{ 1 } =\frac { y-32 }{ -2 } =\frac { z }{ 1 }

उपर्युक्त सवाल के हल द्वारा गोले के सापेक्ष ध्रुव एवं ध्रुवीय समतल (Pole and Polar plane respect to sphere) को समझा जा सकता है।

Question-2.रेखा \frac { x+1 }{ 2 } =\frac { y-1 }{ 3 } =\frac { z }{ 4 } की गोले { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }=9 के सापेक्ष ध्रुवीय रेखा का समीकरण ज्ञात करो।
(Find the polar line of \frac { x+1 }{ 2 } =\frac { y-1 }{ 3 } =\frac { z }{ 4 } with respect to the sphere { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }=9.)
Solution-दी हुई रेखा व गोले का समीकरण है-

\frac { x+1 }{ 2 } =\frac { y-1 }{ 3 } =\frac { z }{ 4 } =r….(1)
तथा { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }=9….(2)
रेखा (1) पर किसी बिन्दु के निर्देशांक हैं
(2r-1,3r+1,4r)
इस बिन्दु का गोले (2) के सापेक्ष ध्रुवीय समतल का समीकरण होगा-
x(2r-1)+y(3r+1)+z(4r)=9
या r(2x+3y+4z)+(-x+y-9)=0 ……..(3)
r के सभी मानों के लिए समतल (3) निम्न सरल रेखा से गुजरता है-
2x+3y+4z=0 , -x+y-9=0
2x+3y+4z=0 , x-y+9=0
जो कि अभीष्ट ध्रुवी रेखा का समीकरण है।

उपर्युक्त सवाल के हल द्वारा गोले के सापेक्ष ध्रुव एवं ध्रुवीय समतल (Pole and Polar plane respect to sphere) को समझा जा सकता है।
Question-3.प्रदर्शित कीजिए कि रेखा \frac { x+3 }{ 1 } =\frac { y+1 }{ 2 } =\frac { z-2 }{ 3 } की गोले { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }=1 के सापेक्ष ध्रुवीय रेखा \frac { x }{ -1 } =\frac { 7y+3 }{ 11 } =\frac { 2-7z }{ 5 } है।
(Show that lines \frac { x+3 }{ 1 } =\frac { y+1 }{ 2 } =\frac { z-2 }{ 3 } of with respect to the sphere { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }=1 is the line\frac { x }{ -1 } =\frac { 7y+3 }{ 11 } =\frac { 2-7z }{ 5 } .)
Solution-दी हुई रेखा व गोले का समीकरण है-

\frac { x+3 }{ 1 } =\frac { y+1 }{ 2 } =\frac { z-2 }{ 3 } =r….(1)
तथा { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }=1…(2)
रेखा (1) पर किसी बिन्दु के निर्देशांक है (r-3,2r-1,3r+2)
इस बिन्दु का गोले (2) के सापेक्ष ध्रुवीय समतल का समीकरण होगा-
x(r-3)+y(2r-1)+z(3r+2)=1
या r(x+2y+3z)+(-3x-y+2z-1)=0 ……(3)
r के सभी मानों के लिए समतल (3) निम्न सरल रेखाओं से गुजरता है-
x+2y+3z=0 …….(4)
-3x-y+2z-1=0 …..(5)
(4) व (5) में x=0 रखने पर-
2y+3z=0 ………(6)
-y+2z-1=0 ……….(7)
समीकरण (7) को 2 से गुणा करने पर-
2y+3z=0 …………(6)
-2y+4z-2=0 ………(8)
——————-जोड़ने पर
7z-2=0

z=\frac { 2 }{ 7 }

z का मान समीकरण (7) में रखने पर-

-y+2(\frac { 2 }{ 7 } )-1=0\\ \Rightarrow -y+\frac { 4 }{ 7 } -1=0\\ \Rightarrow y=\frac { -3 }{ 7 }
अतः बिन्दु=(0,\frac { -3 }{ 7 } ,\frac { 2 }{ 7 } )
माना ध्रुवी रेखा के दिक्अनुपात l,m,n हैं
l+2m+3n=0 ……….(9)
-3l-m+2n=0 ………..(10)
————————-
हल करने पर-

\frac { l }{ 4+3 } =\frac { m }{ -9-2 } =\frac { n }{ -1+6 } \\ \Rightarrow \frac { l }{ 7 } =\frac { m }{ -11 } =\frac { n }{ 5 }
अतः ध्रुवी रेखा का समीकरण होगा-

\frac { x-0 }{ 7 } =\frac { y+\frac { 3 }{ 2 } }{ -11 } =\frac { z-\frac { 2 }{ 7 } }{ 5 } \\ \Rightarrow \frac { x }{ 7 } =\frac { 7y+3 }{ -77 } =\frac { 7z-2 }{ 35 } \\ \Rightarrow \frac { x }{ -1 } =\frac { 7y+3 }{ 11 } =\frac { 2-7z }{ 5 }

उपर्युक्त सवाल के हल द्वारा गोले के सापेक्ष ध्रुव एवं ध्रुवीय समतल (Pole and Polar plane respect to sphere) को समझा जा सकता है।
Question-4.सिद्ध कीजिए कि \frac { x }{ 2 } =\frac { y-1 }{ 3 } =\frac { z+3 }{ 4 } के किसी बिन्दु पर तथा गोले { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }=1के सापेक्ष एक ध्रुवीय समतल,रेखा \frac { 2x+3 }{ 13 } =\frac { y-1 }{ -3 } =\frac { -z }{ 1 } से गुजरता है।
(Prove that the polar plane of any point on the line \frac { x }{ 2 } =\frac { y-1 }{ 3 } =\frac { z+3 }{ 4 } with respect to the sphere { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }=1 passes through the line\frac { 2x+3 }{ 13 } =\frac { y-1 }{ -3 } =\frac { -z }{ 1 } .)
Solution-दी हुई रेखा व गोले का समीकरण-

\frac { x }{ 2 } =\frac { y-1 }{ 3 } =\frac { z+3 }{ 4 } =r
तथा { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }=1
रेखा (1) पर किसी बिन्दु के निर्देशांक (2r,3r+1,4r-3)
इस बिन्दु का गोले (2) के सापेक्ष ध्रुवीय समतल का समीकरण होगा-
x(2r)+y(3r+1)+z(4r-3)=1
या r(2x+3y+4z)+y-3z-1=0
r के सभी मानों के लिए समतल (3) निम्न सरल रेखाओं से गुजरता है-
2x+3y+4z=0 ……(3)
y-3z-1=0 …….(4)
जब z=0 तो (4) से y=1
z व y का मान (3) में रखने पर-

2x+3=0\Rightarrow x=\frac { -3 }{ 2 }
अतः बिन्दु=(\frac { -3 }{ 2 } ,1,0)
यदि ध्रुवी रेखा के दिक्अनुपात l,m,n हैं तो-
2l+3m+4n=0 ……..(5)
0.l++m-3n=0 ………(6)
हल करने पर-

\frac { l }{ -9-4 } =\frac { m }{ 0+6 } =\frac { n }{ 2-0 } \\ \Rightarrow \frac { l }{ -13 } =\frac { m }{ 6 } =\frac { n }{ 2 }
अतः ध्रुवी रेखा का समीकरण होगा-

\frac { x+\frac { -3 }{ 2 } }{ -13 } =\frac { y-1 }{ 6 } =\frac { z-0 }{ 2 } \\ \frac { 2x+3 }{ -13 } =\frac { y-1 }{ 3 } =\frac { z }{ 1 }
उपर्युक्त सवालों के हल द्वारा गोले के सापेक्ष ध्रुव एवं ध्रुवीय समतल (Pole and Polar plane respect to sphere) को समझा जा सकता है।

5.वृत्त में ध्रुव और ध्रुवीय क्या है? (What is pole and polar in circle?, pole and polar of a circle)-

ज्यामिति में, ध्रुव और ध्रुव क्रमशः एक बिंदु और एक रेखा होते हैं जिनका एक विशिष्ट शंकुधारी खंड के संबंध में एक अद्वितीय पारस्परिक संबंध होता है।किसी दिए गए सर्कल के लिए, एक सर्कल में पारस्परिकता का मतलब है कि समतल के प्रत्येक बिंदु को उसकी ध्रुवीय रेखा में और समतल के प्रत्येक रेखा को उसके ध्रुव में बदलना।

6.सीधी रेखा का ध्रुव क्या है? (What is pole of straight line?)-

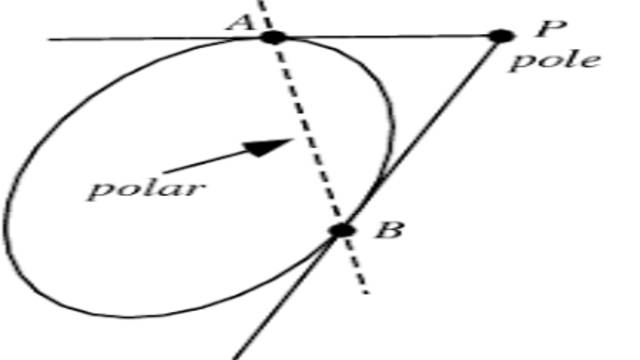
P से गुजरने वाले किसी भी चाप AB और A’B’ को ड्रा करें। यदि A और B के वृत्त पर स्पर्श रेखाएँ Q से मिलती हैं, तो Q के स्थान को वृत्त के संबंध में P का ध्रुवीय कहा जाता है और P को ध्रुव कहा जाता है और यदि स्पर्शरेखा को A’ और B’ पर मिलने वाला वृत्त Q’ पर मिलता है, फिर सीधी रेखा QQ’ ,P के साथ ध्रुव है।

7.क्या जेईई पाठ्यक्रम में पोल ​​और ध्रुवीय है? (Is pole and polar in JEE syllabus?)-

हालांकि, इस तरह के प्रश्न के अन्य तरीके हैं, ध्रुव और ध्रुवीय का ज्ञान प्रश्न को तेजी से हल करने में मदद करता है और यदि अन्य विधि ली जाती है तो कठोर गणना से बचें।
नहीं, यह जेईई पाठ्यक्रम में नहीं है और अब तक इस विषय से कोई प्रश्न नहीं पूछा गया है।

8.आप ध्रुवीय निर्देशांक में एक रेखा का प्रतिनिधित्व कैसे करते हैं? (How do you represent a line in polar coordinates?)-

इस प्रकार, मूलबिन्दु के माध्यम से एक रेखा के समीकरण को समीकरण q = a द्वारा ध्रुवीय निर्देशांक में दर्शाया जाता है। एक रेखा का ध्रुवीय समीकरण।

9.एक सर्कल सूत्र के संबंध में एक सीधी रेखा का ध्रुव (pole of a straight line with respect to a circle formula)-

P को वृत्त के अंदर या बाहर कोई बिंदु मान लें।यदि A और B के वृत्त की स्पर्श रेखाएँ Q से मिलती हैं, तो Q के बिन्दुपथ को वृत्त के संबंध में P का ध्रुव कहा जाता है और P को ध्रुव कहा जाता है और यदि A’ और B’ वृत्त को स्पर्शरेखा Q’ पर मिलते हैं , तो सीधी रेखा QQ’ ,P के साथ ध्रुव है।

10.परवलय के ध्रुव और ध्रुवीय (pole and polar of parabola)-

यदि A और B पर पैराबोला से स्पर्श रेखाएँ Q (h, k) पर मिलती हैं, तो Q के बिन्दुपथ को Parabola के संबंध में P का ध्रुवीय कहा जाता है और P को ध्रुव कहा जाता है और यदि parabola के A’ और B’ पर स्पर्शरेखा Q’ पर मिलती है,फिर सीधी रेखा QQ’ ,P के ध्रुव के रूप में ध्रुवीय है। किसी भी स्पर्शरेखा को उसके स्थिर बिंदु का ध्रुवीय कहा जाता है।

11.पोल और ध्रुवीय समतल को परिभाषित करें (define pole and polar plane)-

ज्यामिति में, ध्रुव और ध्रुव क्रमशः एक बिंदु और एक रेखा होते हैं जिनका एक विशिष्ट शंकुधारी खंड के संबंध में एक अद्वितीय पारस्परिक संबंध होता है।किसी दिए गए सर्कल के लिए, एक सर्कल में पारस्परिकता का मतलब है कि समतल के प्रत्येक बिंदु को उसकी ध्रुवीय रेखा में और समतल की प्रत्येक रेखा को उसके ध्रुव में बदलना।

12.कॉनिकॉइड का ध्रुवीय समतल (polar plane of conicoid)-

स्पर्शरेखा: एक रेखा जो दो संयोग बिंदुओं में एक कोनिकॉइड से मिलती है उसे कॉनिकॉइड की स्पर्शरेखा रेखा कहा जाता है।
ध्रुवीय समतल:एक चतुर्भुज के संबंध में बाहरी बिंदु P का ध्रुवीय समतल वह समतल है जिसमें P से चतुष्कोण तक खींची गई सभी स्पर्श रेखाओं के संपर्क के बिंदु होते हैं।

13.एक वृत्त के संबंध में एक बिंदु के ध्रुवीय का समीकरण, एक सर्कल सूत्र के संबंध में एक बिंदु का ध्रुवीय (equation of polar of a point with respect to a circle, polar of a point with respect to a circle formula)-

P को वृत्त के अंदर या बाहर कोई भी बिंदु मान लें।यदि वृत्त के A और B बिन्दु पर स्पर्श रेखाएँ Q से मिलती हैं, तो Q के बिन्दुपथ को वृत्त के संबंध में P का ध्रुवीय कहा जाता है और P को ध्रुव कहा जाता है और यदि वृत्त के A’ और B’ पर स्पर्शरेखा Q’ पर मिलती हैं तो सीधी रेखा QQ’ ,P के साथ ध्रुव है।

14.एक गोले की ध्रुवीय रेखाएँ (polar lines of a sphere)-

एक वृत्त C में एक रेखा L का ध्रुव एक बिंदु P है जो L पर बिंदु Q के C में व्युत्क्रम है जो वृत्त के केंद्र के सबसे निकट है। इसके विपरीत, एक वृत्त C में बिंदु P की ध्रुवीय रेखा (या ध्रुवीय) रेखा L है, जो वृत्त के केंद्र में इसका निकटतम बिंदु Q, P के C में व्युत्क्रम है।

Also Read This Article:-Orthogonality condition of two spheres

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Twitter	click here
4.	Instagram	click here
5.	Linkedin	click here
6.	Facebook Page	click here