Number Theory History and Overview
1.संख्या सिद्धांत :इतिहास और अवलोकन का परिचय (Introduction to Number Theory History and Overview), संख्या सिद्धांत -इतिहास और अवलोकन (Number Theory–History and Overview):
- संख्या सिद्धांत:इतिहास और अवलोकन (Number Theory History and Overview) के इस आर्टिकल में बताया गया है कि मनुष्य के उद्भव के पश्चात जब से गणित का प्रारम्भ हुआ है तो गणित तथा उसकी संख्याओं ने हमें गहराई से प्रभावित किया है। गणित को ब्रह्माण्ड की जीभ कहा गया है जिसका तात्पर्य है कि जैसे जीभ के बिना मनुष्य बोल नहीं सकता अपने भावों को व्यक्त नहीं कर सकता है। ठीक इसी प्रकार गणित के बिना हम न तो लेनदेन का हिसाब लगा सकते है ,न आपस का व्यावसायिक व्यवहार का पालन कर सकते है। गणित की शाखा है संख्या पद्धति। संख्या पद्धति को गणित की रानी कहा गया है . अर्थात संख्याओं के बिना गणित की संरचनाओं ,प्रमेयों ,सिद्धान्तों को ठीक प्रकार से व्यक्त नहीं किया जा सकता है।
- वर्तमान समय में संख्या पद्धति का इतना महत्त्व बढ़ गया है कि इसे गणित का राजा कहा जा सकता है ,जैसे राज्य का शासन राजा के बिना नहीं चलाया जा सकता है ,उसी प्रकार संख्या पद्धति के बिना गणित का के बिना गणित का कार्य सुचारु रूप से नहीं चलाया जा सकता है। संख्या पद्धति के आधार पर ही ज्यामिति का कार्य ठीक प्रकार से किया जा सकता है।
- इस आर्टिकल में संख्या पद्धति के बारे में बताया गया है तथा उसका कितना महत्त्व है यह प्रदर्शित किया गया है।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:geometric proof of difference of squares
2.भाग I-नंबर थ्योरी क्या है और आज यह प्रासंगिक क्यों है? (Part I-What is Number Theory and Why is it Relevant Today?), संख्या सिद्धांत :इतिहास और अवलोकन (Number Theory History and Overview):
- गणित ब्रह्मांड की प्राकृतिक जीभ है।एक प्रजाति के रूप में हमारे अस्तित्व की शुरुआत के बाद से, संख्याओं ने हमें गहराई से मोहित किया है। अक्सर हमारे महान विचारकों को ब्रह्मांड के कई गहरे रहस्यों को उजागर करने के लिए आमंत्रित करना, प्राकृतिक संख्याओं का अध्ययन, संख्या सिद्धांत, गणित की सबसे पुरानी शाखाओं में से एक है।
- नंबर थ्योरी की शुद्धता ने पीढ़ी-दर-पीढ़ी गणितज्ञों को कैद कर लिया है-प्रत्येक उस शाखा में योगदान देता है जिसे कार्ल गौस ने “गणित की रानी” के रूप में वर्णित किया है। अपेक्षाकृत हाल की सफलताओं तक, नंबर थ्योरी ने शुद्ध गणित के राजा के रूप में शासन किया। आज, हालांकि, नंबर थ्योरी की एक बुनियादी समझ अत्याधुनिक सॉफ्टवेयर इंजीनियरिंग,विशेष रूप से सुरक्षा-आधारित सॉफ़्टवेयर के लिए एक महत्वपूर्ण आलोचनात्मक अग्रदूत है। नंबर थ्योरी क्रिप्टोग्राफी के केंद्र में है-जो खुद में तेजी से विकास की एक आकर्षक अवधि का अनुभव कर रहा है, प्रसिद्ध आरएसए एल्गोरिदम से लेकर जंगली-लोकप्रिय ब्लॉकचेन दुनिया तक।
- इतिहास में दो अलग-अलग क्षण संख्या सिद्धांत के विकास में विभक्ति बिंदु के रूप में सामने आते हैं।सबसे पहले,पुरातन समय में,यूक्लिड ने अपने जीसीडी (ग्रेटेस्ट कॉमन डिविज़र) एल्गोरिदम को आगे बढ़ाया-शानदार चरणों का एक सेट जो ज्यामितीय टिप्पणियों का उपयोग करके उनके सरलतम रूप में अंशों को सरल बनाता है।फिर, लगभग दो-हज़ार साल बाद, कार्ल गॉस ने यूक्लिड के अनौपचारिक लेखन को अपने स्वयं के व्यापक सबूतों के साथ टाइमलेस डिसक्विस्टेंस अरिथमेटिका में एक साथ शादी करके औपचारिक रूप दिया।
Also Read This Article:Number Theory
3.यूक्लिड एंड द ग्रेटेस्ट कॉमन डिविज़र (Euclid and the Greatest Common Divisor):
- एक शाखा के रूप में नंबर थ्योरी की उत्पत्ति सभी विशेष रूप से एक यूक्लिड के जीवनकाल के लिए,बीसीएस के लिए वापस जाती है।एक असाधारण गणितज्ञ,अलेक्जेंड्रिया के यूक्लिड,जिसे “फादर ऑफ ज्योमेट्री” के रूप में भी जाना जाता है,ने रिकॉर्ड किए गए सबसे पुराने “एल्गोरिदम” (यहां पर चरण-दर-चरण संचालन का एक सेट है) को सामने रखा।यह एल्गोरिथ्म,ग्रेटेस्ट कॉमन डिविज़र (Greatest Common Divisor),नंबर थ्योरी के लिए हमारे किक ऑफ बिंदु के रूप में समय की कसौटी पर खड़ा है क्योंकि यह प्राकृतिक संख्याओं में आकर्षक गुणों के कारण है।
300 ई.पू. के आसपास,यूक्लिड ने अपनी क्लासिक एलिमेंट्स बुक सीरीज़ को हासिल किया;पूर्णांक से लेकर सेगमेंट और सतह क्षेत्रों तक विषयों की एक श्रृंखला के साथ दस पुस्तकों की एक श्रृंखला।दिलचस्प बात यह है कि उनका जीसीडी (Greatest Common Divisor) एल्गोरिदम एक बार नहीं बल्कि दो बार इस श्रृंखला में सूचीबद्ध किया गया है -पहले बुक 7 में (संख्याओं के साथ प्रस्तुत किया गया),फिर बाद में बुक 10 (ज्यामिति के माध्यम से प्रस्तुत किया गया) में। - गणित के इतिहासकारों के अनुसार, यह संभावना है कि एल्गोरिथ्म का उत्तरार्द्ध रूप,एक ज्यामिति (पुस्तक 10) में ग्राउंडेड है,वास्तव में विकल्प से पहले,संख्या 7 में पाया गया संख्या-आधारित रूप।लंबाई,क्षेत्रों और संस्करणों के साथ काम करना, यह है यह माना जाता है कि जीसीडी एल्गोरिथ्म यूक्लिड के लिए बहुत महत्व का था क्योंकि यह किसी भी दो खंडों (A) और (B) के बीच सबसे बड़ी आम लंबाई को खोजने का एक तरीका प्रदान करता था।वह जिस अवधि में रहते थे,उसे देखते हुए,यह अत्यधिक संभावना है कि यह अवलोकन किसी के लिए भी बहुत उपयोगी था और किसी भी प्रकार के निर्माण (चिनाई,बढ़ईगीरी, आदि …) में शामिल था।
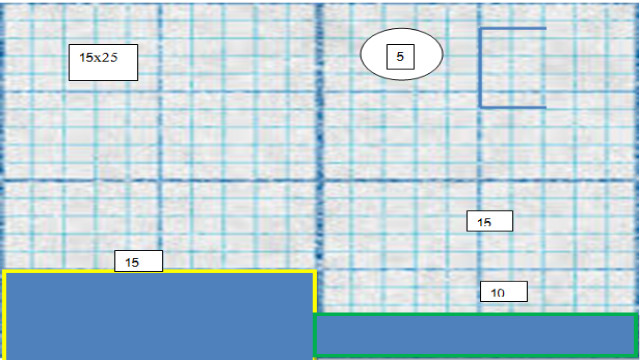
- पिछली परिभाषा पर विस्तार करते हुए,ग्रेटेस्ट कॉमन डिविज़र,ज्यामितीय रूप से बोलने वाला,दो लंबाई (A) और (B) की सबसे बड़ी लंबाई (छ) है जो समान रूप से A और B मापता है; वैकल्पिक रूप से,लंबाई (A) और (B) दोनों लंबाई (G) के पूर्णांक गुणक हैं।एक ज्यामितीय उदाहरण नीचे दिया गया है – कल्पना करें कि हमने 15 मीटर x 25 मीटर के फर्श के साथ काम किया है।लागत को कम करने के लिए,हम केवल एक ही आकार की टाइल लंबाई खरीदना चाहते हैं;जिसकी आवश्यकता है कि हम टाइल की सबसे बड़ी लंबाई (मीटर में) की गणना करें,जो पूरी तरह से फिट हो,लंबाई और चौड़ाई दोनों में,बिना अलग किए।दूसरे शब्दों में 15 और 25 के महत्तम समापवर्तक क्या है?
- हमने अपने उदाहरण के लिए जीसीडी की गणना में शामिल विशिष्ट चरणों पर काम किया है,लेकिन उम्मीद है ऊपर दिए गए चित्रण में शामिल ज्यामिति की सहज समझ है।जैसा कि बताया गया है,हमारे उदाहरण के प्रश्न का उत्तर 5 मीटर है,जो वास्तव में 15 और 25 में पाया जाने वाला सबसे बड़ा उभयणिष्ठ पूर्णांक है।
4.गॉस एंड द फंडामेंटल प्रमेय ऑफ अरिथमेटिक (Goss and the fundamental theorem of arithmetic):
- नंबर थ्योरी में निम्नलिखित बड़ी छलांग यूक्लिड के बाद लगभग~2000 वर्षों से एक ब्रेक के माध्यम से उपजी है।21 साल की तेजस्वी युवावस्था में, एक कार्ल गॉस ने एक शोध प्रबंध किया,जिसमें यूक्लिड के तत्त्वों के साथ आधुनिक गणित से विवाह किया था।उनके कृति प्रकाशन, डिस्क्विस्टनेस अरिथमेटिकेट (“अंकगणित जांच में अनूदित) कई शानदार और सटीक तरीकों को पैक किया,जबकि जरूरी नहीं कि उनके सभी मूल काम,संख्या सिद्धांत के क्षेत्र को व्यवस्थित और व्यवस्थित किया।इस प्रकाशन के साथ उन्होंने पहले से बिखरी और अनौपचारिक विधियों को औपचारिक रूप देकर,महत्वपूर्ण बकाया समस्याओं के मूल उत्तर प्रदान करते हुए और भविष्य के योगदानकर्ताओं के लिए परिदृश्य का पता लगाकर शाखा की स्थापना की।
- शोध की आधारशिला यूरेका पल एक अब कालातीत प्रमेय है जिसे मौलिक सिद्धांत के मौलिक के रूप में जाना जाता है:
- 1 से अधिक कोई भी पूर्णांक या तो एक अभाज्य है या उसे अभाज्य संख्याओं (आदेश की अनदेखी) के अनूठे गुणन के रूप में लिखा जा सकता है।
- उपर्युक्त परिभाषा दो अलग-अलग भागों में विभाजित होकर पचने योग्य हो जाती है।पहला,कहता है कि 1 से अधिक पूर्णांक या तो स्वयं अभाज्य है या कड़ाई से अभाज्य संख्याओं को गुणा करके निर्मित किया जा सकता है।दूसरा भाग यह गारंटी देता है कि प्रत्येक गैर-अभाज्य (मिश्रित) संख्या के लिए,इन अभाज्य संख्याओं को गुणा करने का केवल एक ही तरीका है,(फिर से,आदेश की अनदेखी)।
- एक और तरीका है,अभाज्य हैं (गुणक) पूर्णांक के “बिल्डिंग ब्लॉक”:अभाज्य के गुणक (पूर्णतः) सभी पूर्णांक उत्पन्न करेंगे।यह परिणाम निस्संदेह पिछली शताब्दियों के गणितज्ञों के लिए जाना जाता था,लेकिन गॉस,इन डिसक्वीज़न,इसे औपचारिक रूप से बताने और कठोर प्रमाण देने वाले पहले व्यक्ति थे।
5.ऑन-क्राफ्ट चालाक क्रिप्टोग्राफ़िक अनुप्रयोग (On-craft clever cryptographic applications):
- अब संख्या सिद्धांत के मूल इतिहास और इसके प्रभाव की गहराई में एक त्वरित पूर्वावलोकन से लैस है,यह संख्या सिद्धांत के भीतर सबसे अधिक लागू विषय के साथ खुद को परिचित करने का समय है: क्रिप्टोग्राफी।
जैसा कि हम अगला देखेंगे,जबकि गॉस ने औपचारिक रूप से शाखा के लिए मंच निर्धारित किया है,क्रिप्टोग्राफ़िक सिस्टम के शुरुआती उदाहरण पहले से ही अस्तित्व में थे,जिसमें बहुत साहसी दांव थे।उन कुछ उदाहरणों के माध्यम से,हम बुनियादी,सामान्य क्रिप्टोग्राफी सिद्धांतों को एक्सट्रपलेट करेंगे;जो बाद में,हमें आधुनिक समय में सबसे महत्वपूर्ण सुरक्षा एल्गोरिदम में से एक को तोड़ने-समझने और समझने में मदद करेगा:आरएसए एल्गोरिथ्म। - उपर्युक्त आर्टिकल में संख्या सिद्धांत–इतिहास और अवलोकन (Number Theory History and Overview) के बारे में बताया गया है.
Number Theory History and Overview
संख्या सिद्धांत:इतिहास और अवलोकन
(Number Theory History and Overview)
Number Theory History and Overview
संख्या सिद्धांत:इतिहास और अवलोकन (Number Theory History and Overview) के इस आर्टिकल में बताया गया है कि
मनुष्य के उद्भव के पश्चात जब से गणित का प्रारम्भ हुआ है तो गणित तथा उसकी संख्याओं ने हमें गहराई से प्रभावित किया है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
