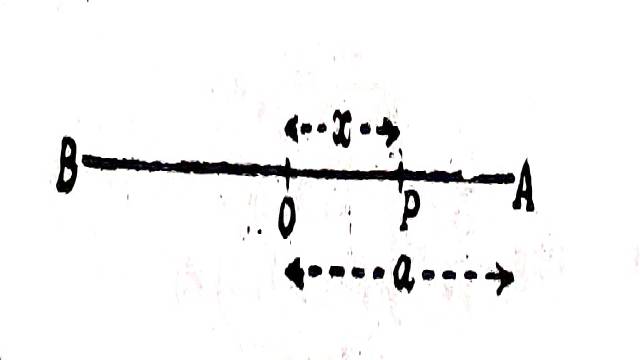Motion in Resisting Medium
1.प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium),वेग के समानुपाती प्रतिरोध के अधीन उर्ध्वाधर गति (Vertical Motion Under Resistance Proportional to Velocity):
प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium) के इस आर्टिकल में वेग के समानुपाती प्रतिरोध के अधीन उर्ध्वाधर गति पर आधारित सवालों को हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Theorem of Parallel Axes in Dynamics
2.प्रतिरोधी माध्यम में सरल रेखीय गति के साधित उदाहरण (Rectilinear Motion in Resisting Medium Solved Examples):
Example:1.एक सरल रेखा में कण प्रतिरोध k v^3 में गतिमान है,जहाँ v वेग है।दर्शाइए कि यदि दूरी s होने पर समय t पर वेग v है, V=\frac{u}{(1+k s u)} ; t=\left(\frac{s}{u}\right)+\frac{1}{2} k s^2
जहाँ u प्रारम्भिक वेग है।
(A particle moving in a straight line is subjected to a resistance k v^3,where v is the velocity.show that if v is velocity at time t when the distance is s, V=\frac{u}{(1+k s u)} ; t=\left(\frac{s}{u}\right)+\frac{1}{2} k s^2
Where u is the initial velocity)
Solution:कण गुरुत्वाकर्षण के अधीन न तो गिर रहा है और न ऊपर गति कर रहा है,अतः भार mg कार्य नहीं कर रहा है। अतः कण पर प्रतिरोध -m k v^3 कार्य कर रहा है।
गति का समीकरण
m v \frac{d v}{d s}=-m k v^3 \\ \Rightarrow-\frac{d v}{v^2}=k d s
समाकलन करने पर:
\frac{1}{v}=k s+C
जहाँ C समाकलन नियतांक है।
प्रारम्भ में जब s=0,v=u \therefore C =\frac{1}{u} \\ \therefore \frac{1}{v}=k s+\frac{1}{u} \\ \Rightarrow \frac{1}{v}=\frac{u k s+1}{u} \\ \Rightarrow v=\frac{u}{u k s+1} \cdots(1) \\ \Rightarrow \frac{d s}{d t} =\frac{u}{u k s+1} \left[\because \frac{d s}{d t}=v\right] \\ \int(u k s+1) ds=u d t \\ \Rightarrow \frac{1}{2} u k s^2+s+C^{\prime}=u t
जहाँ C’ समाकलन नियतांक है।
प्रारम्भ में जब t=0,s=0, \therefore C^{\prime}=0 \\ \frac{1}{2} u k s^2+s=u t \\ \Rightarrow t=\frac{s}{u}+\frac{1}{2} k s^2 \cdots(2)
Example:2.एक कण को वेग V से एक चिकने क्षैतिज तल में प्रक्षिप्त किया जाता है जिसका प्रति इकाई द्रव्यमान प्रतिरोध वेग के घन का \mu गुना है।दर्शाइए कि समय t में यह दूरी तय करता है वह है
\frac{1}{\mu V} \quad\left[\sqrt{\left(1+2 \mu t V^2\right)-1}\right]
तथा इसका तब वेग \frac{V}{\sqrt{\left(1-2 \mu t V^2\right)}} है।
(A particle is projected with velocity V along a smooth horizontal plane in a medium whose resistance per unit mass is \mu times the cube of the velocity. Show that the distance it has described in time t is
\frac{1}{\mu V} \quad\left[\sqrt{\left(1+2 \mu t V^2\right)-1}\right]
and that is velocity then is \frac{V}{\sqrt{\left(1-2 \mu t V^2\right)}})
Solution:कण क्षैतिज तल में गति कर रहा है,अतः भार mg कार्य नहीं कर रहा है।केवल कण पर बल कार्य कर रहा है तथा यह -m \mu v^3 है।
कण की गति का समीकरण
m\left(\frac{d v}{d t}\right)=-m \mu v^3 \\ \Rightarrow-\frac{d v}{v^3}=\mu d t
समाकलन करने पर:
\frac{1}{2 v^2}=\mu t+C
जहाँ C समाकलन नियतांक है।
प्रारम्भ में जब t=0,v=V, \therefore C=\frac{1}{2V^2} \\ \therefore \frac{1}{2 v^2}=\mu t+\frac{1}{2 V^2} \\ \Rightarrow \frac{1}{v^2}=\frac{2 \mu t V^2+1}{V^2} \\ \Rightarrow v=\frac{V}{\sqrt{\left(1+2 \mu t V^2\right)}} \cdots(1)
यदि कण द्वारा t समय में x दूरी तय की जाती है तो समीकरण (1) से:
\frac{d x}{d t}=\frac{V}{\sqrt{\left(1+2 \mu t V^2\right)}} \\ \Rightarrow \int d x=\int \frac{V}{\sqrt{\left(1+2 \mu t V^2\right)}} d t \\ \Rightarrow x=\frac{V\left(1+2 \mu t V^2\right)^{\frac{1}{2}}}{2 \mu V^2 \times \frac{1}{2}}+C^{\prime} \\ \Rightarrow x=\frac{1}{\mu V} \sqrt{\left(1+2 \mu t V^2\right)}+C^{\prime} \cdots(2)
प्रारम्भ में जब t=0,x=0 ,\therefore C^{\prime}=-\frac{1}{\mu V}
समीकरण (2) में मान रखने पर:
x =\frac{1}{\mu V} \sqrt{\left(1+2 \mu t V^2\right)}-\frac{1}{\mu V} \\ \Rightarrow x=\frac{1}{\mu V}\left[\sqrt{\left(1+2 \mu t V^2\right)}-1\right]
Example:3.m द्रव्यमान का एक कण गुरुत्वाकर्षण के अधीन एक ऐसे माध्यम से गिर रहा है जिसका प्रतिरोध वेग का \mu गुना है। यदि कण को विरामावस्था से छोड़ा गया था,तो दर्शाइए कि समय t में तय की गई दूरी है:
\frac{g m^2}{\mu^2}\left[e^{-\left(\frac{\mu}{m}\right) t}+\frac{\mu t}{m}-1\right]
(A particle of mass m is falling under the influence of gravity through a medium whose resistance equal \mu times the velocity. If the particle were released from rest, show that the distance fallen through in time t is)
\frac{g m^2}{\mu^2}\left[e^{-\left(\frac{\mu}{m}\right) t}+\frac{\mu t}{m}-1\right]
Solution:कण गुरुत्वाकर्षण के अधीन नीचे की ओर गिर रहा है।माना किसी क्षण कण का वेग v है,तब उस क्षण गति का प्रतिरोध है जो उर्ध्वाधर ऊपर की ओर कार्य कर रहा है।कण का भार उर्ध्वाधर नीचे की ओर कार्य कर रहा है।नीचे की दिशा में गति का समीकरण है:
m \frac{d v}{d t}=m g-k v \\ \Rightarrow \frac{d v}{d t}+\frac{\mu}{m} v=g \cdots(1)
यह v में रैखिक अवकल समीकरण है अतः
समाकलन गुणक (I. F.)=e^{\int\left(\frac{\mu}{m}\right) d t}=e^{a\left(\frac{\mu}{m}\right) t}
समीकरण (1) के दोनों पक्षों को I. F. से गुणा करके समाकलन करने पर:
v e^{\left(\frac{\mu}{m}\right) t}=\int g e^{\left(\frac{\mu}{m}\right) t} d t+A \\ \Rightarrow v e^{\left(\frac{\mu}{m}\right) t}=\frac{g e^{\left(\frac{\mu}{m}\right) t}}{\left(\frac{\mu}{m}\right)}+A \\ \Rightarrow v e^{\left(\frac{\mu}{m}\right) t}=\frac{m g}{\mu} e^{\left(\frac{\mu}{m}\right) t}+A \cdots(2)
प्रारम्भ में v=0 जब t=0 \therefore A=-\frac{m g}{\mu}
समीकरण (2) से:
v e^{\left(\frac{\mu}{m}\right) t}=\frac{m g}{\mu} e^{\left(\frac{\mu}{m}\right) t}-\frac{m g}{\mu} \\ \Rightarrow v=\frac{m g}{\mu}\left(1-e^{-\left(\frac{\mu}{m}\right) t}\right) \\ \Rightarrow \frac{d x}{d t}=\frac{m g}{\mu}\left(1-e^{-\left(\frac{\mu}{m}\right) t}\right)\left[\because v=\frac{d x}{d t}\right] \\ \Rightarrow \int d x=\int \frac{m g}{\mu}\left(1-e^{-\left(\frac{\mu}{m}\right) t}\right) d t \\ \Rightarrow x=\frac{m g}{\mu} \left[t+\frac{m}{\mu} e^{-\left(\frac{\mu}{m}\right) t}\right]+B \cdots(3)
जहाँ B समाकलन नियतांक है।
प्रारम्भ में जब t=0 तो x=0, \therefore B=-\frac{m^2 g}{\mu^2}
समीकरण (3) से:
x=\frac{m g}{\mu}\left[t+\frac{m}{\mu} e^{-\left(\frac{\mu}{m}\right) t}\right]-\frac{g m^2}{\mu^2} \\ \Rightarrow x=\frac{g m^2}{\mu^2}\left[\frac{\mu t}{m}+e^{-\left(\frac{\mu}{m}\right) t}-1\right]
Example:4.एक m द्रव्यमान के कण को उर्ध्वाधर प्रक्षिप्त किया जाता है ;हवा का प्रतिरोध वेग का mk गुना है।सिद्ध करो कि कण द्वारा अधिकतम ऊँचाई तय की जाती है वह है:
\left(\frac{v^2}{g}\right)[\lambda-\log (1+\lambda)]
जहाँ V कण का अन्तिम वेग तथा प्रारम्भिक वेग है।
(A particle of mass m is projected vertically under gravity ;the resistance of the air being mk times the velocity.Show that the greatest height attained by the particle is
\left(\frac{v^2}{g}\right)[\lambda-\log (1+\lambda)]
Where V is the terminal velocity of the particle and is the initial velocity)
Solution:कण को गुरुत्वाकर्षण के अधीन ऊपर फेंका जाता है।अतः गति का समीकरण
m v \frac{d v}{d x} =-m g-m k v \\ \Rightarrow v \frac{d v}{d x} =-g\left(1+\frac{k}{g} v\right) \cdots(1)
अन्तिम वेग V ज्ञात करने हेतु,नीचे की ओर गति का समीकरण है:
m v\left(\frac{d v}{d x}\right)=m g-m kv \cdots(2)
जब नीचे की ओर त्वरण शून्य है तब कण का वेग अन्तिम वेग होगा।अतः समीकरण (2) से अन्तिम वेग V है:
mg-m k V=0 \Rightarrow V=\frac{g}{k} \cdots(3)
समीकरण (1) में (3) से मान रखने पर:
v \frac{d v}{d x} =-g\left(1+\frac{v}{V}\right) \\ =-\frac{g}{V}(V+v) \\ \Rightarrow \frac{v d v}{V+v} =-\frac{g}{V} dx \\ \Rightarrow \frac{(v+V)-V}{v+V} d v=-\frac{g}{V} d x \\ \left(1-\frac{V}{v+V}\right) d v=\int \frac{g}{V} d x \\ v-V \log (V+v)=\frac{-g x}{V}+A \cdots(4)
प्रारम्भ में जब x=0 , v=\lambda V(दिया है)
\therefore A=\lambda V-V \log (V+\lambda V)
A का मान समीकरण (4) में रखने पर:
v-V \log (V+v)=-\frac{g x}{V}+\lambda V-V \log (v+\lambda V) \\ \Rightarrow \frac{g x}{V}=\lambda V-V \log [V(1+\lambda)]-v+V \log (V+v) \\ =\lambda V-v \log V-V \log (1+\lambda)-v+V \log (V+v) \cdots(5)
यदि कण द्वारा अधिकतम h ऊँचाई तय की जाती है तब x=h, v=0
समीकरण (5) से:
\frac{g h}{V}=\lambda V-v \log V-V \log (1+\lambda)-0+V \log V \\ \Rightarrow \frac{g h}{V}=\lambda V-V \log (1+\lambda) \\ \Rightarrow h =\left(\frac{V^2}{g}\right)[\lambda-\log (1+\lambda)]
Example:5.एक कण को वेग V से उर्ध्वाधर ऊपर की ओर फेंका जाता है और हवा का प्रतिरोध मंदन K v^2 उत्पन्न करता है,जहां v वेग है।सिद्ध करो कि वह वेग V’ से प्रक्षेप बिंदु पर लौटता है जो निम्न है:
\frac{1}{\left(V^{\prime}\right)^2}=\frac{1}{V^2}+\frac{k}{g}
(A particle is projected vertically upwards with velocity V and the resistance of the air produces a retardation K v^2, where v is the velocity.Show that the velocity V’ with which the particle return to the point of projection is given by)
\frac{1}{\left(V^{\prime}\right)^2}=\frac{1}{V^2}+\frac{k}{g}
Solution:जब कण को ऊपर की ओर फेंका जाता है तो कण की गति का समीकरण:
m v \frac{d v}{d x}=-m g-m k v^2 \cdots(1)
कण अधिकतम ऊँचाई B पर पहुँचता है और पुनः नीचे की ओर लौटता है।नीचे की ओर लौटने पर कण की गति का समीकरण
m v\left(\frac{d v}{d y}\right)=m g-m k v^2 \cdots(2)
यदि V_1 अन्तिम वेग हो तो, v \frac{d v}{d y}=0 तथा v=V_1 रखने पर:
0=m g-m k V_1^2 \Rightarrow V_1^2=\frac{g}{k} \cdots(3)
समीकरण (1) से:
v \frac{d v}{d x}=-g\left(1+\frac{K}{g} v^2\right) \\ =\int \frac{2 v}{1+\frac{K}{g} v^2} d v=-2 \int g d x \\ \frac{g}{K} \log \left(1+\frac{K}{g} v^2\right)=-2 g x+A_1 \cdots(4)
प्रारम्भ में जब x=0,v=V (दिया है)
\therefore A_1=\frac{g}{K} \log \left(1+\frac{K}{g} V^2\right) \\ A_1 का मान समीकरण (4) में रखने पर:
\frac{g}{K} \log \left(1+\frac{K}{g} v^2\right)=-2g x+\frac{g}{K} \log \left(1+\frac{K V^2}{g}\right) \\ \Rightarrow 2 g x=\frac{g}{K} \log \left(1+\frac{K V^2}{g}\right)-\frac{g}{K} \log \left(1+\frac{K}{g} v^2 \right) \\ \Rightarrow x=\frac{1}{2 g} \times \frac{g}{K} \log \left(\frac{1+\frac{K}{g} V^2}{1+\frac{K}{g} v^2}\right) \\ \Rightarrow x=\frac{1}{2 K} \log \left(\frac{1+\frac{K}{g} V^2}{1+\frac{K}{g} v^2}\right)
यदि कण द्वारा अधिकतम ऊँचाई h तय की जाती है तब x=h,v=0
\Rightarrow h=\frac{1}{2 K} \log \left(1+\frac{K}{g} V^2\right) \cdots(5)
जब कण अधिकतम ऊँचाई B पर पहुँचता है तो विरामावस्था से पुनः नीचे गिरना प्रारम्भ होता है।अतः समीकरण (2) से गति का समीकरण:
v \frac{d v}{d y}=g\left(1-\frac{K}{g} v^2\right) \\ \Rightarrow \frac{-2 v d v}{\left(1-\frac{K}{g} v^2 \right)}=-2 g d y
समाकलन करने पर:
\frac{g}{K} \log \left(1-\frac{K}{g} v^2\right)=-2 g y+A_2
प्रारम्भ में जब y=0 (उच्चतम ऊँचाई पर), v=0
A_2=0 \\ \Rightarrow-2 y=\frac{1}{K} \log \left(1-\frac{K}{g} v^2\right) \\ \Rightarrow y=-\frac{1}{2K} \log \left(1-\frac{K}{g} v^2\right) \cdots(6)
प्रक्षेप बिन्दु A पर लौटते समय कण का वेग V’ है तो y=h,v=V’
समीकरण (6) से:
h=-\frac{1}{2K} \log \left(1-\frac{K}{g} V^{\prime^2}\right) \cdots(7)
समीकरण (5) व (7) से:
\frac{1}{2 K} \log\left(1+\frac{K}{g} V^2\right)=-\frac{1}{2 K} \log \left(1-\frac{K}{g} V^{\prime^2} \right) \\ \Rightarrow \log \left(1+\frac{K}{g} V^2\right)+\log \left(1-\frac{k}{g} V^{\prime^2}\right)=0 \\ \Rightarrow \log \left(1+\frac{K}{g} V^2\right)\left(1-\frac{K}{g} V^{\prime^2}\right)=0 \\ \Rightarrow \left(1+\frac{K}{g} V^2\right)\left(1-\frac{K}{g} V^{\prime^2}\right)=1 \\ \Rightarrow 1+\frac{K}{g} V^2-\frac{K}{g} V^{\prime^2}-\frac{K^2}{g^2} v^2 V^{\prime^2}=1 \\ \Rightarrow \frac{K}{g} V^{\prime^2} +\frac{K^2}{g^2} v^2 V^{\prime^2}=\frac{K}{g} V^2 \\ \Rightarrow \frac{K}{g} V^{\prime^2} \left(1+ \frac{K}{g} V^2\right)=\frac{K}{g} V^2 \\ \Rightarrow \frac{1}{V^{\prime^2}}=\frac{1+\frac{K}{g} V^2}{V^2} \\ \Rightarrow \frac{1}{V^{\prime^2}}=\frac{1}{V^2}+\frac{K}{g}
Example:6.एक कण प्रति इकाई संहति के \mu गुने के बल के तहत एक बिंदु O से दूरी a पर विरामावस्था से चलता है;यदि जिस माध्यम में यह चलता है उसका प्रतिरोध वेग के वर्ग का k गुना है तो सिद्ध करो कि वेग का वर्ग, जब यह O से x दूरी पर होगा
\frac{\mu x}{k}-\frac{\mu a}{k} e^{2k(x-a)}+\frac{\mu}{2k^2}\left[1-e^{2k(x-a)}\right]
यह भी सिद्ध करो कि जब यह प्रथम बार विरामावस्था में आता है तो दूरी b होगी
\left(1-2bk \right) e^{2bk}=\left(1+2ak\right) e^{-2ak}
(A particle moves from rest at a distance a from a point O under the action of a force to O equal to \mu times the distance per unit of mass ;if the resistance of the medium in which it moves be k times the square of the velocity per unit mass. Show that the square of the velocity, when it is at a distance x from O, is \frac{\mu x}{k}-\frac{\mu a}{k} e^{2k(x-a)}+\frac{\mu}{2k^2}\left[1-e^{2k(x-a)}\right]
Show also that when it first comes to rest it will be at a distance b given by)
\left(1-2bk \right) e^{2bk}=\left(1+2ak\right) e^{-2ak}
Solution:O स्थिर बिन्दु है।माना कि कण बिन्दु A से प्रारम्भ होता है जहाँ OA=a.माना किसी समय कण की स्थिति P है जहाँ OP=x
P बिन्दु पर कण पर कार्यरत बल
(1.) m \mu x बल O की ओर (अर्थात् x घट रहा है)
(2.)प्रतिरोध बल mkv^2, O से दूर (x बढ़ने की ओर)
गति का समीकरण
m v \frac{d v}{d x}=-m \mu x+m k v^2 \\ \Rightarrow v \frac{d v}{d x}=-\mu x+k v^2 \\ \Rightarrow \frac{1}{2} \frac{d v^2}{d x}=-\mu x+k v^2 \\ \Rightarrow \frac{d v^2}{d x}-2 k v^2=-2 \mu x \cdots(1)
यह V^2 में रैखिक अवकल समीकरण है अतः
समाकलन गुणक (I. F.)=e^{\int-2 k d x}=e^{-2 k x}
e^{-2 k x}
समाकलन करने पर:
v^2 e^{-2 k x} =-2 \mu \int x e^{-2 k x} d x+C \\ =-2 \mu \left[\frac{x e^{-2kx}}{-2 k}-\int 1 \cdot \frac{e^{-2 k x}}{-2 k}\right]+C \\=-2 \mu \left[-\frac{x e^{-2 k x}}{2 k}-\frac{1}{4 k} e^{-2 k x}\right]+C \\ \Rightarrow v^2 =\frac{\mu x}{k}+\frac{\mu}{2 k^2}+C e^{2 k x}
A पर प्रारम्भ में ;v=0 जब x=a
\therefore C=-e^{-2 k a}\left(\frac{\mu a}{k}+\frac{\mu}{2 k^2}\right) \\ \therefore v^2=\frac{\mu x}{k}+\frac{\mu}{2 k^2}-e^{-2 a k}\left(\frac{\mu a}{k}+\frac{\mu}{2 k^2}\right) e^{2 k x} \\ v^2=\frac{\mu x}{k}-\frac{\mu a}{k} e^{2 k(x-a)}+\frac{\mu}{2 k^2}\left[1-e^{2 k(x-a)}\right]
माना O पर वेग है अर्थात् x=0
v_{1}^2=-\frac{\mu a}{k} e^{-2 a k}+\frac{\mu}{2 k^2}\left(1-e^{-2 k}\right) \\ =\frac{\mu}{2 k^2}-\frac{\mu}{k}\left(a+\frac{1}{2 k}\right) e^{-2 a k} \neq 0
अतः वेग O पर शून्य नहीं है।अतः कण O को पार करके O के दूसरी तरफ सरल रेखा AO तक गति करता है।माना B पर वेग शून्य हो जाता है अतः OB=b
अर्थात् x=-b,v=0 समीकरण (2) में रखने पर
0=-\frac{\mu b}{k}-\frac{\mu a}{k} e^{-2 k(b+a)}+\frac{\mu}{2 k^2}\left[1-e^{-2 k(b+a)}\right] \\ e^{2 k b} से गुणा करने पर:
0=-\frac{\mu b}{k} e^{2 b k}-\frac{\mu a}{k} e^{-2 a k}+\frac{\mu}{2 k^2} e^{2 k b}-\frac{\mu}{2 k^2} e^{-2 a k} \\ \Rightarrow (1-2 b k) e^{2 b k}=(1+2 a k) e^{-2 a k} [\frac{2 k^2}{\mu} से गुणा करने पर]
उपर्युक्त उदाहरणों के द्वारा प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium),वेग के समानुपाती प्रतिरोध के अधीन उर्ध्वाधर गति (Vertical Motion Under Resistance Proportional to Velocity) को समझ सकते हैं।
3.प्रतिरोधी माध्यम में सरल रेखीय गति के सवाल (Rectilinear Motion in Resisting Medium Questions):
(1.) kv^2 प्रति इकाई संहति वाले प्रतिरोधी माध्यम में एक कण सीधे ऊपर की ओर गतिमान है।सिद्ध कीजिए कि कण की उस बिन्दु से उच्चतम बिन्दु तक की ऊँचाई किसी समय होगी:
\frac{1}{k} \log \left[\sec t^{\prime} \sqrt{(g k)}\right]
जहाँ t’ कण के किसी बिन्दु से उच्चतम बिन्दु तक पहुँचने का समय है।
(If a particle is ascending vertically in a medium in which the resistance is kv^2 per unit mass.Show that its distance at any instance below the highest point of its path is :
\frac{1}{k} \log \left[\sec t^{\prime} \sqrt{(g k)}\right]
Where t’ denotes the time it will take to reach its highest point)
(2.)एक कण के प्रतिरोधी माध्यम जिसका प्रतिरोध वेग के वर्गानुपाती है,में गुरुत्वाकर्षण के अधीन U वेग से सीधे ऊपर की ओर फेंका जाता है।कण की गति का विवेचन करें।
(A particle is projected upwards with velocity U under gravity in a resisting medium due to which resistance varies as the square velocity.Discuss the motion of the particle)
उपर्युक्त सवालों को हल करने पर प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium),वेग के समानुपाती प्रतिरोध के अधीन उर्ध्वाधर गति (Vertical Motion Under Resistance Proportional to Velocity) को ठीक से समझ सकते हैं।
Also Read This Article:- Product of Inertia in Dynamics
4.प्रतिरोधी माध्यम में सरल रेखीय गति (Frequently Asked Questions Related to Rectilinear Motion in Resisting Medium),वेग के समानुपाती प्रतिरोध के अधीन उर्ध्वाधर गति (Vertical Motion Under Resistance Proportional to Velocity) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.प्रतिरोधी माध्यम में प्रतिरोध और वेग में क्या सम्बन्ध होता है? (What is the Relation Between Resistance and Velocity in a Resisting Medium?):
उत्तर:एक पिण्ड एक माध्यम जैसे जल,वायु इत्यादि में गति करे तो उसकी गति का प्रतिरोध होता है।ज्यों-ज्यों पिण्ड का वेग बढ़ता जाता है,त्यों-त्यों ही माध्यम के कारण प्रतिरोध बढ़ता जाता है,व्यापकतया (in general) यह प्रतिरोध गति का वेग फलन होता है।अल्प गति के लिए प्रतिरोध सन्निकटतः वेग के समानुपाती होता है।बड़ी वेग के लिए प्रतिरोध वेग के वर्ग के समानुपाती होता है और इससे बड़े वेग के लिए प्रतिरोध वेग के घन के समानुपाती होता है और इसी प्रकार अति बड़े वेग के लिए वेग की तीन से बड़ी घात के समानुपाती होता है।
प्रश्न:2.प्रतिरोधी माध्यम में चरम वेग को समझाइए। (Explain the Terminal Velocity in the Resisting Medium):
उत्तर:कण की गति का समीकरण
\frac{d^2 x}{d t^2}=\frac{d v}{d t}=g-k v^n=k\left(\frac{g}{k}-v^n\right)
जहाँ k समानुपाती अचर है तथा g गुरुत्वीय त्वरण है जो कि अचर (माना) रहता है।
उपर्युक्त समीकरण से स्पष्ट है कि कण का त्वरण घटता है जैसे-जैसे v का मान बढ़ता है और त्वरण शून्य हो जाता है तब v=\left(\frac{q}{k}\right)^{\frac{1}{n}}
यह कण का अधिकतम वेग है जिसे अन्तिम वेग (Terminal Velocity) अथवा सीमान्त वेग (चरम वेग) (Limited Velocity) कहते हैं अर्थात् इस वेग में कोई वृद्धि नहीं होती है और कण इसके पश्चात से चलता है।
प्रश्न:3.वेग के समानुपाती प्रतिरोध के अधीन गति के सूत्रों को लिखो। (Write the Formulae of Motion Under Resistance Proportional Velocity):
उत्तर: (1.) t=\frac{v}{g} \log \frac{V}{V-v}
(2.) x=V t+\frac{V^2}{g} \cdot\left[e^{\left(\frac{-g t}{V}\right)}-1\right]
(3.) x=\frac{v^2}{g} \cdot \log \frac{V}{V-v}-\frac{V}{g} v
V अन्तिम वेग है।
उपर्युक्त प्रश्नों के उत्तर द्वारा प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium),वेग के समानुपाती प्रतिरोध के अधीन उर्ध्वाधर गति (Vertical Motion Under Resistance Proportional to Velocity) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Rectilinear Motion in Resisting Medium
प्रतिरोधी माध्यम में सरल रेखीय गति
(Rectilinear Motion in Resisting Medium)
Rectilinear Motion in Resisting Medium
प्रतिरोधी माध्यम में सरल रेखीय गति (Rectilinear Motion in Resisting Medium) के
इस आर्टिकल में वेग के समानुपाती प्रतिरोध के अधीन उर्ध्वाधर गति पर आधारित सवालों को
हल करके समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.