Kepler Laws for Planetary Motion
1.ग्रहों की गति के लिए केप्लर के नियम (Kepler Laws for Planetary Motion):
ग्रहों की गति के लिए केप्लर के नियम (Kepler Laws for Planetary Motion):सुप्रसिद्ध डेनिस ज्योतिषी केप्लर (1571-1630) ने सौर परिवार के ग्रहों की गति के लिए कुछ आनुभविक निम्न नियमों का प्रतिपादन किया:
(1.) प्रत्येक ग्रहों की कक्षाएं दीर्घवृत्त के रूप की है जिनकी एक नाभि पर सूर्य स्थित है।
(Each planet describe an ellipse with the sun as one of the foci.)
(2.)सूर्य से ग्रह तक खींची हुई ध्रुवान्तर रेखाओं की गति से कक्षा समतल में रचित क्षेत्रफल समान समयों में समान होता है।
(The areas described by the radii drawn from the planet to the sun in the same orbit, proportional to the times of describing them.)
(3.)विभिन्न ग्रहों के परिक्रमण काल का वर्ग उनकी कक्षाओं के दीर्घाक्षों के घन के समानुपाती होता है।
(The squares of the periodic times of the planets are proportional to the cubes of the semi major axis of their orbits.)
केप्लर के नियमों से न्यूटन द्वारा किए गए निगमन:
(1.)प्रथम नियम से सभी ग्रहों की कक्षाएं दीर्घवृत्ताकार है इसलिए यह निष्कर्ष निकालते हैं कि प्रत्येक ग्रह का त्वरण अर्थात् इस पर कार्यशील बल सूर्य से दूरी के वर्ग के व्युत्क्रमानुपाती होता है।
(2.)द्वितीय नियम से स्पष्ट है कि क्षेत्रीय वेग (Areal Velocity) अचर रहता है अर्थात्
r^{2} \dot{\theta}=अचर \Rightarrow \frac{1}{r} \frac{d}{d t}\left(r^{2} \dot{\theta}\right)=0
जिससे ग्रहों का अनुप्रस्थ त्वरण (Transverse acceleration) शून्य होता है अर्थात् प्रत्येक ग्रह सर्वदा कक्षा के ध्रुव (नाभि) जिस पर सूर्य स्थित है,की ओर आकर्षित होता है।
(3.)यदि किसी ग्रह का कार्यशील बल प्रति इकाई संहति \frac{\mu}{r^{2}} हो,परिक्रमण काल T हो और दीर्घवृत्तीय कक्षा का अर्द्ध दीर्घाक्ष a हो तो हम जानते हैं कि
T=\frac{2 \pi}{\sqrt{\mu}} a^{\frac{3}{2}} \\ \Rightarrow T^{2}=\frac{4 \pi^{2}}{\mu} \cdot a^{3}
अब केप्लर के तृतीय नियम के अनुसार ग्रह के लिए \frac{4 \pi^{2}}{\mu} अचर है।अतः प्रत्येक ग्रह के लिए \mu (सूर्य से इकाई दूरी पर त्वरण) अचर है।अतः सिद्ध होता है कि विभिन्न ग्रहों पर सूर्य का आकर्षण बल उन ग्रहों की गति की संहति के समानुपाती (Proportional) होते हैं।
न्यूटन ने लगभग एक शताब्दी बाद केप्लर के नियमों से सार्वत्रिक गुरुत्वाकर्षण नियम (Universal Law of Gravitation) का निगमन किया।जिसका प्रकथन है कि समष्टि (Universe) में प्रत्येक कण प्रत्येक अन्य कण को एक ऐसे बल से आकर्षित करता है जो उन कणों की संहतियों के गुणनफल के समानुपाती तथा उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है अर्थात् यदि दो कणों की संहतियां क्रमशः m_{1} तथा m_{2} है तथा उनके बीच दूरी r हो तो उनके बीच का आकर्षण बल \gamma=\frac{m_{1} m_{2}}{r^{2}} ; जहां \gamma अचर है जिसे गुरुत्वाकर्षण अचरांक कहते हैं।
दीर्घवृत्त के लिए कुछ महत्त्वपूर्ण परिणाम (Some Important Results of Ellipse):
(1.) दीर्घवृत्त पर स्थित किसी बिन्दु P की नाभिक दूरियों का योग अचर होता है तथा यह दीर्घाक्ष की लम्बाई (=2a) के बराबर होता है अर्थात्
SP+HP=2a
यदि SP=r,तब HP=2a-r
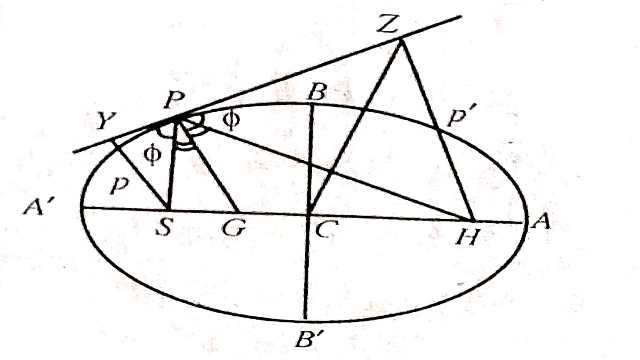
(2.)यदि दीर्घवृत्त के किसी बिन्दु पर खींची गई स्पर्शरेखा पर उसकी दोनों नाभियों से डाले गए लम्बों का गुणनफल अचर होता है तथा अर्द्ध लघुअक्ष के वर्ग के बराबर होता है।
PP'=SY.HZ=b^{2}
(3.)CZ समान्तर SP
(4.) दीर्घवृत्त का नाभिलम्ब=\frac{2 b^{2}}{a}=2 l जहां, b^{2}=a^{2}\left(1-e^{2}\right) ,जहां a अर्द्ध-दीर्घाक्ष,b अर्द्ध-लघुअक्ष तथा e उत्केन्द्रता है।
(5.)CH=CS=se
(6.) \angle YPS=\angle ZPH या \angle GPS=\angle GPH जहां बिन्दु P पर YPZ स्पर्शरेखा तथा PG अभिलम्ब है।
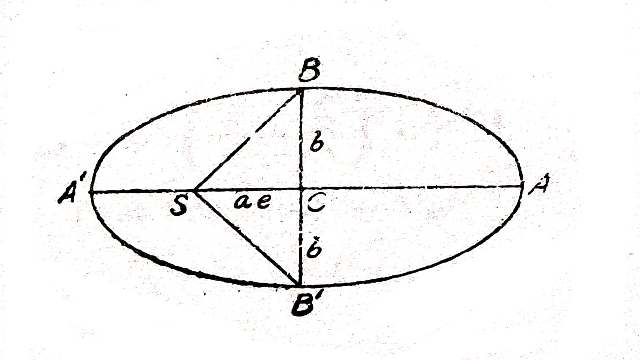
(7.)A(a,0),A'(-a,0),B(0,b),B'(0,-b),S(-ae,0),H(ae,0)
H B^{2}=a^{2} e^{2}+b^{2}=a^{2} \Rightarrow H B=a
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:–Central Orbit Dynamics
2.ग्रहों की गति के लिए केप्लर के नियम के उदाहरण (Kepler Laws for Planetary Motion Examples):
Example:1.सूर्य के चारों ओर घूमने में पृथ्वी की कक्षा की उत्केन्द्रता \frac{1}{60} है;प्रदर्शित करो कि सूर्य से पृथ्वी की दूरी,कक्षा की अर्ध-दीर्घाक्ष की लम्बाई से अर्द्ध-वर्ष से लगभग दो दिन अधिक तक ज्यादा रहेगी।
(The eccentricity of the earth’s orbit round the sun is \frac{1}{60}; show that the earth’s distance from the sun exceeds the length of the semi major axis of the orbit during about 2 days more than half the year.)
Solution:-h=r^{2} \frac{d \theta}{d r}=2 (संकेन्द्र कक्षा क्षेत्रफल निर्माण की दर अचर)
यदि t त्रिज्या खण्डीय क्षेत्रफल SB’ABS के निर्माण में लिया गया समय हो अर्थात् सूर्य द्वारा B’AB से आधा
क्षेत्रफल निर्माण की दर=\frac{\text{Area SB'ABS}}{t} \cdots(1)
पुनः पृथ्वी सूर्य के चारों ओर दीर्घवृत्त में एक वर्ष में पूरा एक चक्कर लगाती है
अतः क्षेत्रफल निर्माण की दर=\frac{\text{Area of ellipse}}{\text{one Year}} \cdots(2)
क्षेत्रफल निर्माण की दर अचर है इसलिए समीकरण (1) व (2) से-
\frac{\text{Area SB'ABS}}{t}=\frac{\text{Area of ellipse}}{\text{one Year}}
SB’ABS का क्षेत्रफल=ABB’ का क्षेत्रफल+\triangle SBB' \text{ का क्षेत्रफल } \\ =\frac{\pi a b}{2}+\frac{1}{2}(2 b)(a e)\cdots(3)
[दीर्घवृत्त का क्षेत्रफल=\pi a b]
समीकरण (3) से-
t =\frac{\frac{\pi a b}{2}+\text { abe }}{\pi a b} \times \text { oneyear } \\ =\left(\frac{1}{2}+\frac{e}{\pi}\right) \text { one year } \\ =\frac{1}{2} \text { year } +\frac{1}{60} \cdot \frac{7}{22} \times 365 \text { days } \\ \Rightarrow t =\frac{1}{2} \text { year }+2 \text { day nearly }
Example:2.यदि एक कण नाभि से r दूरी पर है,इसका वेग v की दिशा ध्रुवान्तर रेखा से कोण बनाती है तो सिद्ध कीजिए कि
e^{2} \mu^{2}=\left(v^{2} r-\mu\right)^{2} \sin ^{2} \phi +\mu^{2} \cos ^{2} \phi
(Prove that if when the particle is at a distance r from the focus,its velocity is v in a direction making an angle with the radius vector,then prove that
e^{2} \mu^{2}=\left(v^{2} r-\mu\right)^{2} \sin ^{2} \phi +\mu^{2} \cos ^{2} \phi
Solution:जब p= r \sin \phi तो vp=h
v r \sin \phi=h \cdots(1) \\ \Rightarrow h^{2}=\mu l=\mu \frac{b^{2}}{a} \\ \Rightarrow h^{2} =\mu a \left(1-e^{2}\right) \cdots(2)
समीकरण (1) व (2) से-
v^{2} r^{2} \sin ^{2} \phi=\mu a\left(1-e^{2}\right) \\ \Rightarrow \frac{1}{a}=\frac{\mu\left(1-e^{2}\right)}{v^{2} r^{2} \sin ^{2} \phi} \cdots(3) \\ v^{2}=\mu\left(\frac{2}{r}-\frac{1}{a}\right) \cdots(4)
समीकरण (3) से \frac{1}{a} का मान समीकरण (4) में रखने पर-
v^{2}=\frac{2 \mu}{r}-\mu \cdot \frac{\mu\left(1-e^{2}\right)}{v^{2} r^{2} \sin ^{2} \phi} \\ \Rightarrow \left(\frac{v^{2} r-2 \mu}{r}\right) v^{2} r^{2} \sin ^{2} \phi=-\mu^{2}+\mu^{2} e^{2} \\ \Rightarrow e^{2} \mu^{2} =\left(v^{4} r^{2}-2 \mu v^{2} r\right) \sin^{2} \phi+\mu^{2}\left(\cos ^{2} \phi+\sin ^{2} \phi\right) \\ =\left(v^{4} r^{2}-2 \mu v^{2} r+\mu^{2}\right) \sin ^{2} \phi+\mu^{2} \cos ^{2} \phi \\ =\left(v^{2} r-\mu \right)^{2} \sin ^{2} \phi+\mu^{2} \cos ^{2} \phi \\ \Rightarrow e^{2} \mu^{2} =\left(v^{2} r-\mu\right)^{2} \sin ^{2} \phi+\mu^{2} \cos ^{2} \phi
Example:3.यदि किसी ग्रह को अपनी कक्षा (वृत्तीय माने जाने वाली) में एकाएक रोक दी जाए,तो सिद्ध कीजिए कि वह ग्रह के परिक्रमण काल \frac{\sqrt{2}}{8} के गुणा समय में सूर्य के अन्दर गिर जाएगा।
(If a planet was suddenly stopped in the orbit, supposed circular,show that if would fall into the sun in a time which is \frac{\sqrt{2}}{8} times the period of the planet's revolution.)
Solution:माना कण के सापेक्ष वृत्तीय कक्षा में घूम रहा है तथा अचानक P पर रूक जाता है ताकि इसका वेग घटकर शून्य हो जाए तथा अब यह S की तरफ चलना प्रारम्भ करता है जहां PS सरल रेखा है।
गति का समीकरण
\frac{d^{2} x}{d t^{2}}=-\frac{\mu}{x^{2}} (x घट रहा है)
\Rightarrow \frac{d v}{d x}=-\frac{\mu}{x^{2}} \\ \Rightarrow v d v=-\frac{\mu}{x^{2}} d x \\ \Rightarrow \int v d v=-\int \frac{\mu}{x^{2}} d x \\ \Rightarrow v^{2}=\frac{2 \mu}{x}+A
जब x=a तो ग्रह P पर है तब v=0
A=-\frac{2 \mu}{a} \\ v^{2} =2 \mu\left(\frac{1}{x}-\frac{1}{a}\right) \\ =2 \mu\left(\frac{a-x}{a x}\right) \\ \Rightarrow v=\frac{d x}{d t}= -\sqrt{(2 \mu)} \sqrt{\frac{(a-x)}{a x}} \\ \Rightarrow \int_{a}^{0} \sqrt{\left(\frac{ax}{a-x}\right)} d x=\int_{t=0}^{t} \sqrt{(2 \mu)} d t \cdots (1)
सीमाएं- t=0 तब x=a=SP
जब t=t. तब x=0 अर्थात् ग्रह S पर है।
\text { putting } x=a \cos ^{2} \theta \Rightarrow d x=-2 a \cos \theta \sin \theta d \theta \\ \int_{0}^{\frac{\pi}{2}} \sqrt{a} \frac{\cos \theta}{\sin \theta} 2 a \cos \theta \sin \theta d \theta=\sqrt{(2 \mu)}t \\ \Rightarrow 2 a^{\frac{3}{2}} \int_{0}^{\frac{\pi}{2}} \cos ^{2} \theta d \theta=\sqrt{(2 \mu)} t \\ \Rightarrow t=\frac{2 a^{\frac{3}{2}}}{\sqrt{(2 \mu)}} \cdot \frac{1}{2} \cdot \frac{\pi}{2}
ग्रह का आवर्तकाल T है तब
T=\frac{2 \pi}{\sqrt{\mu}} a^{\frac{3}{2}} \\ \Rightarrow t=\frac{1}{4 \sqrt{2}} T \Rightarrow t=\left(\frac{\sqrt{2}}{8}\right) T
Example:4.यदि किसी ग्रह का परिक्रमण काल 365 दिन है और उत्केन्द्रता e=\frac{1}{60} हो तो सिद्ध करो कि उन अर्ध भागों की रचना करने के समय जो बलकेन्द्र से गुजरने वाली नाभिलम्ब द्वारा परिबद्ध होते हैं,लगभग \frac{365}{2}\left[1 \pm \frac{1}{15 \pi}\right] होंगे।
(If the period of planet be 365 days and the eccentricity e is \frac{1}{60} ;show that the times of describing the two halves of the orbit,bounded by the latus rectum passing through the centre of force are \frac{365}{2}\left[1 \pm \frac{1}{15 \pi}\right]
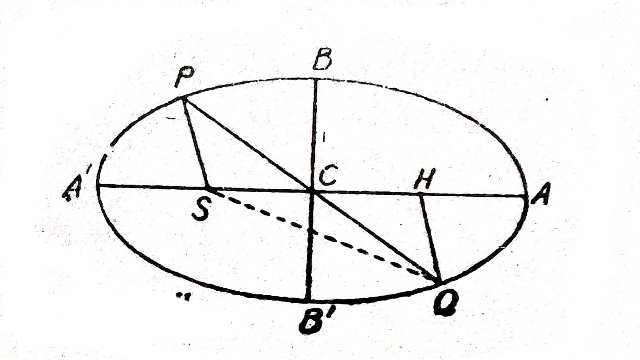
Solution:किसी दीर्घवृत्तीय चाप LAL' के निर्माण में लगा समय
T=\frac{2 a^{\frac{3}{2}}}{\sqrt{\mu}}\left[2 \tan^{-1} \sqrt{\left(\frac{1-e}{1+e}\right)} \tan \frac{\theta}{2}-e \sqrt{1-e^{2}} \frac{\sin \theta}{1+e \cos \theta}\right]
नाभिलम्ब पर \theta=90^{\circ}
T_{1}=\frac{2 a^{\frac{3}{2}}}{\sqrt{\mu}}\left[2 \tan^{-1} \sqrt{\left(\frac{1-e}{1+e}\right)}- e \sqrt{\left(1-e^{2}\right)}\right]
e=\frac{1}{60} बहुत छोटा है अतः e की उच्चतम घातों को उपेक्षणीय मानने पर
आवर्तकाल T=\frac{2 \pi}{\sqrt{\mu}} a^{\frac{3}{2}}=365 दिन
T_{1} =\frac{T}{\pi}\left[2 \tan ^{-1} (1-e)^{\frac{1}{2}}\left(1+e\right)^{-\frac{1}{2}}-e\left(1-e^{2}\right)^{\frac{1}{2}}\right]\\ =\frac{T}{\pi}\left[2 \tan^{-1} \left(1-\frac{1}{2} e \cdot \cdots\right)\left(1-\frac{1}{2} e \cdots\right)-e\left(1-\frac{1}{2} e^{2} \cdots\right)\right] \\ =\frac{T}{\pi}\left[2 \tan ^{-1}(1-e)-e\right] \\ \tan^{-1} (1)=\frac{\pi}{4} \Rightarrow \tan ^{-1}(1-e)=\frac{\pi}{4}-z जहां z छोटा है
1-e=\tan \left(\frac{\pi}{4}-z\right)=\frac{1-\tan z}{1+\tan z} \\ \Rightarrow 1-e =(1-\tan z)(1+\tan z)^{-1} \\ =(1-\tan z)(1-\tan z \cdots) \\ =(1-2 \tan z \cdots) \\ \tan z =\frac{e}{2}=\frac{1}{120} \\ \therefore z =\tan^{-1} \left(\frac{1}{120}\right)=\frac{1}{120}(लगभग )
T_{1} =\frac{T}{\pi}\left[2\left(\frac{\pi}{4}-z\right)-\frac{1}{60}\right] \\ =\frac{T}{\pi}\left[\frac{\pi}{2}-\frac{1}{60}-\frac{1}{60}\right] \\ T_{1} =\frac{T}{2}\left(1-\frac{1}{15 \pi}\right)(लगभग )
T_{2} चाप L'A'L है अतः
T_{2}=T-T_{1}=T-\frac{1}{2}\left(1-\frac{1}{15 \pi}\right) \\ \Rightarrow T_{2}=\frac{T}{2}\left(1+\frac{1}{15 \pi}\right)
अतः T_{1} तथा T_{2} का मान
\frac{T}{2}\left(1 \pm \frac{1}{15 \pi}\right)=\frac{365}{2}\left(1 \pm \frac{1}{15 \pi} \right)
Example:5.प्रदर्शित कीजिए कि यदि एक कण केन्द्रीय बल के अधीन गति करता है जो कि दूरी के वर्ग व्युत्क्रमानुपाती है तो किसी भी त्रिज्या वाली वृत्तीय कक्षा में किसी बिन्दु पर वेग और उसी बल के अधीन अनन्त दूरी से उस बिन्दु तक गिरने से प्राप्त वेग का अनुपात 1: \sqrt{2} है।
(Show that if a particle moves under a central force inversely proportional to the square of distance,the velocity at any point of a circular orbit of any radius and under the same force the velocity acquired in falling from infinity so that point are in the ratio 1: \sqrt{2})
Solution:एक वृत्त के निर्माण में वेग v_{2} हो तब
\frac{v_{2}^{2}}{R}=Normal acceleration (अभिलाम्बिक त्वरण)=\frac{2 \mu}{R^{2}}
\Rightarrow v_{2}^{2}=\frac{\mu}{R}=\frac{1}{2} \cdot\left(\frac{2 \mu}{R}\right) \\ \Rightarrow v_{2}^{2}=\frac{1}{2} v_{1}^{2}\left[\because v_{2}=\frac{2 \mu}{R}\right] \\ \Rightarrow v_{2}=\frac{1}{\sqrt{2}} v_{1} \\ \Rightarrow v_{2}: v_{1}=1: \sqrt{2}
Example:6.यदि पृथ्वी का वेग उसकी कक्षा (वृत्तीय मानकर) के किसी बिन्दु पर लगभग आधा और बढ़ा दिया जाए तो सिद्ध करो कि वह सूर्य को नाभि मानकर एक परवलय में चलेगी।
(If the velocity of the earth of any point of its orbit assumed that it would describe a parabola about the sun as focus)
Solution:यदि लघुअक्ष के किनारे पर वेग v है
SB=a तब V^{2}=\mu \left(\frac{2}{a}-\frac{1}{a}\right)=\frac{\mu}{a} \cdots(1)
जब गतिज ऊर्जा (K.E.) दुगुनी है तो माना वेग v है
तब \frac{1}{2} m v^{2}=2\left(\frac{1}{2} m V^{2}\right) \\ \Rightarrow v^{2}=2 V^{2} \\ \Rightarrow v^{2}=2 \frac{\mu}{a} [(1) से ]
परन्तु हम जानते हैं परवलय कक्षा के लिए v^{2}=\frac{2 \mu}{r}=\frac{2 \mu}{a} (\because r=a)
अतः कण एक परवलय कक्षा का निर्माण करता है।
उपर्युक्त उदाहरणों के द्वारा ग्रहों की गति के लिए केप्लर के नियम (Kepler Laws for Planetary Motion) को समझ सकते हैं।
3.ग्रहों की गति के लिए केप्लर के नियम की समस्याएं (Kepler Laws for Planetary Motion Problems):
(1.)एक कण एक बल जो कि \frac{\mu}{\text{ दूरी}^{2}} है और नाभि की ओर है,के अधीन एक दीर्घवृत्त का निर्माण करता है।यदि इसे एक नियत बिन्दु से,जिसकी दूरी बलकेन्द्र से r है,v वेग से प्रक्षिप्त किया गया हो तो सिद्ध कीजिए कि इसका आवर्तकाल होगा:
(A particle descibes an ellipse under a force \frac{\mu}{\text{distance }^{2}} towards the focus;if it was projected with velocity V from a point distant r from the centre of force, show that its periodic time is:)
\frac{2 \pi}{\sqrt{\mu}}\left[\frac{2}{r}-\frac{V^{2}}{\mu}\right]^{-\frac{3}{2}}
(2.) एक कण केन्द्रीय त्वरण \frac{\mu}{r^{2}} से गतिमान है इसे R दूरी पर V वेग से प्रक्षिप्त किया जाता है,यदि प्रक्षेप कोण निम्न हो:
(A particle moving with a central acceleration \frac{\mu}{r^{2}} is projected with velocity V at a distance R show that the path is a rectangular hyperbola if the angle of projection is:
\sin^{-1}\left[\frac{\mu}{V R\left(v^{2}-\frac{2 \mu}{R}\right)^{\frac{1}{2}}}\right]
उपर्युक्त सवालों को हल करने पर ग्रहों की गति के लिए केप्लर के नियम (Kepler Laws for Planetary Motion) को ठीक से समझ सकते हैं।
Also Read This Article:-Find Central Force For Central Orbit
4.ग्रहों की गति के लिए केप्लर के नियम (Kepler Laws for Planetary Motion) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.केप्लर के ग्रह गति के 3 नियम क्या हैं? (What are Kepler 3 laws of planetary):
उत्तर:वास्तव में तीन हैं,केप्लर के नियम जो ग्रहों की गति के हैं: (1)प्रत्येक ग्रह की कक्षा एक दीर्घवृत्त है जिसमें सूर्य एक फोकस पर है।(2.)सूर्य और ग्रह को मिलाने वाली रेखा समान समय में समान क्षेत्रफलों को पार करती है।और (3.) किसी ग्रह की कक्षीय अवधि का वर्ग उसके अर्द्ध-दीर्घाक्ष के घन के समानुपाती होता है।
प्रश्न:2.केप्लर का ग्रह गति का पहला नियम क्या है? (What is Kepler 1st Law of planetary motion?):
उत्तर:केप्लर का पहला नियम: सूर्य के सापेक्ष प्रत्येक ग्रह की कक्षा एक दीर्घवृत्त है।सूर्य का केंद्र हमेशा कक्षीय दीर्घवृत्त के एक फोकस पर स्थित होता है।सूर्य एक फोकस पर है।ग्रह अपनी कक्षा में दीर्घवृत्त का अनुसरण करता है,जिसका अर्थ है कि ग्रह से सूर्य की दूरी लगातार बदल रही है क्योंकि ग्रह अपनी कक्षा के चारों ओर घूमता है।
प्रश्न:3.केप्लर का नियम कक्षा 11 क्या है? (What is Kepler law class 11?), ग्रहों की गति का केप्लर का नियम कक्षा 11 (kepler law of planetary motion class 11):
उत्तर:केप्लर की कक्षाओं का नियम
इसमें कहा गया है कि,"सभी ग्रह सूर्य के चारों ओर अंडाकार कक्षा में घूमते हैं और सूर्य फोकस पर मौजूद होता है।"सूर्य के चारों ओर ग्रह द्वारा खोजे गए दीर्घवृत्त के लिए,निकटतम बिंदु को उपसौर (perihelion) कहा जाता है जबकि सबसे दूर के बिंदु को अपसौर (aphelion) कहा जाता है।
प्रश्न:4.केप्लर का तीसरा नियम समीकरण क्या है? (What is Kepler 3rd law equation?):
उत्तर:केप्लर का तीसरा नियम: T^{2}= \frac{2πr^{3}}{GM}
केप्लर का तीसरा नियम एक गणितीय सूत्र है।इसका मतलब है कि यदि आप किसी ग्रह की कक्षा की अवधि (T=सूर्य के चारों ओर चक्कर लगाने में ग्रह को कितना समय लगता हैं) जानते हैं, तो आप उस ग्रह की सूर्य से दूरी (r=ग्रह की कक्षा की अर्द्ध-दीर्घाक्ष ) निर्धारित कर सकते हैं।
प्रश्न:5.न्यूटन के 3 नियम क्या हैं? (What are the 3 Newton law?):
उत्तर:पहले नियम में, कोई वस्तु अपनी गति को तब तक नहीं बदलेगी जब तक कि उस पर कोई बल कार्य न करे।दूसरे नियम में, किसी वस्तु पर लगने वाला बल उसके त्वरण के द्रव्यमान गुणा के बराबर होता है।तीसरे नियम में, जब दो वस्तुएं परस्पर क्रिया करती हैं,तो वे समान परिमाण और विपरीत दिशा में एक-दूसरे पर बल लगाती हैं।
प्रश्न:6.केप्लर के प्रथम नियम को क्या कहते हैं ? (What is Kepler first law called?):
उत्तर:Kepler First law – The Law of Orbits | केप्लर के पहले नियम का अर्थ है कि ग्रह सूर्य के चारों ओर अण्डाकार कक्षाओं में घूमते हैं।एक दीर्घवृत्त एक आकृति है जो एक चपटा वृत्त जैसा दिखता है।वृत्त कितना चपटा है, यह उसकी उत्केन्द्रता से व्यक्त होता है।उत्केंद्रता 0 और 1 के बीच की एक संख्या है।यह एक पूर्ण वृत्त के लिए शून्य है।
प्रश्न:7.ग्रहों की गति का केप्लर का नियम सूत्र (kepler law of planetary motion formula):
उत्तर:केप्लर के ग्रहों की गति के लिए नियम दिए हैं उसके निम्नलिखित सूत्र हैं-
प्रथम नियम:- r_{min}+r_{max}= 2a × (length of major axis of an ellipse)
दूसरा नियम:-\frac{ΔA}{Δt}=constant
तीसरा नियम:-T^{2}= \frac{2πr^{3}}{GM}
प्रश्न:8.केप्लर का दूसरा नियम समीकरण (kepler second law equation):
उत्तर:क्षेत्रीय वेग = \frac{ΔA}{Δt}=constant ।चूँकि कोणीय संवेग अचर है,इसलिए क्षेत्रीय का वेग भी अचर होना चाहिए।यह ठीक केप्लर का दूसरा नियम है।
प्रश्न:9.केप्लर का तीसरा नियम सूत्र (kepler third law formula):
उत्तर:केप्लर का तीसरा नियम
समीकरण हमें पृथ्वी के परितः r त्रिज्या की वृत्ताकार कक्षा की अवधि बताता है:T^{2}= \frac{2πr^{3}}{GM} ।एक वृत्ताकार कक्षा के लिए,अर्द्ध-दीर्घाक्ष (r) कक्षा की त्रिज्या के समान है।
प्रश्न:10.ग्रहों की गति का केप्लर का नियम कक्षा 9 (kepler law of planetary motion class 9):
उत्तर:केप्लर के ग्रहों की गति के तीन नियमों को इस प्रकार बताया जा सकता है: (1) सभी ग्रह अण्डाकार कक्षाओं में सूर्य के चारों ओर घूमते हैं,जिसमें सूर्य एक केंद्र के रूप में होता है।(2)किसी भी ग्रह को सूर्य से ध्रुवान्तर रेखा समान समयावधि में समान क्षेत्रफलों को पार कर जाता है।केप्लर का ग्रहों की गति का दूसरा नियम।
उपर्युक्त प्रश्नों के उत्तर द्वारा ग्रहों की गति के लिए केप्लर के नियम (Kepler Laws for Planetary Motion) के बारे में जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |