Mathematical Theory of Everything
1.हर चीज का गणितीय सिद्धांत का परिचय (Introduction to Mathematical Theory of Everything):
- हर चीज का गणितीय सिद्धांत (Mathematical Theory of Everything) का तात्पर्य है कि इस संसार में परमात्मा के अलावा सब अपूर्ण हैं।पूर्ण ब्रह्म है।सृष्टि,विकास तथा अन्य अनेक परिवर्तनों के बावजूद परमात्मा की पूर्णता अखण्डित है अर्थात् कभी नष्ट नहीं होती है।यह सारा जगत पूर्ण है,पूर्ण से पूर्ण विकसित हो रहा है।पूर्ण से पूर्ण निकाल लेने पर भी पूर्ण ही शेष रहता है।उस पूर्ण की कोई सीमा नहीं है।पूर्ण को न तो तोड़ा जा सकता है और न उसे घटाया जा सकता है।गणित में उसे अनन्त कहा गया है अर्थात् जिसका कोई अन्त नहीं है.उसका वर्णन करना हमारे लिए असम्भव है।जो चराचर जगत में जो कुछ भी घटित हो रहा है वह उस पूर्ण में ही घटित हो रहा है। जो भी प्रकट होता है उस पूर्ण से ही प्रकट होता है और जो भी अप्रकट,अदृश्य होता है उसी पूर्ण में विलीन हो जाता है।पूर्ण में न कुछ जोड़ा जा सकता है और न कुछ घटाया जा सकता है।न पूर्ण के टुकड़े कर सकते हैं,न पूर्ण में से कुछ निकाला जा सकता है।पूर्ण को हम हिन्दी में सबकुछ भी कहते हैं,अंग्रेजी में Total, Everything तथा infinite भी कहते हैं।वेदो में उसे पूर्ण कहा गया है जो कि सकारात्मक तरीका(positive way) है तथा भगवान् बुद्ध ने उसे शून्य कहा है जो कि नकारात्मक तरीका है।शून्य को परिभाषित किया जाए तो उसकी परिभाषा है कि न तो शून्य की कोई सीमा होती है, न शून्य में कुछ मिलाया अर्थात् जोड़ा जा सकता है,न शून्य में से कुछ निकाला जा सकता है अर्थात् न शून्य में कुछ घटाया जा सकता है,न शून्य के टुकड़े कर सकते हैं।इस प्रकार पूर्ण positive तरीका है जबकि शून्य Negative तरीका है दोनों को मिला दिया जाए तो उसे ही हम परमात्मा,वाहे गुरू, God,अल्ला आदि नामों से पुकारते हैं।
In other words becoming large beyond any fixed bound.Total,everything is include in infinity. - आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:one plus one what makes this one
2.हर चीज का गणितीय सिद्धांत (Mathematical theory of everything):
- हम उन गणित की चीजों का प्रबंधन कैसे करते हैं जिन्हें हम वास्तव में नहीं समझते हैं जैसे कि गणित? क्या हम उससे आगे जा सकते हैं? क्या गणित सब कुछ और कुछ भी वर्णन करने में सक्षम है।यही वह सवाल है जिसका जवाब मैं आज देने की कोशिश करूंगा।
- नोट: मैं आपको इस पुस्तक को पढ़ने की भी सलाह देता हूं: गणितीय सिद्धांत का संचार
इससे पहले कि हम शुरू करें मुझे आपसे एक प्रश्न पूछना चाहिए; जब कुछ लोग “गणित” कहते हैं, तो आपके दिमाग में सबसे पहले क्या आता है? 1, 2, 3, 4, 5 जैसी संख्याएँ? एक गुणा, एक विभाजन, एक समीकरण? यह सब अच्छा सामान है,लेकिन बात यह है कि गणित ही नहीं है। यह सिर्फ गणित की भाषा है। हालाँकि, आज हम जिस गणित की भाषा का उपयोग करते हैं वह बसंत नहीं है। यह पिछले प्रकार की गणितीय भाषाओं का विकास है। - वेहद सुमेरियन गणित,मय गणित,मिस्र का गणित,रोमन गणित। गणित के सभी प्रकार जो आज हम उपयोग करते हैं, गणित की भाषा में विकसित हो रहे हैं। लेकिन हमारी गणित की भाषा अनिवार्य रूप से गणित की सबसे अच्छी भाषा नहीं है, लेकिन जो बात इसे इतना अच्छा बनाती है वह यह है कि यह गणित और मेडिकल विवरणों की परतों का वर्णन करने में आसान है। और यह मानक है। यदि आप उस गणितीय भाषा को दिखाना चाहते हैं, जिसका उपयोग हम आज किसी भी ग्रह पर करते हैं, तो वे एक रूप में या किसी अन्य को समझेंगे कि आप क्या कह रहे हैं।
Also Read This Article:Theory of everything
3.गणित गणित है(Math is math):
- यह एक ग्राफ है जो आपको गुदा दबाव और पेंगुइन डोडो की चिपचिपाहट के बीच संबंध दिखाता है
यदि तुम एक विदेशी सभ्यता, या ब्रह्मांड में कहीं एक उन्नत कृत्रिम बुद्धि इकाई का निरीक्षण करने के लिए थे, तो आप शायद यह पता लगा लेंगे कि वे गणितीय गुणों का वर्णन करने के लिए एक अलग तरीके का उपयोग कर रहे हैं। लेकिन यह वास्तव में मायने नहीं रखता है। जब तक उनका वर्णन सटीक है और वे एक ही बात का वर्णन कर रहे हैं कि हर कोई वर्णन करने की कोशिश कर रहा है, वे उसी परिणाम के साथ आएंगे। - उदाहरण के लिए, यह वह समीकरण है जिसका उपयोग हम किसी वस्तु के वेग का वर्णन करने के लिए करते हैं।
- Velocity=Displacement/Time
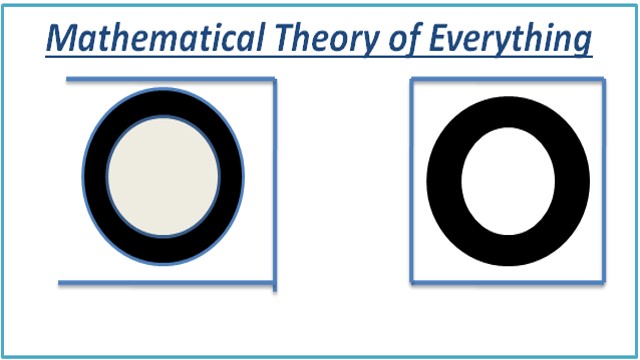
- बाईं ओर नीचे की छवि वह हो सकती है जो एक विदेशी सभ्यता किसी वस्तु के वेग का वर्णन करने के लिए उपयोग करेगी, या दाईं ओर नीचे की छवि वह हो सकती है जहां एक मजबूत कृत्रिम बुद्धि इकाई किसी वस्तु के वेग का वर्णन करने के लिए उपयोग करेगी। यह वास्तव में कोई बात नहीं है। जब तक विवरण सटीक है, तब तक वे सभी समीकरण समान परिणाम के साथ आएंगे।
- यह सब कुछ कवर करता है, यह “P” को कवर करता है,यह उन समीकरणों को कवर करता है जो आपने अब तक देखे हैं,यह आइंस्टीन के सामान्य सापेक्षता के सिद्धांत को कवर करता है,यह क्वांटम यांत्रिकी को कवर करता है,यह सब कुछ और किसी भी चीज को कवर करता है।
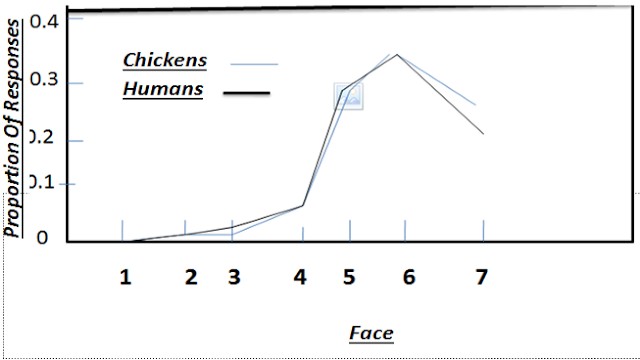
- यह एक और ग्राफ है जो आपको सुंदर मानव चेहरों के लिए मनुष्यों की वरीयताओं और सुंदर मानव चेहरों के लिए मुर्गियों की वरीयताओं के बीच अंतर दिखाता है।
- क्यों हम किसी वस्तु के वेग का वर्णन करने के लिए सूत्र के विस्थापन और समय का उपयोग करते हैं। यह एकमात्र तरीका नहीं है कि इसका वर्णन किया जा सके। बात हमारी अपनी गणितीय भाषा में भी है, हम जिस वेग के लिए समीकरण का उपयोग करते हैं, वह एकमात्र तरीका नहीं है जिसे स्वयं वर्णित किया जा सकता है।
- उदाहरण के लिए, हम वेग समीकरण का उपयोग यह बताने के लिए कर सकते हैं कि आप कितनी तेजी से बाइक पर जा रहे हैं। या आप यह वर्णन कर सकते हैं कि आप और बाइक 14 ऑक्टिलियन परमाणुओं से कैसे बने हैं, एक प्रणाली के रूप में एक साथ चलने के लिए एक दूसरे के साथ बातचीत करते हैं। एक और तरीका है कि आप इसे कर सकते हैं।
Also Read This Article:achieve mathematical maturity
4.गणितीय विवरण भयावह रूप से जटिल हैं (Mathematical descriptions are frighteningly complex):
- बात यह है कि इस प्रकार का गणितीय विवरण इतनी भयावह रूप से जटिल होगा कि जब तक आप अपनी गणना में रियायतें देने और इसे एक अनुमान लगाने के लिए तैयार नहीं होते। आप उस गणना को करने के लिए पृथ्वी पर कंप्यूटर को पर्याप्त शक्तिशाली नहीं पाएंगे। मौलिक कणों के बीच बहुत सारी परतें होती हैं जो आपके शरीर और बाइक और उन परस्पर क्रियाओं को बनाती हैं जिनके ऊपर की सभी परतें हैं।
- उदाहरण के लिए, मौलिक कण परमाणु अणु बनाते हैं जो कोशिकाओं को बनाते हैं जो अंगों को बनाते हैं जो आपको बनाते हैं और एक प्रणाली जो बाइक के साथ बातचीत कर रही है और आप डाल रहे हैं। यह बाइक और यह शक्ति फिर से सभी मूलभूत कणों में वापस चली जाती है। यह केवल एक बहुत ही गणितीय वर्णन है। इसलिए, परिणाम को अनुमानित करना बेहतर है। और, हम परिणाम का अनुमान कैसे लगा सकते हैं? वेग के लिए समीकरण का उपयोग करना जो हमने अभी ऊपर देखा था।
- अब, यदि आप मानते हैं कि ब्रह्मांड ब्रह्मांड की शुरुआत से सभी क्रियाओं के रूप में निर्धारक है, तो यह पहले से ही निर्धारित किया गया है और हम कारण और प्रभाव के कारण नहीं बदल सकते हैं। यदि यह पता चला कि ब्रह्मांड और भी निर्धारक है, तो विचार प्रक्रिया भी सामने आई है, वेग के समीकरण को भी गणितीय रूप से वर्णित किया जा सकता है।
- दिन के अंत में, वेग समीकरण एक व्यक्ति के मस्तिष्क में हुई कुछ चीजों का परिणाम है जो कई हिस्सों से बना होता है जो न्यूरॉन्स से बने होते हैं। उन न्यूरॉन्स में एक दूसरे के बीच संबंध होते हैं और एक ऐसे तरीके से बातचीत करते हैं जो वेग के समीकरण का वर्णन कर सकते हैं। यदि आप मूलभूत कणों के बीच की परतों को समझ सकते हैं जो एक मस्तिष्क बनाते हैं जो वेग के साथ आया है.
- उपर्युक्त आर्टिकल में हर चीज का गणितीय सिद्धांत (Mathematical Theory of Everything) के बारे में बताया गया है.
Mathematical Theory of Everything
हर चीज का गणितीय सिद्धांत
(Mathematical Theory of Everything)
Mathematical Theory of Everything
हर चीज का गणितीय सिद्धांत (Mathematical Theory of Everything) का तात्पर्य है कि इस संसार में परमात्मा के अलावा सब अपूर्ण हैं।
पूर्ण ब्रह्म है।सृष्टि,विकास तथा अन्य अनेक परिवर्तनों के बावजूद परमात्मा की पूर्णता अखण्डित है अर्थात् कभी नष्ट नहीं होती है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here |