Formula of Radius of Curvature
1.वक्रता त्रिज्या का सूत्र (Formula of Radius of Curvature),वक्रता त्रिज्या के लिए सूत्र (Formula for Radius of Curvature):
त्रिज्या का सूत्र (Formula of Radius of Curvature):माना LM एक दिया हुआ वक्र है तथा इस पर एक बिन्दु P है,साथ ही वक्र पर Q एक अन्य बिन्दु है।अब P तथा Q पर अभिलम्ब खींचे।माना यह दोनों अभिलम्ब बिन्दु N पर मिलते हैं।अब बिन्दु Q को बिन्दु P की ओर वक्र पर प्रवृत्त (approach) करते हैं।जैसे-जैसे बिन्दु Q,बिन्दु P के समीप पहुंचेगा।वैसे-वैसे बिन्दु N एक निश्चित बिन्दु C पर प्रवृत्त होगा।अतः सीमा में बिन्दु N बिन्दु C पर प्रवृत्त होता है।यहां हमने Q बिन्दु वक्र पर लिया है तथा इस पर कोई प्रतिबन्ध नहीं लगाया है कि वह P के दांए है या बाएं।ऐसी स्थिति में बिन्दु C को बिन्दु P पर वक्र का वक्रता केन्द्र (Centre of Curvature) कहते हैं तथा दूरी CP को बिन्दु P पर वक्रता-त्रिज्या (Radius of Curvature) कहते हैं।CP दूरी के व्युत्क्रम (reciprocal),\frac{1}{CP} को बिन्दु P वक्र की वक्रता (Curvature) कहते हैं।आमतौर पर वक्रता-त्रिज्या को ग्रीक अक्षर (Greek Letter) से निरूपित करते हैं।वह वृत्त जिसका केन्द्र C हो तथा वक्रता त्रिज्या CP हो तो बिन्दु P पर वक्र का वक्रता-वृत्त (Circle of Curvature) कहते हैं तथा बिन्दु P से खींची गई वक्रता-वृत्त में कोई जीवा को वक्रता-जीवा (Chord of Curvature) कहते हैं। \rho=\frac{ds}{d \psi}
(1.)वक्रता-त्रिज्या के लिए कार्तीय सूत्र (Cartesian Formula for Radius of Curvature):
\rho=\frac{\left(1+y_{1}^{2}\right)^{\frac{3}{2}}}{y_{2}}
(2.)प्राचलिक सूत्रों की वक्रता-त्रिज्या (Radius of Curvature for Parametric Curves):
\rho=\frac{\left(x^{\prime^{2}}+y^{\prime^{2}}\right)^{\frac{3}{2}}}{x^{\prime} y^{\prime \prime}-y^{\prime} x^{\prime \prime}} \\ \frac{d x}{d t}=f^{\prime}(t)=x^{\prime}, \frac{d y}{d t}=\phi^{\prime}(t)=y^{\prime}
(3.)वृत्त की वक्रता (Curvature of a Circle):
\frac{1}{\rho}=\frac{d \psi}{d s}
(4)ध्रुवीय रूप में वक्रता त्रिज्या का सूत्र (formula of radius of curvature in polar form):
\rho=\frac{\left[r^{2}+\left(\frac{d r}{d \theta}\right)^{2}\right]^{\frac{3}{2}}}{r^{2}+2\left(\frac{d r}{d \theta}\right)^{2}-r \frac{d^{2} r}{d \theta^{2}}}
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Angle Between Radius Vector and Tangent
2.वक्रता त्रिज्या का सूत्र के उदाहरण (Formula of Radius of Curvature Examples):
निम्न वक्रों के बिन्दु पर वक्रता-त्रिज्या ज्ञात कीजिए:
(Find the radius of curvature of the point on the following curves):
Example:1.s=c \tan \psi
Solution:s=c \tan \psi \\ \frac{d s}{d \psi}=c \sec ^{2} \psi \\ \rho =\frac{d s}{d \psi} \\ \Rightarrow \rho =c \sec ^{2} \psi
Example:2.s=4 a \sin \psi
Solution:s=4 a \sin \psi \\ \frac{d s}{d \psi}=4 a \cos \psi \\ \rho =\frac{d s}{d \psi} \\ \Rightarrow \rho =4 a \cos \psi
Example:3.s=a \log \cot \left(\frac{\pi}{4}-\frac{\psi}{2}\right)
Solution:s=a \log \cot \left(\frac{\pi}{4}-\frac{\psi}{2}\right) \\ \frac{d s}{d \psi} =\frac{a}{\cot \left(\frac{\pi}{4}-\frac{\psi}{2}\right)}\left[-\operatorname{cosec}^{2}\left(\frac{\pi}{4}-\frac{\psi}{2}\right)\right]\left(-\frac{1}{2}\right) \\ =\frac{a \operatorname{cosec}^{2}\left(\frac{\pi}{4} -\frac{\psi}{2}\right)}{2 \cot \left(\frac{\pi}{4}-\frac{\psi}{2}\right)} \\ =\frac{a}{2 \sin \left(\frac{\pi}{4}-\frac{\psi}{2}\right) \cos \left(\frac{\pi}{4}-\frac{\psi}{2}\right)} \\ =\frac{a}{\sin \left(\frac{\pi}{2}-\psi\right)} \\ =\frac{a}{\cos \psi} \\ \Rightarrow \frac{d s}{d \psi}=a \sec \psi \\ \rho=\frac{d s}{d \psi} \\ \Rightarrow \rho =a \sec \psi
Example:4.s=c \log (\sec \psi)
Solution:s=c \log (\sec \psi) \\ \frac{d s}{d \psi}=\frac{c}{\sec \psi} \cdot \sec \psi \tan \psi \\ \Rightarrow \frac{d s}{d \psi}=c \tan \psi \\ \rho =\frac{d s}{d \psi} \\ \Rightarrow \rho =c \tan \psi
Example:5.कार्डिआइड s=4 a \sin \frac{1}{3}(\psi-\frac{\pi}{2}) के किसी बिन्दु पर यदि वक्रता-त्रिज्या तथा शीर्ष और बिन्दु के बीच चाप की लम्बाई s हो तो सिद्ध कीजिए कि
s^{2}+9 \rho^{2}=16 a^{2}
(For the cardiod s=4 a \sin \frac{1}{3}(\psi-\frac{\pi}{2});show that [katex]s^{2}+9 \rho^{2}=16 a^{2} where is the radius of curvature between the vertex and the point.)
Solution:s=4 a \sin \frac{1}{3}(\psi-\frac{\pi}{2}) \\ \frac{d s}{d \psi}=4 a \cos \frac{1}{3}\left(\psi-\frac{\pi}{2}\right) \left[\sin \frac{1}{3}\left(\psi-\frac{\pi}{2}\right)\right] \frac{1}{3} \\ =\frac{4a}{3} \sin \frac{1}{3}\left(\psi-\frac{\pi}{2}\right) \\ =-\frac{4 a}{3}\left[2 \cos \frac{1}{3}(\psi -\frac{\pi}{2})\right] \\ \frac{d s}{d \psi}=-\frac{4a}{3} \cos \frac{1}{3}\left(\psi-\frac{\pi}{2}\right) \\ \rho =\frac{d s}{d \psi} \\ \Rightarrow \rho =-\frac{4 a}{3} \cos \frac{1}{3}\left(\psi-\frac{\pi}{2}\right) \\ s^{2}+9 \rho^{2} =\left[4 a \sin \frac{1}{3}\left(\psi-\frac{\pi}{2}\right)\right]^{2}+9\left[-\frac{4a}{3} \cos \frac{1}{3}\left(\psi-\frac{\pi}{2}\right)\right]^{2} \\ =16 a^{2} \sin ^{2} \frac{1}{3}\left(\psi-\frac{\pi}{2}\right)+16 a^{2} \cos ^{2} \frac{1}{3}\left(\psi-\frac{\pi}{2}\right) \\ =16 a^{2}\left[\sin ^{2} \frac{1}{3}\left(\psi-\frac{\pi}{2}\right)+\cos ^{2} \frac{1}{3}(\psi-\frac{\pi}{2})\right] \\ \Rightarrow s^{2}+9 \rho^{2}=16 a^{2}
Example:6.वक्र s=m\left(\sec ^{3} \psi-1\right) के लिए सिद्ध कीजिए कि
\rho=3 m \tan \psi \sec ^{3} \phi
और.उपर्युक्त की सहायता से सिद्ध कीजिए कि
3 m\left(\frac{d y}{d x}\right)\left(\frac{d^{2} y}{d x^{2}}\right)=1
साथ ही यह भी सिद्ध कीजिए कि यह अवकल समीकरण अर्धधन परवलय द्वारा सन्तुष्ट हो जाती है।
(For the curve s=m\left(\sec ^{3} \psi-1\right); prove that
\rho=3 m \tan \psi \sec ^{3} \phi
and hence show that 3 m\left(\frac{d y}{d x}\right)\left(\frac{d^{2} y}{d x^{2}}\right)=1
Also show that this differential equation is satisfied by the semicubical parabola):
Solution: s=m\left(\sec ^{3} \psi-1\right) \\ \Rightarrow \frac{d c}{d \psi}=m \cdot 3 \sec ^{3} \psi \tan \psi \\ \Rightarrow \frac{d s}{d \psi}=3 m \sec ^{3} \psi \tan \psi \\ 27 m y^{2}=8 x^{3}
x के सापेक्ष अवकलन करने पर:
54 m y\left(\frac{d y}{d x}\right)=24 x^{2} \\ \Rightarrow \left(\frac{d y}{d x}\right)=\frac{24 x^{2}}{54 m y} \\ \Rightarrow \left(\frac{d y}{d x}\right)=\frac{4 x^{2}}{9 m y}
पुनः x के सापेक्ष अवकलन करने पर:
\frac{d^{2} y}{d x^{2}}=\frac{4}{9 m}\left[\frac{y \cdot 2 x-x^{2} \frac{d y}{dx}}{y^{2}}\right] \\ \frac{d^{2} y}{d x^{2}} =\frac{4}{9 m}\left[\frac{2 x y-x^{2} \cdot \frac{4 x^{2}}{9 m y}}{y^{2}}\right] \\ =\frac{4}{9 m}\left[\frac{18 m x y^{2}-4 x^{4}}{9 m y^{3}}\right] \\ =\frac{4}{9 m}\left[\frac{18 mx \cdot \frac{8 x^{3}}{27 m}-4 x^{4}}{9 m y^{3}}\right] \left[ \because y^{2}=\frac{8 x^{3}}{27 m}\right] \\ =\frac{4}{9 m}\left[\frac{16 x^{4}-12 x^{4}}{27 m y^{3}}\right] \\ \Rightarrow \frac{d^{2} y}{d x^{2}}=\frac{16 x^{4}}{243 m^{2} y^{3}} \\ 3 m\left(\frac{4 x^{2}}{9 m y}\right)\left(\frac{16 x^{4}}{243 m^{2} y^{3}}\right) \\ 3 m\left(\frac{d y}{d x}\right)\left(\frac{d^{2} y}{d x^{2}}\right)= 3 m\left(\frac{4 x^{2}}{9 m y}\right)\left(\frac{16 x^{4}}{243 m^{2} y^{3}}\right) \\ =\frac{64 x^{6}}{729 m^{2} y^{4}} \\ =\frac{64 x^{6}}{729 m^{2}\left(\frac{8 x^{3}}{27 m}\right)^{2}}\left[27 m y^{2}=8 x^{3}\right] \\ =\frac{64 x^{6}}{729 m^{2} \cdot \left(\frac{64 x^{6}}{729 m^{2}}\right)} \\ \Rightarrow 3 m\left(\frac{d y}{d x}\right)\left(\frac{d^{2} y}{d x^{2}}\right) =1 \\ \Rightarrow 3 m\left(\frac{d y}{d x}\right)\left(\frac{d^{2} y}{d x^{2}}\right)=1
निम्न वक्रों के किसी बिन्दु 't' पर वक्रता-त्रिज्या ज्ञात कीजिए:
(Find the radius of curvature at any point 't' of the following curves):
Example:7.x=a \cos t, y =b \sin t
Solution: x=a \cos t, y =b \sin t \\ x^{\prime}=\frac{d x}{d t}=-a \sin t , \quad y^{\prime}= \frac{d y}{d t}=b \cos t \\ x^{\prime \prime}=\frac{d^{2} x}{d t^{2}}=-a \cos t, \quad y^{\prime \prime}=\frac{d^{2} y}{d t^{2}}=-b \sin t
वक्रता त्रिज्या का सूत्र: \rho=\frac{\left(x^{\prime ^{2}}+y^{\prime ^{2}}\right)^{\frac{3}{2}}}{x^{\prime} y^{\prime \prime}-y^{\prime} x^{\prime \prime}} \\ =\frac{\left(a^{2} \sin ^{2} t+b^{2} \cos ^{2} t\right)^{\frac{3}{2}}}{(-a \sin t)(-b \sin t)-(b \cos t)(-a \cos t)} \\ =\frac{\left(a^{2} \sin ^{2} t+b^{2} \cos ^{2} t\right)^{\frac{3}{2}}}{a b \sin ^{2} t+a b \cos ^{2} t} \\ \Rightarrow \rho =\frac{\left(a^{2} \sin ^{2} t +b^{2} \cos ^{2} t\right)^{\frac{3}{2}}}{a b}
Example:8.x=a t^{2}, y=2 a t
Solution: x=a t^{2}, y=2 a t \\ x^{\prime}=\frac{d x}{d t}=2 a t, \quad y^{\prime}=\frac{d y}{d t}=2 a \\ x^{\prime \prime}=\frac{d^{2} x}{d t^{2}}=2 a, \quad y^{\prime \prime}=\frac{d^{2} y}{d t^{2}}=0
वक्रता त्रिज्या का सूत्र:\rho=\frac{\left(x^{\prime ^{2}}+y^{\prime ^{2}}\right)^{\frac{3}{2}}}{x^{\prime} y^{\prime \prime}-y^{\prime} x^{\prime \prime}} \\ =\frac{\left[(2at)^{2}+(2a)^{2}\right]^{\frac{3}{2}}}{(2a t)(0)-(2 a)(2 a)} \\ =\frac{\left(4 a^{2} t^{2}+4 a^{2}\right)^{\frac{3}{2}}}{-4 a^{2}} \\ =\frac{8 a^{3}\left(1+t^{2}\right)^{\frac{3}{2}}}{4 a^{2}}
\Rightarrow \rho=2 a\left(1+t^{2}\right)^{\frac{3}{2}}
उपर्युक्त उदाहरणों के द्वारा वक्रता त्रिज्या का सूत्र (Formula of Radius of Curvature),वक्रता त्रिज्या के लिए सूत्र (Formula for Radius of Curvature) को समझ सकते हैं।
3.वक्रता त्रिज्या का सूत्र की समस्याएं (Formula of Radius of Curvature Problems):
(1.)वक्र s=a \log (\sec \psi+\tan \psi) के बिन्दु (s,\psi ) पर वक्रता त्रिज्या ज्ञात कीजिए।
(Find the radius of curvature at the point (s,\psi ) on the curve s=a \log (\sec \psi+\tan \psi).):
(2.) वक्र y=a \cosh (\frac{x}{a}) के लिए सिद्ध कीजिए कि \rho=\frac{y^{2}}{a}
(For the curve y=a \cosh (\frac{x}{a}),prove that \rho=\frac{y^{2}}{a})
(3.)सिद्ध कीजिए कि उस वक्र के लिए जिसमें s=c e^{\frac{x}{c}}, c \rho=s \sqrt{\left(s^{2}-c^{2}\right)}
(Show that for the curve. s=c e^{\frac{x}{c}}, c \rho=s \sqrt{\left(s^{2}-c^{2}\right)} )
उत्तर (Answers):(1) s=a \sec \psi
उपर्युक्त सवालों को हल करने पर वक्रता त्रिज्या का सूत्र (Formula of Radius of Curvature),वक्रता त्रिज्या के लिए सूत्र (Formula for Radius of Curvature)को ठीक से समझ सकते हैं।
Also Read This Article:-Total Differential Formula
4.वक्रता त्रिज्या का सूत्र (Formula of Radius of Curvature) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.वक्रता सूत्र क्या है? (What is curvature formula?):
उत्तर:एक बिंदु M(x,y) पर एक वक्र की वक्रता त्रिज्या को इस बिंदु पर वक्र के वक्रता K का व्युत्क्रम कहा जाता है: R=\frac{1}{K}।इसलिए स्पष्ट समीकरण y=f(x) द्वारा दिए गए समतल वक्रों के लिए,एक बिंदु M(x,y) पर वक्रता की त्रिज्या निम्नलिखित अभिव्यक्ति द्वारा दी जाती है: R=\frac{[1+(y'(x))^{2}]^{\frac{3}{2}}}{y′′(x)}
वक्रता त्रिज्या के कई सूत्र हैं।उपर्युक्त सूत्र वक्रता त्रिज्या के लिए कार्तीय निर्देशांक में वक्रता त्रिज्या की औपचारिक परिभाषा है।
जबकि वक्रता मापता है कि किसी बिंदु पर वक्र कितनी तेजी से दिशा बदल रहा है।वक्र के लिए वक्रता निर्धारित करने के लिए कई सूत्र हैं।
प्रश्न:2.भौतिकी में वक्रता त्रिज्या क्या है? (What is the radius of curvature in physics?):
उत्तर:लेंस के घुमावदार भाग से बने वृत्त की त्रिज्या को वक्रता त्रिज्या के रूप में जाना जाता है।हम लेंस के घुमावदार हिस्से की मदद से एक वृत्त खींचते हैं और इसके केंद्र का पता लगाते हैं,केंद्र से वृत्त की त्रिज्या को मापकर हमें वक्रता की त्रिज्या मिलती है।
प्रश्नः3.वृत्त की वक्रता त्रिज्या कितनी होती है? (What is the radius of curvature of a circle?):
उत्तर:अवकलन ज्यामिति में,वक्रता त्रिज्या (R),वक्रता का व्युत्क्रम है।एक वक्र के लिए,यह वृत्ताकार चाप की त्रिज्या के बराबर होता है जो उस बिंदु पर वक्र का सबसे अच्छा अनुमान लगाता है।सतहों के लिए, वक्रता की त्रिज्या एक वृत्त की त्रिज्या होती है जो किसी सामान्य खंड (Normal Section) या उसके संयोजनों (Combinations) के लिए सबसे उपयुक्त होती है।
प्रश्नः4.ध्रुवीय रूप में वक्रता त्रिज्या का सूत्र क्या है? (What is the formula of radius of curvature in polar form?):
उत्तर:मान लीजिए r=f(θ) ध्रुवीय रूप में वक्र के समीकरण हैं और p(r) इस पर एक बिंदु है।तब इस ध्रुवीय वक्र के लिए वक्रता त्रिज्या का सूत्र निम्नलिखित है:
\rho=\frac{\left[r^{2}+\left(\frac{d r}{d \theta}\right)^{2}\right]^{\frac{3}{2}}}{r^{2}+2\left(\frac{d r}{d \theta}\right)^{2}-r \frac{d^{2} r}{d \theta^{2}}}
प्रश्न:5.आप वक्रता की गणना कैसे करते हैं? (How do you calculate curvature?):
चरण 1: अवकल की गणना करें।वक्रता ज्ञात करने के लिए पहला कदम हमारे फ़ंक्शन का अवकलज लेना है।
चरण 2: अवकलज को हल करें।
चरण 3: स्पर्शरेखा अर्थात् प्रथम अवकलज का पुनः अवकलज लें।
चरण 4: इस मान का परिमाण ज्ञात करें।
चरण 5: इस मानों को निम्नलिखित सूत्र में रखें।
\frac{1}{\rho}=\frac{y_{2}}{\left(1+y_{1}^{2}\right)^{\frac{3}{2}}}
प्रश्नः6.आप सामान्य वक्रता की गणना कैसे करते हैं? (How do you calculate normal curvature?):
उत्तरःवक्रता,वक्रता-त्रिज्या की विलोम होती है।(मेउस्नियर प्रमेय (Meusnier theorem) भी देखें)।अभिलम्ब वक्रता (normal curvature) के माध्यम से कोई ड्यूपिन संकेतक (Dupin indicatrix),गाऊसी वक्रता (Gaussian curvature) और सतह की औसत वक्रता (mean curvature) के साथ-साथ सतह की स्थानीय ज्यामिति की कई अन्य अवधारणाओं का निर्माण कर सकता है।
प्रश्न:7.क्या वक्रता त्रिज्या ऋणात्मक हो सकती है? (Can radius of curvature negative?):
उत्तरःयदि शीर्ष (Vertex) वक्रता केंद्र के बाईं ओर स्थित है,तो वक्रता त्रिज्या धनात्मक होती है।यदि शीर्ष वक्रता केंद्र के दाईं ओर स्थित है,तो वक्रता त्रिज्या ऋणात्मक है।
प्रश्नः8.भौतिकी में वक्रता केंद्र क्या है? (What is Centre of curvature in physics?):
उत्तरःज्यामिति में,वक्र का वक्रता केंद्र उस बिंदु पर पाया जाता है जो वक्र से अभिलम्ब वेक्टर पर स्थित वक्रता त्रिज्या के बराबर दूरी पर होता है।यदि वक्रता शून्य है तो यह अनंत का बिंदु है।वक्र से दोलन करने वाला वृत्त वक्रता के केंद्र पर केंद्रित होता है।
प्रश्नः9.अभिलम्ब वक्रता क्या है? (What is normal curvature?):
उत्तरःएक नियमित सतह और उस सतह के भीतर एक वक्र को देखते हुए, एक बिंदु पर अभिलम्ब वक्रता सतह की अभिलाम्बिक दिशा में वक्र की वक्रता की मात्रा है।सतह पर वक्र स्पर्शरेखा,वक्रता और अभिलम्ब के साथ एक बिंदु से होकर गुजरता है।
प्रश्नः10.सांख्यिकी में वक्रता क्या है? (What is curvature in statistics?):
उत्तरःसहज रूप से,वक्रता वह राशि है जिसके द्वारा एक वक्र एक सीधी रेखा से विचलित हो जाता है या एक सतह एक समतल होने से विचलित हो जाती है।वक्रों के लिए,विहित उदाहरण एक वृत्त का होता है,जिसकी वक्रता त्रिज्या के व्युत्क्रम के बराबर होती है।
प्रश्नः11.आप अधिकतम वक्रता कैसे ज्ञात करते हैं? (How do you find the maximum curvature?):
\frac{dT}{ds} =\frac{\frac{dT}{dt } }{\frac{ds}{dt}} =kN, जहाँ k आपकी वक्रता है।इसलिए यदि आप \frac{dT}{ds} की गणना करते हैं और फिर सदिश का परिमाण ज्ञात करते हैं जो t के कार्य के रूप में k, वक्रता देता है।फिर आप मूल कैलकुलस (\frac{dk}{dt}=0) का उपयोग करके देख सकते हैं कि k का अधिकतम कहां है।
प्रश्नः12.आप वक्रता त्रिज्या में कैसे वृद्धि करते हैं?(How do you increase radius of curvature?):
या हम दूसरी तरफ जा सकते हैं,अगर हम वक्रता की मात्रा कम करते हैं, तो हमें वक्रता त्रिज्या की मात्रा में वृद्धि मिलती है।किसी भी घटना में,जब एक कारक चलता है,तो दूसरा कारक विपरीत दिशा में जाता है।तो,लब्बोलुआब यह है कि, लेंस की वक्रता बढ़ने से वक्रता की त्रिज्या कम हो जाएगी।
प्रश्नः13.वक्रता और त्रिज्या का केंद्र क्या है? (What is Centre of curvature and radius?):
वक्रता केंद्र -गोले का वह भाग जिसका दर्पण भाग होता है, दर्पण का वक्रता केंद्र कहलाता है।वक्रता त्रिज्या -जिस गोले का दर्पण भाग होता है उसकी त्रिज्या दर्पण की वक्रता त्रिज्या कहलाती है।
प्रश्नः14.क्या वक्रता त्रिज्या वक्रता केंद्र के बराबर है? (Is radius of curvature equal to Centre of curvature?):
उत्तरःनहीं,वक्रता केंद्र और वक्रता त्रिज्या समान नहीं हैं।
प्रश्नः15.वृत्त की वक्रता क्या होती है? (What is the curvature of a circle?):
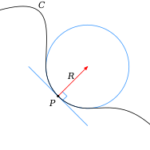
उत्तर:वृत्त के प्रत्येक बिंदु पर वक्रता,वक्रता त्रिज्या का व्युत्क्रम है;अन्य वक्रों के लिए (और सीधी रेखाएँ,जिन्हें अनंत त्रिज्या के वृत्त के रूप में माना जा सकता है),वक्रता वृत्त की त्रिज्या का व्युत्क्रम है जो दिए गए बिंदु पर वक्र के सबसे निकट से मेल खाती है।(चित्र देखें)।
प्रश्नः15.धनात्मक और ऋणात्मक वक्रता क्या है? (What is positive and negative curvature?):
उत्तरःएक सतह में एक बिंदु पर धनात्मक वक्रता होती है, यदि सतह उस बिंदु से उसी दिशा में वक्रित होती है जो सतह पर स्पर्शरेखा के सापेक्ष होती है भले ही काटने वाले समतल की परवाह किए बिना।एक सतह पर एक बिंदु पर ऋणात्मक वक्रता होती है यदि सतह दो अलग-अलग दिशाओं में स्पर्शरेखा तल से दूर हो जाती है।
प्रश्नः16.वक्रता के लिए दूसरा शब्द क्या है? (What is another word for curvature?):
उत्तर:चाप मोड़(arc bend)
घुमावदार कोण(curving angle)
धनुषाकार धनुष (arch bow)
बदमाश वक्रता(crook curvity)
विक्षेपण वंक(deflection flexure)
प्रश्नः16.वक्रता किन स्थितियों में अधिकतम और न्यूनतम मान रखती है? (At what positions does the curvature have maximum and minimum values?):
उत्तरःऊपर दीर्घवृत्त का ग्राफ देखें।वक्रता x=2 और y=0 और x=-2 और y=0 के पास सबसे बड़ी है।ये बिंदु t=0 और t=\pi के अनुरूप हैं।वक्रता के लिए उपरोक्त व्यंजक में, t=0 या t=\pi होने पर भाजक अपने न्यूनतम पर होता है, जिसका अर्थ है कि वक्रता अधिकतम पर है।
प्रश्नः17.वक्रता त्रिज्या और मुख्य अक्ष में क्या अंतर है? (What is difference between radius of curvature and principal axis?):
उत्तरःवक्रता त्रिज्या- गोलीय दर्पण के गोले की त्रिज्या एक भाग है,दर्पण की वक्रता त्रिज्या कहलाती है।प्रिंसिपल एक्सिस- यह दर्पण के ध्रुव को इसके वक्रता केंद्र से मिलाने वाली सीधी रेखा है।
प्रश्नः18.वक्रता कोण क्या है? (What is angle of curvature?):
उत्तरः(जियोम Geom) एक जो वक्र की वक्रता की मात्रा को व्यक्त करता है।यह भी देखें: वक्रता।
प्रश्नः19.धनात्मक वक्रता का क्या अर्थ है? (What does positive curvature mean?):
उत्तरःयदि आपके पास धनात्मक वक्रता वाला त्रिभुज है,तो त्रिभुज के कोणों का योग 180 डिग्री से बड़ा होता है।इसी तरह ऋणात्मक वक्रता का अर्थ है कि कोणों का योग 180 डिग्री से कम है।
प्रश्नः20.आप एक परवलय की वक्रता कैसे ज्ञात करते हैं? (How do you find the curvature of a parabola?):
उत्तर:सामान्य तौर पर, वक्र के एक बिंदु में वक्रता उस बिंदु में "सर्वश्रेष्ठ फिटिंग सर्कल" के त्रिज्या से 1 को विभाजित होती है।
एक परवलय के लिए,इसके शीर्ष में वक्रता अधिकतम (सबसे छोटा वृत्त) होगी और जब आप वक्र के साथ चलते हैं तो धीरे-धीरे कम हो जाती है।
तो एक परवलय के लिए कोई एकल वक्रता मान नहीं है।
प्रश्नः21.वक्रता का क्या अर्थ है? (What does curvature mean?):
उत्तर:1.वक्रता की क्रिया :वक्री होने की अवस्था।2.विशेष रूप से वक्रता की एक माप या मात्रा: कोण के परिवर्तन की दर जिसके माध्यम से वक्र के स्पर्शरेखा वक्र के साथ चलती है और जो एक वृत्त के लिए त्रिज्या के व्युत्क्रम के बराबर है।
प्रश्नः22.परवलय की वक्रता त्रिज्या क्या है? (What is radius of curvature of parabola?):
उत्तर:फिर परवलय की वक्रता त्रिज्या को निम्न सूत्र द्वारा परिभाषित किया जाता है: R=\frac{[1+(y′)^{2}]^{\frac{3}{2}}}{y′′}=\frac{[1+(2x)^{2}]^{\frac{3}{2}}}{2}=\frac{(1+4x^{2})^{\frac{3}{2}}}{2}.मूल बिंदु पर (x=0 पर), वक्रता त्रिज्या और वक्रता क्रमशः हैं। R(x=0)=\frac{(1+4⋅0^{2})^{\frac{3}{2}}}{2}=\frac{1}{2} , \quad K=2.
उपर्युक्त प्रश्नों के उत्तर द्वारा वक्रता त्रिज्या का सूत्र (Formula of Radius of Curvature),वक्रता त्रिज्या के लिए सूत्र (Formula for Radius of Curvature) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा वक्रता त्रिज्या का सूत्र (Formula of Radius of Curvature),वक्रता त्रिज्या के लिए सूत्र (Formula for Radius of Curvature) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |









