Basic Proportionality Theorem Class 10
1.आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem Class 10),थेल्स प्रमेय (Thales Theorem):
आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem Class 10) जिसे थेल्स प्रमेय के नाम से भी जाता है निम्न प्रकार है:
प्रमेय (Theorem):1.यदि किसी त्रिभुज की एक भुजा के समान्तर अन्य दो भुजाओं को भिन्न-भिन्न बिन्दुओं पर प्रतिच्छेद करने के लिए एक रेखा खींची जाए तो ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित होती है।
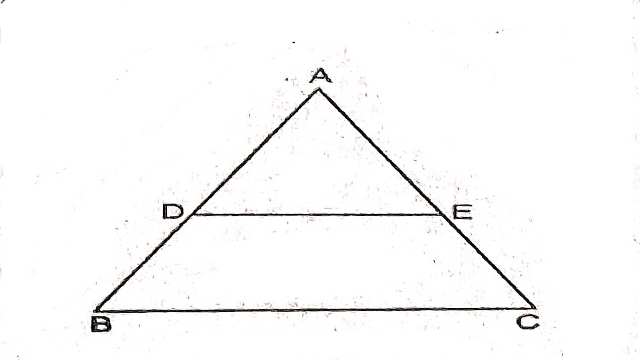
दिया है (Given): \triangle ABC में D E \parallel B C तथा DE अन्य दो भुजाओं AB और AC को क्रमशः D व E पर काटती है।
सिद्ध करना है (To Prove): \frac{A D}{A B}=\frac{A E}{B C}
रचना (Construction):B और E तथा C और D को मिलाया।और फिर DM \perp AC एवं EN \perp A B खींचा।
उपपत्ति (Proof):\triangle ADE का क्षेत्रफल=\frac{1}{2} × आधार ×ऊँचाई
=\frac{1}{2} \times AD \times EN \\ \Rightarrow \operatorname{ar}(ADE)=\frac{1}{2} \times A D \times EN
इसी प्रकार \operatorname{ar}(BDE)=\frac{1}{2} \times DB \times E N \\ \frac{\operatorname{ar}(ADE)}{\operatorname{ar}(B D E)}=\frac{\frac{1}{2} \times A D \times E N}{\frac{1}{2} \times D B \times E N} \\ \Rightarrow \frac{\operatorname{ar}(ADE)}{\operatorname{ar}(BDE)}=\frac{AD}{DB} \cdots(1)
इसी प्रकार ar (ADE)=\frac{1}{2} \times AE \times D M
तथा ar (D E C)=\frac{1}{2} \times AE \times D M \\ \frac{ar(A D E)}{a_{r}(D E C)}=\frac{\frac{1}{2} \times A E \times D M}{\frac{1}{2} \times E C \times D M} \\ \frac{ar(A D E)}{ar(D E C)}=\frac{A E}{E C} \cdots(2)
\triangle BDE और \triangle DEC एक ही आधार DE तथा समान्तर रेखाओं BC और DE के बीच बने दो त्रिभुज हैं।
अत: ar(BDE)=ar(DEC)…. (3)
इसलिए (1),(2),(3) से:
\frac{A D}{D B}=\frac{A E}{E C}
प्रमेय (Theorem):2.आधारभूत आनुपातिकता प्रमेय का विलोम (Converse of Basic Proportionality Theorem):
यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करे तो वह तीसरी भुजा के समान्तर होती है।
दिया है (Given):\triangle ABC में भुजा AB व AC को इस प्रकार प्रतिच्छेदित करती है कि
\frac{A D}{D B}=\frac{A E}{E C}
सिद्ध करना है (To Prove):D E \| B C
रचना (Construction):यदि DE भुजा BC के समान्तर न हो तो B C \| P E^{\prime} खींची।
उपपत्ति (Proof):B C \| P E^{\prime}(रचना से)
\frac{A D}{D B}=\frac{A E^{\prime}}{E^{\prime} C} (आधारभूत आनुपातिकता प्रमेय से)….(1)
\frac{A D}{D B}=\frac{A E}{E C}(दिया है)….(2)
(1) व (2) से:
\frac{A E^{\prime}}{E^{\prime} C}=\frac{A E}{E C} \\ \Rightarrow \frac{A E^{\prime}}{E^{\prime} C}+ 1=\frac{A E}{EC}+1 \\ \Rightarrow \frac{A E^{\prime}+E^{\prime} C}{E^{\prime} C}=\frac{A E+E C}{E C} \\ \Rightarrow \frac{AC}{E^{\prime} C}=\frac{A C}{E C} \\ \Rightarrow E^{\prime} C=E C
यह तभी संभव है जब E’, E के संपाती हो। अर्थात् DE’, DE के संपाती हो। फलतः D E \| B C
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Nature of Roots of Quadratic Equations
2.आधारभूत आनुपातिकता प्रमेय के उदाहरण (Basic Proportionality Theorem Class 10 Examples):
Example:1.आकृति (i) और (ii) में DE\|BC है।(i) में EC और (ii) में AD ज्ञात कीजिए:
Solution:(i)DE\|BC \\ \frac{A D}{B D}=\frac{A E}{E C} (BPT से)
\frac{1.5}{3}=\frac{1}{E C} \\ E C=\frac{1}{0.5} \\ E C=2 cm
Solution:(ii)DE\|BC \\ \frac{A D}{B D}=\frac{A E}{E C} (BPT से)
\frac{A D}{7.2}=\frac{1.8}{5.4} \\ \Rightarrow A D=\frac{1.8}{5.4} \times 7.2 \\ \Rightarrow A D=2.4 cm
Example:2.किसी \triangle PQR की भुजाओं PQ और PR पर क्रमशः बिन्दु E और F स्थित हैं। निम्नलिखित में से प्रत्येक स्थिति के लिए बताइए कि क्या EF \parallel QR है:
(i)PE=3.9cm,EQ=3cm,PF=3.6cm और FR=2.4cm
Solution: \frac{P E}{E Q}=\frac{3.9}{3}=1.3 \\ \frac{P F}{F R}=\frac{3.6}{2.4}=\frac{3}{2} \\ \Rightarrow \frac{P E}{E Q} \neq \frac{P F}{F R}
अत: EF \not \parallel QR
(ii)PE=4cm,QE=4.5cm,PF=8cm और RF=9cm
\frac{P E}{Q E}=\frac{4}{4.5}=\frac{5}{9} \\ \frac{P F}{R F}=\frac{8}{9} \\ \frac{P E}{Q E} \neq \frac{P F}{R F}
अत: EF \not \parallel QR
(iii)PQ=1.28cm,PR=2.56cm,PE=0.18cm और PF=0.36cm
\frac{P Q}{P E}=\frac{1.28}{0.18}=\frac{64}{9} \\ \frac{P R}{P F}=\frac{2.56}{0.36}=\frac{64}{9} \\ \frac{P Q}{P E}=\frac{P R}{P F}
अत: EF \parallel QR
Example:3.आकृति में यदि L N \| C B और L N \| C D हो तो सिद्ध कीजिए कि \frac{A M}{A B}=\frac{A N}{A D} है।
दिया है (Given):L M \| C B और LN \| C D
सिद्ध करना है (To Prove): \frac{A M}{A B}=\frac{A N}{A D}
उपपत्ति (Proof):\triangle ABC में L M \| C B
अत: \frac{A M}{A B}=\frac{A L}{A C} (BPT से)
इसी प्रकार \triangle ADC में L N \| C D
\frac{A N}{A D}=\frac{A L}{A C} (BPT से)…..(2)
\frac{A N}{A D}=\frac{A M}{A B} Q.E.D.
Example:4.आकृति में DE \| AC और DF \| AE है।सिद्ध कीजिए कि \frac{B F}{F E}=\frac{B E}{E C} है।
दिया है (Given): DE \| AC और DF \| AE
सिद्ध करना है (To Prove): \frac{B F}{F E}=\frac{B E}{E C}
उपपत्ति (Proof):\triangle BAE में DF \| AE
\frac{B F}{F E}=\frac{B D}{D A} (आधारभूत आनुपातिकता प्रमेय से)
\triangle BAC में D E \| A C
\frac{B E}{E C}=\frac{B D}{D A} (आधारभूत आनुपातिकता प्रमेय से)
\frac{B F}{F E}=\frac{B E}{E C} Q.E.D.
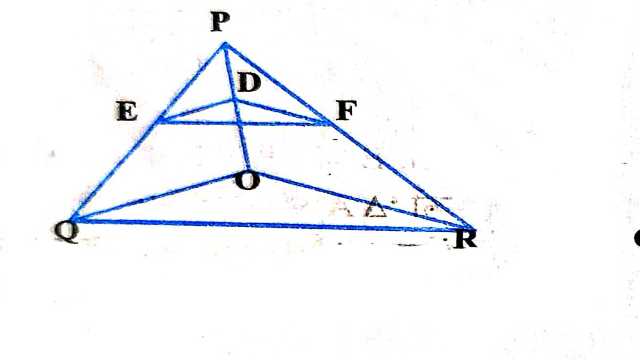
Example:5.आकृति में DE \parallel OQ और DF \parallel OR है।दर्शाइए कि EF \parallel QR है।
दिया है (Given):DE \parallel OQ और DF \parallel OR
सिद्ध करना है (To Prove): EF\|QR
उपपत्ति (Proof): \triangle POQ में DE \|OQ
\frac{P E}{EQ}=\frac{P D}{D O} (आधारभूत आनुपातिकता प्रमेय से) …(1)
\triangle POR में DF \| OR
\frac{P F}{FR}=\frac{P D}{D O} (आधारभूत आनुपातिकता प्रमेय से)
(1) व (2) से:
\frac{P E}{E Q}=\frac{P F}{F R}
अब \triangle POR में
\frac{P E}{E Q}=\frac{P F}{F R} (सिद्ध किया है)
E F \| Q R (आधारभूत आनुपातिकता प्रमेय के विलोम से)
Example:6.आकृति में क्रमशः OP, OQ और OR पर स्थित बिन्दु A,B और C इस प्रकार हैं कि A B \| P Q और A C \| P R है। दर्शाइए कि BC \| Q R है।
दिया है (Given):A B \| P Q और A C \| P R
सिद्ध करना है (To Prove): BC \| Q R
उपपत्ति (Proof):\triangle POQ में A B \| P Q \\ \frac{A O}{P A}=\frac{B O}{B Q} (आधारभूत आनुपातिकता प्रमेय से)
(1) व (2) से:
\triangle POR में A C \| P R \\ \frac{AO}{P A}=\frac{O C}{C R} (सिद्ध किया है)….(2)
\frac{B O}{B Q}=\frac{O C}{C R} (आधारभूत आनुपातिकता प्रमेय से)
\triangle QOR में
\frac{B O}{B Q}=\frac{O C}{C R} (सिद्ध किया है)
BC \parallel QR (आधारभूत आनुपातिकता प्रमेय से)
Example:7.आधारभूत आनुपातिकता प्रमेय का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य-बिन्दु से होकर दूसरी भुजा के समान्तर खींची गई रेखा तीसरी को समद्विभाजित करती है।
दिया है (Given):\triangle ABC में D, AB का मध्य-बिन्दु है अर्थात् AD=DB तथा DE \| BC
सिद्ध करना है (To Prove):AE=EC
उपपत्ति (Proof):AD=DB (दिया है)
\Rightarrow \frac{A D}{D B}=1 \cdots(1)
\triangle ABC में DE \| BC
\frac{A D}{D B}=\frac{A E}{E C} (आधारभूत आनुपातिकता प्रमेय से)
(1) व (2) से:
1=\frac{A E}{E C} \\ \Rightarrow A E=E C
Example:8.आधारभूत आनुपातिकता प्रमेय के विलोम का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं के मध्य बिन्दुओं को मिलनेवाली रेखा तीसरी भुजा के समान्तर होती है।
दिया है (Given):\triangle ABC में AB व AC के मध्य बिन्दुओं क्रमशः D और E हैं अर्थात् AD=DB और AE=EC है।
सिद्ध करना है (To Prove): DE \| BC
उपपत्ति (To Proof):AD=DB (दिया है)
\Rightarrow \frac{A D}{D B}=1 \cdots(1)
AE=EC (दिया है)
\frac{A E}{E C}=1 \cdots(2)
(1) व (2) से:
\frac{A D}{D B}=\frac{A E}{E C}
अत: D E \| B C (आधारभूत आनुपातिकता प्रमेय के विलोम से)
Example:9.ABCD एक समलम्ब है जिसमें AB \| DC है तथा इसके विकर्ण परस्पर O बिन्दु पर प्रतिच्छेद करते हैं। दर्शाइए कि \frac{A O}{BO}=\frac{C O}{D O} है।
दिया है (Given):ABCD एक समलम्ब चतुर्भुज है अर्थात् AB \| CD तथा इसके विकर्ण DB व AC एक-दूसरे को O पर प्रतिच्छेद करते हैं।
सिद्ध करना है (To Prove): \frac{A O}{BO}=\frac{C O}{D O}
रचना (Construction):O से OE \| DC खींची।
उपपत्ति (Proof): \triangle ADC में OE \| DC
\frac{A O}{CO}=\frac{A E}{E D} (आधारभूत आनुपातिकता प्रमेय से)…..(1)
परन्तु समलम्ब चतुर्भुज में CD \| AB \\ OE \| CD (रचना से)
अत: O E \| A B
\triangle ADB में O E \| A B
\frac{E D}{A E}=\frac{D O}{BO} (आधारभूत आनुपातिकता प्रमेय से)
\frac{B O}{D O}=\frac{A E}{ED} \cdots(2)
(1) व (2) से:
\frac{B O}{D O}=\frac{A O}{CO} \Rightarrow \frac{A O}{B O}=\frac{C O}{D O}
Example:10.एक चतुर्भुज ABCD के विकर्ण परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते हैं कि \frac{A O}{B O} =\frac{C O}{D O} है। दर्शाइए कि ABCD समलम्ब चतुर्भुज है।
दिया है (Given):ABCD समलम्ब चतुर्भुज के विकर्ण BD व AC एक-दूसरे को इस प्रकार प्रतिच्छेद करते हैं कि \frac{A O}{B O} =\frac{C O}{D O}
सिद्ध करना है (To Prove):ABCD एक समलम्ब चतुर्भुज है अर्थात् AB \parallel CD
रचना (Construction):O से OE \parallel DC खींची।
उपपत्ति (Proof):\triangle BDC में OE \parallel DC \\ \frac{B O}{D O}=\frac{B E}{E C} (आधारभूत आनुपातिकता प्रमेय से)
\frac{A O}{B O}=\frac{CO}{DO}(दिया है)
\Rightarrow \frac{B O}{D O}=\frac{A O}{B O} \cdots(2)
(1) व (2) से: \frac{A O}{C O}=\frac{B E}{E C} \\ O E \parallel AB (आधारभूत आनुपातिकता प्रमेय से)
O E \parallel D C (रचना से)…..(4)
(3) व (4) से:
A B \parallel CD
अत: ABCD समलम्ब चतुर्भुज है।
Example:11.कोष्ठकों में दिए शब्दों में से सही शब्दों का प्रयोग करते हुए रिक्त स्थानों को भरिए:
(i)सभी वृत्त…. होते हैं। (सर्वांगसम/समरूप)
उत्तर:समरूप
(ii)सभी वर्ग… होते हैं। (समरूप,सर्वांगसम)
उत्तर:समरूप
(iii) सभी…. त्रिभुज समरूप होते हैं। (समद्वबाहु, समबाहु)
उत्तर:समबाहु
(iv) भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं यदि (i) उनके संगत कोण…. हों। (ii) उनकी संगत भुजाएँ…. हों। (बराबर, समानुपाती)
उत्तर (i) बराबर (ii) समानुपाती
Example:12.निम्नलिखित युग्मों के दो भिन्न-भिन्न उदाहरण दीजिए:
(i) समरूप
उत्तर:ताजमहल का स्मारक तथा ताजमहल का माॅडल
एक ही नेगेटिव फोटो की स्टैंप साइज फोटो, पासपोर्ट साइज फोटो, पोस्टकार्ड साइज फोटो
(ii) ऐसी आकृतियाँ जो समरूप नहीं है।
उत्तर:एक त्रिभुज और एक वर्ग समरूप नहीं है।
एक चतुर्भुज और पंचभुज समरूप नहीं है।
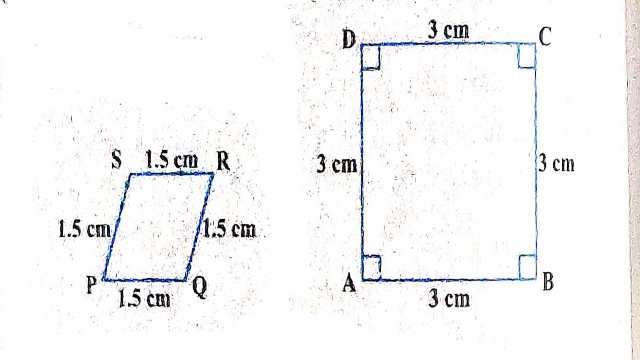
Example:13.बताइए कि निम्नलिखित चतुर्भुज समरूप हैं या नहीं :
उत्तर:\frac{P Q}{A B}=\frac{Q R}{B C}=\frac{P S}{C D}=\frac{S P}{D A}=\frac{1.5}{3} =\frac{1}{2}
परन्तु \angle P \neq \angle A ,\angle Q \neq \angle B, \angle R \neq \angle C ,\angle S \neq \angle D
अत:चतुर्भुज समरूप नहीं है।
उपर्युक्त उदाहरणों के द्वारा आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem Class 10),थेल्स प्रमेय (Thales Theorem) को समझ सकते हैं।
3.आधारभूत आनुपातिकता प्रमेय की समस्याएँ (Basic Proportionality Theorem Class 10 Problems):
(1.)आकृति में यदि DE \parallel BC हो तो x का मान होगा:
(2.)दी गई आकृति \triangle ABCमें DE \parallel BC तथा AD=(7x-4)सेमी,AE=(5x-2)सेमी,DB=(3x+4)सेमी,BC=3xसेमी हो तो x का मान होगा:
उत्तर (Answers):(1)x=\sqrt{7}
(2.) 4 मीटर
उपर्युक्त सवालों को हल करने पर आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem Class 10),थेल्स प्रमेय (Thales Theorem) को ठीक से समझ सकते हैं।
Also Read This Article:-Finding Roots by Quadratic Formula
4.आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem Class 10),थेल्स प्रमेय (Thales Theorem) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.थेल्स कौन थे? (Who was Thales?):
उत्तर:दो त्रिभुजों के संगत कोण बराबर हों तो वे समकोणिक त्रिभुज (equiangular triangles) कहलाते हैं ।एक प्रसिद्ध यूनानी गणितज्ञ थेल्स (Thales) ने दो समकोणिक त्रिभुजों से सम्बन्धित एक महत्त्वपूर्ण तथ्य प्रतिपादित किया जो निम्न है:
दो समानकोणिक त्रिभुजों में उनकी संगत भुजाओं का अनुपात सदैव समान रहता है जिसे आधारभूत आनुपातिकता प्रमेय (थेल्स प्रमेय) कहा जाता है।
प्रश्न:2.समरूपता से क्या तात्पर्य है? (What is meant by similarity?):
उत्तर:ऐसी आकृतियाँ जिनका रूप या आकृतियाँ (shape) बिल्कुल समान हो किन्तु आमाप (size) समान होना आवश्यक न हो समरूप आकृतियाँ (similar figure) कहलाती हैं।
प्रश्न:3.सर्वांगसमता से क्या तात्पर्य है? (What is meant by congruent?):
उत्तर:दो त्रिभुज सर्वांगसम कहे जाते हैं जब उनके समान आकार (shape) तथा समान आमाप (size) हों।
प्रश्न:4.दो बहुभुज कब समरूप होते हैं? (When are two polygons similar?):
उत्तर:भुजाओं की समान संख्या वाले बहुभुज समरूप होते हैं यदि उनके संगत कोण बराबर हो तथा इनकी संगत भुजाएँ एक ही अनुपात में हो (अर्थात् समानुपाती हों)
बहुभुजों के लिए संगत भुजाओं के इस एक ही अनुपात को स्केल गुणक (scale factor) [अथवा प्रतिनिधित्व भिन्न (Representative Fraction) कहा जाता है।
इस प्रकार सर्वांगसम आकृतियाँ समरूप होती है परन्तु सभी समरूप आकृतियों का सर्वांगसम होना आवश्यक नहीं है।
उपर्युक्त प्रश्नों के उत्तर द्वारा आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem Class 10),थेल्स प्रमेय (Thales Theorem)के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Basic Proportionality Theorem Class 10
आधारभूत आनुपातिकता प्रमेय
(Basic Proportionality Theorem Class 10)
Basic Proportionality Theorem Class 10
आधारभूत आनुपातिकता प्रमेय (Basic Proportionality Theorem Class 10) जिसे थेल्स प्रमेय
के नाम से भी जाता है निम्न प्रकार है:




















There was many mistakes please do carefully