To Use Method of Contour Integration
1.परिरेखा समाकलन विधि का प्रयोग करना (To Use Method of Contour Integration),परिरेखा समाकलन (Contour Integration):
परिरेखा समाकलन विधि का प्रयोग करना (To Use Method of Contour Integration) के इस आर्टिकल में विभिन्न प्रकार के निश्चित समाकलों के मान निकालने के लिए दन्तुरण सहित या दन्तुरण रहित वृत्ताकार परिरेखाओं का प्रयोग करके सवालों को हल करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Use Method of Contour Integration
2.परिरेखा समाकलन विधि का प्रयोग करना के उदाहरण (To Use Method of Contour Integration Illustrations):
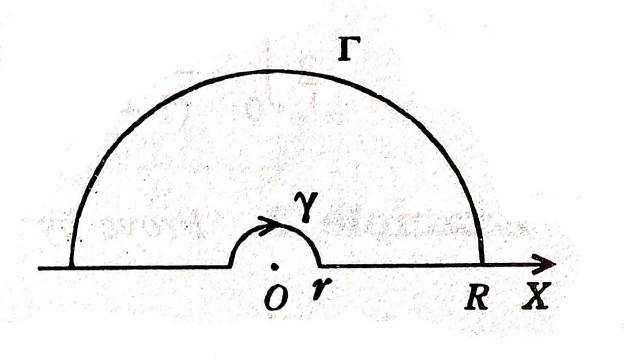
Illustration:1.सिद्ध कीजिए कि \int_0^{\infty} \frac{\log x}{\left(1+x^2\right)^2} d x=-\frac{\pi}{4} मूलबिन्दु पर इंडेन्ट किए गए ऊपरी अर्धतल में एक बड़े अर्धवृत को परिरेखा के रूप में प्रयोग करते हुए।
(Prove that \int_0^{\infty} \frac{\log x}{\left(1+x^2\right)^2} d x=-\frac{\pi}{4} , using as a contour a large semi-circle in the upper half plane indented at the origin.)
Solution: \int_c \frac{\log z}{\left(1+z^2\right)^2} d z=\int_c f(z) dz पर विचार करो,जहाँ C प्रश्न में दी गई परिरेखा है।
z=\pm i , f(z) के द्विक अनन्तक है।केवल z=i,C के अन्दर स्थित है।
z=i पर अवशेष=\phi^{\prime}(i) \\ \phi(z)=\frac{\log z}{(z+i)^2} \\ \log \phi(z)=\log \log (z)-2 \log (z+i)
अवकलन करने परः
\frac{\phi^{\prime}(z)}{\phi(z)} =\frac{1}{z \log z}-\frac{2}{z+i} \\ \Rightarrow \phi^{\prime}(z) =\phi(z)\left[\frac{1}{z \log z}-\frac{2}{z+i}\right] \\ \therefore \phi^{\prime}(i) =\frac{\log i}{-4}\left[\frac{1}{i \log i}-\frac{1}{i}\right] \\ =-\frac{(1-\log i)}{4i} \\ =-\frac{1}{4 i}\left(1-\log e^{\frac{i \pi}{2}}\right) \\ \Rightarrow \phi^{\prime}(i) =-\frac{1}{4 i}\left(1-\frac{i \pi}{2}\right)
अवशेष प्रमेय द्वारा:
\int_c f(z) d z=\int_r^R f(x) d x+\int_{\Gamma} f(z) d z+\int_R^r f\left(x e^{i \pi}\right) e^{i \pi} dx+\int_\gamma f(z) d z=2 \pi i \Sigma R^{+} \cdots(1) \\ \left|\int_{\Gamma} f(z) d z\right| \leq \int_0^\pi \mid \frac{\log \left(R e^{i \theta}\right)}{\left(1+R^2 e^{i 2 \theta}\right)^2} R i e^{i \theta} \mid d \theta \\ \leq \int_0^\pi \frac{\log R+\theta}{\left(R^2-1\right)^2} R d \theta \\ =\frac{\left(\pi \log R+\frac{1}{2} \pi^2\right) R}{\left(R^2-1\right)^2} \\=\frac{R^2}{\left(R^2-1\right)^2}\left(\frac{\pi \log R}{R}+\frac{1}{2} \pi^2 \cdot \frac{1}{R}\right) \rightarrow 0 as R \rightarrow \infty since \underset{R \longrightarrow \infty}{\lim} \frac{\log R}{R}=0
इसी प्रकार \left|\int_r{\gamma} f(z) d z\right| \le \int_0^\pi\left|f\left(r e^{i \theta}\right) r i e^{i \theta} \right| d \theta \rightarrow 0
जबकि \underset{r \longrightarrow 0}{\lim} r \log r=\underset{r \longrightarrow 0}{\lim} \frac{\log r}{\frac{1}{r}}=0
जब r \rightarrow 0, R \rightarrow \infty , (1) से:
\int_0^{\infty} f(x) d x-\int_{\infty}^0 f\left(x e^{i \pi}\right) d x=2 \pi i \Sigma R^{+} \\ \Rightarrow \int_0^{\infty} \frac{\log x}{\left(1+x^2\right)^2} d x+\int_0^{\infty} \frac{\log x e^{i \pi}}{\left(1+x^2 e^{i 2 \pi}\right)^2} dx=2 \pi i \cdot\left[-\frac{1}{4 i}\left(1-\frac{i \pi}{2}\right)\right] \\ =-\frac{\pi}{2} \left(1-\frac{i \pi}{2}\right)
दोनों पक्षों के वास्तविक भागों की तुलना करने पर:
2 \int_0^{\infty} \frac{\log x}{\left(1+x^2\right)^2} d x=-\frac{\pi}{2} \\ \Rightarrow \int_0^{\infty} \frac{\log x}{\left(1+x^2\right)^2} d x=-\frac{\pi}{4}
Illustration:2.परिरेखा समाकलन द्वारा सिद्ध कीजिए \int_0^{\infty} \frac{\log \left(1+x^2\right)}{1+x^2} d x=\pi \log 2 और यह निष्कर्ष निकालिए कि
\int_0^1 \frac{\log \left(x+\frac{1}{x}\right)}{1+x^2} d x=\frac{\pi}{2} \log 2
(Prove by contour integration \int_0^{\infty} \frac{\log \left(1+x^2\right)}{1+x^2} d x=\pi \log 2 and deduce that \int_0^1 \frac{\log \left(x+\frac{1}{x}\right)}{1+x^2} d x=\frac{\pi}{2} \log 2 )
Solution: \int_0^{\infty} \frac{\log \left(1+x^2\right)}{1+x^2} d x=\pi \log 2 \cdots(1) के लिए पाठ्यपुस्तक का उदाहरण देखें।
माना I=\int_0^1 \frac{\log \left(x+\frac{1}{x}\right)}{1+x^2} d x \\ =\int_0^{\infty} \frac{\log \left(x+\frac{1}{x}\right)}{1+x^2} d x+\int_{\infty}^{1} \frac{\log \left(x+\frac{1}{x}\right)}{1+x^2} d x \cdots(2) \\ \int_{\infty}^{1} \frac{\log \left(x+\frac{1}{x}\right)}{1+x^2} dx=-\int_0^1 \frac{\log \left(t+\frac{1}{t}\right)}{1+\frac{1}{t^2}}\left(-\frac{1}{t^2}\right) d t
[x=\frac{1}{t} रखने पर]
-\int_0^1 \frac{\log \left(t+\frac{1}{t}\right)}{1+\frac{1}{t^2}} d t=-I
(2) से, हम रखते हैं:
2 I=\int_0^{\infty} \frac{\log \left(x+\frac{1}{x}\right)}{1+x^2} d x \\ I=\frac{1}{2} \int_0^{\infty} \frac{\log \left(1+x^2\right)-\log x}{1+x^2} d x \\ \Rightarrow I=\frac{\pi}{2} \log 2-\frac{1}{2} \int_0^{\infty} \frac{\log x}{1+x^2} d x [(1) से ]…..(3)
\int_c f(z) d z=\int_c \frac{\log z}{1+z^2} d z
जहाँ C परिरेखा है जिसमें शामिल है:
(1.)|z|=R ऊपरी अर्धतल में,एक बड़ा अर्धवृत \Gamma
(2.)वास्तविक अक्ष r से R
(3.)वास्तविक अक्ष -R से -r
(4.)एक छोटा अर्धवृत \gamma , |z|=r
z=\pm i ,f(z) के साधारण अनन्तक हैं,जिनमें केवल z=i, C के अन्दर स्थित है।
z=i पर अवशेष=\underset{z \rightarrow i}{\lim} (z-i) f(z) \\ =\underset{z \rightarrow i}{\lim} \frac{\log z}{z+i} \\=\frac{1}{2 i} \log e^{\frac{i \pi}{2}} \\=\frac{i\left(\frac{\pi}{2}\right)}{2 i}=\frac{\pi}{4}
अवशेष प्रमेय द्वारा,हम रखते हैं:
\int_c f(z) d z=\int_{\Gamma} f(z) d z+\int_R^r f\left(x e^{i \pi}\right) e^{i \pi} d x +\int_{\gamma} f(z) d z+\int_r^R f(x) d x=2 \pi i \Sigma R^{+} \cdots(4) \\ \left|\int_{\Gamma} f(z) d z\right| \leq \int_0^\pi\left|\frac{\log \left(R e^{i \theta}\right)}{R^2 e^{i 2 \theta}+1} R ie^{i \theta}\right| d \theta \\ \leq \int_0^\pi \frac{\log R+|i \theta|}{R^2-1} R d \theta \\ \leq \int_0^\pi \frac{(\log R+\theta)}{R^2-1} d \theta \\ =\left(\frac{\pi \log R+\frac{1}{2} \pi^2}{R^2-1}\right) R \\ =\frac{R^2}{R^2-1} \cdot\left[\pi \frac{\log R}{R}+\frac{\pi^2}{2 R}\right]
इसी प्रकार \left|\int_\gamma f(z) dz\right| \leq \int_{\pi}^0\left|\frac{\log \left(r e^{i \theta}\right)}{r^2 e^{i 2 \theta}+1}ri e^{i \theta}\right| d \theta \rightarrow 0 \text { as } r \rightarrow 0
इस प्रकार r \rightarrow 0, R \rightarrow \infty , (1) से रखते हैं:
\int_0^{\infty} f(x) d x-\int_{\infty}^0 f\left(x e^{i \pi}\right) d x=\frac{\pi^2}{2} i \\ \Rightarrow \int_0^{\infty} \frac{\log x}{1+x^2} d x+\int_0^{\infty} \frac{\log \left(x e^{i \pi}\right)}{1+x^2 e^{i 2 \pi}} d x=\frac{\pi^2}{2} i \\ \Rightarrow \int_0^{\infty} \frac{\log x}{1+x^2} d x+\int_0^{\infty} \frac{\log x+i \pi}{1+x^2} d x=\frac{i \pi^2}{2}
दोनों पक्षों के वास्तविक भागों की तुलना करने परः
2 \int_0^{\infty} \frac{\log x}{1+x^2} d x=0
यह मान (3) में रखने परः
\int_0^1 \frac{\log \left(x+\frac{1}{x}\right)}{1+x^2} d x=\frac{\pi}{2} \log 2
Illustration:3.सिद्ध कीजिए कि
\int_0^{\infty} \frac{x^{a-1}}{x^2+x+1} d x=\frac{2 \pi}{\sqrt{3}} \cos \left(\frac{2 a \pi+\pi}{6}\right) \operatorname{cosec} a \pi ,(0 < a< 2)
(Prove that)
\int_0^{\infty} \frac{x^{a-1}}{x^2+x+1} d x=\frac{2 \pi}{\sqrt{3}} \cos \left(\frac{2 a \pi+\pi}{6}\right) \operatorname{cosec} a \pi ,(0 < a< 2)
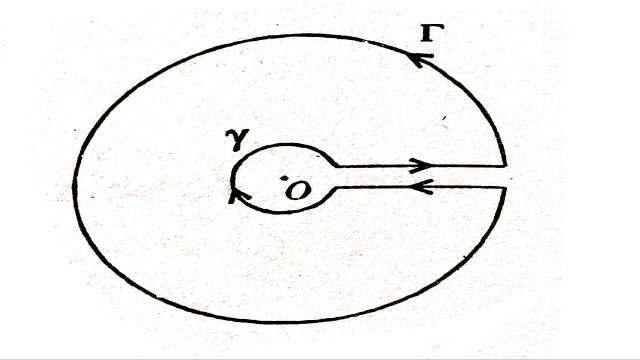
Solution: \int_c f(z) d z=\int_c \frac{z^{a-1}}{z^2+z+1} d z पर विचार करें,जहाँ C परिरेखा है जिसमें शामिल है:
(1.)एक बड़ा वृत्त \Gamma , |z|=R
(2.)त्रिज्या वेक्टर \theta=2 \pi
(3.)एक छोटा वृत्त \gamma , |z|=\rho
(4.)ध्रुवान्तर रेखा \theta=0
अवशेष प्रमेय द्वारा:
\int_C f(z) d z=\int_{\Gamma} f(z) d z+\int_R^\rho f\left(r e^{i 2 \pi}\right) e^{i 2 \pi} d r +\int_{\gamma} f(z) d z+\int_\rho^R f(x) d x=2 \pi i \Sigma R^{+} \cdots(1)
f(z) के अनन्तक दिए जाते हैं:
z^2+z+1=0 \Rightarrow z=\frac{-1 \pm i \sqrt{3}}{2} \\ z=-\frac{1}{2}+i \frac{\sqrt{3}}{2}=\alpha तथा z=-\frac{1}{2}-i \frac{\sqrt{3}}{2}=e^{\frac{i 4 \pi}{3}}=\beta
f(z) के साधारण अनन्तक हैं और दोनों C के अन्दर स्थित हैं:
z=\alpha पर अवशेष =\underset{z \rightarrow \alpha}{\lim} (z-\alpha) f(z) \\ =\underset{z \rightarrow \alpha}{\lim} \frac{z^{a-1}}{z-\beta}=\frac{\alpha^{a-1}}{\alpha-\beta}
C के अन्दर स्थित अवशेषों का योग
=\frac{\alpha^{a-1}}{\alpha-\beta}+\frac{\beta^{a-1}}{\beta-\alpha} \\ =\frac{1}{\alpha-\beta} \cdot\left(\alpha^{a-1}-\beta^{a-1}\right) \\ =\frac{1}{i \sqrt{3}}\left[e^{\frac{2 i \pi(a-1)}{3}}-e^{\frac{i 4 \pi(a-1)}{3}}\right] \\ =\frac{e^{i \pi(a-1)}}{i \sqrt{3}}\left[e^{-\frac{i \pi(a-1)}{3}}-e^{ \frac{i \pi(a-1)}{3}} \right] \\ =\frac{2 e^{i \pi a}}{\sqrt{3}} \sin \frac{(a-1) \pi}{3}=\frac{-2}{\sqrt{3}} e^{i \pi a} \cos \left[ \frac{\pi}{2}+(a-1) \frac{\pi}{3}\right] \\ =-\frac{2}{\sqrt{3}} e^{i a \pi} \cos \left(\frac{\pi+2 a \pi}{6}\right) \\ \left|\int_{\Gamma} f(z) d z\right| \leq \int_0^{2 \pi} \left| \frac{R^{a-1} \exp [i \theta(a-1)]}{1+R e^{i \theta}+R^2 e^{(2i \theta)}} i R e^{i \theta)} d \theta \right| \\ \leq \int_0^{2 \pi} \frac{R^a}{R^2-R-1} d \theta=\frac{2 \pi R^a}{R^2-R-1} \rightarrow 0 \text { as } R \rightarrow \infty \text {, since } 0 < a < 2
इसी प्रकार \left|\int_{\Gamma} f(z) d z\right| \leq \int_{2 \pi}^0 \frac{e^a}{1-\rho-\rho^2} d \theta \rightarrow 0 \text { as } \rho \rightarrow 0
जब R \rightarrow \infty, \rho \rightarrow 0 , (1) से रखते हैं:
\int_0^{\infty} f(x) d x+\int_{\infty}^0 f\left(r e^{i 2 \pi}\right) e^{i 2 \pi} d r=2 \pi i \Sigma R^{+} \\ \Rightarrow \int_0^{\infty} \frac{x^{a-1}}{1+x+x^2} d x-\int_0^{\infty} \frac{x^{a-1} e^{i(a-1) 2 \pi}}{1+x e^{i 2 \pi}+x^2 e^{i 4 \pi}} d x= 2 \pi i\left[-\frac{2}{\sqrt{3}}e^{i \pi a} \cos \left(\frac{\pi+2 a \pi}{6}\right)\right] \\ \Rightarrow \int_0^{\infty} \frac{x^{a-1}}{1+x+x^2}\left(1-e^{2 i a \pi}\right) d x= \frac{-4 \pi i}{\sqrt{3}} e^{i \pi a} \cos \left(\frac{\pi+2 a \pi}{6}\right) \\ \Rightarrow\left(\frac{e^{i a \pi} -e^{-i a \pi}}{2 i}\right) \int_0^{\infty} \frac{x^{a-1}}{1+x+x^2} d x=\frac{2 \pi}{\sqrt{3}} \cos \left( \frac{\pi+2 a \pi}{6}\right) \\ \Rightarrow \int_0^{\infty} \frac{x^{a-1}}{1+x+x^2} d x=\frac{2 \pi}{\sqrt{3}} \cos \left(\frac{\pi+2 a \pi}{6}\right) \operatorname{cosec} a \pi
Illustration:4.सिद्ध करो कि \int_0^{\infty} \frac{(\log x)^2}{x^2+x+1} d x=\frac{16 \pi^3}{81 \sqrt{3}}
(Prove that) \int_0^{\infty} \frac{(\log x)^2}{x^2+x+1} d x=\frac{16 \pi^3}{81 \sqrt{3}}
Solution: \int_c \frac{(\log z)^3}{z^2+z+1} d z=\int_c f(z) d z पर विचार करें,जहाँ C परिरेखा है जिसमें शामिल है:
(1.)एक बड़ा वृत्त |z|=R
(2.)त्रिज्य वेक्टर \theta=2 \pi
(3.)एक छोटा वृत्त \gamma , |z|=\rho
(5.)ध्रुवान्तर रेखा \theta=0
f(z) के अनन्तक है:
z^2+z+1=0 \Rightarrow z=\frac{-1 \pm i \sqrt{3}}{2} \\ z=-\frac{1}{2}+i \frac{\sqrt{3}}{2}=e^{\frac{2 \pi i}{3}}=\alpha या z=-\frac{1}{2}-i \frac{\sqrt{3}}{2}=e^{\frac{4 \pi i}{3}} =\beta
ये f(z) के साधारण अनन्तक हैं और दोनों C के अन्दर स्थित हैं।
\alpha-\beta=e^{\frac{2 \pi i}{3}}-e^{\frac{4 \pi i}{3}}=e^{i \pi}\left(e^{-\frac{i \pi}{3}}-e^{\frac{i \pi}{3}}\right) \\ \Rightarrow \alpha-\beta=(-1) \cdot\left(-2 i \sin \frac{\pi}{3}\right)=i \sqrt{3} \\ (\log \alpha)^3 -(\log \beta)^3=\left(\log e^{\frac{2 \pi i}{3}}\right)^3-\left(\log e^{\frac{4 \pi i}{3}}\right)^3 \\ =\left(\frac{2 \pi i}{3}\right)^3-\left(\frac{4 \pi i}{3}\right)^3 \\ \Rightarrow(\log \alpha)^3-(\log \beta)^3=\frac{56 \pi^3 i}{27}
z=\alpha पर अवशेष+ z=\beta पर अवशेष=\underset{z \rightarrow \alpha}{\lim} (z-\alpha) f(z)+\underset{z \rightarrow \beta}{\lim} (z-\beta) f(z) \\ =\underset{z \rightarrow \alpha}{\lim} \frac{(\log z)^3}{z-\beta}+\underset{z \rightarrow \beta}{\lim} \frac{(\log z)^3}{z-\alpha} \\ =\frac{(\log \alpha)^\beta-(\log \beta)^3}{\alpha-\beta} \\ =\frac{56 \pi^3 i}{27} \cdot \frac{1}{i \sqrt{3}}=\frac{56 \pi^3}{27 \sqrt{3}}
कोशी अवशेष प्रमेय सेः
\int_C f(z) d z=2 \pi i (C के अन्दर अवशेषों का योग)
=2 \pi i \cdot \frac{56}{27} \cdot \frac{\pi^3}{\sqrt{3}} \\ \Rightarrow \int_{\rho}^{R} f(x) d x+ \int_{\Gamma} f(z) d z+\int_R^{\rho} f\left(x \cdot e^{2 \pi i}\right) d\left(x e^{2 \pi i}\right) +\int_\gamma f(z) d z=\frac{112 \pi^4 i}{27 \sqrt{3}} \cdots(1) \\ \underset{z \rightarrow \infty}{\lim} z f(z)=\underset{z \rightarrow \infty}{\lim} \frac{(\log z)^3}{z+1+z^{-1}}=\underset{z \rightarrow \infty}{\lim} \frac{3(\log z)^2}{\left(1+0-z^{-2}\right)} [D L Hostital Rule से]
=\lim \frac{3(\log z)^2}{z-z^{-1}}=\lim \frac{6 \log z}{z\left(1+z^{-2}\right)}=\lim \frac{6 \log z}{z+z^{-1}} \\ \lim \frac{6}{z\left(1-z^{-2}\right)}=\underset{z \rightarrow \infty}{\lim} \frac{6 z}{z^2-1}=0
प्रमेय 2 से
\underset{R \rightarrow \infty}{\lim} \int_r f(z) d z=i(2 \pi-0)(0)=0 \\ \underset{z \rightarrow 0}{\lim} z f(z)=0, z=\frac{1}{t} रखने पर t \rightarrow \infty \text { as } z \rightarrow 0 \\ \underset{\rho \rightarrow 0}{\lim} \int_{\gamma} f(z) d z=-i(2 \pi-0) \cdot(0)=0
[प्रमेय \underset{R \rightarrow \infty}{\lim} f(z) d z=i\left(\theta_2-\theta_1\right) से जहाँ A= \underset{R \rightarrow \infty}{\lim} z f(z) ]
इस प्रकार जब R \rightarrow \infty, \rho \rightarrow 0 ,(1) सेः
\int_0^{\infty} f(x) d x+\int_{\infty}^{0} f\left(x e^{2 \pi i}\right) \cdot e^{2 \pi i} d x=\frac{112 \pi^4 i}{27 \sqrt{3}} \\ \Rightarrow \int_0^{\infty} \frac{(\log x)^3}{x^2+x+1} d x-\int_0^{\infty} \frac{\left(\log x e^{2 \pi i}\right)}{x^2+x+1}=\frac{112 \pi^4 i}{27 \sqrt{3}} \\ \Rightarrow \int_0^{\infty} \frac{(\log x+2 \pi i)^3-(\log x)^3}{x^2+x+1} d x=\frac{-112 \pi{ }^4 i}{2 \pi \sqrt{3}} \\ \Rightarrow \int_0^{\infty} \frac{(\log x)^3-8 \pi^3 i+6 \pi i(\log x)^2-12 \pi^2 \log -(\log x)^3}{x^2+x+1} dx=-\frac{112}{27 \sqrt{3}} \pi^4 i \\
{\left[\because(a+b)^3=a^3+b^3+3 a b(a+b)\right] }
दोनों पक्षों के काल्पनिक भागों की तुलना करने परः
\int_0^{\infty} \frac{-8 \pi^3+6 \pi(\log x)^2}{x^2+x+1} d x=-\frac{112 \pi^4}{27 \sqrt{3}} \\ \Rightarrow-6 \int_0^{\infty} \frac{(\log x)^2}{x^2+x+1} d x+8 \pi^2 \int_0^{\infty} \frac{d x}{x^2+x+1} =\frac{112 \pi^3}{27 \sqrt{3}} \cdots(4)
परन्तु \int_0^{\infty} \frac{d x}{x^2+x+1}=\int_0^{\infty} \frac{d x}{\left(x+\frac{1}{2}\right)^2 +\left( \frac{\sqrt{3}}{2}\right)^2}=\frac{1}{\frac{\sqrt{3}}{2}}\left[\tan ^{-1}\left(\frac{x+\frac{1}{2}}{\frac{\sqrt{3}}{2}}\right)\right]_0^{\infty} \\ =\frac{2}{\sqrt{3}}\left[\tan ^{-1} \infty-\tan ^{-1} \frac{1}{\sqrt{3}}\right] =\frac{2}{\sqrt{3}}\left(\frac{\pi}{2}-\frac{\pi}{6}\right) \\ \int_0^{\infty} \frac{d x}{x^2+x+1}=\frac{2 \pi}{3 \sqrt{3}}
(4) में इसका प्रयोग करने परः
-6 \int_0^{\infty} \frac{(\log x)^2 d x}{x^2+x+1} =\frac{112 \pi^3}{27 \sqrt{3}}-8 \pi^2 \cdot \frac{2 \pi}{3 \sqrt{3}} =-\frac{32 \pi^3}{27 \sqrt{3}} \\ \Rightarrow \quad \int_0^{\infty} \frac{(\log x)^2}{x^2+x+1} =\frac{16 \pi^3}{81 \sqrt{3}}
Illustration:5.मान ज्ञात करो \int_0^{\infty} \frac{\log x}{(1+x)^3} d x
(Evaluate) \int_0^{\infty} \frac{\log x}{(1+x)^3} d x
Solution: \int_c \frac{(\log z)^2}{(1+z)^3} d z=\int_c f(z) d z पर विचार करें,जहाँ C परिरेखा है जिसमें शामिल है:
(1.)एक बड़ा वृत्त \Gamma, |z|=R
(2.)त्रिज्या वेक्टर \theta=2 \pi
(3.)एक छोटा वृत्त \gamma , |z|=\rho
(4.)ध्रुवान्तर रेखा \theta=0
f(z) के अनन्तक हैं: (1+z)^3=0 \\ \Rightarrow z=-1,-1,-1
z=-1,f(z) तीन कोटि का अनन्तक है जो C के अन्दर हैं।
z=-1 पर अवशेष=\frac{\phi^{\prime \prime}(-1)}{2!}
जहाँ \phi(z)=(\log z)^2, f(z)=\frac{\phi(z)}{(1+z)^3} \\ \phi^{\prime}(z)=\frac{2}{z} \log z, \phi^{\prime \prime}(z) =2\left[-\frac{1}{z^2} \log z+\frac{1}{z^2}\right] \\ \phi^{\prime \prime}(-1) =2[1-\log (-1)]= 2\left[1-\log \left(e^{i \pi}\right)\right] \\ =2(1-i \pi)
z=-1 पर अवशेष=\frac{\phi^{\prime \prime}(-1)}{2}=1-i \pi
कोशी अवशेष प्रमेय द्वारा
\int_c f(z) d z=2 \pi i (C के अन्दर अनन्तकों पर अवशेषों का योग)=2 \pi(1-i \pi) \\ \Rightarrow \int^{\rho}_R f(x) d x+\int_{\Gamma} f(z) d z+\int_R^\rho f\left(x e^{2 \pi}\right) d\left(x e^{2 \pi i}\right) +\int_{\Gamma} f(z) d z=2 \pi(i+\pi) \cdots(1) \\ \underset{z \rightarrow \infty}{\lim} z f(z)=\left[\underset{z \rightarrow \infty}{\lim} \left(\frac{\log z}{z}\right)^2\right] \cdot \left[\underset{z \rightarrow \infty}{\lim} \frac{z^3}{(1+z)^3}\right]=0 \\ \underset{z \rightarrow \infty}{\lim} \int_{\Gamma} f(z) d z=i(2 \pi-0)(0)=0 \cdots(2)
[प्रमेय \underset{r \rightarrow \infty}{\lim} \int_c f(z) d z=i\left(\theta_2-\theta_1\right) A से,जहाँ A=\underset{r \rightarrow \infty}{\lim} z f(z) ]
जब R \rightarrow \infty, \rho \rightarrow 0 , (1) से रखते हैं:
\int_0^{\infty} f(x) d x+\int_{\infty}^0 f\left(x e^{2 \pi i}\right) \cdot e^{2 \pi i} d x=2 \pi(i+\pi) \\ \Rightarrow \int_0^{\infty} \frac{(\log x)^2}{(1+x)^3} d x-\int_0^{\infty} \frac{\left(\log x e^{2 \pi i}\right)^2}{(1+x)^3} d x=2 \pi(i+\pi) \\ \Rightarrow \int_0^{\infty} \frac{(\log x)^2-(\log x+2 \pi i)^2}{(1+x)^3} d x=2 \pi(i+\pi) \\ \Rightarrow \int_0^{\infty} \frac{-\left(-4 \pi^2+4 \pi i \log x\right)}{(1+x)^3} d x=2 \pi(i+\pi)
दोनों पक्षों के काल्पनिक भागों की तुलना करने परः
\int_0^{\infty} \frac{-4 \pi \log x}{(1+x)^3} d x=2 \pi \\ \Rightarrow \int_0^{\infty} \frac{\log x}{(1+x)^3} d x=\frac{1}{2}
Illustration:6.यदि,तब सिद्ध करो कि \int_0^{\infty} \frac{x^a}{\left(1+x^2\right)^2} d x=\frac{\pi(1-a)}{4 \cos \frac{1}{2} \pi a}
(Prove that,then \int_0^{\infty} \frac{x^a}{\left(1+x^2\right)^2} d x=\frac{\pi(1-a)}{4 \cos \frac{1}{2} \pi a} )
Solution: \int_c f(z) d z=\int_{c} \frac{z^a}{\left(1+z^2\right)^2} d z पर विचार करें,जहाँ C परिरेखा है जिसमें शामिल है:
(1.)एक बड़ा वृत्त \Gamma, |z|=R
(2.)त्रिज्या वेक्टर \theta= 2 \pi
(3.)एक छोटा वृत्त \gamma , |z|=\rho
(4.)ध्रुवान्तर रेखा \theta=0
z=\pm i ,f(z) के द्विक अनन्तक है और दोनों C के अन्दर स्थित हैं।
z=i पर अवशेष =\phi^{\prime}(i) जहाँ \phi(z)=\frac{z^a}{(z+i)^2} \\ \log \phi(z)=a \log z-2 \log (z+i) \\ \therefore \frac{\phi^{\prime}(z)}{\phi(z)}=\frac{a}{z}-\frac{2}{z+i} \\ \Rightarrow \phi^{\prime}(z)=\phi(z)\left[\frac{a}{z}-\frac{2}{z+i}\right] \\ \therefore \phi(i)=\frac{i a}{(2 i)^2} \cdot \frac{(a-1)}{i}=\frac{-(a-1)}{4 i} e^{\frac{i a \pi}{2}}\left[\because i=e^{\frac{i \pi}{2}}\right]
इस प्रकार z=i पर अवशेष =\phi^{\prime}(i)=-\frac{(a-1)}{4i} e^{\frac{i a \pi}{2}}
z=-i पर अवशेष=\psi^{\prime}(i) जहाँ \psi(z)=\frac{z^a}{(z-i)^2} \\ \therefore \varphi^{\prime}(z)=\psi(z)\left[\frac{a}{z}-\frac{z}{z-i}\right]
z=-i पर अवशेष
\varphi(i)=\frac{(-i)^a}{(-2 i)^2} \cdot \frac{(1-a)}{i}=-\frac{(1-a)}{4 i}\left(e^{i \pi} e^{\frac{i \pi}{2}}\right)^a
अवशेषों का योग=\frac{(a-1)}{4 i}\left[e^{i a \pi} e^{\frac{i a \pi}{2}}-e^{ \frac{i a \pi}{2}}\right] \\ =\frac{(a-1)}{4 i} e^{i a \pi}\left[e^{\frac{i a \pi}{2}}-e^{-\frac{i a \pi}{2}}\right] \\ =\frac{(a-1)}{2} e^{i a \pi} \sin \left(\frac{a \pi}{2}\right)
अवशेष प्रमेय द्वारा
\int_c f(z) d z=\int_{\Gamma} f(z) d z+\int_{\gamma}^R f(x) d x+\int_\gamma f(z) d z +\int_R^{\rho} f\left(r e^{i 2 \pi}\right) e^{i 2 \pi} d r=2 i \pi \Sigma R^{+} \cdots(1) \\ \left|\int_{\Gamma} f(z) d z\right| \leq \int_0^{2 \pi} \left|\frac{R^a e^i d \theta}{\left(1+R^2 e^{i 2 \theta}\right)^2} i R e^{i \theta} \right| d \theta \leq \int_0^{2 \pi} \frac{R^{a+1}}{\left(R^2-1\right)^2} d \theta=\frac{R^{a+1}}{\left(R^2-1 \right)^2} 2 \pi \rightarrow 0 as R \rightarrow \infty जबकि -1 < a< 3
इसी प्रकार \left|\int_{\gamma} f(z) d z\right| \leq \frac{\rho^{a+1}}{\left(1-\rho^2\right)^2} 2 \pi \rightarrow 0 as \rho \rightarrow 0
जब \rho \rightarrow 0 , R \rightarrow \infty ,(1) से रखते हैं
\int_0^{\infty} f(x) d x+\int_{\infty}^{\infty} f\left(r e^{i 2 \pi}\right) d r=2 \pi i \frac{(a-1)}{2} e^{i a \pi} \sin \frac{a \pi}{2} \\ \Rightarrow \int_0^{\infty} \frac{x^a}{\left(1+x^2\right)^2} d x-\int_0^{\infty} \frac{x^a e^{i 2 a} \pi}{\left(1+x^2\right)^2} d x=\pi i(a-1) e^{i a \pi} \sin \frac{a \pi}{2} \\ \Rightarrow \left(1-e^{i 2 a \pi}\right) \int_0^{\infty} \frac{x^a}{\left(1+x^2\right)^2} d x=i \pi(a-1) e^{i a \pi} \sin \frac{a \pi}{2} \\ \Rightarrow \int_0^{\infty} \frac{x^a}{\left(1+x^2\right)^2} d x=\frac{i \pi(1-a) \sin \left( \frac{a \pi}{2}\right)}{\left(e^{i a \pi}-e^{-c a \pi}\right)} \\ =\frac{\pi(1-a) \sin \left(\frac{a \pi}{2}\right)}{2 \sin a \pi} \\ =\frac{\pi(1-a) \sin \left(\frac{a \pi}{2}\right)}{4 \sin \left(\frac{a \pi}{2}\right) \cos \left( \frac{a \pi}{2}\right)} \\ \Rightarrow \int_0^{\infty} \frac{x^a}{\left(1+x^2\right)^2}=\frac{\pi(1-a)}{4 \cos \left(\frac{a \pi}{2}\right)}
उपर्युक्त उदाहरणों के द्वारा परिरेखा समाकलन विधि का प्रयोग करना (To Use Method of Contour Integration),परिरेखा समाकलन (Contour Integration) को समझ सकते हैं।
Also Read This Article:- Tips for Method of Contour Integration
3.परिरेखा समाकलन विधि का प्रयोग करना (Frequently Asked Questions Related To Use Method of Contour Integration),परिरेखा समाकलन (Contour Integration) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.परिरेखा समाकल सम्बन्धित प्रमेय का कथन क्या है? (What is the Statement of the Theorem Related with Contour Integration?):
उत्तर:मान लें कि AB वृत्त |z|=R का चाप \alpha \leq \theta \leq \beta है।यदि \underset{z \rightarrow \infty}{\lim} z f(z)=k तथा k अचर राशि है तो \underset{R \rightarrow \infty}{\lim} \int_{A B} f(z) d z=i(B-\alpha) k
यहाँ AB पर समाकलन वामावर्त दिशा में किया गया है।
प्रश्न:2.जोरदाँ उपप्रमेय का कथन लिखिए। (Write the Statement of the Jordan Lemma):
उत्तर:मान लें m > 0 तथा \gamma अर्धवृत |z|=R है तथा फलन f(z) निम्न प्रतिबन्धों को सन्तुष्ट करता है:
(i)f(z) ऊपरि अर्धतल में अनन्तकी फलन है;
(ii)जब |z| \rightarrow \infty तो 0 \leq \arg z \leq \pi के लिए f(z) एकसमानतः 0 की ओर अग्रसर होता है तो \underset{R \rightarrow \infty}{\lim} \int e^{i m z} f(z) d z=0
प्रश्न:3.अनन्तकों पर अवशेषों का योग के प्रमेय का कथन लिखो। (Write the Statement of the Theorem of the Sum of Residues of Poles):
उत्तर:यदि फलन निम्न प्रतिबन्धों को सन्तुष्ट करता है:
(1.)f(z) उपरि z-अर्धतल में अनन्तकी फलन है,
(2.)वास्तविक अक्ष पर f(z) के अनन्तक नहीं हैं,
(3.) 0 \leq \arg z \leq \pi के लिए z f(z) \rightarrow 0 एकसमानतः यथा |z| \rightarrow \infty ,
(4.) \therefore \int_0^{\infty} f(x) d x तथा \int^{\infty}_{-\infty} f(x) d x दोनों अभिसारी हैं,तो \int_{-\infty}^{\infty} f(x) d x=2 \pi i \Sigma R^{+} यहाँ पर \Sigma R^{+} फलन f(z) के उपर z-अर्धतल में स्थित अनन्तकों पर अवशेषों का योग है।
उपर्युक्त प्रश्नों के उत्तर द्वारा परिरेखा समाकलन विधि का प्रयोग करना (To Use Method of Contour Integration),परिरेखा समाकलन (Contour Integration) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here | |
| 7. | click here |
To Use Method of Contour Integration
परिरेखा समाकलन विधि का प्रयोग करना
(To Use Method of Contour Integration)
To Use Method of Contour Integration
परिरेखा समाकलन विधि का प्रयोग करना (To Use Method of Contour Integration) के इस
आर्टिकल में विभिन्न प्रकार के निश्चित समाकलों के मान निकालने के लिए दन्तुरण सहित या
दन्तुरण रहित वृत्ताकार परिरेखाओं का प्रयोग करके सवालों को हल करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.