Complex Integration in ComplexAnalysis
1.सम्मिश्र विश्लेषण में सम्मिश्र समाकलन (Complex Integration in ComplexAnalysis),सम्मिश्र समाकलन (Complex Integration):
सम्मिश्र विश्लेषण में सम्मिश्र समाकलन (Complex Integration in ComplexAnalysis) दो प्रकार से किया जाता है।किसी वक्र के अनुदिश सम्मिश्र चर राशि के फलन (या सम्मिश्र फलन) को समाकलन करने पर प्राप्त परिणाम शुद्ध (pure) एवं अनुपयुक्त (applied) गणित में विशेष महत्त्व रखते हैं।वास्तविक फलनों के समाकलनों पर दो प्रकार से विचार किया जा सकता है।प्रथम अवकलन की प्रतिलोम प्रक्रिया को अनिश्चित समाकलन तथा द्वितीय योग की सीमा को निश्चित समाकलन कहते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Conformal Mapping in Complex Analysis
2.सम्मिश्र विश्लेषण में सम्मिश्र समाकलन के साधित उदाहरण (Complex Integration in ComplexAnalysis Solved Examples):
Example:1.मान ज्ञात कीजिए (Evaluate):
Example:1(i). \int_a^b z^m d z जहाँ m एक धनात्मक पूर्णांक है तथा a एवं b दो सम्मिश्र संख्याएँ हैं।
(\int_a^b z^m d z Where m is a positive integers, a and b are any complex numbers.)
Solution: \int_a^b z^m d z \\ =\left[\frac{z^{m+1}}{m+1}\right]_a^b=\frac{1}{m+1}\left(b^{m+1}-a^{m+1}\right)
Example:1(ii). \int_C\left(z^2+1\right)^2 d z
जहाँ चक्रज x=a(\theta-\sin \theta) ; y=a(1-\cos \theta) का \theta=0 से 2 \pi तक का चाप है।
(Where C is arc of the cycloid x=a(\theta-\sin \theta) ; y=a(1-\cos \theta) from the point \theta=0 to 2 \pi)
Solution: \int_c\left(z^2+1\right)^2 d z \\ =\int_c\left(z^4+2 z^2+1\right) d z \\ =\int_c\left[(x+i y)^4+2(x+i y)^2+1\right] d(x+i y) \\=\int_0^{2 \pi}\left[\{a (\theta-\sin \theta)+i a(1-\cos \theta)\}^4+2 \{a(\theta-\sin \theta)+i a(1-\cos \theta)\}^2+1\right] \\ d\{a(\theta-\sin \theta)+i a(1-\cos \theta)\} \\
= \int_0^{2 \pi}\left[a^4\{\theta-\sin \theta+i(1-\cos \theta)\}^4+2 a^2 \{\theta-\sin \theta+i(1-\cos \theta)\}^2+1\right] \{1-\cos \theta+i \sin \theta) d \theta \\ \text { put } \theta-\sin \theta+i(1-\cos \theta)=t \\ (1-\cos \theta+i \sin \theta) d \theta=d t \\ = a \int_0^{2 \pi}\left[a^4 t^4+2 a^2 t^2+1\right] d t \\ = a\left[\frac{a^4 t^5}{5} +\frac{2 a^2 t^3}{3} +t\right]_0^{2 \pi} \\ =a\left[\frac{a^4}{5}\{\theta-\sin \theta+i(1-\cos \theta)\}^5+\frac{2 a^2}{3} \{\theta-\sin \theta+i(1-\cos \theta)\}^3+\{\theta-\sin \theta+i(1-\cos \theta\}\right]_{0}^{2 \pi} \\ = a\left[\frac{a^4}{5}\{2 \pi-\sin 2 \pi+i(1-\cos 2 \pi)\}^5 +\frac{2 a^2}{3} \right. \{2 \pi-\sin 2 \pi+i(1-\cos 2 \pi)\}^3+\{2 \pi-\sin 2 \pi+i(1-\cos 2 \pi)]-a\left[\frac{a^4}{5}\{\theta-\sin \theta+i(1-\cos \theta)^{5} \} +\frac{2 a^2}{3}\{0-\sin 0+i(1-\cos \theta)\}^3+\{0-\sin \theta +i(1-\cos 0)\right] \\ a\left[\frac{a^4}{5}(2 \pi)^5+\frac{2 a^2}{3}(2 \pi)^3+2 \pi\right] \\ =\frac{32 \pi^5 a^5}{5}+\frac{16 \pi^3 a^3}{3}+2 \pi a \\ =\frac{1}{15}\left(96 \pi^5 a^5+80 \pi^3 a^3+30 \pi a\right)
Example:1(iii). \int_0^{d+i}(z-1) dz परवलय y=x^2 के अनुदिश
(along the parabola y=x^2 )
Solution: \int_0^{1+i}(z-1) dz \\ f(z)=z-1, z=x+i y, z-1=x+i y-1 \\ dz=d x+i dy
इसका समाकलन दो निश्चित बिन्दुओं (0,0),(1,1) के बीच करना है जो z=0 तथा z=1+i के संगत है।
(1.)वास्तविक अक्ष का भाग (0,0) से (1,0) है।वास्तविक अक्ष पर y=0,z=x
(2.)यह भाग y काल्पनिक अक्ष के समान्तर है जो (1,0) से (1,1) के बीच है।इस पथ पर x=1 तथा y का मान 0 से 1 तक है।
z=x+i y=1+i y, d z=i d y \\ \int_0^{1+i}(z-1) d z=\int_0^{1+i}(x+i y-1) \cdot(d x+i d y) \\ =\int_0^{1}(x-1) d x+\int_0^1(iy)(i d y) \\ =\left[\frac{x^2}{2}-1\right]_0^1-\left[\frac{y^2}{2}\right]_0^1 \\ =\frac{1}{2}-1-\frac{1}{2}=-1
Example:2.निम्न वक्र के अनुदिश समाकलन का मान ज्ञात कीजिए।
(Evaluate the integral along the following curves)
\int_{(0,3)}^{(2,4)}\left(2 y+x^2\right) d x+(3 x-y) d y
Example:2(iii). रेखा (0,3) से (2,4) तक [a straight line from (0,3) to (2,4)]]
Solution: I=\int_{(0,3)}^{(2,4)}\left(2 y+x^2\right) d x+(3 x-y) d y
(0,3) से (2,4) को मिलनेवाली रेखा का समीकरण
y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right) \\ y-3=\frac{4-3}{2-0}(x-0) \\ \Rightarrow 2 y-6=x \\ \Rightarrow y=\frac{1}{2} x+3 \\ d y=\frac{1}{2} d x \\ I =\int_0^2\left[2\left(\frac{1}{2} x+3\right) +x^2\right] d x+\left(3 x-\frac{1}{2} x-3\right) \frac{1}{2} d x \\ =\int_0^2\left(x+6+x^2+\frac{5}{4}x-\frac{3}{2}\right) d x \\ =\int_0^2\left(\frac{9 x}{4}+x^2+\frac{9}{2}\right) dx \\ =\left[\frac{9 x^2}{8}+\frac{x^3}{3}+\frac{9 x}{2}\right]^2_{0} \\ =\left[\frac{9}{2}+\frac{8}{3}+9\right] \\ =\frac{27+16+54}{6} \\ =\frac{97}{6}
Example:3. \int_z \frac{d z}{(z-a)^n}, n=2,3,4 \ldots का मान ज्ञात करिये जबकि z=a एक संवृत्त वक्र C के अन्दर स्थित है।
(Evaluate \int_z \frac{d z}{(z-a)^n}, n=2,3,4 \ldots Where z=a is inside the simple closed curve C.)
Solution:-\int_z \frac{f(z)}{(z-a)^n} dz \\=\frac{2 \pi i}{(n-1) !} f^{(n-1)}(a)\left[f^n(z_{0})=\frac{n !}{2 \pi i}\int_{c} \frac{f(z) d z}{c(z-z_{0})^{n+1}} \text{ सूत्र से }\right] \\ f(z)=1, f^{(n-1)}(a)=0 \\ =\frac{2 \pi i}{(n-1) !} \times 0=0
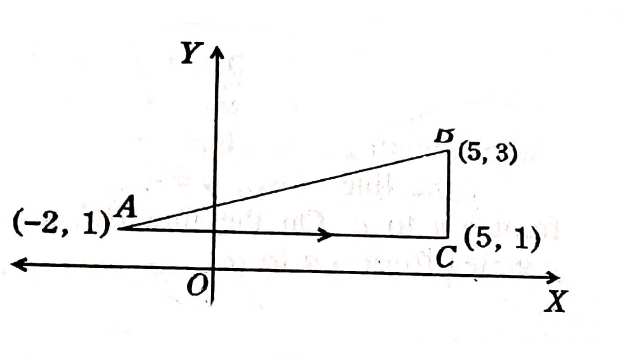
Example:7. \int_{-2+i}^{5+3 i} z^3 d z मान ज्ञात कीजिए (Evaluate \int_{-2+i}^{5+3 i} z^3 d z )
Solution: \int_{-2+i}^{5+3 i} z^3 d z
(-2,1) तथा (5,3) से गुजरने वाली रेखा का समीकरण
y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right) \\ \Rightarrow y-1=\frac{3-1}{5+2}(x+2) \\ \Rightarrow y=\frac{2}{7} x+\frac{4}{7}+1 \\ \Rightarrow y=\frac{2}{7} x+\frac{11}{7} \\ d y=\frac{2}{7} d x \\ =\int_{-2+i}^{5+3 i}(x+i y)^3 d(x+i y) \\ =\int_{-2}^5\left(x+\frac{2}{7} i x+\frac{11}{7} i\right)^3(d x+i d y) \\ =\int_{-2}^5\left(x+\frac{2}{7} i x+\frac{11}{7} i\right)^3\left(d x+\frac{2 i}{7} d x\right) \\=\int_{-2}^5 \left(x+\frac{2}{7} i x+\frac{11}{7} i\right)^3\left(1+\frac{2 i}{7}\right) d x \\ \text{ put } x+\frac{2}{7}i x+\frac{11}{7} i=t \\ \Rightarrow \left(1+\frac{2}{7} i\right) d x=d t
जब x=-2 तो t=-2+i
जब x=5 तो t=5+3i
=\int_{-2+i}^{5+3i} t^3 d t \\ =\left[\frac{t^4}{4}\right]^{5+3i} \\ =\frac{1}{4}\left[(5+3 i)^4-(-2+i)^4\right] \\ =\frac{1}{4}\left[\left\{(5+3 i)^2-(-2+i)^2\right\}\left\{(5+3 i)^2+(-2+i)^2\right\}\right] \\ =\frac{1}{4}[(25-9+30 i-4+1+4 i)(25-9+30 i+4-1-4i)] \\ =\frac{1}{4}[(13+34 i)(19+26 i)] \\ =\frac{1}{4}(247+338 i+646 i-884) \\ =\frac{1}{4}(-637+984 i) \\ \int_{-2+i}^{5+3 i} z^3 d z=\int_{A C} z^3 d z+\int_{C B} z^3 d z \\ =\int_{-2}^5(x+i)^3 d x+\int_1^3(3+i y)^3 i d y \\ =\left[\frac{(x+i)^4}{4}\right]_{-2}^5 +\left[\frac{(3+i y)^4}{4}\right]_1^3 \\ =\frac{1}{4}\left[\left(5+i)^4(-2+i)^4+(3+3 i)^4-(3+i)^4\right]\right. \\ =\frac{1}{4}\left[(5+i)^2-(-2+i)^2\right\}\left\{(5+i)^2+(-2+i)^2\right\}+\left.\left\{(3+3 i)^2-(3+i)^2 \right\}\left\{\left(3-Bi\right)^2+(3+i)^2\right\}\right] \\ = \frac{1}{4}[(25+10 i-1-4+1+4 i)(25+10 i-1+4-1-4 i)+(9-9+18 i-9-6 i+1)(9-9+18 i +9-1+6 i)] \\ =\frac{1}{4}[(21+14 i)(27+6 i)+(12 i-8)(24 i+8)] \\ \left.=\frac{1}{4}[567+126 i+378 i-84-288+96 i-192 i-64)\right] \\ =\frac{1}{4}[131+408 i)
Alternate:
(1.)वास्तविक अक्ष के समान्तर रेखा AC बिन्दु A(-2,1) से C(5,1) तक, AC पर y=1,dy=0 तथा x का मान – 2 से 5 तक परिवर्तित होता है।
(2.)काल्पनिक अक्ष के समान्तर रेखा CB बिन्दु C(5,1) से B(5,3) तक।इस रेखा पर x=3,dx=0 और y का मान 1 से 3 तक परिवर्तित होता है।
Example:8.मान ज्ञात कीजिए (Evaluate):
\int_e(\bar{z})^2 d z
जहाँ C निम्न वृत्त है
(Where C are following circles):
Example:8(i). |z|=1
Solution: |z|=1 वृत्त की त्रिज्या 1 है तथा केन्द्र (0,0) है।
z=e^{i \theta} तथा d z=i e^{i \theta} d \theta \\ \bar{z}=e^{-i \theta} \\ \int_c(\bar{z})^2 d z =\int_0^{2 \pi} e^{-2 i \theta} \cdot i e^{i \theta} d \theta \\ =i \int_0^{2 \pi} e^{-i \theta} d \theta \\ =-\left[e^{-i \theta}\right]_0^{2 \pi} \\ = -\left(e^{-2 \pi i}-e^0\right) \\ = 1-(\cos 2 \pi-i \sin 2 \pi) \\ = 0
Example:8(ii).|z-1|=1
Solution: वृत्त का केन्द्र (1,0) तथा त्रिज्या 1 है।
इस वृत्त पर z-1=e^{i \theta} \Rightarrow z=1+e^{i \theta} तथा dz=i e^{i \theta} d \theta \\ \int_c(\bar{z})^2 d z=\int_0^{2 \pi} \left(1+e^{-i \theta}\right)^2 i e^{i \theta} d \theta \\ =\int_0^{2 \pi}\left(1+2 e^{-i \theta}+e^{-2 i \theta}\right) i e^{i \theta} d \theta \\ =i \int_0^{2 \pi}\left(e^{i \theta}+2+e^{-i \theta}\right) d \theta \\ =i\left[\frac{e^{i \theta}}{i}+2 \theta+\frac{e^{-i \theta}}{-i}\right]_0^{2 \pi} \\ =\left[\left(e^{2 \pi i}+4 \pi i-e^{-2 \pi i}\right)-(1+0-1)\right] \\ =\cos 2 \pi+i \sin 2 \pi+4 \pi i-\cos 2 \pi+i \sin 2 \pi \\ =4 \pi i
Example:9.मान ज्ञात कीजिए (Evaluate):
\int \left(x^2-i y^2\right) d z जहाँ (Where)
Example:9(i).C परवलय को बिन्दुओं (1,1) तथा (2,8) को मिलाने वाला वक्र है।
(C is parabola joining the points (1,1) and (2,8).)
Solution: z=x+i y \\ d z=d x+i d y \\ y=2 x^2, d y=4 x d x \\ \left(x^2-i y^2\right) dz=\left[x^2-i\left(4 x^4\right)\right][d x+i 4x dx] \\ =\left(x^2 dx+16 x^5 d x\right)+i \left(i 4x^3 d x-4 x^4\right) dx \\ =\left(x^2+16 x^5\right) d x+i\left(4 x^3-4 x^4\right) dx \\ \int_{c} \left(x^2-i y^2\right) dy=\int_{1}^{2} \left[\left(x^2 dx+16 x^5 \right)+i \left(4x^3-4 x^4\right)\right] dx \\ =\left[\left(\frac{x^3}{3}+\frac{16 x^6}{6}\right)+i\left(\frac{4 x^4}{4}-\frac{4}{5} x^5\right)\right]_1^2 \\ =\left[\frac{8}{3}+\frac{512}{3}+i\left(\frac{64}{4}-\frac{128}{5}\right)\right]-\left[\frac{1}{3}+\frac{16}{6}+i \left(1-\frac{4}{5}\right) \right] \\ =\left(\frac{520}{3}-\frac{48 i}{5}\right)-\left(\frac{9}{3}+\frac{1}{5} i\right) \\ =\frac{511}{3}-\frac{49}{5} i
Example:9(ii).सरल रेखा (1,1) से (1,8) तत्पश्चात (1,8) से (2,8) तक
(Straight lines from (1,1) to (1,8) and then (1,8) to (2,8).)
Solution: z=x+i y \Rightarrow d z=d x+i d y \\ x=1 \Rightarrow d x=0 तथा y=1 से y=8
\int_C\left(x^2-i y^2\right) d z=\int_1^8\left(1-i y^2\right) i dy \\=i\left[y-i \frac{y^3}{3}\right]^8 \\ =i\left[8-\frac{512 i}{3}-1+\frac{i}{3}\right] \\ =i\left(7-\frac{511 i}{3}\right)=7 i+\frac{511}{3}
जब रेखा (1,8) से (2,8) तक हो
y=8 \Rightarrow dy=0 तथा x=1 से x=2
\int_c\left(x^2-i y^2\right) d z=\int_1^2\left(x^2-64 i\right) d x \\ =\left[\frac{x^3}{3}-64 x i\right]_1^2 \\ =\frac{8}{3}-128 i-\frac{1}{3}+64 i \\ =\frac{7}{3}-64 i \\ =\frac{54}{3}+7 i+\frac{7}{3}-64 i \\ =\frac{518}{3}-57 i
Example:10.यदि C एक वर्ग है जिसके शीर्ष 1 \pm i, -1 \pm i हैं तो फलन 3 z^{2}+i z-4 के लिए कोशी प्रमेय का सत्यापन करिये।
(If C is a square with vertices 1 \pm i, -1 \pm i then verify the cauchy’s theorem for the function 3 z^{2}+i z-4)
Solution:यहाँ f(z)=3 z^{2}+i z-4 \\ \therefore \int_e f(z) d z=\int_e\left(3 z^2+i z-4\right) dz \\ =\int_{A B}\left(3 z^2+i z-4\right) d z+\int_{B C}(3 z+i z-4) d z +\int\left(3 z^2+i z-u\right) d z+\int_{D A}\left(3 z^2+i z-4\right) dz
z=x+iy तथा dz=dx+idy
अब AB पर x=1,dx=0 तथा y का मान -1 से 1 तक होगा
अब BC पर y=1,dy=0 तथा x का मान 1 से -1 तक होगा
अब CD पर x=-1,dx=0 तथा y का मान 1 से -1 तक होगा
अब DA पर y=-1,dy=0 तथा x का मान -1 से 1 तक होगा।
\therefore \int_c f(z) d z=\int_{-1}^1\left[3(1+i y)^2+i(1+i y)-4\right] i dy +\int_1^{-1} \left[3(x+i)^2 + i(x+i)-4 \right] dx+ \int_1^{-1}\left[3(-1+i y)^2+i(-1+i y)-4\right] i dy+\int_{-1}^1\left[3(x-i)^2+i(x-i)-4\right] dx \\= i\left[\frac{1}{i}(1+i y)^3+\frac{(1+i y)^2}{2}-4 y\right]_{-1}^1+\left[(x+i)^3 +\frac{i(x+i)^{2}}{2}-4 x\right]_1^{-1}+i\left[\frac{1}{i}(-1+i y)^3+\frac{(-1+i y)^2}{2}-4 y\right]_{1}^{-1} +\left[(x-i)^3+i \frac{(x-i)^2}{2}-4 x\right]_{-1}^1 \\ =\frac{i(1+i)^3}{i}+\frac{i(1+i)^2}{2}-4 i-\frac{i}{i}(1-i)^3-\frac{i(1-i)^2}{2}-4 i+(-1+i)^3+\frac{i(-1+i)^{2}}{2}+4-(1+i)^3 -\frac{i(1+i)^2}{2}+4+\frac{i^2}{2}(-1-i)^3+i(-1-i)^2 + 4 i-\frac{i}{i}(-1+i)^3-\frac{i(-1+i)^2}{2}+4 i+(1-i)^3+\frac{i(1-i)^2}{2}-4-(-1-i)^3-\frac{i(-1-i)^2}{2}-4 \\= (1+i)^3 +\frac{i(1+i)^2}{2}-4 i-(1-i)^3-\frac{i(1-i)^2}{2}-4 i+(-1+i)^3 +\frac{i(-1+i)^{2}}{2}+4-(1+i)^3 -\frac{i(1+i)^2}{2}+4+(-1-i)^3+\frac{i(-1-i)^2}{2}+4 i-(-1+i)^3-\frac{i(-1+i)^2}{2}+4 i+(1-i)^3 +i \frac{(1-i)^2}{2}-4-(-1-i)^3 -\frac{i(-1-i)^2}{2}-4\\ =0
अतः कन्टूर C पर कोशी समाकल प्रमेय सत्यापित हुई।
Example:11.मान ज्ञात कीजिए (Evaluate):
\int_c \frac{d z}{z-a}
जहाँ C कोई सरल संवृत्त वक्र है एवं बिन्दु z=a बाहर है।
(Where C is any simple closed curve and z=a is point outside C.)
Solution: \int_c \frac{d z}{z-a}
बिन्दु z=a,वक्र के बाहर है।अतः फलन f(z) वृत्त के अन्दर तथा परिधि पर स्थित सभी बिन्दुओं पर विश्लेषिक फलन होगा फलतः कोशी प्रमेय सेः
\int_c \frac{d z}{z-a}=0
उपर्युक्त उदाहरणों के द्वारा सम्मिश्र विश्लेषण में सम्मिश्र समाकलन (Complex Integration in ComplexAnalysis),सम्मिश्र समाकलन (Complex Integration) को समझ सकते हैं।
3.सम्मिश्र विश्लेषण में सम्मिश्र समाकलन पर आधारित सवाल (Questions Based on Complex Integration in ComplexAnalysis):
(1.)वृत्त |z|=2 के अनुसार (2,0) से (0,2) तक \int_C\left(z^2+3 z\right) d z का मान ज्ञात करो।
(Evaluate \int_C\left(z^2+3 z\right) d z along the circle |z|=2 from (2,0) to (0,2).)
(2.)मान ज्ञात करो \int_c f(z) d z जहाँ f(z)=y-x-3x^2 i तथा C रेखाखण्ड z=0 से z=1+i है।
(Evaluate \int_c f(z) d z where f(z)=y-x-3 x^2 i and C is the line segment from z=0 to z=1+i.)
उत्तर (Answers): (1.) -\left(\frac{44}{3}+\frac{8 i}{3}\right)
(2.)1-i
उपर्युक्त सवालों को हल करने पर सम्मिश्र विश्लेषण में सम्मिश्र समाकलन (Complex Integration in ComplexAnalysis),सम्मिश्र समाकलन (Complex Integration) को ठीक से समझ सकते हैं।
Also Read This Article:-Bilinear Transformation
4.सम्मिश्र विश्लेषण में सम्मिश्र समाकलन (Frequently Asked Questions Related to Complex Integration in ComplexAnalysis),सम्मिश्र समाकलन (Complex Integration) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.सम्मिश्र विश्लेषण में कंटूर किसे कहते हैं? (What is Contour in Complex Analysis?)
Solution:परिमित संख्या में नियमित चापों के संतत श्रृंखला (Chain) से बनने वाले जोरदाँ वक्र को कन्टूर कहते हैं।
प्रश्न:2.सम्मिश्र विश्लेषण में कोशी का मूल प्रमेय क्या है? (What is Cauchy’s Integral Theorem in Complex Analysis?):
Solution:प्रमेय (Theorem):माना कि एकशः संबद्ध प्रदेश G में f(z) विश्लेषिक फलन है तथा f'(z) संतत है।यदि G में C एक संवृत्त कंटूर हो तो
\int_c f(z) d z=0
(Let f(z) is analytic with a continuous derivative in a simply connected in G,then \int_c f(z) d z=0 )
उपपत्ति (Proof):माना f(z)=u(x,y)+iv(x,y)
तथा z=x+i y \Rightarrow d z=d x+i dy तो
\int_{c} f(z) d z=\int_c(u+i v) \cdot(d x+i d y) \\ =\int_{c} (u d x-v d y)+i \int_c(u d x+v d y) \cdots(1)
विश्लेषिक फलन के लिए कोशी रीमान समीकरणों
f^{\prime}(z)=u_x+i v_x=v_y-i u_{y} \cdots(2)
चूँकि f'(z) संतत है अतः G में चारों आंशिक अवकलज u_x,u_y, v_x और v_y संतत होंगे।फलतः ग्रीन प्रमेय से जिसका कथन हैः
\int_c P d x+Q d y=\iint_{G} \left(\frac{\partial Q}{\partial x}+\frac{\partial P}{\partial y}\right) dx dy \cdots(3)
[जहाँ P=u(1+i),Q=v(i-1)]
हमें प्राप्त होगा
\int_C f(z) d z=\iint_{G}\left(\frac{\partial v}{\partial x}+\frac{\partial y}{\partial y}\right) d x d y+i \iint_{G}\left(\frac{\partial v}{\partial x}-\frac{\partial y}{\partial y}\right) dxdy \\ =-\iint_{G} \left(\frac{\partial v}{\partial x}-\frac{\partial v}{\partial v}\right) d x d y+i \iint_G\left(\frac{\partial v}{\partial y}-\frac{\partial v}{\partial y}\right) \\ =0(कोशी रीमान समीकरणों से)
प्रश्न:3.सम्मिश्र फलनों के लिए समाकलन का मूल प्रमेय क्या है? (What is Fundamental Theorem of Integral Calculus in Complex Functions?):
Solution:प्रकथन:माना एक एकशः सम्बद्ध प्रान्त G में f(z) एक बहुमानी विश्लेषिक फलन है।यदि a, b \in G तब
\int_a^b f(x) dx=\phi(b)-\phi(a)
यहाँ \phi(z), f(z) का अनिश्चित समाकल है।
(Statement:Let f(z) be a single valued analytic function in a simple connected domain G.If a, b \in G, then
\int_a^b f(x) dx=\phi(b)-\phi(a)
Where \phi(z) is an indefinite integral of f(z).)
उपपत्ति (Proof):माना F(a)=\int_{z_{0}}^{z} f(t) d t \cdots(1)
f(z) का अनिश्चित समाकल \phi(z) हो तो
\phi(z)=F(z)+kजहाँ k अचर है।…….(2)
(2)से \phi(b)=F(b)+k एवं \phi(a)=F(a)+k
अतः \phi(b)-\phi(a)=\left\{F(b)+k \right\}-\left\{ F(a)+k \right\}
या \phi(b)-\phi(a)=F(b)-F(a) \cdots(3)
अब समीकरण (1) सेः
F(b)=\int_{z_0}^b f(t) d t तथा F(a)=\int_{z_{0}}^{a} f(t) d t
अब F(b)-F(a)=\int_{z_{0}}^{b} f(t) d t-\int_{z_{0}}^{a} f(t) d t \\ =\int_{z_0}^b f(t) d t+\int_a^{z_{0}} f(t) d t \\=\int_a^b f(t) d t=\int_a^b f(t) d z
या \Rightarrow \phi(b)-\phi(a)=\int_a^b f(z) d z
उपर्युक्त प्रश्नों के उत्तर द्वारा सम्मिश्र विश्लेषण में सम्मिश्र समाकलन (Complex Integration in ComplexAnalysis),सम्मिश्र समाकलन (Complex Integration) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Complex Integration in ComplexAnalysis
सम्मिश्र विश्लेषण में सम्मिश्र समाकलन
(Complex Integration in ComplexAnalysis)
Complex Integration in ComplexAnalysis
सम्मिश्र विश्लेषण में सम्मिश्र समाकलन (Complex Integration in ComplexAnalysis) दो प्रकार
से किया जाता है।किसी वक्र के अनुदिश सम्मिश्र चर राशि के फलन (या सम्मिश्र फलन) को समाकलन
करने पर प्राप्त परिणाम शुद्ध (pure) एवं अनुपयुक्त (applied) गणित में विशेष महत्त्व रखते हैं।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.