Direction Cosines Class 12
1.रेखा के दिक्-कोसाइन कक्षा 12 (Direction Cosines Class 12),कक्षा 12 में रेखा के दिक्-कोसाइन (Direction Cosines in Class 12):
रेखा के दिक्-कोसाइन कक्षा 12 (Direction Cosines Class 12) के इस आर्टिकल में रेखाओं के दिक्-कोसाइन ज्ञात करने के लिए सवालों को हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Product of Two Vectors in Class 12
2.रेखा के दिक्-कोसाइन कक्षा 12 के उदाहरण (Direction Cosines Class 12 Examples):
Example:1.यदि एक रेखा x,y और z-अक्ष के साथ क्रमशः 90°,135°,45° के कोण बनाती है तो इसकी दिक्-कोसाइन ज्ञात कीजिए।
Solution: l=\cos \alpha=\cos 90^{\circ}=0 \\ m=\cos \beta=\cos 135^{\circ}=\cos \left(98^{\circ}+45^{\circ}\right) \\ \Rightarrow m=\cos \beta=-\sin 45^{\circ}=-\frac{1}{\sqrt{2}} \\ n=\cos \gamma=\cos 45^{\circ}=\frac{1}{\sqrt{2}}
अतः रेखा के दिक्-कोसाइन: 0,-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}
Example:2.एक रेखा की दिक्-कोसाइन ज्ञात कीजिए जो निर्देशांक्षों के साथ समान कोण बनाती है।
Solution:रेखा अक्षों के साथ समान कोण बनाती है अतः \alpha=\beta=\gamma \\ l^2+m^2+n^2=1 \\ \Rightarrow \cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma=1 \\ \Rightarrow \cos ^2 \alpha+\cos ^2 \alpha+\cos ^2 \alpha=1 \\ \Rightarrow 3 \cos ^2 \alpha=1 \Rightarrow \cos ^2 \alpha=\frac{1}{3} \\ \Rightarrow \cos \alpha= \pm \frac{1}{\sqrt{3}}
अतः रेखा के दिक्-कोसाइनः \pm \frac{1}{\sqrt{3}}, \pm \frac{1}{\sqrt{3}}, \pm \frac{1}{\sqrt{3}}
Example:3.यदि एक रेखा के दिक्-अनुपात -18,12,-4 हैं तो इसकी दिक्-कोसाइन क्या हैं?
Solution:a=-18,b=12,c=-4
\sqrt{a^2+b^2+c^2} =\sqrt{(-18)^2+12^2+(-4)^2} \\ =\sqrt{324+144+16} \\ \Rightarrow \sqrt{a^2+b^2+c^2} =\sqrt{484}=22
अतः रेखा की दिक्-कोसाइनः l=\frac{a}{\sqrt{a^2+b^2+c^2}}=\frac{-18}{22}=\frac{-9}{11} \\ m=\frac{b}{\sqrt{a^2+b^2+c^2}}=\frac{12}{22}=\frac{6}{11} \\ n=\frac{c}{\sqrt{a^2+b^2+c^2}}=-\frac{4}{22}=-\frac{2}{11}
अतः दिक्-कोसाइन \frac{-9}{11}, \frac{6}{11},-\frac{2}{11}
Example:4.दर्शाइए कि बिन्दु (2,3,4),(-1,-2,1),(5,8,7) संरेख हैं।
Solution:माना A(2,3,4),B(-1,-2,1),C(5,8,7)
AB की दिक्-कोसाइनः
\frac{x_2-x_1}{P Q}, \frac{y_2-y_1}{P Q}, \frac{z_2-z_1}{P Q} \\ l_1=\frac{-1-2}{\sqrt{(-1-2)^2+(-2-3)^2+(1-4)^2}} \\ =\frac{-3}{\sqrt{(-3)^2+(-5)^2+(-3)^2}}=\frac{-3}{\sqrt{9+2519}} \\ \Rightarrow l_1=\frac{-3}{\sqrt{43}} \\ m_1=\frac{-2-3}{\sqrt{43}}=\frac{-5}{\sqrt{43}} \\ n_1=\frac{1-4}{\sqrt{43}}=\frac{-3}{\sqrt{43}}
अतः AB की दिक्-कोसाइनः \frac{-3}{\sqrt{43}}, \frac{-5}{\sqrt{43}}, \frac{-3}{\sqrt{43}}
BC की दिक्-कोसाइनः
l_2=\pm \frac{5+1}{\sqrt{(5+1)^2+(8+2)^2+(7-1)^2}} \\ =\pm \frac{6}{\sqrt{36+100+36}}= \pm \frac{6}{\sqrt{172}} =\pm \frac{3}{\sqrt{43}} \\ \Rightarrow l_2 =-\frac{3}{\sqrt{43}} \\ m_2= \pm \frac{8+2}{\sqrt{172}}= \pm \frac{10}{2 \sqrt{43}} \\ \Rightarrow m_2=-\frac{5}{\sqrt{43}} , \\ n_2= \pm \frac{7-1}{\sqrt{172}}= \pm \frac{6}{2 \sqrt{43}} \Rightarrow n_2=\frac{-3}{\sqrt{43}}
BC की दिक्-कोसाइनः -\frac{3}{\sqrt{43}}, \frac{-5}{\sqrt{43}}, -\frac{3}{\sqrt{43}}
अतः l_{1}=l_{2} , m_{1}=m_{2} , n_{1}=n_{2}
दिक्-कोसाइन समान है फलतः बिन्दु संरेख है।
Example:5.एक त्रिभुज की भुजाओं की दिक्-कोसाइन ज्ञात कीजिए यदि त्रिभुज के शीर्ष बिन्दु (3,5,-4),(3,5,-4) और (-5,-5,-2) हैं।
Solution:माना A(3,5,-4),B(3,5,-4) और C(-5,-5,-2)
AB के दिक्-कोसाइन:
\frac{x_2-x_1}{A B}, \frac{y_2-y_1}{A B}, \frac{z_2-z_1}{A B}\\ x_2-x_1=-1-3=-4, y_2-y_1=1-5=-4 , z_2-z_1=2+4=6 \\ AB=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2} \\ =\sqrt{(-4)^2 +(-4)^2+(6)^2}=\sqrt{16+16+36}=\sqrt{68} \\ \Rightarrow A B=2 \sqrt{17}
अतः AB के दिक्-कोसाइन: l_{1}=\frac{-4}{2 \sqrt{17}}=\frac{-2}{\sqrt{17}}, m_1=\frac{-4}{2 \sqrt{17}}=\frac{2}{\sqrt{17}} ,n_1=\frac{6}{2 \sqrt{17}}=\frac{3}{\sqrt{17}} \\ =-\frac{2}{\sqrt{17}},-\frac{2}{\sqrt{17}}, \frac{3}{\sqrt{17}}
BC के दिक्-कोसाइन:
\frac{x_3-x_2}{B C}, \frac{y_3-y_2}{B C}, \frac{z_3-z_2}{B C} \\ x_3-x_2=-5+1=-4, y_3-y_2=-5-1=-6, z_3-z_2=-2-2=-4 \\ BC=\sqrt{\left(y_3-x_2\right)^2+\left(y_3-y_2\right)^2+\left(z_3-z_2\right)^2} =\sqrt{(-4)^2+(-6)^2+(-4)^2} \\ \Rightarrow BC=\sqrt{16+36+16}=\sqrt{68}=2 \sqrt{17}
अतः BC के दिक्-कोसाइन:
l_{2}=\frac{-4}{2 \sqrt{17}}=-\frac{2}{\sqrt{17}} , m_{2}=\frac{-6}{2 \sqrt{17}}=-\frac{3}{\sqrt{17}} , n_2=\frac{-4}{2 \sqrt{17}}=-\frac{2}{\sqrt{17}} \\ =-\frac{2}{\sqrt{17}},-\frac{3}{\sqrt{17}} ,-\frac{2}{\sqrt{17}}
CA के दिक्-कोसाइन: \frac{x_1-x_3}{C A}, \frac{y_1-y_3}{C A}, \frac{z_1-z_3}{C A} \\ x_1-x_3=3+5=8, y_{1}-y_3=5+5=10, z_1-z_3=-4+2=-2 \\ CA=\sqrt{\left(x_1-x_3\right)^2+\left(y_1-y_3\right)^2+\left(z_1-z_3\right)^2}=\sqrt{(8)^2+(10)^2+(-2)^2} \\ \Rightarrow C A=\sqrt{64+100+4}=\sqrt{168}=2 \sqrt{42}
अतः CA के दिक्-कोसाइन:
l_3=\frac{8}{2 \sqrt{42}}=\frac{4}{\sqrt{42}} \\ m_3=\frac{10}{2 \sqrt{42}}=\frac{5}{\sqrt{42}}, n_3=\frac{-2}{2 \sqrt{42}}=-\frac{1}{\sqrt{42}} \\ =\frac{4}{\sqrt{42}}, \frac{5}{\sqrt{42}},-\frac{1}{\sqrt{42}}
उपर्युक्त उदाहरणों के द्वारा रेखा के दिक्-कोसाइन कक्षा 12 (Direction Cosines Class 12),कक्षा 12 में रेखा के दिक्-कोसाइन (Direction Cosines in Class 12) को समझ सकते हैं।
3.रेखा के दिक्-कोसाइन कक्षा 12 के सवाल (Direction Cosines Class 12 Questions):
(1.)सिद्ध कीजिए कि बिन्दु A(3,-5,1),B(-1,0,8) और C(7,-10,-6) संरेख हैं।
(2.)यदि O मूलबिन्दु हो और दो बिन्दु P(2,3,4) एवं Q(1,-2,1) हैं।सिद्ध कीजिएः OP \perp OQ
उपर्युक्त सवालों को हल करने पर रेखा के दिक्-कोसाइन कक्षा 12 (Direction Cosines Class 12),कक्षा 12 में रेखा के दिक्-कोसाइन (Direction Cosines in Class 12) को ठीक से समझ सकते हैं।
Also Read This Article:- Vector Product of Two Vectors Class 12
4.दो बिन्दुओं को मिलाने वाली रेखा की दिक्-कोसाइन (Direction Cosines of a Line Passing Through Two Points):
क्योंकि दो बिन्दुओं से होकर जाने वाली रेखा अद्वितीय होती है।इसलिए दो दिए गए बिन्दुओं P(x_1,y_1,z_1) और Q(x_2,y_2,z_2) से गुजरने वाली रेखा की दिक्-कोसाइन को निम्न प्रकार ज्ञात करते हैं:
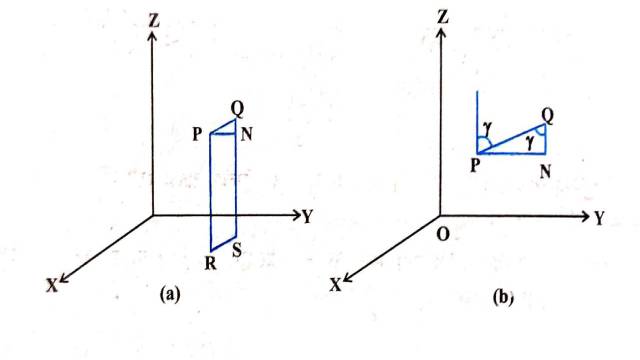
मान लीजिए कि रेखा PQ की दिक्-कोसाइन l,m,n हैं और x,y और z-अक्ष के साथ कोण क्रमशः \alpha,\beta, \gamma बनाती हैं।
मान लीजिए P और Q से लम्ब खींचिए जो XY-तल को R तथा S पर मिलते हैं।P से एक अन्य लम्ब खींचिए जो QS को N पर मिलता है। अब समकोण त्रिभुज PNQ में, \angle PQN= \gamma \\ \cos \gamma=\frac{N Q}{P Q}= \frac{z_2-z_1}{PQ}
इसी प्रकार \cos \beta=\frac{y_2-y_1}{P Q} और \cos \alpha=\frac{x_2-x_1}{PQ}
अतः बिन्दुओं P(x_1,y_1,z_1) तथा Q(x_2,y_2,z_2) को जोड़ने वाले रेखाखण्ड PQ की दिक्-कोसाइन
\frac{x_2-x_1}{PQ}, \frac{y_2-y_1}{PQ}, \frac{z_2-z_1}{PQ} हैं।
जहाँ PQ=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}
5.रेखा के दिक्-कोसाइन कक्षा 12 (Frequently Asked Questions Related to Direction Cosines Class 12),कक्षा 12 में रेखा के दिक्-कोसाइन (Direction Cosines in Class 12) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.रेखा की दिक्-कोसाइन किसे कहते हैं? (What is the Direction Cosines of the Line?):
उत्तरःरेखा L द्वारा x,y और z-अक्षों के साथ क्रमशः \alpha, \beta और \gamma बनाए गए कोण दिक्-कोण कहलाते हैं तब इन कोणों की कोसाइन नामतः \cos \alpha, \cos \beta और \cos \gamma रेखा L के दिक्-कोसाइन (direction cosines or dc’s) कहलाती हैं।
प्रश्न:2.मूल बिन्दु से नहीं गुजरने वाली रेखा के दिक्-कोसाइन कैसे ज्ञात करते हैं? (How is the Direction Cosines of a Line Not Passing Through the Origin Determined?):
उत्तर:अन्तरिक्ष में दी गई रेखा यदि मूल बिन्दु से नहीं गुजरती है तो इसकी दिक्-कोसाइन को ज्ञात करने के लिए,हम मूल बिन्दु से दी गई रेखा के समान्तर एक रेखा खींचते हैं।अब मूल बिन्दु से इनमें से एक सदिश रेखा के दिक्-अनुपात ज्ञात करते हैं क्योंकि दो समान्तर रेखाओं के दिक्-अनुपातों के समूह समान(वही) होते हैं।
प्रश्न:3.दिक्-अनुपात किसे कहते हैं? (What is the Direction Ratios?):
उत्तर:एक रेखा के दिक्-कोसाइन के समानुपाती संख्याओं को रेखा के दिक्-अनुपात (direction ratios or dr’s) कहते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा रेखा के दिक्-कोसाइन कक्षा 12 (Direction Cosines Class 12),कक्षा 12 में रेखा के दिक्-कोसाइन (Direction Cosines in Class 12) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here | |
| 7. | click here |
Direction Cosines Class 12
रेखा के दिक्-कोसाइन कक्षा 12
(Direction Cosines Class 12)
Direction Cosines Class 12
रेखा के दिक्-कोसाइन कक्षा 12 (Direction Cosines Class 12) के इस आर्टिकल में रेखाओं
के दिक्-कोसाइन ज्ञात करने के लिए सवालों को हल करके समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.