Complex Number in Complex Analysis
1.सम्मिश्र विश्लेषण में सम्मिश्र संख्याएँ (Complex Number in Complex Analysis),सम्मिश्र संख्याएँ (Complex Numbers):
सम्मिश्र विश्लेषण में सम्मिश्र संख्याएँ (Complex Number in Complex Analysis) के इस आर्टिकल में वर्ग के शीर्ष,बिन्दुओं के प्रतिबिम्ब,सम्मिश्र तल में वृत्त,गोले का समीकरण ज्ञात करने के बारे में अध्ययन करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Contour Integration in ComplexAnalysis
2.सम्मिश्र विश्लेषण में सम्मिश्र संख्याएँ के उदाहरण (Complex Number in Complex Analysis Illustration):
Illustration:12.z का बिन्दुपथ ज्ञात कीजिए जबकि
(Find the locus of z,when)
Illustration:12(ii). \left|\frac{z-i}{z+i}\right| \geq 2
Solution: \left|\frac{z-i}{z+i}\right| \geq 2 \\ \Rightarrow \frac{|z-i|}{|z+i|} \geq 2 \\ \Rightarrow|z-i| \geq 2|z+i| \\ \Rightarrow|x+i y-i| \geq 2|x+i y+i| \\ \Rightarrow|x+i(y-1)| \geq 2|x+i(y+1)| \\ \Rightarrow \sqrt{x^2+(y-1)^2} \geq 2 \sqrt{x^2+(y+1)^2} \\ \Rightarrow x^2+(y-1)^2 \geq 4\left(x^2+(z+1)^2\right) \\ \Rightarrow x^2+y^2-2 y+1 \geq 4\left(x^2+y^2+2 y+1\right) \\ \Rightarrow x^2+y^2-2 y+1 \geq 4 x^2+4 y^2+8 y+y \\ \Rightarrow 3 x^2+3 y^2+10 y+3 \leq 0
अतः बिन्दुपथ
वृत्त 3 x^2+3 y^2+10 y+3=0 के ऊपर एवं अन्दर स्थित सभी बिन्दुओं का क्षेत्र
Illustration:12(iii). \left|z^2-1\right|<2
Solution: \left|z^2-1\right|<2 \\ \Rightarrow\left|z^2-1\right|^2<4 \\ \Rightarrow\left(z^2-1\right) \left(\bar{z}^2-1\right)<4 \\ \Rightarrow z^2 \bar{z}^{2}-\left(z^2+\bar{z}^2\right)+1<4 \\ \Rightarrow \left(x^2+y^2\right)^2-2\left(x^2-y^2\right)-3<0 \\ \Rightarrow r^4-2 r^2 \cos 2 \theta-3<0
वक्र r^4-2 r^2 \cos 2 \theta-3=0 के अन्दर का क्षेत्र
Illustration:13.प्रदर्शित कीजिए (Show that)
\left|a+\sqrt{\left(a^2-b^2\right)}\right|+\left|a-\sqrt{\left(a^2-b^2\right)}\right|=|a+b|+|a-b|
Solution: \left|a+\sqrt{\left(a^2+b^2\right)}\right|+\left|a-\sqrt{\left(a^2-b^2\right)}\right| =|a+b|+|a-b| \\ \left|z_1+z_2\right|^2 =\left(z_1+z_2\right)\left(\overline{z_1+z_2}\right) \\ =\left(z_1+z_2\right) \left(\overline{z_1}+\overline{z_2}\right) \\ \Rightarrow \left|z_1+z_2\right|^2=z_1 \overline{z}_1+z_1 \bar{z}_2+z_2 \overline{z_1}+z_2 \bar{z}_2 \cdots(1)
तथा \left|z_1-z_2\right|^2=\left(z_1-z_2\right)\left(\overline{z_1-z_2}\right) \\ =\left(z_1-z_2\right) \left(\overline{z_1}-\overline{z}_2\right) \\ \Rightarrow\left|z_1-z_2\right|^2=z_1 \bar{z}_1-z_1 \bar{z}_2-z_2 \bar{z}_1+z_2 \overline{z_2} \cdots(2)
(1) व (2) को जोड़ने पर:
\left|z_1+z_2\right|^2+\left|z_1-z_2\right|^2=2 z_1 \bar{z}_1+2 z_2 \bar{z}_2 \\ \Rightarrow \left|z_1+z_2\right|^2+\left|z_1-z_2\right|^2=2\left|z_1\right|^2+2\left|z_2\right|^2 \cdots(3)\\ \Rightarrow\left|z_1\right|^2+\left|z_2\right|^2=\frac{1}{2}\left[\left|z_1+z_2\right|^2+\left|z_1-z_2\right|^2\right] \cdots(4)
माना z_1=a+\sqrt{a^2-b^2} तथा z_2=a-\sqrt{a^2-b^2} \\ z_1+z_2=2 a
तथा z_1-z_2=2 \sqrt{a^2-b^2}
समीकरण (4) में मान रखने पर:
\left|z_1\right|^2+\left|z_2\right|^2=\frac{1}{2}\left[|2 a|^2+\left|2 \sqrt{a^2-b^2}\right|^2\right] \\ \Rightarrow \left|z_1\right|^2+ \left|z_2\right|^2=2|a|^2+\left|a^2-b^2\right|
पुनः \left[\left|z_1\right|+\left|z_2\right|\right]^2=|z_1|^2+|z_2|^2+2 |z_1||z_2| \\ =2\left[|a|^2+ \left|a^2-b^2\right|\right]+2\left|a^2-a^2+b^2\right| \\ \Rightarrow \left[\left|z_1\right| +\left|z_2 \right|\right]^2 =2|a|^2+2|b|^2+2\left|a^2-b^2\right|
समीकरण (3) में z_1=a व z_2=b रखने पर:
2|a|^2+2|b|^2= |a+b|^2+|a-b|^2 \cdots(6)
समीकरण (5) व (6) से:
\left[\left|z_1\right|+\left|z_2\right|\right]^2 =|a+b|^2+|a-b|^2+2\left|a^2-b^2\right| \\ =|a+b|^2+|a-b|^2+2|a-b||a+b| \\ =\left[|a+b|+|a-b|\right]^2 \\ \Rightarrow \left|z_1\right| +\left|z_2\right|=|a+b|+|a-b| \\ \Rightarrow \left|a+\sqrt{a^2+b^2}\right|+\left|a-\sqrt{a^2-b^2}\right|=|a+b|+|a-b|
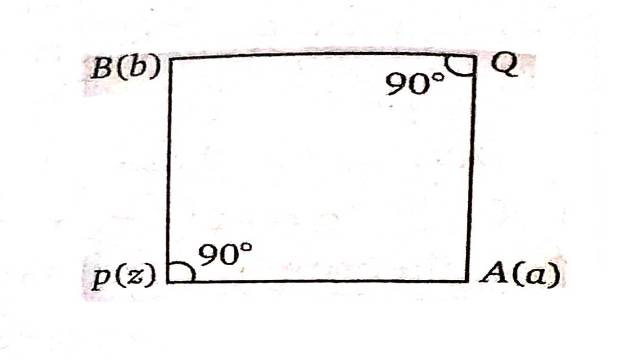
Illustration:14.यदि a एवं b सम्मिश्र संख्याएँ है,तो संख्याएँ z_1 एवं z_2 प्राप्त करिए ताकि z_1,z_2 एवं a,b एक वर्ग के सम्मुख शीर्ष हो।
(If a and b are complex numbers z_1,z_2 ,find numbers so that the points z_1,z_2 and a,b the opposite vertices of a square.)
Solution:माना वर्ग के P व Q तथा A व B सम्मुख शीर्ष हैं।
AP \perp BP \\ \operatorname{amp} \frac{z-a}{z-b}=\frac{\pi}{2}
अतः \frac{z-a}{z-b} शुद्ध काल्पनिक है तथा इसका वास्तविक भाग शून्य है।
परन्तु \operatorname{Re}(z)=\frac{1}{2}(z+\bar{z}) \\ \therefore \frac{1}{2}\left[\frac{z-a}{z-b}+ \frac{\bar{z}-\bar{a}}{\bar{z}-\bar{b}}\right]=0 \\ \Rightarrow \frac{z-a}{z-b}+\frac{\bar{z}-\bar{a}}{\bar{z}-\bar{b}}=0 \cdots(1)
पुनः PAQB एक वर्ग है अतः AP=BP
|z-a|=|z-b| \\ \Rightarrow |z-a|^2=|z-b|^2 \\ \Rightarrow (z-a)(\bar{z}-\bar{a})=(z-b)(\bar{z}-\bar{b}) \\ \Rightarrow \frac{z-a}{z-b}=\frac{\bar{z}-\bar{b}}{\bar{z}-\bar{a}} \cdots(2)
(1) व (2) से:
\frac{z-a}{z-b}+\frac{z-b}{z-a}=0 \\ \Rightarrow (z-a)^2+(z-b)^2=0 \\ \Rightarrow 2 z^2-2 z(a+b)+\left(a^2+b^2\right)=0 \\ \Rightarrow z=\frac{2(a+b) \pm \sqrt{4(a+b)^2-8\left(a^2+b^2\right)}}{4} \\ \Rightarrow z=\frac{1}{2}(a+b) \pm i(a-b)
अतः z_1=\frac{1}{2}(a+b)+i(a-b)
तथा z_2=\frac{1}{2}(a+b)-i(a-b)
Illustration:15.इकाई त्रिज्या के रीमान गोले पर स्थित बिन्दु (\xi, \eta, \zeta) का सम्मिश्र आर्गेण्ड-तल पर संगत बिन्दु ज्ञात कीजिए।
(Given a point (\xi, \eta, \zeta) on the Riemann sphere of the unit radius,find its corresponding point on the complex argand plane.)
या
Illustration:20. R^3 में गोले x^2+y^2+z^2=1 पर स्थित बिन्दुओं के विस्तारित सम्मिश्र समतल z=x+iy में त्रिविम प्रक्षेप ज्ञात कीजिए।यह भी प्रदर्शित करिए कि इस प्रक्षेप के अन्तर्गत बिन्दु z=x+iy का गोले पर संगत बिन्दु
\left(\frac{2 x}{x^2+y^2+1}, \frac{2 y}{x^2+y^2+1}, \frac{x^2+y^2-1}{x^2+y^2+1}\right) है
निम्न गोले पर संगति क्या है?
(i)z-समतल में रेखाएँ
(ii)z-समतल में वृत्त जिनके केन्द्र मूलबिन्दु है।
(Describe the stereographic projection of points on the unit sphere in to the extended complex plane,z=x+iy show that under this projection, the point z=x+iy corresponds to the point
\left(\frac{2 x}{x^2+y^2+1}, \frac{2 y}{x^2+y^2+1}, \frac{x^2+y^2-1}{x^2+y^2+1}\right)
on the sphere.What corresponds on the sphere to (i)straight lines in the z-plane, (ii)circles in the z-plane with origin as centre.)
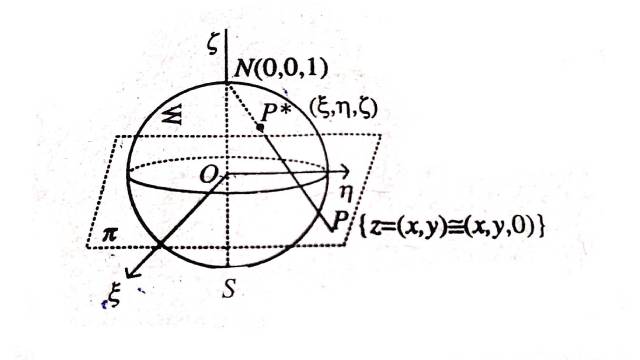
Solution:एक \Sigma गोला जिसकी त्रिज्या इकाई तथा केन्द्र O एवं आर्गेण्ड समतल \pi में बिन्दु P(x,y) से निरूपित कर सकते हैं।गोले के बिन्दुओं को समतल के बिन्दुओं से सम्बद्ध करने के लिए सर्वप्रथम गोले के व्यास NOS की रचना करते हैं जो समतल \pi के लम्बवत है।बिन्दु N तथा S को क्रमशः उत्तरी तथा दक्षिणी ध्रुव कहते हैं।अब हम एक रेखाखण्ड की रचना करते हैं जो N एवं S समतल \pi पर बिन्दु P को मिलाता है तब रेखाखण्ड NP या NP को बढ़ाने पर गोले \Sigma को N के अतिरिक्त एक अन्य अद्वितीय बिन्दु पर काटता है इस बिन्दु को P* मान लेते हैं।स्पष्ट है इस प्रकार की रचना गोले \Sigma के समस्त (N के अतिरिक्त) तथा समतल \pi के सभी बिन्दुओं के मध्य ऐकिक प्रतिचित्रण प्रदान करता है।इस रचना को त्रिविम प्रक्षेप कहते हैं।यदि समतल \pi पर P सम्मिश्र संख्या z को निरुपित करता है तो बिन्दु P* सम्मिश्र संख्या z को रीमान गोले पर निरूपित करेगा।इस प्रतिचित्रण के अन्तर्गत विस्तारित सम्मिश्र समतल (Extended complex plane) में अनन्त बिन्दु गोले पर बिन्दु N के समवर्ती होगा।
विश्लेषणात्मक रूप में इस प्रतिचित्रण को निम्न प्रकार से व्यक्त करते हैं:
माना कि गोले \Sigma का समीकरण
\xi^2+\eta^2+\zeta^2=1 \cdots(1)
तथा प्रक्षेप समतल का समीकरण
\zeta=0 \cdots(2) है।
स्पष्ट है कि N के निर्देशांक (0,0,1) होंगे |
माना कि गोले \Sigma बिन्दु P* के निर्देशांक (\xi, \eta, \zeta) तथा समतल \pi पर संगत बिन्दु P के निर्देशांक (x,y,0) हैं,जहाँ रेखा NP* प्रक्षेप समतल को मिलती है।
चूँकि बिन्दु (0,0,1),(\xi, \eta, \zeta),(x,y,0) एक सरल रेखा में है।अतः
\frac{\xi-0}{x-0}=\frac{\eta-0}{y-0}=\frac{\zeta-1}{0-1}=k या \frac{\xi}{x}=\frac{\eta}{y}=\frac{\zeta-1}{-1}=k \cdots(3)
जहाँ k एक वास्तविक संख्या है।परन्तु बिन्दु (\xi, \eta, \zeta) इकाई गोले \Sigma पर स्थित है जिसका समीकरण (1) है।अतः
x^2 k^2+y^2 k^2+(1-k)^2=1 \\ \Rightarrow k=\frac{2}{x^2+y^2+1} \quad(\because k \neq 0)
समीकरण (1) से समतल \pi पर स्थित सम्मिश्र संख्या (x,y,0) के संगत गोले \Sigma पर स्थित समवर्ती बिन्दु (\xi, \eta, \zeta) के निर्देशांक होंगे
\left(\frac{2 x}{x^2+y^2+1}, \frac{2 y}{x^2+y^2+1}, \frac{x^2+y^2-1}{x^2+y^2+1}\right) \cdots(4)
पुनः z=x+iy लेने पर इस सम्मिश्र संख्या के संगत गोले पर बिन्दु
(\xi, \eta, \zeta)=\left(\frac{z+\bar{z}}{|z|^2+1}, \frac{z-\bar{z}}{|z|^2+1} ,\frac{|z|^2-1}{|z|^2+1}\right) \cdots(5)
के समवर्ती होगा।साथ ही (3) से
x=\frac{\xi}{1-\zeta}, y=\frac{\eta}{1-\zeta} ,z=\frac{\zeta+i \eta}{1-\zeta}
समीकरण (5) एवं (6) सम्मिश्र संख्याओं तथा गोले पर बिन्दुओं के मध्य ऐकिक संगतता स्थापित करता है केवल गोले के शीर्ष बिन्दु N(0,0,1) के समवर्ती सम्मिश्र समतल पर कोई बिन्दु नहीं है।इस बिन्दु N(0,0,1) के संगत बिन्दु सम्मिश्र समतल पर अनन्त पर कोई बिन्दु परिभाषित करते हैं।
Illustration:16.रीमान गोले पर बिन्दु 1,-1, i, \frac{1-i}{\sqrt{2}} के प्रतिबिम्ब बिन्दु ज्ञात कीजिए।
(On the Riemann sphere what are the points 1,-1, i, \frac{1-i}{\sqrt{2}} .)
Solution:1 का प्रतिबिम्ब (1,0,0)
-1 का प्रतिबिम्ब (-1,0,0)
i का प्रतिबिम्ब (0,1,0)
\frac{1-i}{\sqrt{2}} का प्रतिबिम्ब \left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}, 0\right)
Illustration:17.प्रदर्शित करिए कि गोले पर वृत्त जो उत्तर ध्रुव से गुजरते हैं के संगति सम्मिश्र तल में एक सरल रेखा है।
(Show that circle on the sphere passing through the north pole corresponds to a straight line in the complex plane.)
Solution:रीमान गोले पर कोई वृत्त निम्न इकाई गोले तथा एक समतल प्रतिच्छेद है।
\xi^2+\eta^2+\zeta^2=1 \cdots(1)
तथा a \xi+b \eta+c \zeta+d=0 \cdots(2)
प्रक्षेप के शीर्ष N को (0,0,1) मान लिया।माना कि (1) पर किसी बिन्दु P* के निर्देशांक (\xi, \eta, \zeta) हैं तथा इस बिन्दु के समवर्ती बिन्दु P के निर्देशांक (x,y,0) हैं जहाँ रेखा NP* प्रक्षेप समतल (\zeta=0) को काटती है।
अब चूँकि बिन्दु (0,0,1), (\xi, \eta, \zeta) तथा (x,y,0) एक सरल रेखा में हैं इसलिए
\frac{\xi-0}{x-0}=\frac{\eta-0}{y-0}=\frac{\zeta-1}{0-1}=k \\ \frac{\xi}{x}=\frac{\eta}{y}=\frac{\zeta-1}{-1}=k \cdots(3)
जहाँ k एक वास्तविक संख्या है।परन्तु बिन्दु (\xi, \eta, \zeta) (1) एवं (2) पर विद्यमान है।
अतः x^2 k^2+y^2 k^2+(1-k)^2=1 \cdots(4)
तथा k(a x+b y)+c(1-k)+d=0 \cdots(5)
(4) एवं (5) में से k का विलोपन करने पर:
(c+d)\left(x^2+y^2\right)+2 ax+2 b y+d-c=0 \cdots(6)
यदि c+d \neq 0 हो तो (6) एक वृत्त को निरूपित करती है जबकि c+d=0 होने पर यह सरल रेखा को निरूपित करेगी।
परन्तु c+d=0 होगा जबकि समतल (2) N(0,0,1) से गुजरता है।इसलिए यदि गोले पर वृत्त (1) एवं (2) उत्तरी ध्रुव N से गुजरता हो तो इसका प्रक्षेप समतल \pi पर सरल रेखा होगी अन्यथा एक वृत्त होगा।विशेषतः यदि समतल (2) समतल \pi के समान्तर हो तो a=b=0 तब संगत वृत्त (6) का समीकरण
(c+d)\left(x^2+y^2\right)=c-d
होगा जिसका केन्द्र मूलबिन्दु है।
दूसरी ओर यदि तल (2) अक्ष NS से गुजरता हो तो c=d=0 और प्रक्षेप समतल (6) में सरल रेखा
ax+by=0
प्राप्त होगी जो कि मूलबिन्दु से गुजरती है।
Illustration:22.सम्मिश्र तल में दो बिन्दुओं z_1 एवं z_2 को मिलाने वाली सरल रेखा का समीकरण लिखिए।
(Write the equation of an straight line joining two points z_1 and z_2 of a complex plane.)
Solution:माना कि z_1,z_2 आर्गेण्ड समतल पर स्थित बिन्दुओं P,Q के निर्देशांक हैं।माना कि रेखा PQ पर A(z) कोई बिन्दु है तब
\arg \frac{z_1-z_1}{z_1-z_2}=0 या \pi
इसलिए \frac{z-z_1}{z_1-z_2} पूर्णतः वास्तविक राशि है।
अर्थात् \operatorname{Im} \frac{z-z_1}{z_1-z_2}=0 \\ \Rightarrow \frac{z-z_1}{z_1-z_2}-\frac{\overline{z}-\overline{z_1}}{\overline{z_1}-\overline{z_2}}=0 \\ \Rightarrow z\left(\bar{z}_1-\bar{z}_2\right)-\bar{z}\left(z_1-z_2\right)+\left(z_1 \bar{z}_2-\bar{z}_1 z_2\right)=0
उपर्युक्त उदाहरणों के द्वारा सम्मिश्र विश्लेषण में सम्मिश्र संख्याएँ (Complex Number in Complex Analysis),सम्मिश्र संख्याएँ (Complex Numbers) को समझ सकते हैं।
3.सम्मिश्र विश्लेषण में सम्मिश्र संख्याएँ के सवाल (Complex Number in Complex Analysis Questiins):
z का बिन्दुपथ ज्ञात कीजिए जबकि
(Find the locus of z, when)
(1.) \left|\frac{z-1}{z+1}\right|=\lambda
(2.) |z-1|+|z+1| \leq 4
उत्तर (Answers): (1.) x^2+y^2+2 gx+1=0
(2.) \frac{x^2}{4}+\frac{y^2}{3}=1 दीर्घवृत्त के ऊपर तथा अन्दर का क्षेत्र
उपर्युक्त सवालों को हल करने पर सम्मिश्र विश्लेषण में सम्मिश्र संख्याएँ (Complex Number in Complex Analysis),सम्मिश्र संख्याएँ (Complex Numbers) को ठीक से समझ सकते हैं।
Also Read This Article:- Complex Numbers in Complex Analysis
4.सम्मिश्र विश्लेषण में सम्मिश्र संख्याएँ (Frequently Asked Questions Related to Complex Number in Complex Analysis),सम्मिश्र संख्याएँ (Complex Numbers) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.सम्मिश्र संख्याओं के गुणधर्मों को लिखिए। (Write the Properties of Complex Numbers):
उत्तर:(1.)सम्मिश्र संख्या के गुणधर्म
(i) z+\bar{z}=2 \operatorname{Re}(z)
(ii) z-\bar{z}=2 i \operatorname{Im}(z)
(iii) \overline{z_1+z_2}=\overline{z_1}+\overline{z_2}
(iv) \overline{(\bar{z})}=z
(v) \overline{z_1-z_z}=\overline{z_1}-\overline{z_2}
(vi) \overline{z_1 \cdot z_2}=\overline{z_1} \cdot \overline{z}_2
(vii) \overline{\left(\frac{z_1}{z_2}\right)}=\frac{\bar{z}_1}{\overline{z_2}}, z_2 \neq 0
(viii) z \overline{z}=[\operatorname{Re}(z)]^2+[\operatorname{Im}(z)]]^2
(2.)सम्मिश्र संख्या के मापांक के गुणधर्म
(i)|z| \geq \mid \operatorname{Re} z)|\geq \operatorname{Re}(z) ;| z|\geq | \operatorname{Im}(z) | \geq \operatorname{Im}(z)
(ii)|z|=|\bar{z}|
(iii) z \bar{z}=|z|^2
(iv)\left|z_1 z_2\right|=|z_1||z_2|
(v)\left|\frac{z_1}{z_2}\right|=\frac{\left|z_1\right|}{\left|z_2\right|},\left|z_2\right| \neq 0
(vi) \left|z_1+z_2\right| \leq\left|z_1\right|+\left|z_2\right|
(vii) \left|z_1-z_2\right| \geq \left|z_1\right|-\left|z_2\right|
(viii)\left|z_1-z_2\right| \leq \left|z_1\right|+\left|z_2\right|
(ix)\left|z_1+z_2\right| \geq \left|z_1\right|-\left|z_2\right|
प्रश्न:2.दो सम्मिश्र संख्याओं के संपाती होने पर टिप्पणी लिखो। (Write a Note on the Collinear of Two Complex Numbers):
उत्तर:यदि दो सम्मिश्र रेखाएँ सम्पाती हों तो
\arg \left(\frac{z_2-z_0}{z_1-z_0}\right)=0 \text { या } \pi
अतः \frac{z_2-z_0}{z_1-z_0} वास्तविक है।फलतः यदि \frac{\left(z_2-z_0\right)}{\left(z_1-z_0\right)} वास्तविक है तो सम्मिश्र संख्या के बिन्दु समरेख (collinear) होंगे।
प्रश्न:3.दो सम्मिश्र रेखाओं के लम्बवत होने पर टिप्पणी लिखो। (Write a Note on the Perpendicular of Two Complex Lines):
उत्तर:यदि दो सम्मिश्र रेखाएँ लम्बवत हो,तो
\arg \frac{\left(z_2-z_0\right)}{z_1-z_0}= \pm \frac{\pi}{2}
अतः \frac{z_2-z_0}{z_1-z_0} विशुद्ध काल्पनिक होगी।
उपर्युक्त प्रश्नों के उत्तर द्वारा सम्मिश्र विश्लेषण में सम्मिश्र संख्याएँ (Complex Number in Complex Analysis),सम्मिश्र संख्याएँ (Complex Numbers) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Complex Number in Complex Analysis
सम्मिश्र विश्लेषण में सम्मिश्र संख्याएँ
(Complex Number in Complex Analysis)
Complex Number in Complex Analysis
सम्मिश्र विश्लेषण में सम्मिश्र संख्याएँ (Complex Number in Complex Analysis) के इस
आर्टिकल में वर्ग के शीर्ष,बिन्दुओं के प्रतिबिम्ब,सम्मिश्र तल में वृत्त,गोले का समीकरण ज्ञात
करने के बारे में अध्ययन करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.