Roots of Equation in Complex Analysis
1.सम्मिश्र विश्लेषण में समीकरण के मूल (Roots of Equation in Complex Analysis),सम्मिश्र विश्लेषण में समीकरण के मूल ज्ञात करना (To Find Roots of Equation in Complex Analysis):
सम्मिश्र विश्लेषण में समीकरण के मूल (Roots of Equation in Complex Analysis) के इस आर्टिकल में समीकरण के मूल ज्ञात करने से सम्बन्धित सवालों को हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Illustrations of Kind of Singularities
2.सम्मिश्र विश्लेषण में समीकरण के मूल के साधित उदाहरण (Roots of Equation in Complex Analysis Solved Illustrations):
Illustration:1.रुशे के प्रमेय का उपयोग करके बहुपद P(z)=z^{10}-6 z^7+3 z^3+1,|z| < 1 के अन्दर स्थित शून्यों की संख्या ज्ञात कीजिए।
(Using Rouche’s theorem determine the number of zeros of the polynomial P(z)=z^{10}-6 z^7+3 z^3+1 in |z| < 1 )
Solution:यहाँ P(z)=z^{10}-6 z^7+3 z^3+1
माना f(z)=-6 z^7, g(z)=z^{10}+3 z^3+1
तब P(z)=f(z)+g(z)
रूश के प्रमेय को लागू करने पर,हम पाते हैं कि
f(g)+g(z)=P(z) में C के अंदर शून्यों की संख्या f(z)=-6 z^{7} के समान है।लेकिन C के अंदर f(z) के सात शून्य हैं।अतः C के अंदर P(z) के सात शून्य हैं।
Illustration:2.दर्शाइए कि समीकरण f(z)=z^4+4(1+i) z+1 का प्रत्येक चतुर्थांश में एक मूल है।
(Show that the equation f(z)=z^4+4(1+i) z+1 has one root in each quadrant.)
Solution: f(z)=f(z)=z^4+4(1+i) z+1
चूँकि f(z) एक बहुपद है,इसलिए यह z के सभी परिमित मानों के लिए विश्लेषिक है,परिणामस्वरूप यह वृत्ताकार डिस्क के सभी चार चतुर्थांशों में विश्लेषिक है, जिसका केंद्र मूल बिंदु पर है और त्रिज्या R के बराबर है जहाँ R बड़ा है।
मान लीजिए कि C डिस्क के पहले चतुर्थांश की पूर्ण सीमा है।फिर C एक बंद वक्र है जिसमें वृत्त |z|=R का पहला चौथाई arc AB होता है और दो त्रिज्याएँ OA और OB इसके सिरों को मूल बिन्दु O से जोड़ते हैं।
अब,विचार करें:
(1.)वास्तविक अक्ष का भाग OA।
वास्तविक अक्ष पर z=x और x,0 से \infty तक चलता है (क्योंकि R बड़ा है)।
f(z)=x^4+4 (1+i)x+4 i x \\ =\left(x^4+4x+1\right)+4 i x
इसलिए \arg f(z)=\tan^{-1} \left(\frac{4 x}{x^4+4x+1}\right) ,OA पर arg f(z) के लिए
\therefore \Delta OA \arg f(z)=\left[\tan^{-1} \frac{4 x}{x^4+4 x+1}\right]_0^{\infty}=0 \cdots(1)
(2.)प्रथम चतुर्थांश में arc AB।
इस चाप पर z=R e^{i \theta} तथा \theta , 0 से \frac{\pi}{2} तक चलता है।
f(z)=z^4+4(1+i) z+1 \\ =R^4 e^{4 i \theta}+4(1+i) R e^{j \theta}+1 [arc AB पर किसी z के लिए]
=R^4 e^{4 i \theta}\left[1+\frac{4(1+i)}{R^3 \cdot e^{3 i \theta}}+\frac{1}{R^4 \cdot e^{4 i \theta}} \right] \\ \rightarrow R^4 e^{4 i \theta} \text { as } R \rightarrow \infty
इसलिए \arg f(z)=4 \theta [arc AB पर किसी z के लिए]
\therefore \triangle AB \arg f(z)=\left[4 \theta\right]_0^{\frac{\pi}{2}}=4 \cdot \frac{1}{2} \pi=2 \pi \cdots(2)
(3.)भाग BO का काल्पनिक अक्ष
काल्पनिक अक्ष पर z=iy तथा y \infty से 0 तक चलता है
f(z)=(i y)^4+4(1+i) i y+1, OB पर
=\left(y^4-4 y+1\right)+4 i y
इसलिए \arg f(z)=\tan ^{-1}\left(\frac{4 y}{y-4 y+1}\right), BO पर किसी z के लिए
\therefore \triangle BO \cdot \arg f(z)=\left[\tan ^{-1}\left(\frac{4 y}{y^2-4 y+1}\right)\right]_{\infty}^0=0 \cdots(3)
फ़ंक्शन f(z) के विश्लेषिक की शर्त बंद वक्र C के भीतर और उस पर संतुष्ट होने के कारण,हमारे पास कोणांक सिद्धांत द्वारा,C के भीतर f(z) के शून्यों की संख्या है।
=\frac{1}{2 \pi} \Delta C \arg f(z) \\ =\frac{1}{2 \pi}[\Delta O A \arg f(z)+\Delta A B \arg f(z)+\Delta B O \arg f(z)] \\ =\frac{1}{2 \pi}[0+2 \pi+0] [(1),(2) तथा (3)से]
=1
यह प्रदान करते हुए कि दिए गए समीकरण का एक मूल पहले चतुर्थांश में है।
चूँकि चारों मूल सम्मिश्र हैं और चूंकि सम्मिश्र मूल युग्म में मौजूद हैं,इसलिए एक मूल (पहले वाले का संयुग्मी) चौथे चतुर्थांश में स्थित होना चाहिए।लेकिन चूंकि समीकरण चार घात का है,इसलिए संयुग्मी मूलों की अन्य युग्म दूसरे और तीसरे चतुर्थांश में से प्रत्येक में एक है।
इसलिए दिए गए समीकरण में प्रत्येक चतुर्थांश में एक मूल है।
Illustration:3.कौनसे चतुर्थांश में समीकरण z^4+4 z^3+8 z^2+8 z+4=0 के मूल स्थित हैं?
(In which quadrant do the roots of the equation z^4+4 z^3+8 z^2+8 z+4=0 lie?)
Solution:z-समतल के चार चतुर्थांशों को वृत्त के चार चतुर्थांशों के रूप में माना जा सकता है जहाँ R बड़ा है।
इस वृत्त के पहले चतुर्थांश पर विचार करें।इसमें त्रिज्या OA,वृत्त का एक चौथाई arc AB और त्रिज्या BO (एंटी-क्लॉक चलती हुई) होता है जहाँ A,B की ओर जाता है।
चूंकि फ़ंक्शन f(z)=z^4+4 z^3+8 z^2+8 z+4, z में एक बहुपद है,इसलिए यह पहले चतुर्थांश की सीमा के भीतर और उस पर विश्लेषिक है।
(i)सीमा OA वास्तविक अक्ष है।
तो OA पर,z=x, जहाँ x,0 से तक जाता है
तथा f(x)=x^4+4 x^3+8 x^2+8 x+4 और OA पर प्रत्येक x के लिए अशून्य है।
\therefore \arg f(z)=\tan ^{-1}\left(\frac{0}{x^4+4 x^3+8 x^2+8 x+4}\right) ,OA पर प्रत्येक x के लिए
\therefore \triangle O A \arg f(z)=0
(ii)arc AB पर, z=R e^{i \theta} तथा \theta ,0 से \frac{\pi}{2} तक जाता है
तथा f(z)=z^4+4 z^3+8 z^2+8 z+4 \\ =R^4 e^{4 i \theta}+4 R^3 e^{3 i \theta}+8 R^2 e^{2 i \theta}+8 R e^{i \theta}+4 \\ =R^4 \cdot e^{4 i \theta}\left[1+\frac{4}{R e^{i \theta}}+\frac{8}{R^2 e^{2 i \theta}}+\frac{8}{R^3 e^{3 i \theta}}+\frac{4}{R^4 e^{4 i \theta}}\right] \\ \rightarrow R^4 e^{4 i \theta} \text { as } R \rightarrow \infty
अतः \arg f(z)=4 \theta, arc AB पर z के लिए
\therefore \triangle_{\text{arc AB}} \arg f(z)=[4 \theta]_0^{\frac{\pi}{2}}=2 \pi
(iii) सीमा BO काल्पनिक अक्ष है,इस पर z=iy जहाँ y \infty से 0 की ओर गति करता है।
f(z)=(i y)^4+4(i y)^3+8(i y)^3 +8(i y)+4 \\ =\left(y^2-8 y^2+4\right)+i\left(8 y-4 y^3\right), जो कि अशून्य है
इसलिए \arg f(z)=\tan^{-1} \left(\frac{8 y-4 y^3}{y^4-8 y^2+4}\right) \\ \therefore \Delta_{B O} \arg f(z)=\left[\frac{\tan^{-1} 4 y\left(2-y^2\right)}{y^4-8 y^2+4}\right]_{\infty}^0,
जो कि दोनों सीमाओं के लिए शून्य है।
इसका तात्पर्य है कि बिन्दु w=f(z) वास्तविक अक्ष के किसी बिन्दु से आरम्भ होते हुए इस अक्ष पर कुछ बिन्दुओं के लिए वापस आता है।इस तरीके से निम्न प्रकार से स्थान लेता है:
\frac{4 y\left(2-y^2\right)}{y^4-8 y^2+4} का चिन्ह पर=\begin{array}{|c|c} 0, y=\infty \text { पर } & 0 \\ - \text { के लिए } \sqrt{2} < y < \infty & \text{चतुर्थ चतुर्थांश में रहता है}\\ 0, y=2 \text { पर } & 0 \\ + \text { के लिए } 0 < y < \sqrt{2} & \text{प्रथम चतुर्थांश में रहता है} \\ 0, y=0 \text { पर } & 0 \end{array}
इसका अर्थ है कि y, \infty से 0 तक जाता है,w वास्तविक अक्ष पर कुछ बिन्दुओं के लिए वास्तविक अक्ष पर लौटता है और पुनः प्रथम चतुर्थांश यह बिन्दु पुनः प्रारम्भ होता है और पुनः वास्तविक अक्ष पर कुछ बिन्दुओं पर लौटता है।इस प्रकार arg f(z) का विचलन शून्य है जैसे y, \infty से 0 तक जाता जिसे इस प्रकार लिखा जाता है:
\Delta BO \arg f(z)=0
अतः कोणांक सिद्धान्त द्वारा पहले चतुर्थांश में शून्यों की संख्या है:
N=\frac{1}{2 \pi} \Delta C \arg f(z) \\ =\frac{1}{2 \pi}[\Delta OA f(z)+\Delta arc AB \arg f(z) +\Delta BO \arg f(z)] \\ =\frac{1}{2 \pi}[0+2 \pi+0]=1
यह दिखाता है कि पहले चतुर्थांश में एक शून्य है। समीकरण सभी गुणांक वास्तविक और धनात्मक के साथ 4 घात का है,इसलिए इसकी केवल चार सम्मिश्र मूल होनी चाहिए और इसलिए उन्हें युग्म में जाना चाहिए।
जैसा कि हमने अभी ऊपर दिखाया है,एक मूल पहले चतुर्थांश में स्थित है,इसलिए पहले वाले का एक मूल संयुग्मी चौथे चतुर्थांश में स्थित होना चाहिए।और शेष दो मूल में से एक दूसरे चतुर्थांश में स्थित है और दूसरा संयुग्मी तीसरे चतुर्थांश में स्थित है।इसलिए प्रत्येक चतुर्थांश में एक मूल होता है।
Illustration:4.दर्शाइए कि समीकरण z^3+i z+1=0 का प्रत्येक पहले,द्वितीय तथा चौथे चतुर्थांश में एक-एक मूल है।
(Show that the equation z^3+i z+1=0 has a root in each of the first,second and fourth quadrant.)
Solution:मान लीजिए f(z)=z^3+i z+1=0 ,जैसा कि पिछले दो उदाहरणों में है,हम दिखा सकते हैं कि दिए गए समीकरण की वास्तविक या काल्पनिक अक्ष पर कोई मूल नहीं हो सकती हैं।अब हम पहले चतुर्थांश में सम्मिश्र मूल की खोज करते हैं।हम लिखते हैं
f(z)=u+iv ताकि u=z^3+1 और v=z
(i)x-अक्ष पर,हम लिखते हैं z=x ताकि u=x^3+1 तथा v=x
\therefore \arg f(z)=\tan ^{-1}\left(\frac{x}{x^3+1}\right)
अब \underset{x \rightarrow \infty}{\lim} \left(\frac{x}{x^3+1}\right)=0
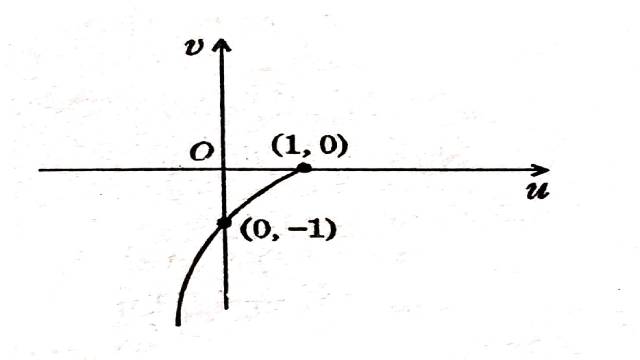
जब 0< x< \infty होता है,तो u और v दोनों धनात्मक होते हैं।अतः जब x=0,u=1 तथा v=0।अतः z,0 से \infty तक x-अक्ष के अनुदिश गति करता है,तो बिंदु (u, v),(1,0) से प्रारंभ होकर और पहले चतुर्थांश में शेष \infty की ओर गति करता है जहाँ वक्र u-अक्ष के समांतर होता है ताकि वास्तविक धनात्मक अक्ष पर z गति के रूप में है तो arg f(z) में कोई परिवर्तन न हो।
(ii) चूँकि समीकरण तृतीय घात का है,इसलिए arg f(z) में परिवर्तन 3 \cdot \frac{\pi}{2}=\frac{3 \pi}{2} है जहाँ z, z=R e^{i \theta}, 0 \leq \theta \leq \frac{\pi}{2} के अनुदिश चलता है,जहाँ R \longrightarrow \infty
(iii)y-अक्ष पर,हम z=iy लिखते हैं
तब f(iy)=-i y^3-y+1=(1-y)-i y^3 \\ \therefore \arg f(i y)=\tan ^{-1}\left(\frac{v}{u}\right)=\tan^{-1} \left(\frac{-y^3}{1-y}\right)
अब \frac{-y^3}{1-y} का अंश 0 है जब y = 0 और इसका हर y = 1 पर गायब हो जाता है।इस प्रकार जब 1 < y < \infty ,u और v दोनों ऋणात्मक हैं। y=1,u=0,v=-1 पर और जब 0<y<1,u धनात्मक और v ऋणात्मक होता है।y=0,u=1 और v=0 पर।अतः y \infty से 0 तक परिवर्तित होता है,तीसरे चतुर्थांश में बिंदु (u,v) \infty से शुरू होता है जहाँ वक्र v-अक्ष के समान्तर होता है,बिंदु (0,-1) पर जाता है और फिर चौथे चतुर्थांश में रहने के बाद बिंदु (1,0) पर आता है। अतः arg f(z) में z के काल्पनिक अक्ष के अनुदिश गति करने पर परिवर्तन \frac{\pi}{2} है।अतः arg f(z) में कुल परिवर्तन है :
0+\frac{3 \pi}{2}+\frac{\pi}{2}=2 \pi
अतः कोणांक सिद्धांत द्वारा प्रथम चतुर्थांश में f(z) के शून्यों की संख्या \frac{1}{2 \pi} \times 2 \pi=1 है।
इसलिए दिए गए समीकरण का पहले चतुर्थांश में एक मूल है।
अब हम दूसरे चतुर्थांश में f(z)=0 के मूल को देखते हैं। जैसा कि ऊपर देखा गया है,काल्पनिक अक्ष के अनुदिश \infty से 0 की ओर बढ़ने पर arg f(z) में परिवर्तन \frac{\pi}{2} है।अतः arg f(z) में परिवर्तन जैसा कि z काल्पनिक अक्ष के अनुदिश 0 से \infty तक चलता है, – \frac{\pi}{2} है।वृत्त के चतुर्थांश के अनुदिश arg f(z) में भी परिवर्तन
z=R e^{i \theta}, \frac{\pi}{2} \leq \theta \leq \pi \\ 3 \times\left(\pi-\frac{\pi}{2}\right)=\frac{3 \pi}{2} है।
अब हम arg f(z) में परिवर्तन ज्ञात करते हैं क्योंकि z वास्तविक अक्ष पर -R से 0 तक चलता है जहाँ R \rightarrow \infty | z=-x रखने पर,हमें प्राप्त होता है
f(-x)=-x^3-i x+1=\left(1-x^3\right)-i x \\ \therefore \arg f(-x)=\tan ^{-1}\left(\frac{u}{v}\right)=\tan ^{-1}\left(\frac{-x}{1-x^3}\right)
अब \underset{x \rightarrow \infty}{\lim} \left(\frac{u}{v}\right)=\underset{x \rightarrow \infty}{\lim} \left(\frac{-x}{1-x^3}\right)=0
इस प्रकार u=1-x^3 तथा v=-x
u=0 जब x=1 और v=0 जब x=0
साथ ही जब 1< x< \infty ,u और v दोनों ऋणात्मक हैं और जब 0<x<1;u धनात्मक है और v ऋणात्मक है।अतः चूँकि x, \infty से 1 तक बदलता है,तीसरे चतुर्थांश में \infty से शुरू होने वाला बिंदु जहाँ वक्र u-अक्ष के समान्तर होता है,और तीसरे चतुर्थांश में शेष बिंदु (0,-1) पर आता है और जब x,1 से 0 तक बदलता है,तो बिंदु (u,v),(0,-1) से शुरू होता है और चौथे चतुर्थांश में शेष बिंदु (1,0) तक पहुँच जाता है।यह इस प्रकार अनुकरण करता है कि arg f(z) में परिवर्तन है चूँकि z,ऋणात्मक वास्तविक अक्ष के अनुदिश \infty से 0 तक चलता है।अतः arg f(z) में कुल परिवर्तन है
-\frac{\pi}{2}+3 \frac{\pi}{2}+\pi=2 \pi
इसलिए कोणांक सिद्धांत द्वारा,दूसरे चतुर्थांश में f(z) के शून्य की संख्या है:
\frac{1}{2 \pi} \times 2 \pi=1
इस प्रकार दिए गए समीकरण का एक मूल दूसरे चतुर्थांश में है।
हमारे इसे सत्यापित करने के लिए पाठक पर छोड़ते है कि दिए गए समीकरण का चौथे चतुर्थांश में एक मूल है।
Illustration:5.दर्शाइए कि समीकरण z^4+2 z^3+3 z^2+4 z+5=0 का कोई वास्तविक या विशुद्ध काल्पनिक मूल नहीं है और प्रत्येक चतुर्थांश में इसका एक सम्मिश्र मूल है।
(Show that the equation z^4+2 z^3+3 z^2+4 z+5=0 has no real or purely imaginary roots and that it has one complex root in each quadrant.)
Solution:मानलो f(z)=z^4+2 z^3+3 z^2+4 z+5=0
चूँकि f(z) के सभी गुणांक वास्तविक और धनात्मक हैं, दिए गए समीकरण का कोई धनात्मक वास्तविक मूल नहीं है।इसके अलावा अगर हम z=-x रखते हैं,तो हमारे पास है:
f(-x) =x^4-2 x^3+3 x^2-4 x+5 \\ =x^2\left(x^2-2 x+1\right)+2\left(x^2-2 x+1\right)+3 \\ \Rightarrow f(-x)= x^2(x-1)^2+2(x-1)^2+3>0, \forall x
इससे पता चलता है कि दिए गए समीकरण का कोई ऋणात्मक वास्तविक मूल नहीं हो सकता है।फिर से z=iy रखने पर,हम प्राप्त करते हैं:
f(i y)=y^4-2 i y^3-3 y^2+4 i y+5 \\ \Rightarrow f(i y)=\left(y^4-3 y^2+5 \right)+2 i(2 y-y^3)
अब f(iy)=0 यदि और यदि केवल यदि समीकरण y^4-3 y^2+5=0 तथा 2 y-y^3=0 , y के समान मानों के लिए संतुष्ट हैं।लेकिन ये समीकरण असंगत हैं क्योंकि दूसरा समीकरण संतुष्ट है जब y=\sqrt{2} लेकिन पहला इस मान के लिए संतुष्ट नहीं है।इस प्रकार समीकरण का कोई विशुद्ध काल्पनिक मूल भी नहीं हो सकता है।
इस प्रकार हमने दिखाया है कि दिए गए समीकरण की वास्तविक या काल्पनिक अक्ष पर कोई मूल नहीं हैं।अब हम कोणांक सिद्धांत का उपयोग करके पहले चतुर्थांश में सम्मिश्र मूलों की खोज करते हैं।इस उद्देश्य के लिए हम \triangle \arg f(z)=0 अर्थात् arg f(z) में परिवर्तन पाते हैं क्योंकि z पहले चतुर्थांश के उस भाग के चारों ओर घूमता है जो |z|=R से घिरा होता है जहाँ R बड़ा होता है।हम लिखते हैं:
f(z)=w=u+iv
(a) x-अक्ष पर \triangle \arg f(z)=0 चूँकि जब z,0 से \infty तक x-अक्ष के अनुदिश गति करता है,तो वास्तविक u-अक्ष के अनुदिश 5 से \infty तक गति करता है अर्थात् w वास्तविक तथा धनात्मक रहता है जिससे धनात्मक x-अक्ष के प्रत्येक बिदु पर arg f(z)=0 चलता है।
(b)वृत्त |z|=R के चतुर्थांश पर,हम z=R e^{i \theta} लिखते हैं ताकि
f(z)=z^4\left(1+\frac{2}{z}+\frac{3}{z^2}+\frac{4}{z^3}+\frac{5}{z^4}\right) \\ \Rightarrow f(z)=R^4 e^{4 i \theta}[1+F(z)]
जहां F(z) \rightarrow 0 एकसमान रूप से z \rightarrow \infty के रूप में।इस प्रकार जब पहले चतुर्थांश का चक्कर लगाता है,तो arg f(z) में परिवर्तन होता है:
4 \cdot \frac{\pi}{2}=2 \pi
(c) y-अक्ष पर,z=iy लेने पर,हमें f(iy)=\left(y^4-3 y^2+5\right)+2 i\left(2 y-y^3\right) प्राप्त होता है ताकि \arg (i y)=\tan^{-1} \left(\frac{v}{u}\right) \\ \Rightarrow \arg (i y)=\tan ^{-1}\left(\frac{2 y(2-y^2)}{y^4-3y^2+5}\right) हो।
अब कोष्ठक में व्यंजक का अंश y=0 और y=\sqrt{2} के लिए गायब हो जाता है और इसका हर y के किसी भी मान के लिए गायब नहीं हो जाता है जबकि हमारे पास
y^4-3 y^2+5=\left(y^2-\frac{3}{2}\right)^2+\frac{11}{4} >0
सभी y के लिए।अब चर्चा करते हैं कि u-v समतल में (u,v) कैसे गमन करता है क्योंकि y, \infty से 0 तक मान ग्रहण करता है:
u=y^4-3 y^2+5, v=4 y-2 y^3
(i) जब \sqrt{2} < y< \infty ,u धनात्मक है और v ऋणात्मक है। y=\sqrt{2}, u=3,u=3 और v=0 पर भी जब y \rightarrow \infty, u \rightarrow \infty, v \rightarrow \infty
यह दिखाता है कि y, \infty से \sqrt{2} तक परिवर्तित होता है,बिंदु (u,v), \infty से शुरू होता है जहाँ वक्र u-अक्ष के समान्तर होता है:
( since \frac{v}{u} \rightarrow 0 जैसे y \rightarrow \infty )
और पहले चतुर्थांश में शेष u-अक्ष पर बिंदु (3,0) पर आता है।इससे पता चलता है कि arg f(z) में कोई परिवर्तन नहीं होता है क्योंकि y \infty से \sqrt{2} तक बदलता है।
(ii) जब 0< y< \sqrt{2} ,u और v दोनों धनात्मक हैं।y= 0,u=5,v=0 पर।
अतः जब y का मान \sqrt{2} से 0 तक बदलता है,तो बिंदु (u,v), (3,0) से शुरू होता है और पहले चतुर्थांश में शेष बिंदु u-अक्ष पर बिंदु (5,0) की ओर बढ़ता है ताकि फिर से कोणांक में कोई परिवर्तन न हो।
इस प्रकार f(z) के कोणांक में कुल परिवर्तन है:
0+2 \pi+0=2 \pi
अतः कोणांक सिद्धांत के अनुसार,पहले चतुर्थांश में f(z) के शून्यों की संख्या है:
\frac{1}{2 \pi} \times 2 \pi=1
इसी प्रकार,हम दूसरे चतुर्थांश में सम्मिश्र मूलों की संख्या ज्ञात कर सकते हैं,जिससे z को काल्पनिक अक्ष के 0 से R तक के खंड से युक्त बंद वक्र तक गमन करने दें,चतुर्थांश वृत्त
z=R e^{i \theta}, \frac{\pi}{2} \leq \theta \leq \pi
और वास्तविक अक्ष के -R से 0 तक का खंड और फिर R \rightarrow \infty दे रहा है।arg f(z) में कोई परिवर्तन नहीं होता है क्योंकि z अक्ष पर दो रेखाखंडों में से किसी एक के साथ चलता है और जब z वृत्त चतुर्थांश के साथ चलता है तो परिवर्तन 2 \pi होता है।इसलिए फिर से दूसरे चतुर्थांश में एक मूल है।
चूँकि दिए गए समीकरण के गुणांक सभी वास्तविक हैं,इसलिए मूल संयुग्मी युग्म में होनी चाहिए।इसलिए तीसरे और चौथे चतुर्थांशों में से प्रत्येक में एक मूल होना चाहिए।
Illustration:6.यदि f(z) , |z| < 1 के लिए विश्लेषिक है और यदि यह शर्त |f(z)|<1, f(0)=0 को संतुष्ट करता है; फिर दिखाएं कि |f(z)|<|z| और f'(0) <1।
(If f(z) is analytic for and if it satisfies the condition |f(z)|<1, f(0)=0 ;then show that |f(z)|<|z| and f'(0)<1 .)
Solution:मान लीजिए C वृत्त |z|=r(r<1) है।
अब,यह दिया गया है कि |z|=r(r<1) के लिए |f(z)|< 1 ,इसलिए f(z) वृत्त C के भीतर और उस पर विश्लेषिक है,इसलिए टेलर प्रमेय द्वारा
f(z)=\overset{\infty}{\underset{n=0}{\sum}} a_n z^n , C के अन्दर किसी z पर
=a_0+a_1 z+a_2 z^2+\cdots
दिया है;f(0)=0 इसलिए a_0=0 और इसलिए
f(z)=a_1 z+a_2 z^2+a_3 z^3+\cdots \\ \Rightarrow \frac{f(z)}{z}=a_1+a_2 z+a_3 z^2
लिखते हैं: F(z)=\frac{f(z)}{z}=a_1+a_2 z+a_3 z^z+\cdots
फ़ंक्शन F(z) में z=0 पर एक विचित्रता होती है जिसे हटा दिया जाता है यदि हम F(z)=a_{1} को परिभाषित करते हैं।
इसके अलावा F(0)=a_1=f^{\prime}(0) हमारे पास है [(1) से]
अब,चूँकि F(z),C के भीतर और उस पर विश्लेषिक है, अतः अधिकतम मापांक सिद्धांत द्वारा |F(z)|, C के ऊपर अधिकतम तक पहुंच जाता है परन्तु C के अन्दर नहीं।
यानी |F(z)|, C < max |F(z)| , z के अन्दर जो C पर पहुंचा जाता है।
=value of |F(z)| for |z|=r
=value of \frac{|f(z)|}{|z|} जबकि F(z)=\frac{f(z)}{z}
=value of \frac{|f(z)|}{|z|} (for |z|= r )
< \frac{1}{r} जबकि |f(z)|<1,|z|=r (r < 1) के लिए
\rightarrow 1 as r \rightarrow 1
i.e. |F(z)| <1 for |z| < 1
\Rightarrow \left|\frac{f(z)}{z}\right| < 1 since F(z)=\frac{f(z)}{z} \\ \Rightarrow |f(z)|< |z| for |z| < 1
विशेष रूप से |F(0)|< 1 [(2) में z=0 रखने पर ]
\Rightarrow \left|f^{\prime}(0)\right|< 1 since F_{0}=f^{\prime }(0)
इन परिणामों को श्वार्ज लेम्मा के रूप में जाना जाता है।
उपर्युक्त उदाहरणों के द्वारा सम्मिश्र विश्लेषण में समीकरण के मूल (Roots of Equation in Complex Analysis),सम्मिश्र विश्लेषण में समीकरण के मूल ज्ञात करना (To Find Roots of Equation in Complex Analysis) को समझ सकते हैं।
Also Read This Article:- Examples of Residue Theorem
3.सम्मिश्र विश्लेषण में समीकरण के मूल (Frequently Asked Questions Related to Roots of Equation in Complex Analysis),सम्मिश्र विश्लेषण में समीकरण के मूल ज्ञात करना (To Find Roots of Equation in Complex Analysis) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.अनन्तकी फलन के अनन्तक एवं शून्य का कथन लिखिए। (Write the Statement of a Memorphic Function):
उत्तर:मान लें f(z) संवृत्त परिरेखा पर तथा उसके अन्दर स्थित परिमित अनन्तकों के अतिरिक्त सभी बिन्दुओं पर विश्लेषिक है तथा मान लें कि C पर।यदि N तथा P क्रमशः C के अन्दर स्थित शून्यों एवं अनन्तकों की संख्या है (कोटि-m के प्रत्येक शून्य या अनन्तक की गणना m शून्य या m-अनन्तक की गयी है) तो
\frac{1}{2 \pi c} \int_c \frac{f^{\prime}(z)}{f(z)} d z=N-P
प्रश्न:2.कोणांक सिद्धान्त का कथन लिखिए। (Write the Statement of Argument Principle):
उत्तर:यदि परिरेखा C के अन्दर अवस्थित अनन्तकों के अतिरिक्त शेष क्षेत्र में तथा C पर यदि फलन f(z) विश्लेषिक है तथा C पर f(z) \neq 0 तो
N-P=\frac{1}{2 \pi} \Delta_C[\arg (f(z))]
यहाँ \Delta_C , \arg (f(z)) में विचरण को दर्शाता है जबकि z द्वारा संवृत्त परिरेखा C का एक बार परिभ्रमण किया जाता है (एक m-कोटि के अनन्तक या शून्य की गणना m बार की जाती है)।
प्रश्न:3.रुशे प्रमेय का कथन लिखिए। (Write the Statement of Rouche Theorem):
उत्तरःमान लें कि f(z) तथा g(z) संवृत्त परिरेखा C पर तथा उसके भीतर विश्लेषिक है तथा C पर प्रत्येक z के लिए |g(z)| < |f(z)| तो C के अन्दर f(z)+g(z) एवं f(z) के शून्यों की संख्या बराबर है।
उपर्युक्त प्रश्नों के उत्तर द्वारा सम्मिश्र विश्लेषण में समीकरण के मूल (Roots of Equation in Complex Analysis),सम्मिश्र विश्लेषण में समीकरण के मूल ज्ञात करना (To Find Roots of Equation in Complex Analysis) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Roots of Equation in Complex Analysis
सम्मिश्र विश्लेषण में समीकरण के मूल
(Roots of Equation in Complex Analysis)
Roots of Equation in Complex Analysis
सम्मिश्र विश्लेषण में समीकरण के मूल (Roots of Equation in Complex Analysis) के
इस आर्टिकल में समीकरण के मूल ज्ञात करने से सम्बन्धित सवालों को हल करके
समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.