Ellipse Class 11
1.दीर्घवृत्त कक्षा 11 (Ellipse Class 11),कक्षा 11 में दीर्घवृत्त (Ellipse in Class 11):
दीर्घवृत्त कक्षा 11 (Ellipse Class 11) के इस आर्टिकल में दीर्घवृत्त की नाभियों,शीर्षों के निर्देशांक,दीर्घ और लघु अक्ष की लम्बाइयाँ,उत्केन्द्रता तथा नाभिलम्ब जीवा की लम्बाई और दीर्घवृत्त का समीकरण ज्ञात करना सीखेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Circle Class 11
2.दीर्घवृत्त कक्षा 11 के साधित उदाहरण (Illustration Based on Ellipse Class 11):
निम्नलिखित प्रश्नों 1 से 9 तक प्रत्येक दीर्घवृत्त में नाभियों और शीर्षों के निर्देशांक,दीर्घ और लघु अक्ष की लम्बाइयाँ,उत्केन्द्रता तथा नाभिलम्ब जीवा की लम्बाई ज्ञात कीजिए:
Illustration:1. \frac{x^2}{36}+\frac{y^2}{16}=1
Solution: \frac{x^2}{36}+\frac{y^2}{16}=1 \\ \frac{x^2}{36} का हर \frac{y^2}{16} के हर से बड़ा है,इसलिए दीर्घ-अक्ष x-अक्ष के अनुदिश है।अतः दिए गए समीकरण की \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 से तुलना करने पर:
a^2=36 \Rightarrow a=6, b^2=16 \Rightarrow b=4
साथ ही C=\sqrt{a^2-b^2}=\sqrt{36-16} \\ \Rightarrow C=\sqrt{20}=2 \sqrt{5}
अतः नाभियों के निर्देशांक ( \pm C, 0)=( \pm 2 \sqrt{5}, 0)
शीर्षों के निर्देशांक ( \pm a, 0)=( \pm 6,0)
दीर्घ अक्ष की लम्बाई 2a=2×6=12
लघु अक्ष की लम्बाई 2b=2×4=8
उत्केन्द्रता e=\frac{c}{a}=\frac{2 \sqrt{5}}{6}=\frac{\sqrt{5}}{3}
और नाभिलम्ब जीवा की लम्बाई =\frac{2 b^2}{a} \\ =\frac{2 \times 16}{6}=\frac{16}{3}
Illustration:2. \frac{x^2}{4}+\frac{y^2}{25}=1
Solution: \frac{x^2}{4}+\frac{y^2}{25}=1 \\ \frac{y^2}{25} का हर \frac{x^2}{4} के हर से बड़ा है,इसलिए दीर्घ-अक्ष y-अक्ष के अनुदिश है।अतः दिए गए समीकरण की \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 से तुलना करने पर:
b^2=4 \Rightarrow b=2, a^2=25 \Rightarrow a=5
साथ ही C=\sqrt{a^2-b^2}=\sqrt{25-4}=\sqrt{21}
अतः नाभियों के निर्देशांक F(0, \pm C)=(0, \pm \sqrt{21})
शीर्षों के निर्देशांक V(0, \pm a)=(0, \pm 5)
दीर्घ अक्ष की लम्बाई=2a=2×5=10
लघु अक्ष की लम्बाई=2b=2×4=8
उत्केन्द्रता (e)=\frac{c}{a}=\frac{\sqrt{2}}{5}
और नाभिलम्ब जीवा की लम्बाई=\frac{2 b^2}{a} \\ =\frac{2 \times 4}{5}=\frac{8}{5}
Illustration:3. \frac{x^2}{16}+\frac{y^2}{9}=1
Solution: \frac{x^2}{16}+\frac{y^2}{9}=1 \\ \frac{x^2}{16} का हर \frac{y^2}{9} के हर से बड़ा है,इसलिए दीर्घ-अक्ष x-अक्ष के अनुदिश है।अतः दिए गए समीकरण की \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 से तुलना करने पर:
a^2=16 \Rightarrow a=4, b^2=9 \Rightarrow b=3
साथ ही C=\sqrt{a^2-b^2}=\sqrt{16-9}=\sqrt{7}
अतः नाभियों के निर्देशांक F(\pm C, 0)=F( \pm \sqrt{7}, 0)
शीर्षों के निर्देशांक V( \pm a, 0)=V( \pm 4,0)
दीर्घ अक्ष की लम्बाई 2a=2×4=8
लघु अक्ष की लम्बाई 2b=2×3=6
उत्केन्द्रता (e)=\frac{c}{a}=\frac{\sqrt{7}}{4}
और नाभिलम्ब जीवा की लम्बाई=\frac{2 b^2}{a} \\ =\frac{2 \times 9}{4}=\frac{9}{2}
Illustration:4. \frac{x^2}{25}+\frac{y^2}{100}=1
Solution: \frac{x^2}{25}+\frac{y^2}{100}=1 \\ \frac{y^2}{100} का हर \frac{x^2}{25} के हर से बड़ा है,इसलिए दीर्घ-अक्ष y-अक्ष के अनुदिश है।अतः दिए गए समीकरण की \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 से तुलना करने पर:
b^2=25 \Rightarrow b=5, \quad a^2=100 \Rightarrow a=10
साथ ही C=\sqrt{a^2-b^2}=\sqrt{100-25}=\sqrt{75}
अतः नाभियों के निर्देशांक F(0, \pm C)=F(0, \pm \sqrt{75})
शीर्षों के निर्देशांक V(0, \pm a)=V(0, \pm 10)
दीर्घ अक्ष की लम्बाई=2a=2×10=20
लघु अक्ष की लम्बाई=2b=2×5=10
उत्केन्द्रता (e)=\frac{c}{a}=\frac{\sqrt{75}}{10}=\frac{\sqrt{3}}{2}
और नाभिलम्ब जीवा की लम्बाई =\frac{2 b^2}{a } \\ =\frac{2 \times 25}{10}=5
Illustration:5. \frac{x^2}{49}+\frac{y^2}{36}=1
Solution: \frac{x^2}{49}+\frac{y^2}{36}=1 \\ \frac{x^2}{49} का हर \frac{y^2}{36} के हर से बड़ा है,इसलिए दीर्घ-अक्ष x-अक्ष के अनुदिश है।अतः दिए गए समीकरण की \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 से तुलना करने पर:
a^2=49 \Rightarrow a=7, b^2=36 \Rightarrow b=6
साथ ही C=\sqrt{a^2-b^2}=\sqrt{49-36}=\sqrt{13}
अतः नाभियों के निर्देशांक F( \pm C, 0)=F( \pm \sqrt{13}, 0)
शीर्षों के निर्देशांक V( \pm a, 0)=V( \pm 7,0)
दीर्घ अक्ष की लम्बाई=2a=2×7=14
लघु अक्ष की लम्बाई=2b=2×6=12
उत्केन्द्रता (e)=\frac{c}{a}=\frac{\sqrt{13}}{7}
और नाभिलम्ब जीवा की लम्बाई =\frac{2 b^2}{a} \\ =\frac{2 \times 36}{7}=\frac{72}{7}
Illustration:6. \frac{x^2}{100}+\frac{y^2}{400}=1
Solution: \frac{x^2}{100}+\frac{y^2}{400}=1 \\ \frac{y^2}{400} का हर \frac{x^2}{100} के हर से बड़ा है,इसलिए दीर्घ-अक्ष y-अक्ष के अनुदिश है।अतः दिए गए समीकरण की \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 से तुलना करने पर:
b^2=10 \Rightarrow b=10, a^2=400 \Rightarrow a=20
साथ ही C=\sqrt{a^2-b^2}=\sqrt{400-100}=\sqrt{300} \\ \Rightarrow C=10 \sqrt{3}
अतः नाभियों के निर्देशांक F(0, \pm C)=F(0, \pm 10 \sqrt{3})
शीर्षों के निर्देशांक V(0, \pm a)=V(0, \pm 20)
दीर्घ अक्ष की लम्बाई=2a=2×20=40
लघु अक्ष की लम्बाई=2b=2×10=20
उत्केन्द्रता (e)=\frac{C}{a}=\frac{10 \sqrt{3}}{20}=\frac{\sqrt{3}}{2}
और नाभिलम्ब जीवा की लम्बाई =\frac{2 b^2}{a} \\ =\frac{2 \times 100}{20}=10
Illustration:7. 36 x^2+4 y^2=144
Solution: 36 x^2+4 y^2=144 \\ \Rightarrow \frac{36 x^2}{144}+\frac{4 y^2}{144}=1 \\ \Rightarrow \frac{x^2}{4}+\frac{y^2}{36}=1 \\ \frac{y^2}{36} का हर \frac{x^2}{4} के हर से बड़ा है,इसलिए दीर्घ-अक्ष y-अक्ष के अनुदिश है।अतः दिए गए समीकरण की \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 से तुलना करने पर:
b^2=4 \Rightarrow b=2, a^2=36 \Rightarrow a=6
साथ ही C=\sqrt{a^2-b^2}=\sqrt{36-4}=\sqrt{32} \\ \Rightarrow C=4 \sqrt{2}
अतः नाभियों के निर्देशांक F(0, \pm C)=F(0, \pm 40)
शीर्षों के निर्देशांक V(0, \pm a)=V(0, \pm 6)
दीर्घ अक्ष की लम्बाई=2a=2×6=12
लघु अक्ष की लम्बाई=2b=2×2=4
उत्केन्द्रता (e)=\frac{C}{a}=\frac{4 \sqrt{2}}{6}=\frac{2 \sqrt{2}}{3}
और नाभिलम्ब जीवा की लम्बाई =\frac{2 b^2}{a} \\ =\frac{2 \times 4}{6}=\frac{4}{3}
Illustration:8. 16 x^2+y^2=16
Solution: 16 x^2+y^2=16 \\ \Rightarrow \frac{16 x^2}{16}+\frac{y^2}{16}=1 \\ \Rightarrow \frac{x^2}{1}+\frac{y^2}{16}=1
\frac{y^2}{16} का हर \frac{x^2}{1} के हर से बड़ा है,इसलिए दीर्घ-अक्ष y-अक्ष के अनुदिश है।अतः दिए गए समीकरण की \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 से तुलना करने पर:
b^2=1 \Rightarrow b=1, a^2=16 \Rightarrow a=4
साथ ही C=\sqrt{a^2-b^2}=\sqrt{16-1}=\sqrt{15}
अतः नाभियों के निर्देशांक F(0, \pm C)=F(0, \pm \sqrt{15})
शीर्षों के निर्देशांक V(0, \pm a)=V(0, \pm 4)
दीर्घ अक्ष की लम्बाई=2a=2×4=8
लघु अक्ष की लम्बाई=2b=2×1=2
उत्केन्द्रता (e)=\frac{C}{a}=\frac{\sqrt{15}}{4}
और नाभिलम्ब जीवा की लम्बाई =\frac{2 b^2}{a} \\ =\frac{2 \times 1}{4}=\frac{1}{2}
Illustration:9. 4 x^2+9 y^2=36
Solution: 4 x^2+9 y^2=36 \\ \Rightarrow \frac{4 x^2}{36}+\frac{9 y^2}{36}=1 \\ \Rightarrow \frac{x^2}{9}+\frac{y^2}{4}=1
\frac{x^2}{9} का हर \frac{y^2}{4} के हर से बड़ा है,इसलिए दीर्घ-अक्ष x-अक्ष के अनुदिश है।अतः दिए गए समीकरण की \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 से तुलना करने पर:
a^2=9 \Rightarrow a=3, b^2=4 \Rightarrow b=2
साथ ही C=\sqrt{a^2-b^2}=\sqrt{9-4}=\sqrt{5}
अतः नाभियों के निर्देशांक F( \pm C, 0)=F( \pm \sqrt{5}, 0)
शीर्षों के निर्देशांक V( \pm a, 0)=v( \pm 3,0)
दीर्घ अक्ष की लम्बाई=2a=2×3=6
लघु अक्ष की लम्बाई=2b=2×2=4
उत्केन्द्रता (e)=\frac{c}{a}=\frac{\sqrt{5}}{3}
और नाभिलम्ब जीवा की लम्बाई =\frac{2 b^2}{a} \\ =\frac{2 \times 4}{3}=\frac{8}{3}
निम्नलिखित प्रश्नों 10 से 20 तक प्रत्येक में दिए प्रतिबन्धों को सन्तुष्ट करते हुए दीर्घवृत्त का समीकरण ज्ञात कीजिए:
Illustration:10.शीर्षों ( \pm 5,0),नाभियाँ ( \pm 4,0)
Solution:शीर्षों ( \pm 5,0),नाभियाँ ( \pm 4,0)
क्योंकि दीर्घवृत्त का शीर्ष x-अक्ष पर स्थित है अतः इसका समीकरण \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 के अनुरूप होगा,जहाँ अर्ध-दीर्घ अक्ष की लम्बाई a है।हमें ज्ञात है,कि a=5 , c= \pm 4
अतः C^2=a^2-b^2 से
4^2=5^2-b^2 \\ b^2=25-16 \\ \Rightarrow b^2=9
अतः \frac{x^2}{25}+\frac{y^2}{9}=1
Illustration:11.शीर्षों (0, \pm 13),नाभियाँ (0, \pm 5)
Solution:शीर्षों (0, \pm 13),नाभियाँ (0, \pm 5)
क्योंकि दीर्घवृत्त का शीर्ष y-अक्ष पर स्थित है अतः इसका समीकरण \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 के अनुरूप होगा,जहाँ अर्ध-दीर्घ अक्ष की लम्बाई a है।हमें ज्ञात है कि a=13,C=\pm 5
अतः C^2=a^2-b^2 सूत्र से
( \pm 5)^2=(13)^2-b^2 \Rightarrow b^2=169-25 \\ \Rightarrow b^2=144
अतः \frac{x^2}{144}+\frac{y^2}{169}=1
Illustration:12.शीर्षों ( \pm 6,0) ,नाभियाँ ( \pm 4,0)
Solution:शीर्षों ( \pm 6,0) ,नाभियाँ ( \pm 4,0)
क्योंकि दीर्घवृत्त का शीर्ष x-अक्ष पर स्थित है अतः इसका समीकरण \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 के अनुरूप होगा,जहाँ अर्ध-दीर्घ अक्ष की लम्बाई a है।हमें ज्ञात है,कि a=6, C=\pm 4
अतः C^2=a^2-b^2 सूत्र से
(\pm 4)^2=6^2-b^2 \\ \Rightarrow b^2=36-16 \\ \Rightarrow b^2=20
अतः \frac{x^2}{36}+\frac{y^2}{20}=1
Illustration:13.दीर्घ अक्ष के अंत्य बिन्दु ( \pm 3,0) ,लघु अक्ष के अंत्य बिन्दु (0, \pm 2)
Solution:दीर्घ अक्ष के अंत्य बिन्दु ( \pm 3,0) ,लघु अक्ष के अंत्य बिन्दु (0, \pm 2)
क्योंकि दीर्घ अक्ष के अंत्य बिन्दु x-अक्ष पर स्थित हैं अतः इसका समीकरण \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 के अनुरूप होगा,जहाँ अर्ध-दीर्घ अक्ष की लम्बाई a है।हमें ज्ञात है,कि a=3,b=2
अतः \frac{x^2}{9}+\frac{y^2}{4}=1
Illustration:14.दीर्घ अक्ष के अंत्य बिन्दु (0, \pm \sqrt{5}) ,लघु अक्ष के अंत्य बिन्दु ( \pm 1,0)
Solution:दीर्घ अक्ष के अंत्य बिन्दु (0, \pm \sqrt{5}) ,लघु अक्ष के अंत्य बिन्दु ( \pm 1,0)
क्योंकि दीर्घ अक्ष के अंत्य बिन्दु y-अक्ष पर स्थित हैं अतः इसका समीकरण \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 के अनुरूप होगा,जहाँ अर्ध-दीर्घ अक्ष की लम्बाई a है।हमें ज्ञात है,कि a=\sqrt{5}, b=1
अतः \frac{x^2}{1}+\frac{y^2}{5}=1
Illustration:15.दीर्घ अक्ष की लम्बाई 26,नाभियाँ ( \pm 5,0)
Solution:दीर्घ अक्ष की लम्बाई 26,नाभियाँ ( \pm 5,0)
क्योंकि नाभियाँ x-अक्ष पर स्थित हैं,इसलिए दीर्घवृत्त का समीकरण \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 के अनुरूप है।
दिया है a=अर्ध-दीर्घ अक्ष=\frac{26}{2}=13
और सूत्र C^2=a^2-b^2 से
\Rightarrow( \pm 5)^2=13^2-b^2 \\ \Rightarrow b^2=169-25 \\ \Rightarrow b^2=144
अतः \frac{x^2}{169}+\frac{y^2}{144}=1
Illustration:16.लघु अक्ष की लम्बाई 26,नाभियाँ (0, \pm 6)
Solution:लघु अक्ष की लम्बाई 26,नाभियाँ (0, \pm 6)
क्योंकि नाभियाँ y-अक्ष पर स्थित हैं,इसलिए दीर्घवृत्त का समीकरण \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 के अनुरूप है।
दिया है b=अर्ध-लघु अक्ष=\frac{16}{2}=8
तथा C=\pm 6
और सूत्र C^2=a^2-b^2 से
( \pm 6)^2=a^2-(8)^2 \\ \Rightarrow a^2=36+64=100
अतः \frac{x^2}{64}+\frac{y^2}{100}=1
Illustration:17.नाभियाँ ( \pm 3,0), a=4
Solution:नाभियाँ ( \pm 3,0), a=4
क्योंकि नाभियाँ x-अक्ष पर स्थित हैं,इसलिए दीर्घवृत्त का समीकरण \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 के अनुरूप है।
दिया है a=4 (अर्ध-दीर्घ अक्ष)
तथा C=\pm 3
और सूत्र c^2=a^2-b^2 से
( \pm 3)^2=(4)^2-b^2 \\ \Rightarrow b^2=16-9=7
अतः \frac{x^2}{16}+\frac{y^2}{7}=1
Illustration:18.b=3,c=4,केन्द्र मूलबिन्दु पर,नाभियाँ x-अक्ष पर
Solution:b=3,c=4,केन्द्र मूलबिन्दु पर,नाभियाँ x-अक्ष पर
नाभियाँ x-अक्ष पर स्थित हैं,इसलिए दीर्घवृत्त का समीकरण \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 के अनुरूप है।
दिया है b=3,c=4
और सूत्र C^2=a^2-b^2 से
(4)^2=a^2-(3)^2 \\ \Rightarrow 16=a^2-9 \\ \Rightarrow a^2=16+9=25
अतः \frac{x^2}{25}+\frac{y^2}{9}=1
Illustration:19.केन्द्र (0,0) पर दीर्घ-अक्ष,y-अक्ष पर और बिन्दुओं (3,2) और (1,6) से जाता है।
Solution:केन्द्र (0,0) पर दीर्घ-अक्ष,y-अक्ष पर और बिन्दुओं (3,2) और (1,6) से जाता है।
क्योंकि दीर्घ-अक्ष y-अक्ष पर स्थित है तथा केन्द्र (0,0) है अतः दीर्घवृत्त का समीकरण \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 के अनुरूप है।
यह (3,2) और (1,6) से गुजरता है अतः
\frac{9}{b^2}+\frac{4}{a^2}=1 \cdots(1) \\ \frac{1}{b^2}+\frac{36}{a^2}=1 \cdots(2)
समीकरण (1) को 9 से गुणा करने पर:
\frac{81}{b^2}+\frac{36}{a^2}=9 \cdots(3)
समीकरण (3) में से समीकरण (2) घटाने पर:
\frac{80}{b^2}=8 \Rightarrow b^2=\frac{80}{8}=10 \\ b^2 का मान समीकरण (1) में रखने पर:
\frac{9}{10}+\frac{4}{a^2}=1 \\ \Rightarrow \frac{4}{a^2}=1-\frac{9}{10} \\ \Rightarrow \frac{4}{a^2}=\frac{1}{10} \Rightarrow a^2=40
अतः दीर्घवृत्त का समीकरण:
\frac{x^2}{10}+\frac{y^2}{40}=1
Illustration:20.दीर्घ अक्ष,x-अक्ष पर और बिन्दुओं (4,3) और (6,2) से जाता है।
Solution:दीर्घ अक्ष,x-अक्ष पर और बिन्दुओं (4,3) और (6,2) से जाता है।
दीर्घ अक्ष x-अक्ष पर स्थित है अतः दीर्घवृत्त का समीकरण \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 के अनुरूप है।
यह (4,3) और (6,2) से गुजरता है अतः
\frac{16}{a^2}+\frac{9}{b^2}=1 \cdots(1)\\ \frac{36}{a^2}+\frac{4}{b^2}=1 \cdots(2)
समीकरण (1) को 4 से तथा (2) को 9 से गुणा करने पर:
\frac{64}{a^2}+\frac{36}{b^2}=4 \cdots(3) \\ \frac{324}{a^2}+\frac{36}{b^2}=9 \cdots(4)
समीकरण (4) में से (3) को घटाने पर:
\frac{260}{a^2}=5 \Rightarrow a^2=\frac{260}{5}=52 \\ a^2 का मान समीकरण (1) में रखने पर:
\frac{16}{52}+\frac{9}{b^2}=1 \Rightarrow \frac{9}{b^2}=1-\frac{16}{52} \\ \Rightarrow \frac{9}{b^2}=\frac{36}{52} \Rightarrow b^2=\frac{9 \times 52}{36}=13
अतः दीर्घवृत्त का समीकरण:
\frac{x^2}{52}+\frac{y^2}{13}=1
उपर्युक्त उदाहरणों के द्वारा दीर्घवृत्त कक्षा 11 (Ellipse Class 11),कक्षा 11 में दीर्घवृत्त (Ellipse in Class 11) को समझ सकते हैं।
3.दीर्घवृत्त कक्षा 11 पर आधारित समस्याएं (Problems Based on Ellipse Class 11):
निम्नलिखित दीर्घवृत्तों की उत्केन्द्रता,नाभिलम्ब और नाभियों के निर्देशांक ज्ञात कीजिए:
(1.) 3 x^2+4 y^2=12
(2.) 9 x^2+5 y^2-30 y=0
उत्तर (Answers):(1.) उत्केन्द्रता (e)=\frac{1}{2} ,नाभिलम्ब =\frac{2 b^2}{a}=\frac{10}{3} ,नाभि के निर्देशांक ( \pm C, 0)=( \pm 1,0)
(2.)उत्केन्द्रता (e)=\frac{2}{3}, नाभिलम्ब \frac{2 b^2}{a}=3,नाभि के निर्देशांक (0,1) तथा (0,5)
उपर्युक्त सवालों को हल करने पर दीर्घवृत्त कक्षा 11 (Ellipse Class 11),कक्षा 11 में दीर्घवृत्त (Ellipse in Class 11) को ठीक से समझ सकते हैं।
Also Read This Article:- Parabola Class 11
4.दीर्घवृत्त कक्षा 11 (Frequently Asked Questions Related to Ellipse Class 11),कक्षा 11 में दीर्घवृत्त (Ellipse in Class 11) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.दीर्घवृत्त की परिभाषा दीजिए। (Define Ellipse):
उत्तर:एक दीर्घवृत्त तल के उन बिन्दुओं का समुच्चय है जिनका तल में दो स्थिर बिन्दुओं से दूरी का योग अचर होता है।
प्रश्न:2.दीर्घवृत्त की नाभियाँ किसे कहते हैं? (What are the Foci of Ellipse?):
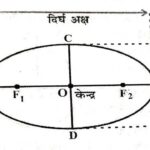
उत्तर:दो स्थिर बिन्दुओं को नाभियाँ कहते हैं।चित्र में F_{1},F_{2} नाभियाँ हैं।
प्रश्न:3.दीर्घवृत्त के दीर्घ अक्ष और लघु अक्ष को परिभाषित करो। (Define the Major Axis and Minor Axis of Ellipse):
उत्तर:नाभियों को मिलाने वाले रेखाखण्ड के मध्य बिन्दु को दीर्घवृत्त का केन्द्र कहते हैं।दीर्घवृत्त की नाभियों से जाने वाला रेखाखण्ड,दीर्घवृत्त का दीर्घ अक्ष (Major Axis) कहलाता है और केन्द्र से जाने वाला और दीर्घ अक्ष पर लम्बवत रेखाखण्ड,दीर्घवृत्त का लघु अक्ष (Minor axis) कहलाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा दीर्घवृत्त कक्षा 11 (Ellipse Class 11),कक्षा 11 में दीर्घवृत्त (Ellipse in Class 11) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Ellipse Class 11
दीर्घवृत्त कक्षा 11 (Ellipse Class 11)
Ellipse Class 11
दीर्घवृत्त कक्षा 11 (Ellipse Class 11) के इस आर्टिकल में दीर्घवृत्त की नाभियों,शीर्षों के निर्देशांक
,दीर्घ और लघु अक्ष की लम्बाइयाँ,उत्केन्द्रता तथा नाभिलम्ब जीवा की लम्बाई और दीर्घवृत्त
का समीकरण ज्ञात करना सीखेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.








