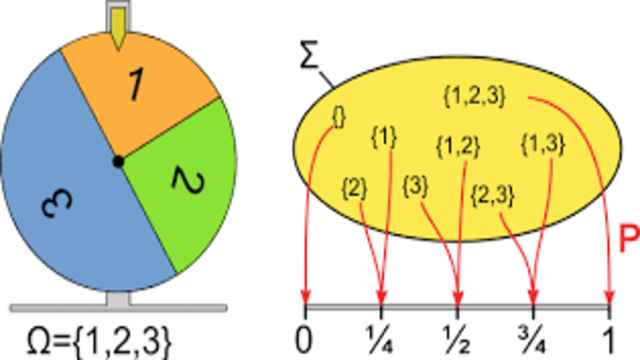
Three approaches to probability
1.प्रायिकता के लिए तीन दृष्टिकोण: शास्त्रीय, आवृत्ति-आधारित और व्यक्तिपरक दृष्टिकोण (Three approaches to probability: Classical, frequency-based and subjective approaches):
- प्रायिकता के लिए तीन दृष्टिकोण: शास्त्रीय, आवृत्ति-आधारित और व्यक्तिपरक दृष्टिकोण (Three approaches to probability: Classical, frequency-based and subjective approaches)है । अनिश्चितता को प्रबंधित करने के लिए प्रायिकता को एक उपकरण के रूप में परिभाषित किया जा सकता है। जब भी कोई घटना न तो निश्चित होती है (प्रायिकता = 1 के साथ) और न ही असंभव एक (संभावना = 0), तो हम अनिश्चित स्थिति का सामना कर रहे हैं, इसलिए हमें अपने ईवेंट को घटित होने की संभावना का पता लगाने की आवश्यकता है, जो कि वास्तव में, संभावना है।
इस लेख में, मैं प्रायिकता के लिए तीन दृष्टिकोण प्रस्तुत करने जा रहा हूं, जो उस अवधारणा की अलग व्याख्या और आरंभ करने के लिए अलग-अलग धारणा प्रदान करते हैं।
(1.)प्रायिकता के लिए तीन दृष्टिकोण का प्रथम दृष्टिकोण -शास्त्रीय दृष्टिकोण (The first approach to the three approaches to probability – the classical approach):
- यह दृष्टिकोण उस क्षेत्र में वापस आ जाता है जहाँ प्रायिकता को पहले सिस्टेमेटिक रूप से नियोजित किया गया था, जो कि जुआ है (सिक्कों को उछालना, पासा और आगे की तरफ उछालना)। जुआ समस्याओं की विशेषता यादृच्छिक प्रयोगों से होती है, जिनके संभावित परिणाम समान रूप से होते हैं। इसका मतलब यह है कि उनमें से कोई भी अन्य लोगों की तुलना में अधिक या कम होने की संभावना नहीं है, इसलिए उन्हें सममित स्थिति में कहा जाता है।
Also Read This Article-Simplification of question with solution
- शास्त्रीय दृष्टिकोण का विचार यह है कि, n से बाहर k तत्वों का एक संग्रह दिया गया है (जहाँ 0≤k approachn), उस संग्रह के द्वारा ई को दर्शाने वाली घटना E के घटित होने की संभावना बराबर है:
K/n
- आपको अंतर्ज्ञान देने के लिए, कल्पना करें कि आप एक पासा निकाल रहे हैं और आप परिणामों के निम्नलिखित संग्रह की संभावना का अनुमान लगाना चाहते हैं:
1/6, 2/6, 2/6, 6/6, 3/6
- हम जानते हैं कि संभव परिणाम 6 हैं। घटना “एक” 6 परिणामों में से 1 है, इसलिए इसकी संभावना 1/6 है। इसी तरह, घटना “पांच या छह या एक” (वह घटना, जिसमें उन संख्याओं में से एक निकलता है) 6 में से 3 परिणामों का प्रतिनिधित्व करती है, इसलिए प्रायिकता 3/6 = 0.5 होगी।
- शास्त्रीय दृष्टिकोण बहुत सहज है, फिर भी यह कुछ नुकसान से ग्रस्त है:
समरूपता की धारणा बहुत मजबूत और अतार्किक है। अर्थात्, कल्पना कीजिए कि आप घटना की प्रायिकता जानना चाहते हैं “कल मैं एक कार दुर्घटना होगी”। इस परिदृश्य के संभावित परिणाम दो हैं: कार दुर्घटना होना या कार दुर्घटना नहीं होना। यह देखते हुए कि k = एक कार दुर्घटना होने पर, उस घटना की प्रायिकता 1/2 है, जो थोड़ा चिंताजनक होने के अलावा, घटना की वास्तविक संभावना का प्रतिनिधि नहीं है। - इस दृष्टिकोण में, सूचना की अवधारणा के लिए कोई जगह नहीं है, जो सख्ती से प्रायिकता से संबंधित है। चलो पासा के पिछले उदाहरण के बारे में सोचते हैं। आपको बता दें कि यह पासा भरा हुआ है और संख्या “एक” होने के बजाय, इसमें दो “छह” हैं (इसलिए चेहरे 2,3,4,5,6,6 होंगे)। इस जानकारी के साथ, आप किस प्रायिकता के साथ इस घटना को “एक” बताएंगे? चूंकि यह असंभव है, प्रायिकता शून्य के बराबर है और 1/6 नहीं है। इसलिए, प्रायिकता उपलब्ध सूचना पर निर्भर करती है (व्यक्तिपरक दृष्टिकोण में अंतर्ज्ञान स्पष्ट होगा)
(2.)प्रायिकता के लिए आवृत्ति-आधारित (या अनुभवजन्य) दृष्टिकोण (Frequency-based (or empirical) approach to probability):
- इस दृष्टिकोण को औपचारिक रूप से प्राकृतिक विज्ञान के क्षेत्र में पेश किया गया था, जहां सममित स्थिति की धारणा खराब रूप से विफल हो जाती है। इसके बजाय, जिस विचार पर यह दृष्टिकोण आधारित है, वह यह है कि कई प्रयोगों को कुछ शर्तों के बराबर चलाया जा सकता है। प्रत्येक प्रयोग सफलता के लिए या असफल हो सकता है। इसलिए, सम-विषम परिस्थितियों में चलाए जा रहे n यादृच्छिक प्रयोग, हम “सफलता” की आवृत्ति को परिभाषित करते हैं (जो कि E घटना है):
fn(E)=number of success in a experiments/n
- यदि हम “परिवर्तन के अनुभवजन्य नियम” पर विचार करते हैं, जो बताता है कि अधिक n बढ़ता है, तो अधिक स्थिर आवृत्ति बन जाती है, हम निष्कर्ष निकाल सकते हैं कि n-> अनंत के लिए, उस आवृत्ति की सीमा मौजूद है, और यह बराबर है घटना की प्रायिकता “सफलता”:
- निम्न उदाहरण के साथ आवृत्ति-आधारित और शास्त्रीय दृष्टिकोण के बीच अंतर को आकार दें। कल्पना कीजिए कि आप अपने उछाले सिक्के के परिणाम की संभावना जानना चाहते हैं “सिर”। आप अपने शास्त्रीय दृष्टिकोण के साथ शुरू करते हैं: चूंकि संभव n परिणाम दो (सिर या पूंछ) हैं, “सिर” की प्रायिकता 1/2 = 0.5 है।
- अब आप अनुभवजन्य दृष्टिकोण का पालन करने का निर्णय लेते हैं, और आप अपने सिक्के को कई बार उछालना शुरू करते हैं, मान लीजिए कि 100 हैं। आपके प्रयासों में से, आपने 55 “हेड” और 45 “टेल” प्राप्त किए हैं। इसलिए, घटना “हेड” की आवृत्ति 55/100 = 0.55 है, और यह घटना “हेड” की प्रायिकता का अनुमान लगा सकती है।
- जैसा कि आप देख सकते हैं, हमने एक ही घटना के लिए दो अलग-अलग संभावनाएं (0.5 बनाम o.55) प्राप्त कीं। मुख्य अंतर सूचना की भूमिका है: 100 प्रयोगों के बाद, आपने अनुभवजन्य साक्ष्य एकत्र किए कि “सिर” “पूंछ” की तुलना में अधिक बार हुआ: यह हो सकता है कि आपका सिक्का सही नहीं है, और आप अपने निष्कर्षों को तैयार करते समय इस जानकारी को शामिल कर सकते हैं।
- इस दृष्टिकोण में आलोचनाओं की कमी नहीं है:
- फिर, एक बड़ी धारणा है जो आवृत्ति की अभिसरण गुणधर्म है, जिसकी सीमा मौजूद नहीं हो सकती है
समतुल्य परिस्थितियों में प्रयोगों को दोहराना संभव नहीं हो सकता है
ऐसी घटनाएं बहुत दुर्लभ हैं, जिनके लिए कई सिमुलेशन चलाना असंभव है (सुनामी जैसी चरम प्राकृतिक घटनाओं के बारे में सोचें)।
(3.)प्रायिकता के लिए आत्मनिष्ठ दृष्टिकोण (Subjective approach to probability):
- प्रोबेबिलिस्ट बी डी फिनेटी द्वारा विकसित, यह प्रायिकता की सबसे सहज परिभाषा है। वास्तव में, उस दृष्टिकोण के अनुसार, किसी घटना की प्रायिकता विश्वास की डिग्री है जो एक व्यक्ति उस घटना के साथ संलग्न होता है, जो उसकी उपलब्ध जानकारी के आधार पर होती है। यह तर्क तर्कसंगतता की धारणा के तहत है, जो मानता है कि लोग सुसंगत रूप से कार्य करते हैं।
- आइए एक अधिक विशिष्ट परिभाषा प्रदान करें। एक लॉटरी की कल्पना करें जहां आप घटना ई होने पर एस के बराबर धनराशि जीत सकते हैं। भाग लेने के लिए, आपको एक टिकट खरीदना होगा। अब, वह कौन सी कीमत है जिसे आप लॉटरी में भाग लेने के लिए भुगतान करने के लिए तैयार होंगे? यदि आप उस मूल्य को π (ई, एस) के रूप में इंगित करते हैं, तो ई की प्रायिकता E द्वारा दी गई है:
P(E)=π(E,S)/S
- कल्पना कीजिए कि आप इस संभावना की भविष्यवाणी करना चाहते हैं कि आपकी पसंदीदा फुटबॉल टीम कल मैच जीतेगी। आपके पास लॉटरी में भाग लेने की संभावना है, जहां अगर टीम जीतती है, तो आप 1000 € का पुरस्कार प्राप्त करते हैं, अन्यथा आप कुछ भी हासिल नहीं करते हैं। वह कौन सी कीमत है जिसे आप भाग लेने के लिए देने को तैयार हैं? मान लें कि आप अपनी टीम की क्षमताओं के बारे में बहुत आश्वस्त हैं और आप 700 € का भुगतान करने को तैयार हैं। इसलिए, आपकी टीम मैच जीतने की संभावना कल है:
P(“Win”)=π(“win”,1000)/1000
=700/1000=0.7
- यह अंतिम दृष्टिकोण गंभीर आलोचनाओं की गणना नहीं करता है, क्योंकि यह पिछले दृष्टिकोणों के कुछ नुकसानों को हल करता है (जैसे कि कई परिस्थितियों की विशिष्टता के कारण, समान परिस्थितियों में दोहराए जाने वाले प्रयोगों की असंभवता) और, एक ही समय में, अन्य सिद्धांतों के विपरीत नहीं है। । दरअसल, मूल्यांकनकर्ता को लॉटरी की कीमत तय करनी होती है, उसे प्रयोग करने से रोका नहीं जाता, सफलताओं की आवृत्ति की गणना की जाती है और मूल्य का प्रस्ताव करने के लिए इस जानकारी का उपयोग किया जाता है।
मूल रूप से, अन्य दृष्टिकोणों में क्या नियम था, व्यक्तिपरक दृष्टिकोण में एक विकल्प है। - उपर्युक्त विवरण में प्रायिकता के लिए तीन दृष्टिकोण (Three approaches to probability) के बारे में बताया गया है।
2.प्रायिकता के लिए तीन दृष्टिकोण (Three approaches to probability) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.प्रायिकता की परिभाषा के लिए विभिन्न दृष्टिकोण क्या हैं? (What are different approaches to the definition of probability?):
उत्तर:प्रायिकता सिद्धांत की कई परिभाषाएँ हैं-गणितीय या शास्त्रीय (mathematical or classical),सापेक्ष या अनुभवजन्य (relative or empirical) और कुल प्रायिकता का प्रमेय (theorem of total probability)।
प्रश्न:2.प्रायिकता सिद्धांत में कितने दृष्टिकोण हैं? (How many approaches are there in probability theory?):
उत्तर:इस लेख में,मैं प्रायिकता के तीन दृष्टिकोण प्रस्तुत करने जा रहा हूँ,जो उस अवधारणा की अलग-अलग व्याख्याएँ और शुरू करने के लिए अलग-अलग धारणाएँ प्रदान करते हैं।वे दृष्टिकोण हैं: शास्त्रीय दृष्टिकोण (Classical approach)। आवृत्ति-आधारित (या अनुभवजन्य) दृष्टिकोण (Frequency-based (or empirical))।व्यक्तिपरक दृष्टिकोण (subjective approach)।
प्रश्न:3.प्रायिकता के चार प्रकार क्या हैं? (What are the four types of probability?):
उत्तर:प्रायिकता पर चार दृष्टिकोण आमतौर पर उपयोग किए जाते हैं: शास्त्रीय (Classical),अनुभवजन्य (Empirical),व्यक्तिपरक (आत्मनिष्ठ) (Subjective) और स्वयंसिद्ध (Axiomatic)।
शास्त्रीय (कभी-कभी “एक प्राथमिकता (A posteriori)” या “सैद्धांतिक (Frequentist)” कहा जाता है)
अनुभवजन्य (कभी-कभी “ए पोस्टीरियरी (A posteriori”या “फ़्रीक्वेंटिस्ट (“Frequentist”) कहा जाता है)
आत्मनिष्ठ (विषयपरक) (Subjective)।
स्वयंसिद्ध। (Axiomatic)
प्रश्न:4.प्रायिकता के दो दृष्टिकोण क्या हैं? (What are the two approaches to probability?):
उत्तर:घटनाओं की संभावनाओं को निर्दिष्ट करने के तीन तरीके हैं:शास्त्रीय दृष्टिकोण,सापेक्ष-आवृत्ति दृष्टिकोण (frequency approach, subjective approach),व्यक्तिपरक दृष्टिकोण (subjective approach)।विवरण यदि किसी प्रयोग के n सरल परिणाम हैं,तो यह विधि प्रत्येक परिणाम के लिए 1/n की प्रायिकता निर्दिष्ट करेगी।
प्रश्न:5.प्रायिकता में शास्त्रीय दृष्टिकोण क्या है? (What is classical approach in probability?):
उत्तर:प्रायिकता के लिए शास्त्रीय दृष्टिकोण कुल संभावित परिणामों की संख्या के लिए क्रमिक परीक्षणों की एक श्रृंखला में अनुकूल परिणामों की संख्या के अनुपात के रूप में संभाव्यता व्यक्त करता है।इसके अलावा,सभी संभावित परिणामों को समान रूप से संभवतः माना जाता है और कोई भी दो संभावित परिणाम एक ही परीक्षण से परिणाम नहीं हो सकते हैं।
प्रश्न:6.प्रायिकता के इस दृष्टिकोण को क्या कहा जाता है? (What is this approach to probability called?):
उत्तर:विषय कलन (Calculus)।
प्रश्न:7.प्रायिकता किस क्षेत्र में लागू होती है? (In which field the probability is applicable?):
उत्तर;सांख्यिकी (statistics),वित्त (finance),जुआ (gambling) कृत्रिम बुद्धि (artificial intelligence),मशीन सीखने (machine learning),कंप्यूटर विज्ञान (computer science),खेल सिद्धांत (game theory) और दर्शन (philosophy) जैसे अध्ययनों के क्षेत्र में प्रायिकता सिद्धांत का व्यापक रूप से उपयोग किया जाता है।
प्रश्न:8.संभाव्यता के 5 नियम क्या हैं? (What are the 5 rules of probability?):
उत्तर:प्रायिकता नियम
1.जोड़ नियम (The Addition Rule): P(A or B) =P(A) +P(B)-P(A और B)
2.गुणन नियम (Multiplication Rule): P(A and B) = P(A)*P(B|A) or P(B) * P(A|B)
3.पूरक नियम (The Complement Rule): P(not A) = 1-P(A)
4.कुल प्रायिकता का नियम (Law of Total Probability): P(A) = P(A|B)*P(B) +P(A|not B) *P(not B)
प्रश्न:9.प्रायिकता का क्या अर्थ है? (What does probability mean?)
उत्तर:1:संभावित होने की अवस्था या भाव।2: कुछ (जैसे कोई घटना या परिस्थिति) जो संभावित हो।3a(1): समान रूप से संभावित परिणामों के एक संपूर्ण सेट में परिणामों की संख्या का अनुपात जो किसी दिए गए ईवेंट को संभावित परिणामों की कुल संख्या से उत्पन्न करता है।
प्रश्न:10.शास्त्रीय दृष्टिकोण क्या है? (What is the classical approach?):
उत्तर:शास्त्रीय दृष्टिकोण (Classical approach) विचार का सबसे पुराना
औपचारिक स्कूल है जो 1900 के आसपास शुरू हुआ और 1920 के दशक में जारी रहा।यह मुख्य रूप से प्रबंधन प्रथाओं के आधार पर श्रमिकों और संगठनों की दक्षता बढ़ाने से संबंधित है,जो सावधानीपूर्वक अवलोकन का परिणाम था।
प्रश्न:11.प्रायिकता के लिए स्वयंसिद्ध दृष्टिकोण क्या है? (What is axiomatic approach to probability?):
उत्तर:स्वयंसिद्ध प्रायिकता (Axiomatic Probability) किसी घटना की प्रायिकता का वर्णन करने का एक और तरीका है।जैसा कि शब्द ही कहता है,इस दृष्टिकोण में,संभावनाओं को निर्दिष्ट करने से पहले कुछ स्वयंसिद्ध पूर्वनिर्धारित होते हैं।यह घटना की मात्रा निर्धारित करने के लिए किया जाता है और इसलिए घटना की घटना (occurrence) या गैर-घटना (non-occurrence) की गणना को आसान बनाने के लिए किया जाता है।
प्रश्न:12.शास्त्रीय दृष्टिकोण के प्रमुख प्रकार क्या हैं? (What are the major types of classical approaches?):
उत्तर:शास्त्रीय दृष्टिकोण (classical approach) ने तर्कसंगतता (rationality) और संगठनों और श्रमिकों को यथासंभव कुशल बनाने पर जोर दिया।दो प्रमुख सिद्धांतों में शास्त्रीय (classical approach) दृष्टिकोण शामिल है:वैज्ञानिक प्रबंधन (scientific management) और सामान्य प्रशासनिक (general administrative)।परिभाषा (2):शास्त्रीय दृष्टिकोण (classical approach) को प्रबंधन प्रक्रिया (Management Process),कार्यात्मक (Functional) और अनुभवजन्य दृष्टिकोण (Empirical Approach) भी कहा जाता है।
प्रश्न:13.शास्त्रीय दृष्टिकोण के पीछे मुख्य विचार क्या है? (What is the main idea behind classical approach?):
उत्तर:शास्त्रीय प्रबंधन सिद्धांत इस विश्वास पर आधारित है कि श्रमिकों की केवल शारीरिक और आर्थिक जरूरतें होती हैं।यह सामाजिक जरूरतों या नौकरी की संतुष्टि को ध्यान में नहीं रखता है बल्कि इसके बजाय श्रम की विशेषज्ञता,केंद्रीकृत नेतृत्व और निर्णय लेने और लाभ को अधिकतम करने की वकालत करता है।
प्रश्न:14.सिस्टम दृष्टिकोण क्या है? (What is system approach?):
उत्तर:सिस्टम दृष्टिकोण एक पुरानी अवधारणा है। दृष्टिकोण इस धारणा पर खड़ा है कि एक जटिल अवधारणा को सरल समझने में आसान इकाइयों में तोड़ने से जटिलता को बेहतर ढंग से समझने में मदद मिलती है।लुडविग वॉन बर्टलान्फी (Ludwig von Bertalanffy) ने सबसे पहले ‘सामान्य प्रणाली’ के नाम से सिस्टम दृष्टिकोण का प्रस्ताव रखा।
प्रश्न:15.शास्त्रीय दृष्टिकोण की विशेषताएं क्या हैं? (What are the features of classical approach?):
उत्तर;शास्त्रीय दृष्टिकोण निम्नलिखित विशेषताओं को दर्शाता है:
(1.)शास्त्रीय सिद्धांत श्रम विभाजन (division of labour) ,विशेषज्ञता (specialization),संरचना (structure),अदिश (scalar),कार्यात्मक प्रक्रियाओं )(functional processes) और नियंत्रण की अवधि (span of control) के माध्यम से औपचारिक संगठन की शारीरिक रचना पर केंद्रित है।(2.)प्रबंधन:प्रबंधकीय अनुभवों का अध्ययन है।
प्रश्न:16.सिस्टम दृष्टिकोण के चरण क्या हैं? (What are the steps of system approach?):
उत्तर:आउटपुट निर्दिष्ट करना (Specifying the Output)।
मूल्यांकन प्रक्रिया की तैयारी (Preparation of Evaluation Procedure)।
इनपुट विनिर्देशों की पहचान करना (Identifying Input Specifications)।
प्रक्रिया विकल्पों को डिजाइन करना (Designing the Process Alternatives)।
सर्वश्रेष्ठ विकल्प का चयन (Selection of the Best Alternative)।
सीखने के अनुभवों की योजना बनाना (Planning for Learning Experiences)।
परीक्षण (Tryout)।
प्रणाली का संशोधन और कार्यान्वयन (Revision and Implementation of the System)।
प्रश्न:17.आधुनिक दृष्टिकोण क्या है? (What is modern approach?):
उत्तर:आधुनिक दृष्टिकोण तथ्य आधारित है और वैज्ञानिक और निश्चित निष्कर्ष पर पहुंचने के लिए राजनीतिक घटना के तथ्यात्मक अध्ययन पर जोर देता है।आज राजनीतिक वैज्ञानिक यह विश्लेषण करने में अधिक रुचि रखते हैं कि लोग राज्य और सरकार से संबंधित मामलों में कैसे व्यवहार करते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा प्रायिकता के लिए तीन दृष्टिकोण (Three approaches to probability) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
