Analytic Continuation
1.विश्लेषिक-सांतत्य (Analytic Continuation),सम्मिश्र विश्लेषण में विश्लेषिक-सांतत्य (Analytic Continuation in Complex Analysis):
विश्लेषिक-सांतत्य (Analytic Continuation) के इस आर्टिकल में विश्लेषिक फलन के प्रान्त को विस्तृत करके पुनः उस प्रान्त में उचित विश्लेषिक फलन परिभाषित करने जैसी समस्याओं का अध्ययन करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Topological Preliminaries
2.विश्लेषिक-सांतत्य के साधित उदाहरण (Analytic Continuation Solved Illustrations):
Illustration:3.सिद्ध कीजिए कि श्रेणियों (Prove that the functions defined by the series)
1+a z+a^2 z^2+\ldots तथा (and) \frac{1}{1-z}-\frac{(1-a)z}{(1-z)^2}+\frac{(1-a)^2 z^2}{(1-z)^3}-\ldots \ldots
द्वारा परिभाषित फलन एक दूसरे के विश्लेषिक सांतत्य हैं।
(are analytic continuation of each other.)
Solution:घात श्रेणी 1+a z+a^2 z^2+\ldots फलन \frac{1}{1-a z} को प्रदर्शित करता है जो |z|=\frac{1}{|a|} इसका अभिसरण वृत्त है,इसकी केवल विचित्रता है z=\frac{1}{a},(a>0)
पुनः श्रेणी \frac{1}{1-z}-\frac{(1-a) z}{(1-z)^2}+\frac{(1-a)^2 z^2}{(1-z)^3} - \ldots \ldots \cdots(2)
फलन \frac{1}{1-z} \cdot \frac{1}{1+\frac{(1-a) z}{1-z}}=\frac{1}{1-a z} को प्रदर्शित करता है
दिया है \left|\frac{(1-a) z}{1-z}\right|<1 यदि a वास्तविक है
तब \left|\frac{(1-a) z}{1-z}\right|=1 से
\Rightarrow(1-z)(1-\bar{z})=(1-a)^2 z \bar{z} \\ \Rightarrow 1-(z+\bar{z})+z \bar{z}=(1-a)^2 z \bar{z} \\ \Rightarrow a(2-a) z\bar{z}-(z+\bar{z})+1=0 \\ z \bar{z}=x^2+y^2 तथा z+\bar{z}=2 x \\ \Rightarrow x^2+y^2-\frac{2x}{a(2-a)}+\frac{1}{a(2-a)}=0 \\ \Rightarrow\left(x-\frac{1}{a(2-a)}\right)^2 +y^2 =\left(\frac{1-a}{a(2-a)}\right)^2 \cdots(3)
जो कि वृत्त है जिसका केन्द्र \left(\frac{1}{a(2-a)}, 0\right) तथा त्रिज्या \frac{1-a}{a(2-a)} है।
द्वितीय श्रेणी का (3) अभिसरण वृत्त है।
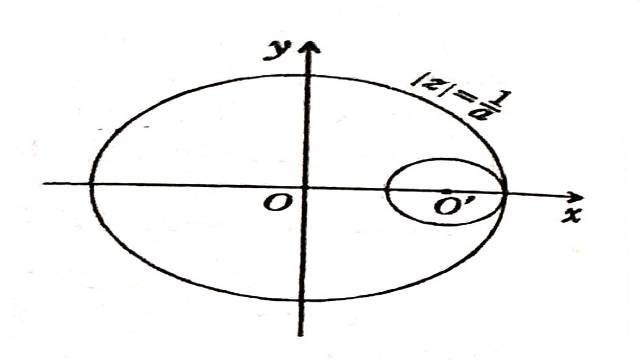
स्थिति:I.माना 0<a<1, इस स्थिति में,वृत्त, (3) वृत्त |z|=\frac{1}{a} को आन्तरिक रूप से स्पर्श करता है जबकि दोनों वृतों कि केंद्रों के बीच दूरी उनकी के अंतर के बराबर है ।अतः फलन वृत |z|=\frac{1}{a} के बाहर संतत नहीं है इस वृत कि प्राकृतिक सीमा नहीं है ।
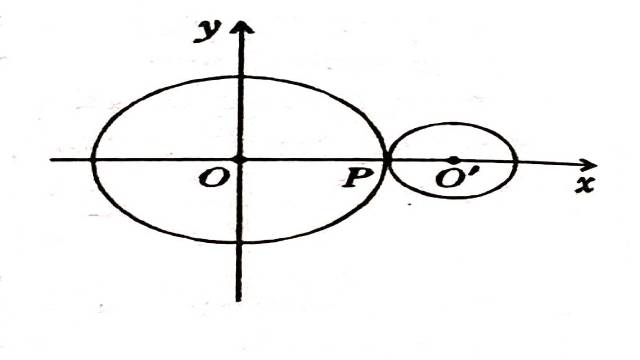
स्थिति:II.माना 1<a<2, इस स्थिति में दोनों वृत्त |z|=\frac{1}{a} को बाहय रूप से स्पर्श करता है। इसलिए अभिसरण का कोई उभयनिष्ट क्षेत्र नहीं है यधपि वे समान फलन \frac{1}{(1-az)} के विश्लेषिक सांतत्य हैं।
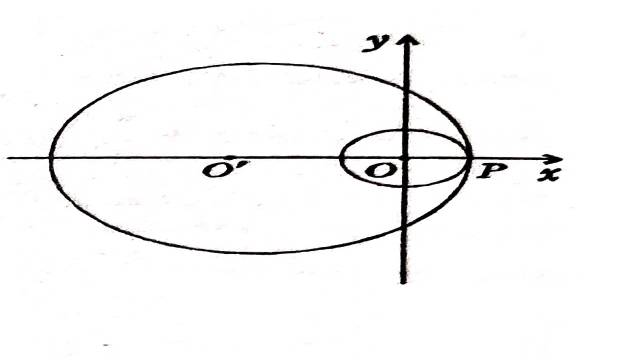
स्थिति:III.माना a>2, इस स्थिति में,वृत्त |z|=\frac{1}{a}, (3) को आन्तरिक रूप से स्पर्श करता है। अतः द्वितीय श्रेणी,प्रथम वृत्त,(3) के आन्तरिक भाग तथा क्षेत्र |z|<\frac{1}{a} उभयनिष्ठ भाग में प्रथम श्रेणी का विश्लेषिक सांतत्य है।
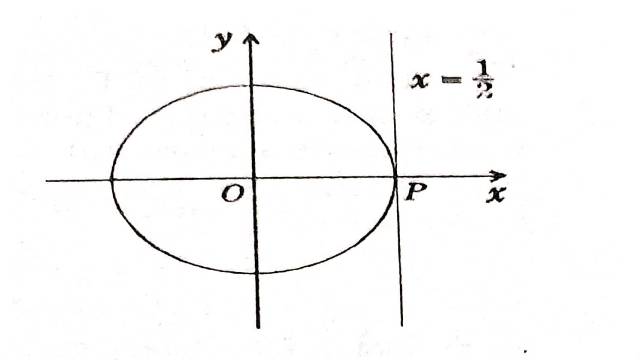
स्थिति:IV.माना a=2 यहाँ श्रेणी (1) वृत्त |z|=\frac{1}{a} के अन्दर फलन \frac{1}{(1-2z)} को प्रदर्शित करती है।श्रेणी (2) उसी फलन \left(\frac{1}{1-2 z}\right),क्षेत्र \left|\frac{z}{1-z}\right|<1 में परिभाषित है
i.e. z \bar{z}<(1-z)(1-\bar{z}) \\ \Rightarrow x<\frac{1}{2}
इस प्रकार श्रेणी (2) अर्ध-समतल x<\frac{1}{2} में फलन \left(\frac{1}{1-2 z}\right) को प्रदर्शित करती है।यहाँ ध्यान दें कि रेखा x=\frac{1}{2},वृत्त को स्पर्श करती है।
अतः इस स्थिति में श्रेणी (2),श्रेणी (1) का विश्लेषिक सांतत्य है क्षेत्र |z|<\frac{1}{2} ,अर्ध-समतल x<\frac{1}{2}
स्थिति:V.यदि a=1 तो द्वितीय श्रेणी \frac{1}{1-z} में परिवर्तित हो जाती है और प्रथम श्रेणी 1+z+z^2+\ldots जो फलन \frac{1}{1-z} को प्रदर्शित करती है।
Illustration:4.सिद्ध कीजिए कि घात श्रेणी \overset{\infty}{\underset{n=0}{\sum}} z^{n!} का अभिसरण वृत्त श्रेणी के योग फलन की स्वाभाविक सीमा भी है।
(Show that the circle of convergence of the power series \overset{\infty}{\underset{n=0}{\sum}} z^{n!} is also the natural boundary for its sum function.)
Solution: \sum u_n(z)=f(z)= \overset{\infty}{\underset{n=1}{\sum}} z^{n!} \\ \therefore \underset{n=\infty}{Lt} \frac{u_n}{u_{n+1}}=Lt \frac{z^{n!}}{z^{(n+1)!}} \\ =Lt. \frac{1}{z^{n+1}} \rightarrow \infty i.e. >1
यदि |z|<1
अतः श्रेणी \sum u_n(z) अभिसारी है यदि |z|<1
इसलिए अभिसरण वृत्त |z|=1 के अन्दर है जिसकी श्रेणी अभिसारी है।
f(z)=\overset{\infty}{\underset{n=1}{\sum}} z^{n!} \\ =\sum_{n=1}^q z^{n!}+\overset{\infty}{\underset{n=q+1}{\sum}} z^{n!} \\ =f_1(z)+f_2(z)
यदि बिन्दु P लें,अभिसरण वृत्त के बाहर z=r e^{\frac{2 \pi i p}{q!}}, r>1
जहाँ p तथा q पूर्णांक हैं।
हम f(z) के व्यवहार का परीक्षण करेंगे जब P अभिसरण वृत्त की ओर ध्रुवान्तर रेखा के सहारे अग्रसर होता है
z^{n!}=\left[r \cdot e^{\frac{2 \pi i p}{q!}}\right]^{n!} \\ =r^{n!} \cdot e^{\frac{2 \pi i p n!}{q!}}
अब q! , n! का भाजक है इसलिए \frac{n!}{q!} पूर्णांक है तथा हम जानते हैं कि
e^{2 \pi i k}=1 \\ f_1(z)=\overset{q}{\underset{n=0}{\sum}} r^{n!} P पर
f_1(z) ,r की q! घात का बहुपद है और r \rightarrow 1 अद्वितीय सीमा की ओर अग्रसर है
f_2(z)=\overset{\infty}{\underset{n=q+1}{\sum}} r^{n!} \rightarrow \infty जब \rightarrow 1 \\ f(z)=f_1(z)+f_2(z) \rightarrow \infty जब 0 \rightarrow 1
अतः बिन्दु e^{\frac{2 \pi i p}{q!}} अभिसरण वृत्त |z| पर f(z) की विचित्रता है।दूसरी ओर छोटे वृत्त |z|=1 पर e^{\frac{2 \pi i p}{q!}} स्थित जहाँ p पूर्णांक है।
स्पष्ट है कि अभिसरण वृत्त को प्रतिच्छेद करने वाला प्रत्येक वृत्त इस रूप के बिन्दुओं को रखेगा।परिणामस्वरूप |z|=1 के बाहर,f(z) विश्लेषिक सांतत्य नहीं है।अतः |z|=1 की सीमा प्राकृतिक सीमा है।
Illustration:5.सिद्ध कीजिए कि फलन f_1(z)=\int_0^{\infty} t^3 e^{-z t} \cdot d t क्षेत्र Re(z)>0 में विश्लेषिक है।फलन ज्ञात कीजिए जो का विश्लेषिक सांतत्य हो।
(Prove that the function defined by f_1(z)=\int_0^{\infty} t^3 e^{-z t} \cdot dt is analytic at all points for which Re(z).)
Solution: f_1(z)=\int_0^{\infty} t^3 e^{-z t} \cdot d t
खण्डशः समाकलन करने पर:
f_1(z)=\left[t^3\left(\frac{e^{-z t}}{-z}\right)-3 t^2\left(\frac{e^{-z t}}{z^2}\right)+6 t\left(\frac{e^{-z t}}{-z^3}\right)-6\left(\frac{e^{-z t}}{z^4}\right)\right]_0^{\infty} \\=\frac{6}{z^4}
यद्यपि Re(z)>0
माना f_2(z)=\frac{6}{z^4}
तब f_1(z)=f_2(z),Re(z)>0 के लिए
z=0 के अतिरिक्त सम्मिश्र समतल में फलन f_2(z) विश्लेषिक है।
f_1(z)=f_2(z) \quad \forall z प्रत्येक Re(z)>0 के लिए
अतः f_2(z) , f_1(z) का अभीष्ट विश्लेषिक सांतत्य प्रदर्शित करता है।
Illustration:6.सिद्ध कीजिए कि घात श्रेणी \overset{\infty}{\underset{n=0}{\sum}} z^{3 n} की वृत्त |z|=1 से आगे विश्लेषिक सांतत्य नहीं किया जा सकता।
(Show that the power series \overset{\infty}{\underset{n=0}{\sum}} z^{3 n} can not be continued analytically beyond the circle |z|=1 .)
Solution: u_n(z)=z^{3 n} \\ \therefore\left|u_n(z)\right|^{\frac{1}{n}}=\left|z^{3 n}\right|^{\frac{1}{n}} \\ =\left|z^3\right| \\ =|z|^3
अतः श्रेणी \sum u_n(z) अभिसारी है यदि |z| <1
अभिसरण वृत्त |z|=1 \\ f(z)=\overset{q-1}{\underset{n=0}{\sum}} z^{3 n}+ \overset{\infty}{\underset{n=q}{\sum}} z^{3 n} \\ =f_1(z)+f_2(z)
यदि बिन्दु P , |z|=1 अभिसरण वृत्त के बाहर लें
जहाँ r>1 तथा p,q पूर्णांक हैं।
\left(z=r e^{\frac{2 \pi i p}{3^q}} \right) \\ z^{3 n}=\left[r e^{\frac{ 2 \pi i p}{3^q}}\right]^{3n} \\ =r^{3 n} e^{\frac{2 \pi i p 3^n}{3^q}}
यदि n>q \Rightarrow 2^{n-q} सम है इसलिए e^{\frac{2 \pi i p 3^n}{3^q}}, e^{2 \pi i k}=1 रूप का है।
f_1(z)=\overset{q-1}{\underset{n=0}{\sum}} z^{3 n} \\ f_1(z)=\overset{q-1}{\underset{n=1}{\sum}} z^{3 n}, P पर
बहुपद f_1(z) ,r की घात 3^q का में है तथा अद्वितीय सीमा की ओर अग्रसर है जब r \rightarrow 1 \\ f_2(z)= \overset{\infty}{\underset{n=q}{\sum}} z^{3 n} \rightarrow \infty
जब r \rightarrow 1 \\ f(z)=f_1(z)+f_2(z) \rightarrow \infty जब z \rightarrow 1
इसलिए अभिसरण वृत्त |z|=1 पर बिन्दु e^{\frac{ 2 \pi i p}{3^q}} ,f(z) की विचित्रता है।दूसरी ओर छोटे वृत्त |z|=1 पर e^{\frac{ 2 \pi i p}{3^q}} स्थित जहाँ p पूर्णांक है।
स्पष्ट है कि अभिसरण वृत्त को प्रतिच्छेद करने वाला प्रत्येक वृत्त इस रूप के बिन्दुओं को रखेगा।परिणामस्वरूप |z|=1 के बाहर,f(z) विश्लेषिक सांतत्य नहीं है।अतः |z|=1 की सीमा प्राकृतिक सीमा है।
उपर्युक्त उदाहरणों के द्वारा विश्लेषिक-सांतत्य (Analytic Continuation),सम्मिश्र विश्लेषण में विश्लेषिक-सांतत्य (Analytic Continuation in Complex Analysis) को समझ सकते हैं।
Also Read This Article:- Complex Number in Complex Analysis
3.विश्लेषिक-सांतत्य (Frequently Asked Questions Related to Analytic Continuation),सम्मिश्र विश्लेषण में विश्लेषिक-सांतत्य (Analytic Continuation in Complex Analysis) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.फलन एवं श्रृंखला अवयव से क्या तात्पर्य है? (What Do You Mean by Function Element and Chain?):
उत्तर:समुच्चय {f(z),G} ;जिसमें G प्रान्त है तथा f(z) उस प्रान्त पर परिभाषित एकमानी वैश्लेषिक फलन है,फलन अवयव कहलाता है।दो फलन अवयव \left\{f_1(z), G_1\right\} तथा \left\{f_2(z), G_2\right\} बराबर हैं यदि और केवल यदि G_{1}=G_2, f_1(z)=f_2(z)
प्रश्न:2.विश्लेषिक सांतत्य पर संक्षिप्त टिप्पणी लिखो। (Write a Short Note on Analytic Continuation):
उत्तर:विश्लेषिक फलन के शून्य सिद्धान्त से हम जानते हैं कि f_1(z) तथा f_2(z) किसी प्रान्त G में दो विश्लेषिक फलन इस प्रकार से है कि
(a)G के किसी बिन्दु z_0 के प्रतिवेश,चाहे जितना भी छोटा है,में संपाती है,या
(b)केवल किसी पथ या खण्ड चाहे जितना भी छोटा है,और जो G के किसी बिन्दु पर समाप्त हो,के अनुदिश विश्लेषिक हो,या
(c)केवल अनन्त विभिन्न बिन्दुओं जिनका सीमा बिन्दु प्रान्त G का z_0 है,पर विश्लेषिक हो,
तो G में दोनों फलन सर्वसम (identical) होंगे।अतः प्रान्त G में परिभाषित विश्लेषिक फलन को इस प्रकार के बिन्दुओं के समुच्चय पर प्राप्त मानों से ज्ञात किया जा सकता है।
अब माना कि f_1(z) तथा f_2(z) कोई दो फलन इस प्रकार से दिए हुए हैं कि ये क्रमशः प्रान्त G_1 एवं G_2 में विश्लेषिक है।पुनः यह भी माना कि G_1 एवं G_2 का उभयनिष्ठ प्रान्त G_1 \cap G_2 है ताकि अनन्त बिन्दुओं के समुच्चय जिनका सीमा बिन्दु G_1 \cap G_2 में है,पर f_1(z)=f_2(z) स्पष्ट है कि पूरे क्षेत्र G_1 \cap G_2 में f_1(z)=f_2(z) होगा।अतः फलन f_1 तथा f_2 एक दूसरे को अद्वितीय रूप से निर्धारित करते हैं।दूसरे शब्दों में f_1(z) के अतिरिक्त कोई भी फलन G_1 में विश्लेषिक नहीं हो सकता है जो कि G_1 \cap G_2 में समान मान रखता हो।इसी प्रकार f_2(z) के अतिरिक्त कोई भी फलन G_2 में विश्लेषिक नहीं हो सकता जो कि G_1 \cap G_2 में समान मान रखता हो।यदि G_1 एवं G_2 कोई दो प्रान्त हैं ताकि G_1 \cap G_2 उपर्युक्त प्रतिबन्धों को सन्तुष्ट करता है एवं यदि f_1(z) प्रान्त G_1 में विश्लेषिक फलन हो,तो या तो कोई भी फलन नहीं होगा या केवल एक फलन f_2(z) प्रान्त G_2 में होगा जो कि G_1 \cap G_2 में f_1(z) के संपाती होगा।यदि इस प्रकार कोई फलन f_2(z) का अस्तित्व हो,तो f_2(z) ,प्रान्त G_1 में परिभाषानुसार फलन f_1(z) का प्रान्त G_1 से G_2 में विश्लेषिक कहा जाता है।इसी प्रकार f_2(z) को f_1(z) का प्रान्त में विश्लेषिक सांतत्य कहा जाता है।वास्तव में f_1(z) एवं f_2(z) एक दूसरे के विश्लेषिक सांतत्य हैं।
प्रश्न:3.सीधा विश्लेषिक सांतत्य की परिभाषा दीजिए। (Define Direct Analytic Continuation):

उत्तर:मान लें \left\{f_1(z), G_1\right\} तथा \left\{f_2(z), G_2\right\} दो फलन अवयव हैं।एक फलन अवयव को दूसरे फलन अवयव का सीधा विश्लेषिक सांतत्य कहते हैं यदि G_1 \cap G_2 \neq \phi तथा यदि प्रान्त G_1 \cap G_2 में f_1=f_2।प्रतीकात्मक भाषा में इस तथ्य को \left\{f_1(z), G_1\right\} \sim \left\{f_2(z), G_2\right\} या सरल रूप में
\left( f_1,G_1\right) \sim \left( f_2,G_2\right)
द्वारा व्यक्त करते हैं।
माना कि f_1(z) प्रान्त G_1 में विश्लेषिक फलन है तथा दूसरा फलन f_2 (z) प्रान्त G_2 में विश्लेषिक है। G_1 एवं G_{22} का उभयनिष्ठ प्रान्त G_{12} है।यदि G_{12} में f_1(z)=f_2(z) हों,तो f_1(z) का G_1 से G_2 में G_{12} का विश्लेषिक सांतत्य है।हम इसे सीधा विश्लेषिक सांतत्य भी कह सकते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा विश्लेषिक-सांतत्य (Analytic Continuation),सम्मिश्र विश्लेषण में विश्लेषिक-सांतत्य (Analytic Continuation in Complex Analysis) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Analytic Continuation
विश्लेषिक-सांतत्य (Analytic Continuation)
Analytic Continuation
विश्लेषिक-सांतत्य (Analytic Continuation) के इस आर्टिकल में विश्लेषिक फलन के प्रान्त
को विस्तृत करके पुनः उस प्रान्त में उचित विश्लेषिक फलन परिभाषित करने जैसी
समस्याओं का अध्ययन करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.