Equation of Enveloping Cylinder
1.अन्वालोपी बेलन का समीकरण (Equation of Enveloping Cylinder),अन्वालोपी बेलन (Enveloping Cylinder):
अन्वालोपी बेलन का समीकरण (Equation of Enveloping Cylinder) ज्ञात करने के लिए जनक रेखा तथा निर्देशक वक्र का समीकरण ज्ञात होना चाहिए।
अन्वालोपी बेलन का समीकरण (Equation of Enveloping Cylinder):
गोले x^{2}+y^{2}+z^{2}=a^{2} के अन्वालोपी बेलन का समीकरण ज्ञात करना जिसकी जनक रेखाएँ \frac{x}{l}=\frac{y}{m}=\frac{z}{n} के समान्तर हैं:
(To find the enveloping cylinder x^{2}+y^{2}+z^{2}=a^{2} of the sphere whose generators are parallel to the line \frac{x}{l}=\frac{y}{m}=\frac{z}{n}):
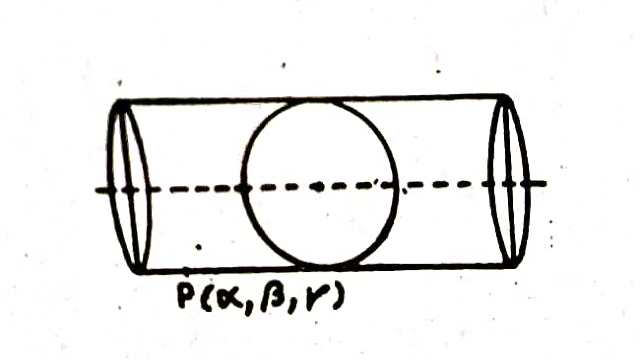
माना कि P(\alpha, \beta, \gamma) बेलन पर कोई बिन्दु है तो P से होकर जाने वाले जनक के समीकरण निम्न होंगे:
\frac{x-\alpha}{x}=\frac{y-\beta}{m}=\frac{z-n}{n}=r \ldots(1)(माना)
इस सरल रेखा पर स्थित कोई भी बिन्दु के निर्देशांक होंगे:
(l r+\alpha, m r+\beta, n r+\gamma)
यह बिन्दु गोले पर स्थित होगा यदि:
(l r+\alpha)^{2}+(m r+\beta)^{2}+(n r+\gamma)^{2}=a^{2} \\ \Rightarrow \left(l^{2}+m^{2}+ n^{2}\right) r^{2}+2 r(l \alpha+m \beta+n \gamma)+\left(\alpha^{2}+\beta^{2}+\gamma^{2}-a^{2}\right)=0 \ldots(2)
रेखा (1) गोले को स्पर्श करेगी यदि समीकरण (2) के मूल संपाती हों अर्थात्
4(l \alpha+m \beta+n \gamma)^{2}= 4\left(l^{2}+m^{2}+n^{2}\right) \left(\alpha^{2}+ \beta^{2}+\gamma^{2}-a^{2}\right)
अतः बिन्दु P का बिन्दुपथ होगा:
(l x+m y+n z)^{2}=\left(l^{2}+m^{2}+n^{2}\right)\left(x^{2}+y^{2}+z^{2}-a^{2}\right)
जो कि अन्वालोपी बेलन का अभीष्ट समीकरण है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Equation of Cylinder 3D
2.अन्वालोपी बेलन का समीकरण के उदाहरण (Equation of Enveloping Cylinder Examples):
Example:1.गोले x^{2}+y^{2}+z^{2}-2 x+4 y-1=0 के उस अन्वालोपी बेलन का समीकरण ज्ञात कीजिए जिसके जनक x=y=z रेखा के समान्तर हैं।इसकी निर्देशक वक्र भी ज्ञात करो।
(Find the enveloping cylinder of the sphere x^{2}+y^{2}+z^{2}-2 x+4 y-1=0 having its generators parallel to x=y=z.Also find its guiding curve.)
Solution:माना कि अभीष्ट बेलन पर P(\alpha, \beta, \gamma) कोई बिन्दु है।अब P से गुजरने वाली तथा \frac{x}{1}=\frac{y}{1}=\frac{z}{1} के समान्तर जनक रेखा का समीकरण होगा:
\frac{x-\alpha}{1}=\frac{y-\beta}{1}=\frac{z-\gamma}{1}=r \ldots(1) (माना)
इस रेखा पर किसी बिन्दु के निर्देशांक होंगे: (r+\alpha, r+\beta, r+\gamma)
यह बिन्दु गोले पर स्थित होगा यदि:
\Rightarrow(r+\alpha)^{2}+(r+\beta)^{2}+\left(r+\gamma\right)^{2}- 2 (r+\alpha) +4(r+\beta)-1=0 \\ \Rightarrow r^{2}+2 r \alpha+\alpha^{2}+r^{2}+2 r \beta+\beta^{2} +r^{2}+2 r \gamma+\gamma^{2}-2 r-2 \alpha +4 r+4 \beta-1=0 \\ \Rightarrow 3 r^{2}+2 r(\alpha+\beta+\gamma+1)+ \alpha^{2}+\beta^{2}+\gamma^{2}-2 \alpha+4 \beta-1=0 \ldots(2)
रेखा (1) गोले को स्पर्श करेगी यदि समीकरण (2) के मूल संपाती हों अर्थात्
B^{2}-4 A C=0 \\ 4\left(\alpha+\beta+\gamma+1\right)^{2}-4 \times 3 \times\left(\alpha^{2}+ \beta^{2} +\gamma^{2}-2 \alpha+4 \beta-1\right)=0 \\ \Rightarrow(\alpha+\beta+ \gamma+1)^{2} -3\left(\alpha^{2}+\beta^{2}+\gamma^{2}-2 \alpha+4 \beta-1\right)=0 \\ \Rightarrow \alpha^{2}+ \beta^{2} +\gamma^{2}+2 \alpha \gamma+2 \alpha+2 \beta \gamma+2 \beta+2 \gamma+1-3 \alpha^{2}-3 \beta^{2}-3 \gamma^{2}+6 \alpha -12 \beta+3+2 \alpha \beta=0 \\ \Rightarrow-2 \alpha^{2}-2 \beta^{2}-2 \gamma^{2}+2 \alpha \gamma+2 \beta \gamma+2 \alpha \beta+8 \alpha-10 \beta+2 \gamma+4=0 \\ \Rightarrow-2\left(\alpha^{2}+\beta^{2}+\gamma^{2}-\alpha \gamma-\beta \gamma-\alpha \beta-4 \alpha+5 \beta-\gamma-2\right)=0 \\ \Rightarrow \alpha^{2}+\beta^{2}+ \gamma^{2}-\alpha \gamma-\beta \gamma-\alpha \beta-4 \alpha+5 \beta-\gamma-2=0
अतः बिन्दु P का बिन्दुपथ होगा:
x^{2}+y^{2}+z^{2}-x y-y z-z x-4 x+5 y-z-2=0
Example:2.(a,b,c) केन्द्र तथा r त्रिज्या वाले गोले के अन्वालोपी बेलन का समीकरण ज्ञात करो जिसके जनक उस रेखा के समान्तर हैं जिसकी दिक्कोज्याएँ l,m,n हैं।
(Find the equation of a cylinder which envelopes a sphere of centre (a,b,c) and radius r and has its generators parallel to the line whose direction cosines are l,m,n)
Solution:(a,b,c) केन्द्र तथा r त्रिज्या वाले गोले का समीकरण:
(x-a)^{2}+(y-b)^{2}+(z-c)^{2}=r^{2} \\ x^{2}+y^{2}+z^{2}-2 a x-2 b y-2 c z+a^{2}+b^{2}+c^{2}-r^{2}=0 \ldots(1)
माना कि अभीष्ट बेलन पर P(\alpha, \beta, \gamma) कोई बिन्दु है।अब P से गुजरने वाली जनक रेखा का समीकरण होगा:
\frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n}=r \ldots(2)(माना)
इस रेखा पर किसी बिन्दु के निर्देशांक होंगे:
(l r+\alpha, m r+\beta, n r+\gamma)
यह बिन्दु गोले पर स्थित होगा यदि:
(l r+\alpha)^{2}+(m r+\beta)^{2}+(n r+\gamma)^{2}-2 a(l r+\alpha) -2 b(m r+\beta)-2 c(n r+\gamma) +a^{2}+b^{2}+c^{2}-r^{2}=0 \\ \Rightarrow\left(l^{2}+m^{2}+r^{2}\right) r^{2}+2 r(l r+m \beta+n \gamma-a \alpha-b m-c n) +2(\alpha^{2}+\beta^{2}+\gamma^{2}-2 a \alpha-2 b \beta-2c \gamma+ a^{2} +b^{2}+c^{2}-r^{2})=0 \\ \Rightarrow \left(l^{2}+m^{2}+n^{2}\right) r^{2}+2 r[l(\alpha-a)+m(\beta-b)+n(\gamma-c)] +[(\alpha-a)^{2}+(\beta-b)^{2}+(\gamma-c)^{2}-r^{2}]=0 \cdots(3)
रेखा (2) गोले को स्पर्श करेगी यदि समीकरण (3) के मूल संपाती हों अर्थात्
B^{2}-4 A C=0 \\ \left[4 l(\alpha-a)+m(\beta-b)+n(\gamma-c)\right]^{2}=4\left(l^{2}+m^{2} +n^{2}\right) \left[(\alpha-a)^{2}+(\beta-b)^{2}+(\gamma-c)^{2}-r^{2}\right]
अतः बिन्दु P का बिन्दुपथ होगा:
Example:3. a x^{2}+b y^{2}+c z^{2}=1 के अन्वालोपी बेलन का समीकरण ज्ञात कीजिए जिसकी जनक रेखाएँ \frac{x}{l}=\frac{y}{m}=\frac{z}{n} के समान्तर हैं।
Find the equation of the enveloping cylinder of the surface a x^{2}+b y^{2}+c z^{2}=1 and whose generators are parallel to the line \frac{x}{l}=\frac{y}{m}=\frac{z}{n}.
Solution:माना कि अभीष्ट बेलन पर P(\alpha, \beta, \gamma) कोई बिन्दु है।अब P से गुजरने वाली तथा \frac{x}{l}=\frac{y}{m}=\frac{z}{n} के समान्तर जनक रेखा का समीकरण होगा:
\frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n}=r \ldots(1)(माना)
इस रेखा पर किसी बिन्दु के निर्देशांक होंगे: (l r+\alpha, m r+\beta, n r+\gamma)
यह बिन्दु दिए हुए वक्र पर स्थित होगा यदि:
a(l r+\alpha)^{2}+b(m r+\beta)^{2}+c(n r+\gamma)^{2}=1 \\ \left(a l^{2}+b m^{2}+c n^{2}\right) r^{2}+2r(al \alpha+b m \beta+c n \gamma)+a \alpha^{2}+b \beta^{2}+c \gamma^{2}-1=0 \ldots(2)
रेखा (1) दिए हुए वक्र को स्पर्श करेगी यदि समीकरण (2) के मूल संपाती हों अर्थात्
B^{2}-4 A C=0 \\ 4(a l \alpha+b m \beta+c n \gamma)^{2}-4\left(a l^{2}+b m^{2}+c n^{2}\right)\left(a \alpha^{2}+b \beta^{2}+c \gamma^{2}-1\right)=0
अतः बिन्दु P का बिन्दुपथ होगा:
Example:4.प्रदर्शित कीजिए कि शांकवज ax^{2}+by^{2}+cz^{2}=1 के अन्वालोपी बेलन जिनके जनक z-अक्ष के लम्बवत हैं;z=0 को परवलय में मिलते हैं।
(Show that the enveloping cylinder of the conicoid ax^{2}+by^{2}+cz^{2}=1 with generators perpendicular to z-axis meet the plane z=0 in a parabola)
Solution:z-अक्ष की दिक्कोज्याएँ 0,0,1 है।z-अक्ष के लम्बवत् रेखा की दिक्कोज्याएँ l,m,0 हैं।
माना कि अभीष्ट बेलन पर P(\alpha, \beta, \gamma) कोई बिन्दु है।अब P से गुजरने वाले जनक रेखा का समीकरण होगा:
\frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{0}=r \ldots(1)(माना)
इस रेखा पर किसी बिन्दु के निर्देशांक होंगे: (l r+\alpha, m r+\beta, \gamma)
यह बिन्दु शांकवज पर स्थित होगा यदि:
a(l r+\alpha)^{2}+b(m r+\beta)^{2}+c \gamma^{2}=1 \\ (a l^{2}+b m^{2})r^{2}+2 r(al \alpha+b m \beta)+a \alpha^{2}+b \beta^{2}+c \gamma^{2}-1=0 \ldots(2)
रेखा (1) शांकवज को स्पर्श करेगी यदि समीकरण (2) के मूल संपाती हों अर्थात्
B^{2}-4 A C=0 \\ 4(a l \alpha+b m \beta)^{2}-4\left(a l^{2}+b m^{2}\right)\left(a \alpha^{2}+b \beta^{2}+c \gamma^{2}-1\right)=0
अतः बिन्दु P का बिन्दुपथ होगा:
\left(a l^{2}+b m^{2}\right)\left(a x^{2}+b y^{2}+c z^{2}-1\right)=(alx+b m y)^{2}
समतल z=0 पर इसका प्रतिच्छेदन:
(a l x+b m y)^{2}=\left(a l^{2}+b m^{2}\right)\left(a x^{2}+b y^{2}-1\right), z=0 \\ \Rightarrow a^{2} l^{2} x^{2}+b^{2} m^{2} y^{2}+2 a b l m x y=a^{2} l^{2} x^{2}+a b l^{2} y^{2} -a l^{2}+a b m^{2} x^{2}+b^{2} m^{2} y^{2}-b m^{2} ; z=0 \\ \Rightarrow a b\left(m^{2} x^{2}+l^{2} y^{2}-2 l m x y\right)=a l^{2}+b m^{2},z=0 \\ \Rightarrow a b(m x-l y)^{2}=a l^{2}+b m^{2}, z=0
Example:5.सिद्ध कीजिए कि दीर्घवृत्तज \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1 के अन्वालोपी बेलन जिनके जनक रेखा \frac{x}{0}=\frac{y}{\pm \sqrt{\left(a^{2}-b^{2}\right)}}=\frac{z}{c} के समान्तर है, समतल z=0 को वृत्तों में मिलती है।
(Prove that the enveloping cylinder of the ellipsoid \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1 whose generators are parallel to the line \frac{x}{0}=\frac{y}{\pm \sqrt{\left(a^{2}-b^{2}\right)}}=\frac{z}{c} meets the plane z=0 in circles)
Solution:माना कि अभीष्ट बेलन पर P(\alpha, \beta, \gamma) कोई बिन्दु है।अब P से गुजरने वाली तथा \frac{x}{0}=\frac{y}{\pm \sqrt{\left(a^{2}-b^{2}\right)}}=\frac{z}{c} के समान्तर जनक रेखा का समीकरण होगा:
\frac{x-\alpha}{0}=\frac{y-\beta}{\pm \sqrt{\left(a^{2}-b^{2}\right)}}=\frac{z-\gamma}{c}=r \ldots(1)(माना)
इस रेखा पर किसी बिन्दु के निर्देशांक होंगे: \left ( \alpha, \beta \pm r \sqrt{\left(a^{2}-b^{2}\right)},\gamma+cr \right )
यह बिन्दु दीर्घवृत्तज पर स्थित होगा यदि:
\frac{\alpha^{2}}{a^{2}}+\frac{\left\{\beta \pm r\left(a^{2}-b^{2}\right)\right\}^{2}}{b^{2}}+ \frac{(\gamma+c r)^{2}}{c^{2}}=1 \\ \Rightarrow r^{2}\left[\frac{a^{2}-b^{2}}{b^{2}}+\frac{c^{2}}{c^{2}}\right]+2 r\left[\frac{c \gamma}{c^{2}} \pm \frac{\beta \sqrt{\left(a^{2}-b^{2}\right)}}{b^{2}}\right]+\left( \frac{\alpha^{2}}{a^{2}}+\frac{\beta^{2}}{b^{2}}+\frac{\gamma^{2}}{c^{2}}-1\right)=0 \ldots(2)
रेखा (1) दीर्घवृत्तज को स्पर्श करेगी यदि समीकरण (2) के मूल संपाती हों अर्थात्
B^{2}-4 A C=0 \\ 4\left[\frac{\gamma}{c} \pm \frac{\beta \sqrt{(a^{2}-b^{2}}}{b^{2}}\right]^{2}- 4\left[\frac{a^{2}-b^{2}}{b^{2}}+\frac{c^{2}}{c^{2}}\right]\left[\frac{\alpha^{2}}{a^{2}}+\frac{\beta^{2}}{b^{2}}+ \frac{\gamma^{2}}{c^{2}}-1\right]=0\\ \Rightarrow \frac{\gamma^{2}}{c^{2}}+ \frac{\beta^{2} \left(a^{2}-b^{2}\right)}{b^{4}} \pm \frac{2 \beta \gamma \sqrt{\left(a^{2}-b^{2}\right)}}{b^{2} c}= \left(\frac{a^{2}}{b^{2}}\right)\left[\frac{\alpha^{2}}{a^{2}}+\frac{\beta^{2}}{b^{2}}+\frac{\gamma^{2}}{c^{2}}-1\right]
अतः बिन्दु P का बिन्दुपथ होगा:
\frac{z^{2}}{c^{2}}+\frac{y^{2}\left(a^{2}-b^{2}\right)}{b^{4}} \pm \frac{2 y z \sqrt{\left(a^{2}-b^{2}\right)}}{b^{2} c}=\frac{a^{2}}{b^{2}}\left[\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}-1\right]
यह समतल z=0 पर वक्र को मिलता है:
\frac{y^{2}\left(a^{2}-b^{2}\right)}{b^{4}}=\frac{a^{2}}{b^{2}}\left(\frac{x^{2}}{a^{2}}+ \frac{y^{2}}{b^{2}}-1\right), z=0 \\ \Rightarrow \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=\frac{a^{2}}{b^{2}}, z=0 \\ \Rightarrow x^{2}+y^{2}=a^{2}, z=0
उपर्युक्त उदाहरणों के द्वारा अन्वालोपी बेलन का समीकरण (Equation of Enveloping Cylinder),अन्वालोपी बेलन (Enveloping Cylinder) को समझ सकते हैं।
3.अन्वालोपी बेलन का समीकरण के सवाल (Equation of Enveloping Cylinder Questions):
(1.)शांकवज \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1 के अन्वालोपी बेलन का समीकरण ज्ञात करिए जिसकी जनक रेखाएँ उस रेखा के समान्तर हैं जिसकी दिक्कोज्याएँ l,m,n हैं।
(Find the equation of a cylinder which envelopes the conicoid \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1 and whose generators are parallel to the line with dc’s l,m,n .)
उपर्युक्त सवाल को हल करने पर अन्वालोपी बेलन का समीकरण (Equation of Enveloping Cylinder),अन्वालोपी बेलन (Enveloping Cylinder) को ठीक से समझ सकते हैं।
Also Read This Article:-Equation of Right Circular Cone in 3D
4.अन्वालोपी बेलन का समीकरण (Equation of Enveloping Cylinder),अन्वालोपी बेलन (Enveloping Cylinder) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.अन्वालोपी बेलन की परिभाषा दीजिए। (Define Enveloping Cylinder):
उत्तर:किसी दिए हुए पृष्ठ को स्पर्श करनेवाली उन सरल रेखाओं से जनित पृष्ठ को जो किसी दी हुई निश्चित् रेखा के समान्तर रहती है जिनके अक्ष अन्य निर्देशांक अक्षों के समान्तर होते हैं।
प्रश्न:2.जनक रेखा से क्या आशय है? (What is meant by generator line?):
उत्तर:ऐसी चर सरल रेखा अथवा चर सरल रेखाओं का समूह जो बेलन अथवा अन्वालोपी बेलन के पृष्ठ को जनित करती है तथा बेलन के पृष्ठ पर स्थित होती है।
उत्तर:गोले x^{2}+y^{2}+z^{2}=a^{2} के शीर्ष पर अन्वालोपी शंकु का समीकरण:
\left(\alpha x+\beta y+\gamma z-a^{2}\right)^{2}=\left(x^{2}+y^{2}+z^{2}-a^{2}\right)\left(\alpha^{2}+\beta^{2}+\gamma^{2}-a^{2}\right)
यदि शंकु का शीर्ष (lr,mr,nr) है तो उपर्युक्त समीकरण का समानयन होगा:
r^{2}\left(l x+m y+n z-\frac{a^{2}}{r}\right)^{2}=\left(x^{2}+y^{2}+z^{2}-a^{2}\right)\left(l^{2} r^{2}+m^{2} r^{2}+n^{2} r^{2}-a^{2}\right) \\ \Rightarrow \left(l x+m y+n z-\frac{a^{2}}{r}\right)^{2}=\left(x^{2}+y^{2}+z^{2}-a^{2}\right)(l^{2}+m^{2}+n^{2}-\frac{a^{2}}{r^{2}})
यदि r \rightarrow \infty यदि शीर्ष अनन्त दूरी पर स्थित है तब
तब (l x+m y+n z)^{2}=\left(x^{2}+y^{2}+z^{2}-a^{2}\right) \left(l^{2}+ m^{2}+n^{2}\right)
जो कि अन्वालोपी बेलन का समीकरण है:
उपर्युक्त प्रश्नों के उत्तर द्वारा अन्वालोपी बेलन का समीकरण (Equation of Enveloping Cylinder),अन्वालोपी बेलन (Enveloping Cylinder) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Equation of Enveloping Cylinder
अन्वालोपी बेलन का समीकरण
(Equation of Enveloping Cylinder)
Equation of Enveloping Cylinder
अन्वालोपी बेलन का समीकरण (Equation of Enveloping Cylinder) ज्ञात करने
के लिए जनक रेखा तथा निर्देशक वक्र का समीकरण ज्ञात होना चाहिए।
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
