Linear Programming in Class 12
1.कक्षा 12 में रैखिक प्रोग्रामन (Linear Programming in Class 12),रैखिक प्रोग्रामन (Linear Programming):
कक्षा 12 में रैखिक प्रोग्रामन (Linear Programming in Class 12) के इस आर्टिकल में उत्पादन,आहार,परिवहन सम्बन्धी समस्याओं के इष्टतम हल ज्ञात करने के लिए कुछ सवालों को हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Top Tips of Vogel Approximation Method
2.कक्षा 12 में रैखिक प्रोग्रामन के साधित उदाहरण (Linear Programming in Class 12 Solved Illustrations):
Illustration:1.रेशमा दो प्रकार के भोज्य P और Q को इस प्रकार मिलाना चाहती है कि मिश्रण में विटामिन अवयवों में कम से कम 8 मात्रक विटामिन A तथा 11 मात्रक विटामिन B हों।भोज्य P की लागत Rs. 60/kg और भोज्य Q की लागत Rs. 80/kg है।भोज्य P में 3 मात्रक/kg विटामिन A और 5 मात्रक/kg विटामिन B है जबकि भोज्य Q में 4 मात्रक/kg विटामिन A और 2 मात्रक/kg विटामिन विटामिन B है।मिश्रण की न्यूनतम लागत ज्ञात कीजिए।
Solution:माना भोज्य P का x kg और भोज्य Q का y kg है।स्पष्टतः x \geq 0 ; y \geq 0
हम प्रदत्त आँकड़ों से निम्न सारणी बनाते हैंः
\begin{array}{|c|c|c|c|} \hline \text{ स्रोत } & \text{ भोज्य } & \text{ आवश्यकता} & \text{ (मात्रकों } \\ & \text{ पदार्थ } & & \text{ में )}\\ & P_x & Q_y & \\ \hline \text{विटामिन A } & 3 & 4 & 8 \\ \text{(मात्रक/kg) } & & & \\ \hline \text{विटामिन B} & 5 & 2 & 11\\ \text{ (मात्रक/kg)} & & & \\ \hline \text{लागत} & 60 & 80 & \\ \text{ (Rs/kg)} & & & \\ \hline \end{array}
दोनों भोज्यों की लागत=60x++80y
विटामिन A की कुल मात्रा 3x+4y कम से कम 8 होनी चाहिए अतः
3 x+4 y \geq 8
विटामिन B की कुल मात्रा 5 x+2 y कम से कम 11 होनी चाहिए अतः
5 x+2 y \geq 11
अतः समस्या का गणितीय सूत्रीकरण निम्नलिखित है:
उद्देश्य फलन Min Z=60x++80y
s.t. 3 x+4 y \geq 8 \\ 5x+2 y \geq 11 \\ x, y \geq 0
प्रतिबन्ध असमिकाओं के संगत समीकरण
3x+4y=8,5x+2y=11,x=0,y=0
3x+4y=8 में y=0 रखने पर : x=\frac{8}{3}
अब x=0 रखने पर y=2
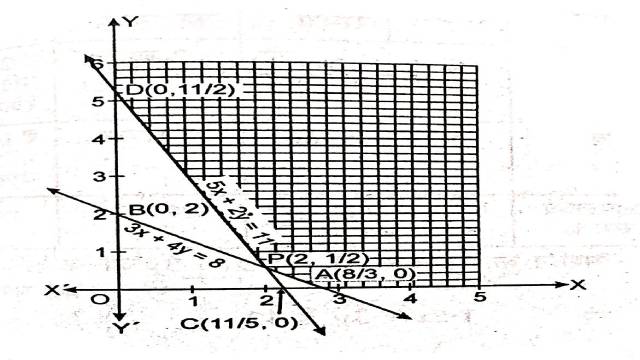
अतः यह अक्षों को A\left(\frac{8}{3},0 \right) और B(0,2) पर काटती है।
इसी प्रकार 5x+2y=11 में y=0 रखने पर x=\frac{11}{5}
अब x=0 रखने पर y=\frac{11}{2}
अतः यह अक्षों को C\left(\frac{11}{5}, 0\right) व D\left(0, \frac{11}{2}\right) पर काटती है।
3x+4y=8 व 6x+2y=11 का प्रतिच्छेद बिन्दु P\left(2, \frac{1}{2}\right) है।
3x+4y \geq 8 में x=0,y=0 रखने पर 3(0)+4(0) \geq 8 जो कि सत्य नहीं है।
5x+2 y \geq 11 में x=0,y=0 रखने पर 5(0)+2(0) \geq 11 जो कि सत्य नहीं है।अतः दोनों का हल क्षेत्र मूलबिन्दु से विपरीत ओर स्थित है।
x \geq 0 का क्षेत्र y-अक्ष पर और y-अक्ष के दायीं ओर है।
y \geq 0 का क्षेत्र x-अक्ष और x-अक्ष के ऊपर है।
इनसे बना उभयनिष्ठ छायांकित क्षेत्र YDPAX है।बहुभुज YDPAX के शीर्षों के निर्देशांक हैं:
D\left(0, \frac{11}{2}\right), P\left(2, \frac{1}{2}\right), A\left(\frac{8}{3}, 0\right)
उपर्युक्त शीर्षों पर उद्देश्य फलन (Z) के मानों की गणना निम्न प्रकार हैः
\begin{array}{|l|l|l|} \hline \text { शीष } & \text { निर्देशोक } & \text { उद्देश्य फलन Z का मान} \\ \hline D & \left(0, \frac{11}{2}\right) & 60 \times 0+80 \times \frac{11}{2}=440 \\ \hline P & \left(2, \frac{1}{2}\right) & 60 \times 2+80 \times \frac{1}{2}=160 \\ \hline A & \left(\frac{8}{3}, 0\right) & 60 \times \frac{8}{3}+80 \times 0=160 \\ \hline \end{array}
उपर्युक्त तालिका से स्पष्ट है कि उद्देश्य फलन Z का न्यूनतम मान 160 परन्तु सुसंगत क्षेत्र अपरिबद्ध है।असमिका 60x+80y<160 अर्थात् 3x+4y<8 के क्षेत्र और सुसंगत क्षेत्र में कोई भी उभयनिष्ठ नहीं है।अतः Z का न्यूनतम मान 160 है जो AD के प्रत्येक बिन्दु पर है।
Illustration:2.एक प्रकार के केक को 200g आटा तथा 50g वसा (fat) की आवश्यकता होती है तथा दूसरी प्रकार के केक के लिए 100g आटा तथा 50g वसा की आवश्यकता होती है।केकों की अधिकतम संख्या बताओ जो 5 किलो आटे तथा 1 किलो वसा से बन सकते हैं,यह मान लिया गया है कि केकों को बनाने के लिए अन्य पदार्थों की कमी नहीं रहेगी।
Solution:माना एक प्रकार की x केक और दूसरी प्रकार की y केक है।स्पष्टतः x \geq 0 ; y \geq 0
हम प्रदत्त आँकड़ों से निम्न सारणी बनाते हैंः
\begin{array}{|c|c|c|c|} \hline & \text { केक } & & \text { कुल } \\ & I & II \\ & x & y & x+y \\ \hline \text { आटा } & 200 \mathrm{~g} & 100 \mathrm{~g} & 5000 \mathrm{~g} \\ \hline \text { वसा } & 25 \mathrm{~g} & 50 \mathrm{~g} & 1000 \mathrm{~g} \\ \hline \end{array}
स्रोत भोज्य पदार्थ आवश्यकता (मात्रकों में)
दोनों भोज्यों की लागत=60x+80y
दोनों प्रकार के कुल केकों की संख्या=x+y
आटे की आवश्यकता 200x+100y अधिक से अधिक 5000 gm होनी चाहिए अतः
200 x+100 y \leq 5000 \\ \Rightarrow 2 x+y \leq 50
वसा की आवश्यकता 25x+50y अधिक से अधिक 1000 gm होनी चाहिए अतः
25 x+50 y \leq 1000 \\ \Rightarrow x+2 y \leq 40
अतः समस्या का गणितीय सूत्रीकरण निम्नलिखित है:
उद्देश्य फलन Max. Z=x+y
s.t. 2x+y \leq 50 \\ x+2 y \leq 40 \\ x, y \geq 0
प्रतिबन्ध असमिकाओं के संगत समीकरण
2x+y=50,x+2y=40,x=0,y=0
2x+y=60 में y=0 रखने पर x=25
अब x=0 रखने पर y=50
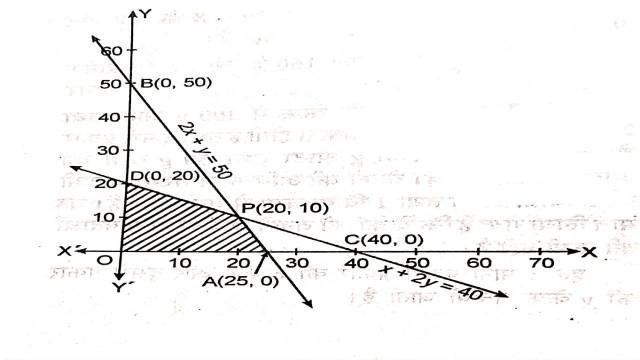
अतः यह अक्षों को A(25,0) और B(0,50) पर काटती है।
इसी प्रकार x+2y=40 में y=0 रखने पर x=40
अब x=0 रखने पर y=20
अतः यह अक्षों को C(40,0) व D(0,20) पर काटती है।
2x+y=50 व x+2y=40 का प्रतिच्छेद बिन्दु P(20,10) है।
2x+y \leq 50 में x=0,y=0 रखने पर 2(0)+0 \leq 50 \Rightarrow 0 \leq 50 जो कि सत्य है।
x+2 y \leq 40 में x=0,y=0 रखने पर 0+2(0) \leq 40 \Rightarrow 0 \leq 40 जो कि सत्य है।अतः दोनों का हल क्षेत्र मूलबिन्दु की ओर स्थित है।
x \geq 0 का क्षेत्र y-अक्ष पर और y-अक्ष के दायीं ओर है।
y \geq 0 का क्षेत्र x-अक्ष और x-अक्ष के ऊपर है।
इनसे बना उभयनिष्ठ क्षेत्र OAPD है।बहुभुज OAPD के शीर्षों के निर्देशांक हैं:
O(0,0),A(25,0),P(20,10),D(0,20)
उपर्युक्त शीर्षों पर उद्देश्य फलन (Z) के मानों की गणना निम्न प्रकार हैः
\begin{array}{|l|l|l|} \hline \text { शीर्ष } & \text { निर्देशांक } & \text { उद्देश्य फलन Z का मान } \\ \hline P & (0,0) & 0+0=0 \\ \hline A & (25,0) & 25+0=25 \\ \hline P & (20,10) & 20+10=30 \\ \hline P & (0,20) & 0+20=20 \\ \hline \end{array}
उपर्युक्त तालिका से स्पष्ट है कि उद्देश्य फलन Z का अधिकतम मान 30 जो बिन्दु P(20,10) पर है।
अतः x=20,y=10,Max Z=30
Illustration:3.एक कारखाने में टेनिस के रैकेट तथा क्रिकेट के बल्ले बनते हैं।एक टेनिस रैकेट बनाने के लिए 1.5 घण्टा यांत्रिक समय तथा 3 घण्टे शिल्पकार का समय लगता है।एक क्रिकेट बल्ले को तैयार करने में 3 घण्टे यान्त्रिक समय तथा 1 घण्टा शिल्पकार का समय लगता है।एक दिन में कारखाने में विभिन्न यन्त्रों पर उपलब्ध यान्त्रिक समय के 24 घण्टे से अधिक नहीं है।
(i)रैकेटों और बल्लों को कितनी संख्या में बनाया जाए ताकि कारखाना पूरी क्षमता से कार्य करे?
(ii)यदि रैकेट और बल्ले पर लाभ क्रमशः Rs. 20 तथा Rs. 10 हों तो कारखाने का अधिकतम लाभ ज्ञात कीजिए यदि कारखाना पूरी क्षमता से कार्य करे।
Solution:माना एक एक दिन में x रैकेट और y क्रिकेट के बल्ले बनाता है।स्पष्टतः x \geq 0 ; y \geq 0
हम प्रदत्त आँकड़ों से निम्न सारणी बनाते हैंः
\begin{array}{|l|l|l|l|} \hline \text{ आइटम } & \text{रैकेट} & \text{बल्ले} & \text{ उपलब्ध} \\ \hline \text{संख्या} & x & y & \text{समय} \\ \hline \text{मशीनी} & 1.5 \text{घण्टे} & 3 \text{घण्टे} & 42 \text{घण्टे} \\ \text{समय} & & & \\ \hline \text{शिल्पकार} & \text{3 घण्टे} & \text{ 1 घण्टा} & 24 \text{घण्टे} \\ \text{का समय} & & & \\ \hline \text{लाभ} & 20 \text{ प्रति } & 10 \text{ प्रति } & \\ & \text{ रैकेट } & \text{ बल्ले } & \\ \hline \end{array}
x और y रैकेटों व बल्लों पर लाभ=20x+10y
मशीन का कुल समय 1.5x+3y घण्टे जो अधिकतम 42 घण्टे हैं अतः
15x+3 y \leq 42 \\ x+2 y \leq 28
शिल्पकार का कुल समय 3x+y घण्टे जो अधिकतम 24 घण्टे हैं अतः
3 x+y \leq 24
अतः समस्या का गणितीय सूत्रीकरण निम्नलिखित है:
उद्देश्य फलन Max Z=20x+10y
s.t. x+2 y \leq 28 \\ 3 x+y \leq 24 \\ x, y \geq 0
प्रतिबन्ध असमिकाओं के संगत समीकरण
x+2y=28,3x+y=24,x=0,y=0
x+2y=28 में y=0 रखने पर x=28
अब x=0 रखने पर y=14
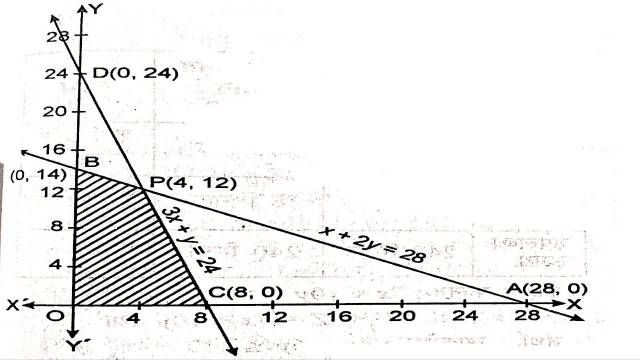
अतः यह अक्षों को A(24,0) और B(0,14) पर काटती है।
इसी प्रकार 3x+y=24 में y=0 रखने पर x=8
अब x=0 रखने पर y=24
अतः यह अक्षों को C(8,0) व D(0,24) पर काटती है।
x+2y=28 व 3x+y=24 का प्रतिच्छेद बिन्दु P(4,12) है।
x+2 y \leq 28 में x=0,y=0 रखने पर 0+2(0) \leq 28 \Rightarrow 0 \leq 28 जो कि सत्य है।
3x+y \leq 24 में x=0,y=0 रखने पर 3(0)+0 \leq 24 \Rightarrow 0 \leq 24 जो कि सत्य है।अतः दोनों का हल क्षेत्र मूलबिन्दु की ओर स्थित है।
x \geq 0 का क्षेत्र y-अक्ष पर और y-अक्ष के दायीं ओर है।
y \geq 0 का क्षेत्र x-अक्ष और x-अक्ष के ऊपर है।
इनसे बना उभयनिष्ठ क्षेत्र OCPB है।बहुभुज OCPB के शीर्षों के निर्देशांक हैं:
O(0,0),C(8,0),P(4,12),B(0,14)
उपर्युक्त शीर्षों पर उद्देश्य फलन (Z) के मानों की गणना निम्न प्रकार हैः
\begin{array}{|l|l|l|} \hline \text { शीर्ष } & \text { निर्देशांक } & \text { उद्देश्य फलन Z का मान } \\ \hline O & (0,0) & 20(0)+10(0)=0 \\ \hline C & (8,0) & 20 \times 8+10 \times 0=160 \\ \hline P & (4,12) & 20 \times 4+10 \times 12=200 \\ \hline A & (0,14) & 20 \times 0+14 \times 12=168 \\ \hline \end{array}
उपर्युक्त तालिका से स्पष्ट है कि उद्देश्य फलन Z का अधिकतम मान 200 रुपये है जो जब रैकेट 4 और 12 बल्ले बनाएँ जाते हैं।
Illustration:4.एक निर्माणकर्ता नट और बोल्ट का निर्माण करता है।एक पैकेट नटों के निर्माण में मशीन A पर एक घण्टा और मशीन B पर 3 घण्टे काम करना पड़ता है,जबकि एक पैकेट बोल्ट के निर्माण में 3 घण्टे मशीन A पर और 1 घण्टा मशीन B पर काम करना पड़ता है।वह नटों से Rs. 17.50 प्रति पैकेट और बोल्टों पर Rs. 7.00 प्रति पैकेट लाभ कमाता है।यदि प्रतिदिन मशीनों का अधिकतम उपयोग 12 घण्टे किया जाए तो प्रत्येक (नट और बोल्ट) के कितने पैकेट उत्पादित किए जाएँ ताकि अधिकतम लाभ कमाया जा सके।
Solution:माना x पैकेट नट और बोल्ट y पैकेट का उत्पादन किया जाता है।स्पष्टतः x \geq 0 ; y \geq 0
हम प्रदत्त आँकड़ों से निम्न सारणी बनाते हैंः
\begin{array}{|c|c|c|c|} \hline \text{आइटम} & \text{नट} & \text{बोल्ट} & \text{कुल} \\ & \text{ पैकेट} & \text{पैकेट} & \text{समय} \\ \hline \text{संख्या} & x & y & \\ \hline \text{मशीन A} & 1 & 3 & 12 \\ \text{ पर समय } & \text{ घण्टा} & \text{ घण्टे} & \text{ घण्टे} \\ \hline \text{मशीन B} & 3 & 1 & 12 \\ \text{ पर समय} & \text{ घण्टे} & \text{ घण्टा} & \text{ घण्टे} \\ \hline \text{लाभ} & \begin{array}{c} \text{17.50 प्रति } \\ \text{ पैकेट} \end{array} & \begin{array}{c} \text{ 7 प्रति } \\ \text{ पैकेट} \end{array} & \\ \hline \end{array}
x नट पैकेट और y बोल्ट पैकेट पर लाभ Max. Z=17.50x+7y
मशीन A का कुल उपयोग का समय x+3y घण्टे जो अधिकतम 12 घण्टे हैं अतः
x+3 y \leq 12
मशीन B का कुल उपयोग का समय 3x+y घण्टे जो अधिकतम 12 घण्टे हैं अतः
3 x+y \leq 12
अतः समस्या का गणितीय सूत्रीकरण निम्नलिखित है:
उद्देश्य फलन Max Z=17.60x+7y
s.t. x+3 y \leq 12 \\ 3x+y \leq 12 \\ x, y \geq 0
प्रतिबन्ध असमिकाओं के संगत समीकरण
x+3y=12,3x+y=12,x=0,y=0
x+3y=12 में y=0 रखने पर x=12
अब x=0 रखने पर y=4
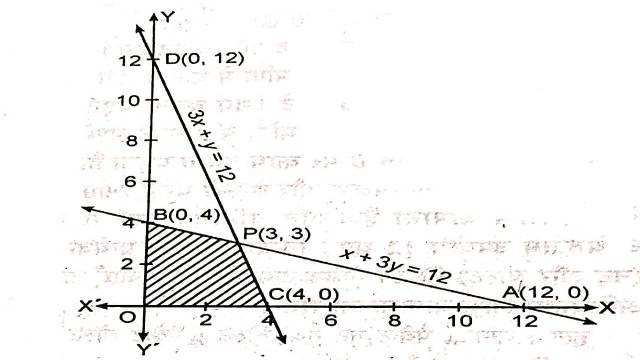
अतः यह अक्षों को A(12,0) और B(0,4) पर काटती है।
इसी प्रकार 3x+y=12 में y=0 रखने पर x=4
अब x=0 रखने पर y=12
अतः यह अक्षों को C(4,0) व D(0,12) पर काटती है।
x+3y=12 व 3x+y=12 का प्रतिच्छेद बिन्दु P(3,3) है।
x+3 y \leq 12 में x=0,y=0 रखने पर 0+3(0) \leq 12 \Rightarrow 0 \leq 12 जो कि सत्य है।
3 x+y \leq 12 में x=0,y=0 रखने पर 3(0)+0 \leq 12 \Rightarrow 0 \leq 12 जो कि सत्य है।अतः दोनों का हल क्षेत्र मूलबिन्दु की ओर स्थित है।
x \geq 0 का क्षेत्र y-अक्ष पर और y-अक्ष के दायीं ओर है।
y \geq 0 का क्षेत्र x-अक्ष और x-अक्ष के ऊपर है।
इनसे बना उभयनिष्ठ क्षेत्र OCPB है।बहुभुज OCPB के शीर्षों के निर्देशांक हैं:
O(0,0),C(4,0),P(3,3),B(0,4)
उपर्युक्त शीर्षों पर उद्देश्य फलन (Z) के मानों की गणना निम्न प्रकार हैः
\begin{array}{|l|l|l|} \hline \text { शीर्ष } & \text { निर्देशांक } & \text { उद्देश्य फलन Z का मान } \\ \hline O & (0,0) & 17.50 \times 0+7 \times 0=0 \\ \hline C & (4,0) & 17.50 \times 4+7 \times 0=70 \\ \hline P & (3,3) & 17.58 \times 3+7 \times 3=73.50 \\ \hline B & (0,4) & 17.50 \times 0+7 \times 4=28 \\ \hline \end{array}
उपर्युक्त तालिका से स्पष्ट है कि उद्देश्य फलन Z का अधिकतम मान 73.50 रुपये है जब नट पैकेट 3 और बोल्ट पैकेट 3 का उत्पादन किया जाए।
Illustration:5.एक कारखाने में दो प्रकार के पेंच A और B बनते हैं।प्रत्येक के निर्माण में दो मशीनों के प्रयोग की आवश्यकता होती है,जिसमें एक स्वचालित और दूसरी हस्तचालित है।एक पैकेट पेंच A के निर्माण में 4 मिनट स्वचालित और 6 मिनट हस्तचालित मशीन,तथा एक पैच B के निर्माण में,6 मिनट स्वचालित और 3 मिनट हस्तचालित मशीन का कार्य होता है।प्रत्येक मशीन किसी भी दिन के लिए अधिकतम 4 घण्टे काम के लिए उपलब्ध है।निर्माता A पेंच के प्रत्येक पैकेट पर Rs. 7 और पेंच B के प्रत्येक पेकेट पर Rs. 10 का लाभ कमाता है।यह मानते हुए कि कारखाने में निर्मित सभी पेंचों के पैकेट बिक जाते हैं,ज्ञात कीजिए कि प्रतिदिन कितने पैकेट विभिन्न पेंचों के बनाएं जाएं जिससे लाभ अधिकतम हो तथा अधिकतम लाभ ज्ञात कीजिए।
Solution:माना कारखाने में A प्रकार के x पैकेट पेंच और B प्रकार के y पैकेट पेंच प्रतिदिन बनाएँ जाते हैं।स्पष्टतः x \geq 0 ; y \geq 0
हम प्रदत्त आँकड़ों से निम्न सारणी बनाते हैंः
\begin{array}{|c|c|c|c|} \hline \text{पेंच के} & A & B & \text{ उपलब्ध } \\ \text{प्रकार} & & & \\ \hline & x & y & \text{ समय} \\ \hline \text{स्वचालित } & & & \\ \text{मशीन } & 4 & 6 & 240 \\ \text{पर समय } & \text{ मिनट } & \text{ मिनट } & \text{ मिनट } \\ \hline \text{हस्तचालित } & & & \\ \text{ मशीन} & 6 & 3 & 240 \\ \text{पर समय} & \text{ मिनट } & \text{ मिनट } & \text{ मिनट } \\ \hline \text{लाभ} & \text{7 Rs. } & \text{ 10 Rs. } & \\ & \text{प्रति पैकेट} & \text{प्रति पैकेट} & \\ \hline \end{array}
स्वचालित मशीन पर कुल 4x+6y जो अधिकतम 240 मिनट है अतः
4 x+6 y \leq 240 \Rightarrow 2 x+3 y \leq 120
हस्तचालित मशीन पर कुल समय 6x+3y जो अधिकतम 240 मिनट अतः
6 x+3 y \leq 240 \Rightarrow 2 x+y \leq 80
अतः समस्या का गणितीय सूत्रीकरण निम्नलिखित है:
उद्देश्य फलन Max Z=17.60x+7y
s.t. 2x+3 y \leq 120,2 x+y \leq 80, x, y \geq 0
प्रतिबन्ध असमिकाओं के संगत समीकरण
2x+3y=120,2x+y=80,x=0,y=0
2x+3y=120 में y=0 रखने पर x=60
अब x=0 रखने पर y=40
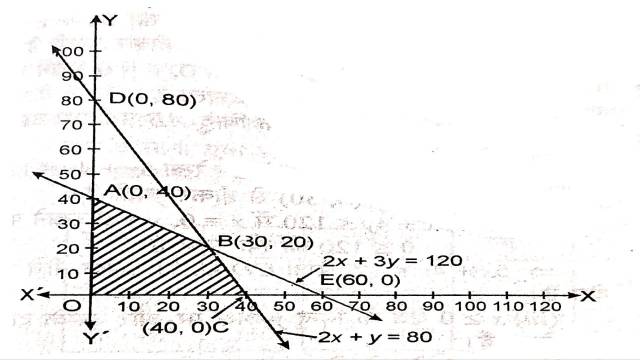
अतः यह अक्षों को E(60,0) और A(0,40) पर काटती है।
इसी प्रकार 2x+y=80 में y=0 रखने पर x=40
अब x=0 रखने पर y=80
अतः यह अक्षों को C(4,00) व D(0,80) पर काटती है।
2x+3y=120 व 2x+y=80 का प्रतिच्छेद बिन्दु B(30,20) है।
2 x+3 y \leq 120 में x=0,y=0 रखने पर 2(0)+3(0) \leq 120 \Rightarrow 0 \leq 120 जो कि सत्य है।
2x+y \leq 80 में x=0,y=0 रखने पर 2(0)+0 \leq 80 \Rightarrow 0 \leq 80 जो कि सत्य है।अतः दोनों का हल क्षेत्र मूलबिन्दु की ओर स्थित है।
x \geq 0 का क्षेत्र y-अक्ष पर और y-अक्ष के दायीं ओर है।
y \geq 0 का क्षेत्र x-अक्ष और x-अक्ष के ऊपर है।
इनसे बना उभयनिष्ठ क्षेत्र OABC है।बहुभुज OABC के शीर्षों के निर्देशांक हैं:
O(0,0),A(0,40),B(30,20),C(40,0)
उपर्युक्त शीर्षों पर उद्देश्य फलन (Z) के मानों की गणना निम्न प्रकार हैः
\begin{array}{|c|c|c|} \hline \text { शीर्ष } & \text { निर्देशांक } & \text { उद्देश्य फलन Z का मान } \\ \hline O & (0,0) & 7 \times 0+10 \times 0=0 \\ \hline A & (0,40) & 7 \times 0+10 \times 40=400 \\ \hline B & (30,20) & 7 \times 30+10 \times 20=410 \\ \hline C & (40,0) & 7 \times 40+10 \times 0=280 \\ \hline \end{array}
उपर्युक्त तालिका से स्पष्ट है कि उद्देश्य फलन Z का अधिकतम मान 410 है जब A प्रकार के पेचों के पैकेट 30 और B प्रकार के पेचों के पैकेट 20 का उत्पादन होता है।
Illustration:6.एक कुटीर उद्योग निर्माता पैडेस्टल लैंप और लकड़ी के शेड बनाता है।प्रत्येक के निर्माण में एक रगड़ने/काटने और एक स्प्रेयर की आवश्यकता पड़ती है।एक लैंप के निर्माण में 2 घण्टे रगड़ने/काटने और 3 घण्टे स्प्रेयर की आवश्यकता होती है,जबकि एक शेड के निर्माण में 1 घण्टा रगड़ने/काटने और 2 घण्टे स्प्रेयर की आवश्यकता होती है।स्प्रेयर की मशीन प्रतिदिन अधिकतम 20 घण्टे और रगड़ने/काटने की मशीन अधिकतम 12 घण्टे के लिए उपलब्ध है।एक लैंप की बिक्री पर रुपये 5 और एक शैड की बिक्री पर Rs. 3 का लाभ होता है।यह मानते हुए कि सभी निर्मित लैम्प और शेड बिक जाते हैं,तो बताइए वह निर्माण की प्रतिदिन कैसी योजना बनाएँ कि लाभ अधिकतम हो?
Solution:माना x लैम्प और y शेड प्रतिदिन उत्पादित किए जाते हैं।स्पष्टतः x \geq 0 ; y \geq 0
हम प्रदत्त आँकड़ों से निम्न सारणी बनाते हैंः
\begin{array}{|c|c|c|c|} \hline \text{आइटम} & \text{लैम्प} & \text{ शेड } & \text{ उपलब्ध } \\ \hline \text{संख्या} & x & y & \text{समय }\\ \hline \text{रगड़ने/} & & & \\ \text{काटने} & & & \\ \text{ की मशीन} & 2 & 1 & 12 \\ \text{ का समय } & \text{ घण्टे} & \text{ घण्टा} & \text{ घण्टे} \\ \hline \text{ स्पेयर} & & & \\ \text{मशीन} & 3 & 2 & 20 \\ \text{का समय } & \text{ घण्टे} & \text{ घण्टे} & \text{ घण्टे} \\ \hline \text{लाभ} & \text{5 घण्टे रु.} & \text{ 3 घण्टे रु. } & \\ & \text{ प्रति पैकेट } & \text{प्रति पैकेट } & \\ \hline \end{array}
रगड़ने काटने की मशीन पर कुल समय 2x+y जो अधिकतम 12 घण्टे है अतः
2 x+y \leq 12
स्पेयर मशीन पर कुल समय 3x+2y जो कि अधिकतम 20 घण्टे है अतः
3 x+2 y \leq 20
अतः समस्या का गणितीय सूत्रीकरण निम्नलिखित है:
उद्देश्य फलन Max Z=5x+3y
s.t. 2x+y \leq 12 \\ 3 x+2 y \leq 20 \\ x, y \geq 0
प्रतिबन्ध असमिकाओं के संगत समीकरण
2x+y=12,3x+2y=20,x=0,y=0
2x+y=120 में y=0 रखने पर x=6
अब x=0 रखने पर y=12
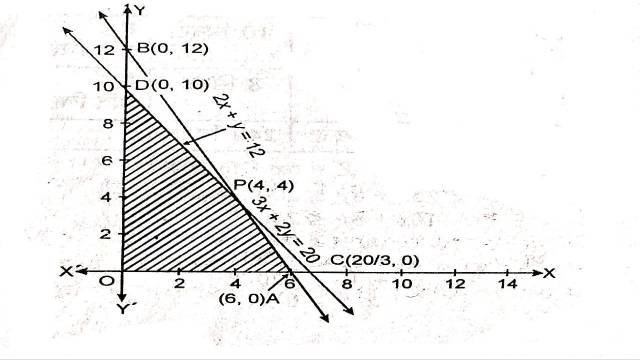
अतः यह अक्षों को A(6,0) और B(0,12) पर काटती है।
इसी प्रकार 3x+2y=20 में y=0 रखने पर x=\frac{20}{3}
अब x=0 रखने पर y=10
अतः यह अक्षों को C\left(\frac{20}{3}, 0\right) व D(0,10) पर काटती है।
2x+y=12 व 3x+2y=20 का प्रतिच्छेद बिन्दु P(4,4) है।
2 x+y \leq 12 में x=0,y=0 रखने पर 2(0)+0 \leq 12 \Rightarrow 0 \leq 12 जो कि सत्य है।
3x+2y \leq 20 में x=0,y=0 रखने पर 3(0)+2(0) \leq 20 \Rightarrow 0 \leq 20 जो कि सत्य है।अतः दोनों का हल क्षेत्र मूलबिन्दु की ओर स्थित है।
x \geq 0 का क्षेत्र y-अक्ष पर और y-अक्ष के दायीं ओर है।
y \geq 0 का क्षेत्र x-अक्ष और x-अक्ष के ऊपर है।
इनसे बना उभयनिष्ठ क्षेत्र OAPD है।बहुभुज OAPD के शीर्षों के निर्देशांक हैं:
O(0,0),A(6,0),P(4,4),D(0,10)
उपर्युक्त शीर्षों पर उद्देश्य फलन (Z) के मानों की गणना निम्न प्रकार हैः
\begin{array}{|l|l|l|} \hline \text { शीर्ष } & \text { निर्देशांक } & \text { उद्देश्य फलन Z का मान } \\ \hline O & (0,0) & 5 \times 0+3 \times 0=0 \\ A & (6,0) & 5 \times 6+3 \times 0=30 \\ P & (4,4) & 5 \times 4+3 \times 4=32 \\ D & (0,10) & 5 \times 0+3 \times 10=30 \\ \hline \end{array}
उपर्युक्त तालिका से स्पष्ट है कि उद्देश्य फलन Z का अधिकतम मान 32 है जब 4 लैम्प और 4 शैड का उत्पादन किया जाता है।
उपर्युक्त उदाहरणों के द्वारा कक्षा 12 में रैखिक प्रोग्रामन (Linear Programming in Class 12),रैखिक प्रोग्रामन (Linear Programming) को समझ सकते हैं।
3.कक्षा 12 में रैखिक प्रोग्रामन पर आधारित सवाल (Questions Based on Linear Programming in Class 12):
(1.)एक फर्म c_1, c_2, c_3 तीन प्रकार के कपड़े बनाती हैं।इन कपड़ों के लिए लाल,हरी और नीली तीन प्रकार की ऊन की आवश्यकता पड़ती है। c_1 कपड़े की एक इकाई लम्बाई के लिए 2 मी. लाल और 3 मी. नीली ऊन, c_2 कपड़े की एक इकाई लम्बाई के लिए 3 मी. लाल 2 मी. हरी और 2 मी. नीली ऊन तथा c_3 कपड़े की एक इकाई के लिए 5 मीटर हरी और 4 मी. नीली ऊन की आवश्यकता पड़ती है।फर्म के पास 16 मी. लाल ऊन,20 मी. हरी ऊन और 30 मी. नीली ऊन का स्टाॅक है। c_1, c_2, c_3 के लिए प्रति इकाई लम्बाई अनुमानित लाभ क्रमशः 6 रु.,10 रु. और 8 रु. हो तो बताइए कि फर्म को अपना स्टाॅक किस प्रकार प्रयोग में लेना चाहिए ताकि उसे अधिकतम लाभ हो। (समस्या का गणितीय संरूपण कीजिए)।
(2.)एक कम्पनी A और B नमूने की दो चमड़े की बेल्ट बनाती है।बेल्ट A उच्च प्रकार की एवं बेल्ट B घटिया प्रकार की है।दोनों बेल्टों पर लाभ क्रमशः 40 और 30 पैसे प्रति बेल्ट है।A प्रकार के एक बेल्ट के बनाने में B प्रकार की एक बेल्ट बनाने से दुगुना समय लगता है।यदि सब बेल्ट B नमूने की हो,तो कम्पनी 1000 बेल्ट प्रतिदिन बना सकती है,परन्तु चमड़े की पूर्ति 800 (A और B दोनों को मिलाकर) बेल्ट प्रतिदिन के लिए पर्याप्त है।बेल्ट A के लिए एक फैन्सी बकल चाहिए और उसके लिए केवल 400 बकल प्रतिदिन उपलब्ध हैं।बेल्ट B के लिए केवल 700 बकल प्रतिदिन प्राप्त है।अधिकतम लाभ के लिए कम्पनी दोनों तरह की बेल्ट कितनी बनाए,लेखाचित्र विधि से हल करते हुए इष्टतम हल ज्ञात कीजिए।
उत्तर (Answers):(1.) Max. Z=6 x_1+10 x_2+8 x_3 \\ \text { s.t. } 2 x_1+3 x_2 \leq 16 \\ 2 x_2+5 x_3 \leq 20 \\ 3 x_1+2 x_2+4 x_3 \leq 30 तथा x_1, x_2, x_3 \geq 0
(2.) x_1=200, x_2=600 तथा Max Z=260 रुपए
उपर्युक्त सवालों को हल करने पर कक्षा 12 में रैखिक प्रोग्रामन (Linear Programming in Class 12),रैखिक प्रोग्रामन (Frequently Asked Questions Related to Linear Programming) को ठीक से समझ सकते हैं।
Also Read This Article:- Tips of Vogel Approximation Method
4.कक्षा 12 में रैखिक प्रोग्रामन (Linear Programming in Class 12),रैखिक प्रोग्रामन (Linear Programming) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.सुसंगत क्षेत्र का पता कैसे लगाएँ? (How to Find Feasible Region?):
उत्तर:सुसंगत क्षेत्र प्रदत्त समस्या के लिए एक रैखिक प्रोग्रामन समस्या के ऋणेतर व्यवरोध x,y \geq 0 सहित सभी व्यवरोधों द्वारा नियत उभयनिष्ठ क्षेत्र सुसंगत क्षेत्र (या हल क्षेत्र) कहलाता है।
प्रश्न:2.सुसंगत हल समूह से क्या आशय है? (What Do You Mean by Feasible Solution?):
उत्तर:सुसंगत हल समूह सुसंगत क्षेत्र के अंतः भाग तथा सीमा के सभी बिन्दु व्यवरोधों के सुसंगत हल कहलाते हैं।
प्रश्न:3.इष्टतम/अनुकूलतम हल क्या होता है? (What is the Optimal Solution?):
उत्तर:इष्टतम/अनुकूलतम (सुसंगत) हल:सुसंगत क्षेत्र में कोई बिन्दु जो उद्देश्य फलन का इष्टतम मान (अधिकतम या न्यूनतम) दें,एक इष्टतम हल कहलाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा कक्षा 12 में रैखिक प्रोग्रामन (Linear Programming in Class 12),रैखिक प्रोग्रामन (Linear Programming) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here | |
| 7. | click here |
Linear Programming in Class 12
कक्षा 12 में रैखिक प्रोग्रामन
(Linear Programming in Class 12)
Linear Programming in Class 12
कक्षा 12 में रैखिक प्रोग्रामन (Linear Programming in Class 12) के इस आर्टिकल में
उत्पादन,आहार,परिवहन सम्बन्धी समस्याओं के इष्टतम हल ज्ञात करने के लिए कुछ सवालों
को हल करके समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.