Areas of Combinations of Plane Figures
1.समतल आकृतियों के संयोजनों के क्षेत्रफल (Areas of Combinations of Plane Figures),समतल आकृतियों के संयोजनों के क्षेत्रफल कक्षा 10 (Areas of Combinations of Plane Figures Class 10):
समतल आकृतियों के संयोजनों के क्षेत्रफल (Areas of Combinations of Plane Figures) ज्ञात करने का प्रयत्न करेंगे।हमें इस प्रकार की आकृतियाँ दैनिक जीवन में तथा विभिन्न रोचक डिजाइनों के रूप में देखने को मिलती हैं।फूलों की क्यारियाँ,नालियों के ढक्कन,खिड़कियों के डिजाइन,मेज पोशों पर बने डिजाइन आदि ऐसी आकृतियों के कुछ उदाहरण हैं।इन आकृतियों के क्षेत्रफल ज्ञात करने की प्रक्रिया को हम कुछ उदाहरणों द्वारा स्पष्ट करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Areas Related to Circles Class 10
2.समतल आकृतियों के संयोजनों के क्षेत्रफल के साधित उदाहरण (Areas of Combinations of Plane Figures Solved Examples):
(जब तक अन्यथा न कहा जाए, \pi=\frac{22}{7} का प्रयोग कीजिए।)
Example:1.आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए,यदि PQ=24 cm,PR=7 cm तथा Q वृत्त का केन्द्र है।
Solution: \angle QPR=90^{\circ} (अर्धवृत्त में बना कोण समकोण होता है)
समकोण \triangle PQR में
RQ^2=PQ^2+PR^2 (पाइथागोरस प्रमेय से)
=(24)^2+(7)^2 \\=576+49 \\=625 \\ \Rightarrow RQ=\sqrt{625}=25 cm
अर्धवृत्त का क्षेत्रफल=\frac{1}{2} \pi r^2 \\ =\frac{1}{2} \times \frac{22}{7} \times \frac{25}{2} \times \frac{25}{2}=\frac{6875}{28}
समकोण \triangle PQR का क्षेत्रफल=
=\frac{1}{2} \times \text { आधार } \times \text { ऊँचाई } \\ =\frac{1}{2} \times P Q \times P R \\ =\frac{1}{2} \times 24 \times 7 \\ =84 \mathrm{~cm}^2
छायांकित भाग का क्षेत्रफल=\frac{6875}{28}-84 \\ =\frac{6875-2352}{28} \\ =\frac{4523}{28} \mathrm{~cm}^2
Example:2.आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए यदि केन्द्र O वाले दोनों संकेन्द्रीय वृत्तों की त्रिज्याएँ क्रमशः 7 cm और 14 cm हैं तथा \angle AOC=40^{\circ} है।
Solution:छोटे वृत्त में बने त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360}=\frac{22}{7} \times \frac{7 \times 7 \times 40}{360} \\ =\frac{154}{9} \mathrm{~cm}^2
बड़े वृत्त में बने त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi R^2 \theta}{360} \\ =\frac{22}{7} \times \frac{14 \times 14 \times 40}{360}=\frac{616}{9}
छायांकित भाग का क्षेत्रफल=\frac{616}{9}-\frac{154}{9} \\ =\frac{616-154}{9}=\frac{462}{9} \\ =\frac{154}{3} \mathrm{~cm}^2
Example:3.आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए,यदि ABCD भुजा 14 cm का एक वर्ग है तथा APD और BPC दो अर्धवृत्त हैं।
Solution:अर्धवृत्त की त्रिज्या r=\frac{14}{2}=7 सेमी
दोनों समान अर्धवृत्तों का क्षेत्रफल=वृत्त का क्षेत्रफल
= \pi r^2 \\ = \frac{22}{7} \times 7 \times 7=154 \mathrm{~cm}^2
वर्ग का क्षेत्रफल=\text{ भुजा }^{2}=14 \times 14 =196 वर्गसेमी
छायांकित भाग का क्षेत्रफल=196-154
=42 वर्गसेमी
Example:4.आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए,जहाँ भुजा 12 cm वाले एक समबाहु त्रिभुज OAB के शीर्ष O को केन्द्र मान कर 6 सेमी त्रिज्या वाला एक वृत्तीय चाप खींचा गया है।
Solution:वृत्त की त्रिज्या r=6 cm
वृत्त का क्षेत्रफल=\pi r^2 \\ =\frac{22}{7} \times 6 \times 6=\frac{792}{7} \mathrm{~cm}^2
समबाहु त्रिभुज का क्षेत्रफल=\frac{\sqrt{3}}{4} \text { भुजा }^{2} \\ =\frac{\sqrt{3}}{4} \times 12 \times 12=36 \sqrt{3}
त्रिज्यखण्ड का केन्द्र पर बना कोण=\theta=60^{\circ}
त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360} \\ =\frac{22}{7} \times \frac{ 6 \times 6 \times 60}{360} \\ =\frac{132}{7} \mathrm{~cm}^2
छायांकित भाग का क्षेत्रफल=\frac{792}{7}+36 \sqrt{3}-\frac{132}{7} \\ =\left(\frac{660}{7}+36 \sqrt{3}\right) \mathrm{~cm}^2
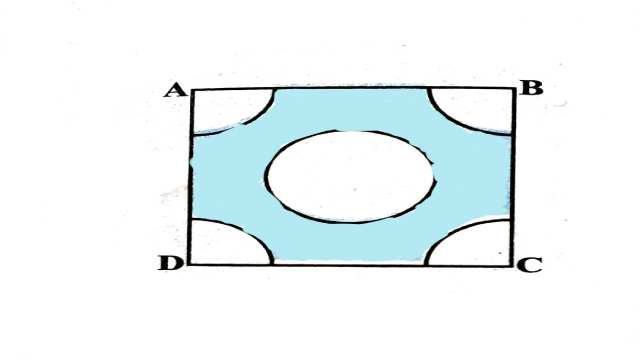
Example:5.भुजा 4 cm वाले एक वर्ग के प्रत्येक कोने से 1 cm त्रिज्या वाले वृत्त का एक चतुर्थांश काटा गया है तथा बीच में 2 cm व्यास का एक वृत्त भी काटा गया है जैसाकि आकृति में दर्शाया गया है।वर्ग के शेष भाग का क्षेत्रफल ज्ञात कीजिए।
Solution:वर्ग ABCD का क्षेत्रफल=\text { भुजा }^{2} \\=4^2=16 \mathrm{~cm}^2
बीच में बने वृत्त का क्षेत्रफल =\pi r^2 \\ =\frac{22}{7} \times 1 \times 1=\frac{22}{7} \mathrm{~cm}^2
एक समान त्रिज्यखण्डों का क्षेत्रफल=वृत्त का क्षेत्रफल
=\pi r^2 \\ =\frac{22}{7} \times 1 \times 1=\frac{22}{7} \mathrm{~cm}^2
वर्ग के शेष भाग का क्षेत्रफल=16-\frac{22}{7}-\frac{22}{7} \\ =\frac{112-44}{7}=\frac{68 }{7}\mathrm{~cm}^2
Example:6.एक वृत्ताकार मेजपोश,जिसकी त्रिज्या 32 cm है, में बीच में एक समबाहु त्रिभुज ABC छोड़ते हुए एक डिजाइन बना हुआ है,जैसा कि आकृति में दिखाया गया है।इस डिजाइन का क्षेत्रफल ज्ञात कीजिए।
Solution:वृत्ताकार मेजपोश के बीच में समबाहु त्रिभुज बना हुआ है।
अतः तीन समान वृत्तखण्डों द्वारा केन्द्र पर अन्तरित कोण=360°
एक वृत्तखण्ड द्वारा केन्द्र पर अन्तरित कोण=\theta=\frac{360^{\circ}}{3}=120^{\circ}
अतः छायांकित भाग का क्षेत्रफल=3 वृत्तखण्डों का क्षेत्रफल
=3\left(\frac{\pi r^2 \theta}{360}-r^2 \sin \frac{\theta}{2} \cos \frac{\theta}{2}\right) \\ =3\left(\frac{22}{7} \times \frac{32 \times 32 \times 120}{360}-32 \times 32 \times \sin 60 \cos 60\right) \\ =3\left(\frac{22528}{21}-256 \sqrt{3}\right) \\ =\left(\frac{22528}{7}-768 \sqrt{3}\right) \mathrm{cm}^2
Example:7.आकृति में,ABCD भुजा 14 cm वाला वर्ग है।A,B,C और D को केन्द्र मानकर चार वृत्त इस प्रकार खींचे गए हैं कि प्रत्येक वृत्त शेष तीन वृत्तों में से दो वृत्तों को बाह्य रूप से स्पर्श करता है।छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
Solution:वृत्त की त्रिज्या=\frac{14}{2}=7 सेमी
चार समान त्रिज्यखण्डों का क्षेत्रफल=वृत्त का क्षेत्रफल
=\pi r^2=\frac{22}{7} \times 7 \times 7=154
वर्ग ABCD का क्षेत्रफल=\text{ भुजा }^{2} =14^2=196
छायांकित भाग का क्षेत्रफल=196-154=42 वर्गसेमी
Example:8.आकृति एक दौड़ने का पथ (racing track) दर्शाती है,जिसके बाएँ और दाएँ सिरे अर्धवृत्ताकार है।
दोनों आन्तरिक समान्तर रेखाखण्डों के बीच की दूरी 60 m है तथा इनमें से प्रत्येक रेखाखण्ड 106 m लम्बा है।यदि यह पथ 10 m चौड़ा है,तो ज्ञात कीजिए।
(i)पथ के आन्तरिक किनारों के अनुदिश एक पूरा चक्कर लगाने में चली गई दूरी
(ii)पथ का क्षेत्रफल
Solution:(i)आन्तरिक अर्धवृत्तों की त्रिज्या=\frac{60}{2}
r=30 m
आन्तरिक दोनों समान अर्धवृत्तों की परिधि=2 \pi r \\ =2 \times \frac{22}{7} \times 30=\frac{1320}{7} m
आन्तरिक आयताकार भाग के दोनों सिरों की लम्बाई=106×2=212 m
पथ के आन्तरिक किनारों के अनुदिश एक चक्कर में चली गई दूरी=212+\frac{1320}{7} \\ =\frac{1484+1320}{7} \\ =\frac{2804}{7} m
(ii)आन्तरिक दोनों अर्धवृत्तों का क्षेत्रफल=\pi r^2 \\ =\frac{22}{7} \times 30 \times 30=\frac{19800}{7} \mathrm{~m}^2
बाह्य अर्धवृत्त की त्रिज्या=30+10=40 मीटर
बाह्य दोनों अर्धवृत्तों का क्षेत्रफल=\pi R^{2} \\ =\frac{22}{7} \times 40 \times 40=\frac{35200}{7}
आन्तरिक आयताकार भाग का क्षेत्रफल=106×60=6360 वर्गमीटर
बाह्य आयताकार भाग की चौड़ाई=60+10+10
=80 मीटर
बाह्य आयताकार भाग का क्षेत्रफल=लम्बाई × चौड़ाई
=106×80
=8480 वर्गमीटर
पथ का क्षेत्रफल=8480+\frac{35200}{7}-6360-\frac{19800}{7} \\ =2120+\frac{15400}{7} \\ =2120+2200 \\ =4320 \mathrm{~m}^2
Example:9.आकृति में,AB और CD केन्द्र O वाले एक वृत्त के दो परस्पर लम्ब व्यास हैं तथा OD छोटे वृत्त का व्यास है।यदि OA=7 cm है तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
Solution:छोटे वृत्त का व्यास=OD=OA=7 cm
छोटे वृत्त की त्रिज्या (r)=\frac{7}{2} cm
छोटे वृत्त का क्षेत्रफल=\pi r^{2} \\=\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}=38.5 \mathrm{~cm}^2
बड़े वृत्त की त्रिज्या=7 cm
वृत्तखण्ड का केन्द्र पर अन्तरित कोण \theta=90°
दोनों समान वृत्तखण्डों का क्षेत्रफल=2\left(\frac{\pi r^2 \theta}{360}-\frac{r^2}{2} \sin \theta\right) \\ =2\left(\frac{22}{7} \times \frac{7 \times 7 \times 90}{360}-\frac{7 \times 7}{2} \sin 90\right) \\ =2(38.5-24.5) \\ =2 \times 14 \\ =28 \mathrm{~cm}^2
छायांकित भाग का क्षेत्रफल=38.5+28
=66.5 वर्गसेमी
Example:10.एक समबाहु त्रिभुज ABC का क्षेत्रफल 17320.5 वर्गसेमी है।इस त्रिभुज की भुजा के आधे के बराबर त्रिज्या लेकर एक वृत्त खींचा जाता है (देखिए आकृति)।छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (\pi=3.14 और \sqrt{3}=1.73205 लीजिए।)
Solution:तीन समान त्रिज्यखण्डों का क्षेत्रफल=3 \times \frac{ \pi r^2 \theta}{360}=\frac{3 \pi r^2 \times 60}{360}=\frac{\pi r^2}{2}
छायांकित भाग का क्षेत्रफल=त्रिभुज का क्षेत्रफल-तीन समान त्रिज्यखण्डों का क्षेत्रफल
समबाहु त्रिभुज का क्षेत्रफल=\frac{\sqrt{3}}{4} \text{ भुजा }^{2} \\ \Rightarrow \frac{1.73203}{4} \times x^2=173205 \mathrm{~cm}^2 \\ \Rightarrow x^2=\frac{173205 \times 4}{1,73205} \times \frac{100000}{10} \\ \Rightarrow x^2=40000 \Rightarrow x=200 \mathrm{~cm}
वृत्त की त्रिज्या(r)=\frac{x}{2}=100 cm
छायांकित भाग का क्षेत्रफल=17320.5-\frac{\pi r^2}{2} \\ =17320.5-\frac{\pi \times 100 \times 100}{2} \\ =17320.5-3.14 \times 100 \times 50 \\ =17320.5-15700 \\ =1620.5 \mathrm{~cm}^2
Example:11.एक वर्गाकार रूमाल पर,नौ वृत्ताकार डिजाइन बने हैं,जिनमें प्रत्येक की त्रिज्या 7 cm है (देखिए आकृति)।रूमाल के शेष भाग का क्षेत्रफल ज्ञात कीजिए।
Solution:वृत्त की त्रिज्या (r)=7 cm
नौ वृत्तों का क्षेत्रफल=9 \pi r^2 \\ =9 \times \frac{22}{7} \times 7 \times 7=1386 \mathrm{~cm}^2
वर्ग की भुजा=6×वृत्त की त्रिज्या
=6×7=42 सेमी
वर्ग का क्षेत्रफल=\text {भुजा }^{2}=42×42=1764 वर्गसेमी
रूमाल के शेषभाग का क्षेत्रफल=1764-1386
=378 वर्गसेमी
Example:12.आकृति में,OACB केन्द्र O और त्रिज्या 3.5 cm वाले एक वृत्त का चतुर्थांश है।यदि OD=2 cm है,तो निम्नलिखित के क्षेत्रफल ज्ञात कीजिए।
Example:12(i).चतुर्थांश OACB
Solution:वृत्त के चतुर्थांश का क्षेत्रफल=\frac{1}{4} \times \frac{22}{7} \times 3.5 \times 3.5 \\ =9.625 \mathrm{~cm}^2 \\ =\frac{9625}{1000} \\ =\frac{77}{8} \mathrm{~cm}^2
Example:12(ii).छायांकित भाग का क्षेत्रफल
Solution:समकोण \triangle BOD का क्षेत्रफल
=\frac{1}{2} \times \text { आधार } \times \text { ऊँचाई } \\ =\frac{1}{2} \times BO \times OD \\ =\frac{1}{2} \times 3.5 \times 2 \\ =35 \mathrm{~cm}^2=\frac{7}{2} \mathrm{~cm}^2
छायांकित भाग का क्षेत्रफल=\frac{77}{8}-\frac{7}{2} \\ =\frac{77-28}{8}=\frac{49}{8} \mathrm{~cm}^2
Example:13.आकृति में, एक चतुर्थांश OPBQ के अन्तर्गत एक वर्ग OACB बना हुआ है।यदि OA=20 cm है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए (\pi=3.14 लीजिए।)।
Solution:वृत्त की त्रिज्या=
OB^2=OA^2+AB^2 \\ \Rightarrow OB^2 =20^2+20^2 \\ =400+400 \\ =800 \\ \Rightarrow OB=\sqrt{800} \\ OB =20 \sqrt{2}
वृत्त के चतुर्थांश (\theta=90°) का क्षेत्रफल=\frac{\pi r^2 \theta}{360} \\ =\frac{3.14 \times 20 \sqrt{2} \times 20 \sqrt{2} \times 90}{360} \\ =628
वर्ग का क्षेत्रफल=\text {भुजा}^{2}=20 \times 20=400
छायांकित भाग का क्षेत्रफल=628-400=228 वर्गसेमी
Example:14.AB और CD केन्द्र O तथा त्रिज्याओं 21 cm और 7 cm वाले दो संकेन्द्रीय वृत्तों के क्रमशः दो चाप हैं (देखिए आकृति)।यदि \angle AOB=30° है,तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
Solution:21 सेमी त्रिज्या वाले त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360} \\ r=21, \theta=30^{\circ} \\ =\frac{22}{7} \times \frac{21 \times 21 \times 30}{360} \\ =\frac{231}{2} \mathrm{~cm}^2
7 सेमी त्रिज्या वाले त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi R^2 \theta}{360} \\ R=7, \theta =30 \\ =\frac{22}{7} \times \frac{7 \times 7 \times 30}{360}=\frac{77}{6} \mathrm{~cm}^2
छायांकित भाग का क्षेत्रफल=\frac{231}{2}-\frac{77}{6} \\ =\frac{693-77}{6}=\frac{616}{6} \\ =\frac{308}{3} \mathrm{~cm}^2
Example:15.आकृति में,ABC त्रिज्या 14 cm वाले एक वृत्त का चतुर्थांश है तथा BC को व्यास मानकर एक अर्धवृत्त खींचा गया है।छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
Solution:समकोण \triangle AOB में
BC^2=A C^2+A B^2 \\ =14^2+14^2 \\ =196+196 \\ =392 \\ BC =\sqrt{392} \\ 2R =14 \sqrt{2} \mathrm{~cm}
वृत्त के चतुर्थांश का क्षेत्रफल =\frac{\pi r^2 \theta}{360} \\ \theta=90^{\circ}, r=14 cm \\ =\frac{22}{7} \times \frac{14 \times 14 \times 90}{360} \\ =154 \mathrm{~cm}^2
वृत्तखण्ड का क्षेत्रफल=154-\frac{r^2}{2} \sin \theta \\ =154-\frac{14 \times 14}{2} \sin 90 \\ =154-98 \\ =56 \mathrm{~cm}^2
अर्धवृत्त का क्षेत्रफल=\frac{1}{2} \pi R^2 \\ =\frac{1}{2} \times \frac{22}{7} \times \frac{14 \sqrt{2}}{2} \times \frac{14 \sqrt{2}}{2} \\ =154\mathrm{~cm}^2
छायांकित भाग का क्षेत्रफल=154-56
=98 वर्गसेमी
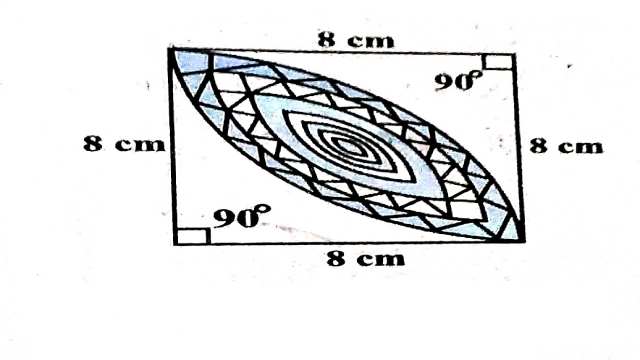
Example:16.आकृति में, छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए, जो 8 cm त्रिज्याओं वाले दो वृत्तों के चतुर्थांशों के बीच उभयनिष्ठ है।
Solution:दो समान वृत्तखण्डों का क्षेत्रफल=2\left(\frac{\pi r^2 \theta}{560}-\frac{r^2}{2} \sin \theta\right) \\ =2\left(\frac{22}{7} \times \frac{8 \times 8 \times 90}{360}-\frac{8 \times 8}{2} \sin 90\right) \\ =2\left(\frac{352}{7}-32 \times 1\right) \\ =2\left(\frac{352-224}{7}\right) \\ =2\left(\frac{128}{7}\right) \\ =\frac{256}{7} \mathrm{~cm}^2
उपर्युक्त उदाहरणों के द्वारा समतल आकृतियों के संयोजनों के क्षेत्रफल (Areas of Combinations of Plane Figures),समतल आकृतियों के संयोजनों के क्षेत्रफल कक्षा 10 (Areas of Combinations of Plane Figures Class 10) को समझ सकते हैं।
3.समतल आकृतियों के संयोजनों के क्षेत्रफल के सवाल (Areas of Combinations of Plane Figures Questions):
(1.)दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (\pi=\frac{22}{7} लीजिए)
(2.)आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (\pi=\frac{22}{7} लीजिए)
उपर्युक्त सवालों को हल करने पर समतल आकृतियों के संयोजनों के क्षेत्रफल (Areas of Combinations of Plane Figures),समतल आकृतियों के संयोजनों के क्षेत्रफल कक्षा 10 (Areas of Combinations of Plane Figures Class 10) को ठीक से समझ सकते हैं।
Also Read This Article:-Areas of Sector and Segment of Circle
4.समतल आकृतियों के संयोजनों के क्षेत्रफल (Frequently Asked Questions Related to Areas of Combinations of Plane Figures),समतल आकृतियों के संयोजनों के क्षेत्रफल कक्षा 10 (Areas of Combinations of Plane Figures Class 10) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.वृत्त के त्रिज्यखण्ड का परिमाप कैसे ज्ञात करते हैं? (How Do You Find the Perimeter of the Sector?):
उत्तर:निम्नलिखित सूत्र से वृत्त के त्रिज्यखण्ड का परिमाप ज्ञात करते हैंः
=2 r+l=2 r+\frac{\pi r \theta}{180}
प्रश्न:2.वृत्तखण्ड का परिमाप कैसे ज्ञात करते हैं? (How to Find the Perimeter of a Segment?):
उत्तर:निम्नलिखित सूत्र के द्वारा वृत्तखण्ड का परिमाप ज्ञात करते हैंः
=2 \sin \frac{\theta}{2}+\frac{\pi r \theta}{180^{\circ}}
प्रश्न:3.त्रिज्यखण्ड और वृत्तखण्ड की महत्त्वपूर्ण बातें लिखिए। (Write Down the Important Points of Sector and Segment of a Circle):
उत्तर:(1.)त्रिज्या r वाले वृत्त की परिधि=2 \pi r
(2.)त्रिज्या r वाले वृत्त का क्षेत्रफल=\pi r^{2}
(3.)त्रिज्या r वाले वृत्त के एक त्रिज्यखण्ड जिसका कोण अंशों \theta में है,के संगत चाप की लम्बाई=\frac{\theta}{360} \times 2 \pi r=\frac{\pi r \theta}{180^{\circ}}
(4.)त्रिज्या r वाले वृत्त के एक त्रिज्यखण्ड,जिसका कोण अंशों में है,का क्षेत्रफल=\frac{\pi r^2 \theta}{360^{\circ}}
(5.)एक वृत्तखण्ड का क्षेत्रफल=संगत त्रिज्यखण्ड का क्षेत्रफल-संगत त्रिभुज का क्षेत्रफल
=\frac{\pi r^2 \theta}{360^{\circ}}-\frac{r^2}{2} \sin \theta
यदि \theta का मान 90° से अधिक हो तो
=\frac{\pi r^2 \theta}{360^{\circ}}-r^2 \sin \frac{\theta}{2} \cos \frac{\theta}{2}
उपर्युक्त प्रश्नों के उत्तर द्वारा समतल आकृतियों के संयोजनों के क्षेत्रफल (Areas of Combinations of Plane Figures),समतल आकृतियों के संयोजनों के क्षेत्रफल कक्षा 10 (Areas of Combinations of Plane Figures Class 10) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Areas of Combinations of Plane Figures
समतल आकृतियों के संयोजनों के क्षेत्रफल
(Areas of Combinations of Plane Figures)
Areas of Combinations of Plane Figures
समतल आकृतियों के संयोजनों के क्षेत्रफल (Areas of Combinations of Plane Figures) ज्ञात
करने का प्रयत्न करेंगे।हमें इस प्रकार की आकृतियाँ दैनिक जीवन में तथा विभिन्न रोचक डिजाइनों के
रूप में देखने को मिलती हैं।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.