Singular Solution in DE
1.डिफरेंशियल इक्वेशन में विचित्र हल (Singular Solution in DE),अवकल समीकरण में विचित्र हल (Singular Solution in Differential Equations):
डिफरेंशियल इक्वेशन में विचित्र हल (Singular Solution in DE) किसी अवकल समीकरण का वह हल जो उसके व्यापक हल में स्वेच्छ अचर को विशिष्ट मान देने पर प्राप्त नहीं होता,उसको अवकल समीकरण का विचित्र हल (singular solution) कहते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Equations Reducible to Clairaut’s Form
2.डिफरेंशियल इक्वेशन में विचित्र हल के उदाहरण (Singular Solution in DE Examples);
निम्नलिखित अवकल समीकरणों के व्यापक हल,विचित्र हल तथा बाह्य बिन्दु-पथ ज्ञात कीजिए:
(Find the general solution,singular solution and extraneous loci of the following differential equations):
Example:1. y=x p+p^2
Solution: y=x p+p^2 \cdots(1)
अब इसका x के सापेक्ष अवकलन करने पर:
\frac{d y}{d x}=p+x \frac{d p}{d x}+2 p \frac{d p}{d x} \\ \Rightarrow p=p+x \frac{d p}{d x}+2 p \frac{d p}{d x} \\ \Rightarrow \frac{d p}{d x}(x+2 p)=0 \cdots(2) \\ \Rightarrow \frac{d p}{d x}=0 तथा x+2p=0 \\ \frac{d p}{d x}=0 का समाकलन करने पर:
p=c…..(3)
(1) और (3) से p का विलोपन करने पर:
y=c x+c^2 \cdots(4)
जो कि दिए हुए समीकरण का व्यापक हल है।
c-विवेचक: c^2+c x-y=0 \\ B^2-4 A C=0 \\ \Rightarrow x^2+4 y=0
p-विवेचक: x^2+4 y=0 [(1) से]
निष्कर्ष:यहाँ x^2+4 y=0 केवल एक बार दोनों विविक्तिकरों में आया है,अतः यह हल दिए हुए समीकरण का विचित्र हल है तथा अन्वालोप है।
व्यापक हल: y=c x+c^2
विचित्र हल: x^2+4 y=0
Example:8. 4 y p^2+2 p x-y=0
Solution: 4 y p^2+2 p x-y=0
दिए हुए समीकरण को निम्न प्रकार लिखा जा सकता है:
2 p x=y-4 y p^2 \\ \Rightarrow x=\frac{y}{2 p}-2 y p \cdots(1)
अब इसका y के सापेक्ष अवकलन करने पर:
व्यापक हल ज्ञात करने के लिए (\frac{1}{2 p}+2 p) को छोड़ देते हैं क्योंकि इससे विचित्र हल प्राप्त होता है।
अतः 1+\frac{y}{b} \frac{d r}{d y}=0 \\ \Rightarrow \frac{d p}{p}=-\frac{d y}{y}
इसका समाकलन करने पर हमें प्राप्त होगा:
\log p=-\log y+\log c \\ \Rightarrow p=\frac{c}{2} \cdots(3)
अब (1) और (3) से p का विलोपन करने पर:
x=\frac{y}{2} \times \frac{y}{c}-2 y \times \frac{c}{y} \\ \Rightarrow x=\frac{y^2}{2 c}-2 c \\ \Rightarrow y^2=2 c x+4 c^2
जो कि दिए हुए समीकरण का व्यापक हल है।
c-विवेचक: 4 c^2+2 c x-y^2=0 \\ B^2-4 A C=0 \\ \Rightarrow (2 x)^2-4 \times 4 \left(-y^2\right)=0 \\ \Rightarrow 4 x^2+16 y^2=0 \\ \Rightarrow x^2+4 y^2=0
p-विवेचक: 4 y b^2+2 p x-y=0 \\ B^2-4 A C=0 \\ \Rightarrow(2 x)^2-4 \times 4 y-(-y)=0 \\ \Rightarrow 4 x^2+16 y^2=0 \\ \Rightarrow x^2+4 y^2=0 \\ x^2+4 y^2=0
निष्कर्ष:यहाँ केवल एक बार दोनों विविक्तिकरों में आया है,अतः यह हल दिए हुए समीकरण का विचित्र हल है।
व्यापक हल: y^2=2 c x+4 c^2
विचित्र हल: x^2+4 y^2=0
Example:9. x p^2-(x-a)^2=0
Solution: x p^2-(x-a)^2=0 \\ \Rightarrow x p^2=(x-a)^2 \\ \Rightarrow p^2=\frac{(x-a)^2}{x} \\ \Rightarrow p=\frac{x-a}{\sqrt{x}} \\ \Rightarrow \frac{d y}{d x}=\frac{x-a}{\sqrt{x}} \\ \Rightarrow \frac{d y}{d x}=\sqrt{x}-\frac{a}{\sqrt{x}} \\ \Rightarrow d y=\sqrt{x} d x-\frac{a}{\sqrt{x}} d x
दोनों पक्षों का समाकलन करने पर:
\Rightarrow \int d y=\int \sqrt{x} d x-\int \frac{a}{\sqrt{x}} d x\\ \Rightarrow y+c=\frac{2}{3} x^{\frac{3}{2}} -2 a \sqrt{x} \\ (y+c)=\frac{2 \sqrt{x}}{3}(x-3 a) \\ \Rightarrow 9(y+c)^2=4 x(x-3 a)^2
जो कि दिए हुए समीकरण का व्यापक हल है।
9(y+c)^2=4 x(x-3 a)^2 \\ \Rightarrow 9 c^2+18 c y+9 y^2-4 x(x-3 a)^2=0 \\ B^2-4 A C=0 \\ \Rightarrow (18 y)^2-4 \times 9 \times\left[9 y^2-4 x(x-3 a)^2\right]=0 \\ \Rightarrow 324 y^2-36\left[9 y^2-4 x(x-3 a)^2\right]=0 \\ \Rightarrow 36\left[9 y^2-9 y^2+4 x(x-3 a)^2\right]=0 \\ \Rightarrow 4 x(x-3 a)^2=0
c-विवेचक: x p^2-(x-a)^2=0 \\ B^2-4 AC=0 \\ \Rightarrow 0^2-4 \times x \times\left[-(x-a)^2\right] =0 \\ \Rightarrow 4 x(x-a)^2=0
p-विवेचक:
निष्कर्ष:यहाँ x=0 केवल एक बार दोनों विविक्तिकरों में आया है तथा दिए हुए समीकरण को सन्तुष्ट करता है,अतः यह हल दिए हुए समीकरण का विचित्र हल है।
x-3a=0,c-विवेचक में दो बार आया है,अतः यह नोड पथ है।
x-a=0,p-विवेचक में दो बार आया है,अतः यह स्पर्श बिन्दुपथ है।
व्यापक हल: 9(x+c)^2=4 x(x-3 a)^2 \\ x-3 a=0
विचित्र हल:x=0
नोड पथ: x-3a=0
स्पर्श बिन्दुपथ: x-a=0
Example:10. y^2-2 p x y+p^2\left(x^2-1\right)=m^2
Solution: y^2-2 p x y+p^2\left(x^2-1\right)=m^2 \\ \Rightarrow y^2-2 p x y+p^2\left(x^2-1\right) -m^2=0 \\ y =\frac{2 p x \pm \sqrt{(-2 p x)^2-4 \times 1\times\left[p^2\left(x^2-1\right)-m^2\right]}}{2 x 1} \\=\frac{2 p x \pm \sqrt{4 p^2 x^2-4 p^2 x^2+4 p^2+4 m^2}}{2} \\ =\frac{2 p x \pm 2 \sqrt{p^2+m^2}}{2} \\ \Rightarrow y =p x \pm \sqrt{p^2+m^2}
यह y के रूप में द्विघात समीकरण है,अतः
जो कि क्लैरो के रूप का समीकरण है।अतः इसका व्यापक हल होगा:
y=c x \pm \sqrt{c^2+m^2} \\ \Rightarrow(y-c x)^2=c^2+m^2
जो कि दिए हुए समीकरण का व्यापक हल है।
c-विवेचक: c^2\left(1-x^2\right)+2 c x y+m^2-y^2=0 \\ B^2-4 A C=0 \\ \Rightarrow(2 x y)^2-4 x\left(1-x^2\right)\left(m^2-y^2\right)=0 \\ \Rightarrow 4 x^2 y^2-4\left(m^2-y^2-x^2 m^2+x^2 y^2\right)=0 \\ \Rightarrow 4\left[^2 y^2-m^2+y^2+x^2 m^2-x^2 y^2\right]=0 \\ \Rightarrow x^2 m^2+y^2-m^2=0 \\ \Rightarrow y^2+m^2 x^2=m^2
p-विवेचक: p^2\left(x^2-1\right)-2 p x y+y^2-m^2=0 \\ B^2-4 A C=0 \\ \Rightarrow(-2 x y)^2-4\left(x^2-1\right)\left(y^2-m^2\right)=0 \ \Rightarrow 4 x^2 y^2-4\left[x^2 y^2-x^2 m^2-y^2+m^2 \right]=0 \\ \Rightarrow 4\left[x^2 y^2-x^2 y^2+x^2 m^2+y^2-m^2\right]=0 \\ \Rightarrow y^2+x^2 m^2=m^2
निष्कर्ष:यहाँ y^2+m^2 x^2=m^2 केवल एक बार दोनों विविक्तिकरों में आया है,अतः यह हल दिए हुए समीकरण का विचित्र हल है।
व्यापक हल: (y-c x)^2=c^2+m^2
विचित्र हल: y^2+x^2 m^2=m^2
Example:11. 9 p^2(2-y)^2=4(3-y)
Solution: 9 p^2(2-y)^2=4(3-y) \\ \Rightarrow p^2=\frac{4(3-y)}{9(2-y)^2} \\ \Rightarrow p=\frac{2 \sqrt{(3-y)}}{3(2-y)} \\ \Rightarrow \frac{d y}{d x}=\frac{2 \sqrt{(3-y)}}{3(2-y)} \\ \Rightarrow d x=\frac{3}{2} \frac{(2-y)}{\sqrt{(3-y)}} d y
दोनों पक्षों का समाकलन करने पर:
\int d x=\frac{3}{2} \int \frac{2-y}{\sqrt{(3-y)}} d y \\ \Rightarrow x=\frac{3}{2} \int \frac{3-y-1}{\sqrt{(3-y)}} d y \\=\frac{3}{2} \int \sqrt{3-y} d y-\frac{3}{2} \int \frac{1}{\sqrt{(3-y)}} d y \\ =\frac{3}{2} \times-\frac{2}{3}(3-y)^{\frac{3}{2}}+\frac{3}{2} \times 2(3-y)^{\frac{1}{2}}+c \\ \Rightarrow x-c=(3-y)^{\frac{1}{2}}(-3+y+3) \\ \Rightarrow(x-c)^2=y^2(3-y)
c-विवेचक: c^2-2cx+x^2-y^2(3-y)=0 \\ B^2-4 A C=0 \\ \Rightarrow(-2 x)^2-4 \times 1 x-\left[x^2-y^2(3-y)\right]=0 \\ \Rightarrow 4\left[x^2-x^2+y^2(3-y)\right]=0 \\ \Rightarrow y^2(3-y)=0 \\ \Rightarrow y^2(y-3)=0
p-विवेचक: 9 p^2(2-y)^2-4(3-y)=0 \\ B^2-4 A C=0 \\ \Rightarrow 0^2-4 \times 9(2-y)^2 \times-4(3-y)=0 \\ \Rightarrow (y-2)^2(y-3)=0
निष्कर्ष:यहाँ y-3=0 केवल एक बार दोनों विविक्तिकरों में आया है,अतः यह हल दिए हुए समीकरण का विचित्र हल है।
y-2=0,p-विवेचक में दो बार आया है अतः यह स्पर्श बिन्दुपथ है।
y=0,c-विवेचक में दो बार आया है अतः यह नोड बिन्दुपथ है।
व्यापक हल: (x-c)^2=y^2(3-y)
विचित्र हल:y-3=0
स्पर्श बिन्दुपथ:y-2=0
नोड बिन्दुपथ:y=0
Example:12. y^2\left(1+4 p^2\right)-2 p x y-1=0
Solution: y^2\left(1+4 p^2\right)-2 p x y-1=0 \cdots(1)
दिए हुए समीकरण को निम्न प्रकार लिखा जा सकता है:
2 p x y=y^2+4 y^2 p^2-1 \\ \Rightarrow x=\frac{y}{2 p}+2 y p-\frac{1}{2 p y}
अब दोनों पक्षों का y के सापेक्ष अवकलन करने पर:
\frac{d x}{d y}=\frac{1}{2 p}-\frac{y}{2p} \frac{dp}{dy} +2 p+2 y \frac{d p}{d y}+\frac{1}{2 p y^2}+ \frac{1}{2 y p^2} \frac{dp}{dy} \\ \Rightarrow \frac{1}{p}=\frac{1}{2 p}+2 p+\frac{1}{2 p y^2}+\frac{d p}{d y}\left(\frac{-y}{2 p^2}+2 y+\frac{1}{2 y p 2}\right) \\ \Rightarrow \left(-\frac{1}{p}+\frac{1}{2 p}+2 p+\frac{1}{2 p y^2} \right) +\frac{y}{p} \frac{d p}{d y}\left(-\frac{1}{2 p}+2 p+\frac{1}{2 y^2 p}\right)=0 \\ \Rightarrow \left(-\frac{1}{2 p}+2 p+\frac{1}{2 p y^2}\right)+\frac{y}{p} \frac{d p}{d y}\left(-\frac{1}{2 p}+2 p+\frac{1}{2 y^2 p}\right)=0 \\ \Rightarrow \left(1+\frac{y}{p} \frac{d p}{d y}\right)\left(-\frac{1}{2 p}+2 p+\frac{1}{2 p y^2}\right)=0
व्यापक हल ज्ञात करने के लिए हम गुणनखण्ड \left(-\frac{1}{2 p}+2 p+\frac{1}{2 p y^2}\right) को छोड़ देते हैं क्योंकि इससे विचित्र हल प्राप्त होता है।
1+\frac{y}{p} \frac{d p}{d y}=0 \\ \frac{d p}{p}=-\frac{d y}{y}
दोनों पक्षों का समाकलन करने पर:
\log p=-\log y+\log c \\ \Rightarrow p=\frac{c}{y}
p का मान समीकरण (1) में रखने पर:
y^2\left(1+\frac{4 c^2}{y^2}\right)-2 x y \times \frac{c}{y}-1=0 \\ \Rightarrow y^2+4 c^2-2 c x-1=0 \\ \Rightarrow y^2+4 c^2=1+2 c x
जो कि दिए हुए समीकरण का व्यापक हल है।
c-विवेचक: 4 c^2-2 c x+y^2-1=0 \\ B^2-4 A C=0 \\ (-2 x)^2-4 \times 4 \times\left(y^2-1\right)=0 \\ \Rightarrow x^2-4 y^2+4=0
p-विवेचक: 4 y^2 b^2-2 p x y+y^2-1=0 \\ B^2-4 A c=0 \\ (-2 x y)^2-4 \times 4 y^2 \times\left(y^2-1\right)=0 \\ \Rightarrow 4 x^2 y^2-16 y^4+16 y^2=0 \\ \Rightarrow 4 y^2\left(x^2-4 y^2+4\right)=0 \\ \Rightarrow y^2\left(x^2-4 y^2+4\right)=0
निष्कर्ष:यहाँ x^2-4 y^2+4=0 केवल एक बार दोनों विविक्तिकरों में आया है,अतः यह हल दिए हुए समीकरण का विचित्र हल है।
y=0,p-विवेचक में दो बार आया है अतः यह स्पर्श बिन्दुपथ है।
व्यापक हल: y^2+4 c^2=1+2 c x
विचित्र हल: x^2-4 y^2+4=0
स्पर्श बिन्दुपथ:y=0
Example:13. 4 x(x-1)(x-2) p^2-\left(3 x^2-6 x+2\right)^2=0
Solution: 4 x(x-1)(x-2) p^2-\left(3 x^2-6 x+2\right)^2=0 \\ \Rightarrow 4 p^2=\frac{\left(3 x^2-6 x+2\right)^2}{x(x-1)(x-2)} \\ \Rightarrow 4 p^2=\frac{\left(3 x^2-6 x+2\right)^2}{x(x-1)(x-2)} \\ \Rightarrow 2 p=\frac{3 x^2-6 x+2}{\sqrt{x^2-3 x^2+2 x}} \\ \Rightarrow 2 d y=\frac{3 x^2-6 x+2}{\sqrt{x^3-3 x^2+2 x}} \\ \Rightarrow 2 d y=\frac{3 x^2-6 x+2}{\sqrt{\left(x^3-3 x^2+2 x\right)}} d x
दोनों पक्षों का समाकलन करने पर:
2 \int d y=\int \frac{3 x^2-6 x+2}{\sqrt{\left(x^3-3 x^2+2 x\right)}} d x \\ y+c=\sqrt{\left(x^3-3 x^2+2 x\right)} \\ \Rightarrow(x+c)^2=x(x-1)(x-2)
जो कि दिए हुए समीकरण का व्यापक हल है।
c-विवेचक: y^2+2 c y+c^2-\left(x^3-3 x^2+2 x\right)=0 \\ B^2-4 A c=0 \\ \Rightarrow(2 y)^2-4 \times 1 \times\left[y^2-\left(x^3-3 x^2+2 x\right)\right]=0 \\ \Rightarrow 4 y^2-4 y^2+4 x(x-1)(x-2)=0 \\ \Rightarrow x(x-1)(x-2)=0
p-विवेचक: 4 x(x-1)(x-2) p^2-\left(3 x^2-6 x+2\right)^2 \\ B^2-4 A C=0 \\ \Rightarrow 0^2-4 \times x(x-1)(x-2)\left[-\left(3 x^2-6 x+2\right)^2\right]=0 \\ \Rightarrow x(x-1)(x-2)\left(3 x^2-6 x+2 \right)^2=0
निष्कर्ष:यहाँ x=0,x-1=0,x-2=0 केवल एक बार दोनों विविक्तिकरों में आया है,अतः यह हल दिए हुए समीकरण का विचित्र हल है।
3 x^2-6 x+2=0 \Rightarrow x=\frac{6 \pm \sqrt{(-6)^2-4 \times 3 \times 2}}{2 \times 3} \\ \Rightarrow x=\frac{6 \pm \sqrt{36-24}}{6} \\ \Rightarrow x=\frac{6 \pm \sqrt{12}}{6} \\ \Rightarrow x=\frac{6 \pm 2 \sqrt{3}}{6} \\ \Rightarrow x=1 \pm \frac{1}{\sqrt{3}}
p-विवेचक में दो बार आया है अतः यह स्पर्श बिन्दुपथ है।
व्यापक हल: (y+c)^2=x(x-1)(x-2)
विचित्र हल: x=0, x=1, x=2
स्पर्श बिन्दुपथ: x=1 \pm \frac{1}{\sqrt{3}}
Example:15. (p x-y)(x-p y)=2 p
Solution: (p x-y)(x-p y)=2 p \cdots(1)
दिए हुए समीकरण को क्लैरो के समीकरण में बदला जा सकता है,यदि हम निम्न प्रतिस्थापन करें:
x^2=4 तथा y^2=v
इसका x के सापेक्ष अवकलन करने पर:
2 x d x=d u, 2 y d y=d v \\ \frac{y}{x} \frac{d y}{d x}=\frac{d v}{d u}
माना \frac{d v}{d x}=P \\ \Rightarrow \sqrt{\frac{v}{u}} p=P \\ \Rightarrow p=\sqrt{\frac{u}{v}} P
p का समीकरण (1) में रखने पर:
\left(\sqrt{\frac{u}{v} P} \cdot \sqrt{u}-\sqrt{v}\right)\left(\sqrt{u}-\sqrt{\frac{u}{v}}P \sqrt{v}\right)=2 \sqrt{\frac{u}{v}} P\\ \Rightarrow \frac{(u P-v)}{\sqrt{v}} \cdot \sqrt{u}(1-P)=2 \sqrt{\frac{u}{v}} P \\ \Rightarrow u P-v=\frac{2 P}{1-p} \\ \Rightarrow v=u P+\frac{2 P}{P-1}
यह क्लैरो के रूप का समीकरण है,अतः इसका व्यापक हल होगा।
v=c u+\frac{2 c}{c-1} \\ \Rightarrow y^2=c x^2+\frac{2 c}{c-1} \\ \Rightarrow c y^2-y^2=c^2 x^2-c x^2+2 c \\ \Rightarrow c^2 x^2-c\left(x^2+y^2-2\right)+y^2=0
जो कि दिए हुए समीकरण का व्यापक हल है।
c-विवेचक: c^2 x^2-c\left(x^2+y^2-2\right)+y^2=0 \\ B^2-4 A C=0 \\ \Rightarrow\left[-\left(x^2 +y^2-2\right)\right]^2-4 x^2 \times y^2=0 \\ \Rightarrow\left(x^2+y^2-2\right)^2-4 x^2 y^2=0 \\ \Rightarrow x^4+y^4+4+2 x^2 y^2-4 y^2-4 x^2-4 x^2 y^2=0 \\ \Rightarrow x^4-2 x^2 y^2+y^4-4 x^2-4 y^2+4=0
p-विवेचक: p^2 u-p(u+v-2)+v=0 \\ B^2-4 A C=0 \\ \Rightarrow {[-(u+v-2)]^2-4 \times u v=0 } \\ \Rightarrow (u+v-2)^2-4 u v=0 \\ \Rightarrow u^2+v^2+4+2 u v-4 v-4 u-4 u v=0 \\ \Rightarrow u^2-2 u v+v^2-4 u-u v+u=0 \\ \Rightarrow x^4-2 x^2 y^2+y^4-4 x^2-4 y^2+4=0
निष्कर्ष:यहाँ x^4-2 x^2 y^2+y^4-4 x^2-4 y^2+4=0 केवल एक बार दोनों विविक्तिकरों में आया है,अतः यह हल दिए हुए समीकरण का विचित्र हल है।
व्यापक हल: c^2 x^2-c\left(x^2+y^2-2\right)+y^2=0
विचित्र हल: x^4-2 x^2 y^2+y^4-4 x^2-4 y^2+4=0
Example:16. x^2 p^2-3 p x y+2 y^2+x^3=0
Solution: x^2 p^2-3 p x y+2 y^2+x^3=0 \cdots(1)
दिए हुए समीकरण को क्लैरो के समीकरण में बदला जा सकता है,यदि हम निम्न प्रतिस्थापन करें:
x=u तथा \frac{y}{x}=v
इसका x के सापेक्ष अवकलन करने पर:
1=\frac{d u}{d x} , \frac{x \frac{d y}{d x}-y \cdot 1}{x^2}=\frac{d v}{d x} \\ \frac{d v}{d u}=\frac{x p-y}{x^2}
माना \frac{d v}{d u}=P \\ \Rightarrow P=\frac{p}{x}-\frac{y}{x^2} \\ \Rightarrow P=\frac{p}{u}-\frac{v}{u} \\ \Rightarrow P u+v=p
p का समीकरण (1) में रखने पर:
u^2(Pu+v)^2-3(Pu+v) u^2 \cdot v+2 u^2 v^2+u^3=0 \\ \Rightarrow (P u+v)^2-3(P u+v) \cdot v+2 v^2+u=0 \\ \Rightarrow P^2 u^2+2 Pu v+v^2-3 P u v-3 v^2+2 v^2+u=0 \\ \Rightarrow Pu v=P^2 u^2+u \\ \Rightarrow v=P u+\frac{1}{P}
यह क्लैरो के रूप का समीकरण है,अतः इसका व्यापक हल होगा।
v=c u+\frac{1}{c} \\ \Rightarrow \frac{y}{x}=c x+\frac{1}{c}\\ \Rightarrow y=c x^2+\frac{x}{c}
जो कि दिए हुए समीकरण का व्यापक हल है।
c-विवेचक: c^2 x^2-c y+x=0 \\ B^2-4 A C=0 \\ \Rightarrow(-y)^2-4 \times x^2 \times x=0 \\ \Rightarrow y^2-4 x^3=0
p-विवेचक: P^2 u-Pv+1=0 \\ B^2-4 A C=0 \\ \Rightarrow(-v)^2-4 \times u \times 1=0 \\ \Rightarrow v^2-4 u=0 \\ \Rightarrow \frac{y^2}{2 x^2}-4 x=0 \\ \Rightarrow y^2-4 x^3=0
निष्कर्ष:यहाँ y^2-4 x^3=0 केवल एक बार दोनों विविक्तिकरों में आया है,अतः यह हल दिए हुए समीकरण का विचित्र हल है।
व्यापक हल: y=c x^2+\frac{x}{c}
विचित्र हल: y^2-4 x^3=0
Example:17. x p^2-2 y p+x+2 y=0
Solution: x p^2-2 y p+x+2 y=0 \cdots(1)
दिए हुए समीकरण को क्लैरो के समीकरण में बदला जा सकता है,यदि हम निम्न प्रतिस्थापन करें:
x^2=u तथा y-x=v
इसका x के सापेक्ष अवकलन करने पर:
2 x=\frac{d u}{d x}, \frac{d y}{d x}-1=\frac{d v}{d x} \\ \Rightarrow \frac{d v}{d u}=\frac{\frac{d y}{d x}-1}{2x}
माना \frac{d v}{du}=P \\ \Rightarrow P=\frac{p-1}{2 \sqrt{u}} \\ \Rightarrow P=2 \sqrt{u} p+1
p का समीकरण (1) में रखने पर:
\sqrt{u}(2 \sqrt{u} P+1)^2-2 p(y-x)-2 p x+3 x+2(y-x)=0 \\ \Rightarrow \sqrt{u}(2 \sqrt{u} P+1)^2-2(2 \sqrt{u} P+1) v-2(2 \sqrt{u} P+1) \sqrt{u} + 3 \sqrt{u}+2 v=0 \\ \Rightarrow \sqrt{u}(2 \sqrt{u} P+1)^2-4 \sqrt{u} v p-2 v-4 u P-2 \sqrt{u} +3 \sqrt{u}+2 v=0 \\ \Rightarrow \sqrt{u}\left(4 u P^2+4 \sqrt{u} p+1 \right)-4 \sqrt{u} v P-4 u P +\sqrt{u}=0 \\ \Rightarrow 4 u p^2+4 \sqrt{u} P+1-4 v P-4 \sqrt{u} P+1=0 \\ \Rightarrow 4 v P=4 u P^2+1 \\ \Rightarrow v=u p+\frac{1}{4 P}
यह क्लैरो के रूप का समीकरण है,अतः इसका व्यापक हल होगा।
\Rightarrow v=c u+\frac{1}{4 c} \\ \Rightarrow y-x=c x^2+\frac{1}{4 c} \\ \Rightarrow 4 c^2 x^2-4 c(y-x)+1=0
जो कि दिए हुए समीकरण का व्यापक हल है।
c-विवेचक: 4 c^2 x^2-4 c(y-x)+1=0 \\ B^2-4 A C=0 \\ \Rightarrow[-4(y-x)]^2-4 \times 4 x^2 \times 1=0 \\ \Rightarrow 16(y-x)^2-16 x^2=0 \\ \Rightarrow (y-x)^2=x^2
p-विवेचक: 4 up^2-4 v p+1=0 \\ B^2-4 A C=0 \\ (-4 v)^2-4 \times 4 u \times 1=0 \\ \Rightarrow v^2-u=0 \\ \Rightarrow(y-x)^2=x^2
निष्कर्ष:यहाँ (y-x)^2=x^2 केवल एक बार दोनों विविक्तिकरों में आया है,अतः यह हल दिए हुए समीकरण का विचित्र हल है।
व्यापक हल: 4 c^2 x^2-4 c(y-x)+1=0
विचित्र हल: (y-x)^2=x^2
उपर्युक्त उदाहरणों के द्वारा डिफरेंशियल इक्वेशन में विचित्र हल (Singular Solution in DE),अवकल समीकरण में विचित्र हल (Singular Solution in Differential Equations) को समझ सकते हैं।
3.डिफरेंशियल इक्वेशन में विचित्र हल की समस्याएँ (Singular Solution in DE Problems):
निम्नलिखित अवकल समीकरणों के व्यापक हल,विचित्र हल तथा बाह्य बिन्दु-पथ ज्ञात कीजिए:
(Find the general solution,singular solution and extraneous loci of the following differential equations):
(1.) y=p x+p^3
(2.) p=\log (p x-y)
उत्तर (Answers):(1.)व्यापक हल: y=cx+c^3
विचित्र हल: 27 y^2+4 x^2=0
(2.)व्यापक हल: y=c x-c^2
विचित्र हल: y=x(\log x-1)
उपर्युक्त सवालों को हल करने पर डिफरेंशियल इक्वेशन में विचित्र हल (Singular Solution in DE),अवकल समीकरण में विचित्र हल (Singular Solution in Differential Equations) को ठीक से समझ सकते हैं।
Also Read This Article:- Lagrange Equation in DE
4.डिफरेंशियल इक्वेशन में विचित्र हल (Frequently Asked Questions Related to Singular Solution in DE),अवकल समीकरण में विचित्र हल (Singular Solution in Differential Equations) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.बाह्य बिन्दुपथ किसे कहते हैं? (What is Extraneous Locus?):
उत्तर:यदि \psi(x, y)=0 किसी दिए हुए अवकल समीकरण \phi(x, y, p)=0 का एक विचित्र हल (singular solution) है।तब यह c-विवेचक तथा p-विवेचक दोनों में निहित (contained) होता है।इन विवेचकों में अन्य गुणनखण्ड (factors) भी विद्यमान हो सकते हैं,जिनसे अन्वालोप के अलावा कोई ओर बिन्दुपथ (locus) भी प्राप्त किए जा सकते हैं।सामान्यतया ये बिन्दुपथ दिए हुए समीकरण को सन्तुष्ट नहीं करते,अतः ये बाह्य बिन्दुपथ (extraneous loci) कहलाते हैं।यहाँ हम स्पर्श बिन्दुपथ (Tac Locus),नोड-पथ (Node Locus) तथा उभयाग्र पथ (cusp locus) का विवेचन करेंगे,जो सभी बाह्य बिन्दुपथ हैं।
प्रश्न:2.स्पर्श बिन्दुपथ किसे कहते हैं? (What is Tac Locus?):
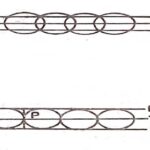
उत्तर:यदि p-विवेचक सम्बन्ध को सन्तुष्ट करने वाला कोई बिन्दु p हो,परिभाषानुसार बिन्दु P पर बिन्दु p के दो मान समान होंगे।p के ये दो समान मान वक्र-कुल के उन दो वक्रों के संगत होंगे,जो क्रमागत (consecutive) नहीं है,परन्तु जो एक-दूसरे को बिन्दु p पर स्पर्श करते हैं।अतः P एक वक्र-कुल के दो अक्रमागत (non-consecutive) वक्रों का स्पर्श-बिन्दु (point of contact) है तथा P का बिन्दुपथ वक्र कुल का स्पर्श बिन्दुपथ (Tac Locus) कहलाता है।अब यदि T(x,y)=0 स्पर्श बिन्दुपथ का समीकरण हो,तो यह p-विवेचक का एक गुणनखण्ड होगा परन्तु c-विवेचक का एक गुणनखण्ड नहीं होगा,क्योंकि स्पर्श करनेवाले वक्र अक्रमागत वक्र हैं,जिनमें c के मान असमान होंगे।
मानलो एक वृत्त-कुल दिया गया है जिसके वृत्तों के अर्द्धव्यास बराबर हैं जिसके वृत्तों के केन्द्र (centres) एक रैखिक है,परन्तु दो क्रमागत वक्र दो बिन्दुओं में कटते हैं।
स्पर्श की सीमान्त स्थिति में सभी स्पर्श-बिन्दु केन्द्र-रेखा TT’ पर होंगे,अतः TT’ स्पर्श बिन्दुपथ होगा।चूंकि TT’ दो पथों AA’ तथा BB’ के सम्पात से बना है,अतः p-विवेचक में स्पर्श बिन्दुपथ (Tac locus) द्विघातीय (quadratic) गुणनखण्ड के रूप में आना सम्भावित है।
जैसा कि चित्र से स्पष्ट है,बिन्दु P पर स्पर्श बिन्दु और वृत्तों की स्पर्श रेखाएँ भिन्न हैं।अतः स्पर्श बिन्दुपथ का समीकरण दिए हुए अवकल समीकरण का हल नहीं हो सकता।
प्रश्न:3.नोड बिन्दुपथ किसे कहते हैं? (What is Node Locus?):

उत्तर:c-विवेचक सम्बन्ध उन बिन्दुओं के बिन्दुपथ को प्रदर्शित करता है,जिनके लिए c के मान समान हों।ये c के समान मान नोड के हो सकते हैं।जो वक्र-कुल के क्रमागत वक्रों (consecutive curves) के प्रतिच्छेदन बिन्दु हो कहते हैं।इस प्रकार के बिन्दुओं के बिन्दुपथ (locus) नोड-बिन्दुपथ (Node-locus) अथवा नोड-पथ कहते हैं।अब यदि N(x,y)=0 नोड-पथ का समीकरण हो,तो यह c-विवेचक का एक गुणनखण्ड होगा,परन्तु p-विवेचक का गुणनखण्ड नहीं होगा।सामान्यतः यह दिए हुए अवकल समीकरण को संतुष्ट नहीं करता।किसी विशेष स्थिति (exceptional case) में अवकल समीकरण को संतुष्ट कर सकता है ऐसी स्थिति में नोड-पथ अन्वालोप भी होगा।
अब हम उस वक्र-कुल पर विचार करते हैं जिसके प्रत्येक वक्र का एक नोड है।यहाँ वक्र-कुल के दो क्रमागत वक्र तीन बिन्दुओं M,P तथा R में कटते हैं (देखो चित्र)।चूँकि NN’ दो पथों BB’ तथा DD’ के संपात से बना है,अतः c-विवेचक में अन्वालोप एकघातीय (Linear) तथा नोड-पथ द्विघातीय (quadratic) गुणनखण्ड के रूप में आना सम्भावित है।
जैसा चित्र से स्पष्ट है कि नोड-पथ के लिए किसी बिन्दु p का मान उसी बिन्दु पर वक्र कुल के किसी वक्र के लिए p के मान के तुल्य नहीं है।अतः नोड-पथ का समीकरण दिए गए अवकल समीकरण का हल नहीं हो सकता।
उपर्युक्त प्रश्नों के उत्तर द्वारा डिफरेंशियल इक्वेशन में विचित्र हल (Singular Solution in DE),अवकल समीकरण में विचित्र हल (Singular Solution in Differential Equations) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Singular Solution in DE
डिफरेंशियल इक्वेशन में विचित्र हल
(Singular Solution in DE)
Singular Solution in DE
डिफरेंशियल इक्वेशन में विचित्र हल (Singular Solution in DE) किसी अवकल समीकरण
का वह हल जो उसके व्यापक हल में स्वेच्छ अचर को विशिष्ट मान देने पर प्राप्त नहीं होता
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.








