Properties of Circle
1.वृत्त के गुणधर्म (Properties of Circle):
वृत्त के गुणधर्म (Properties of Circle) से पहले कुछ परिभाषाओं का अध्ययन करना आवश्यक है।
वृत्त (Circle): वृत्त एक समतल में स्थित बिन्दुओं का समुच्चय होता है जो उस समतल में दिए गए एक बिन्दु (Fixed Point) से दी हुई नियत दूरी (Constant Distance) पर होते हैं।
स्थिर बिन्दु को वृत्त का केन्द्र तथा केन्द्र से वृत्त के प्रत्येक बिन्दु की नियत दूरी को उस वृत्त की त्रिज्या कहते हैं।
वह वृत्त जिसका केन्द्र O तथा त्रिज्या r हो को सामान्यतः C(O,r) द्वारा प्रदर्शित किया जाता है।
वृत्त की जीवा तथा वृत्तखण्ड (Chord and Segment of a Circle):
जीवा (Chord):वृत्त के किन्हीं दो बिन्दुओं को मिलाने वाले रेखाखण्ड को वृत्त की जीवा कहते हैं।
व्यास (Diameter): वृत्त के केन्द्र से होकर जाने वाली जीवा को वृत्त का व्यास कहते हैं।किसी भी वृत्त के अनेक व्यास हो सकते हैं तथा व्यास वृत्त की सबसे लम्बी जीवा होती है।त्रिज्या की तरह व्यास का प्रयोग केन्द्र से होकर जाने वाली जीवा और साथ ही उसकी लम्बाई के लिए किया जाता है।
यदि d वृत्त C(O,r) का व्यास हो तो d=2r
अर्थात् वृत्त का व्यास उसकी त्रिज्या का दुगुना होता है।इससे यह भी स्पष्ट है कि एक वृत्त के सभी व्यास बराबर होते हैं।
अर्ध-वृत्त (Semi Circle):किसी भी वृत्त का व्यास,उस वृत्त को दो बराबर लम्बाई के चापों में बांटता है।इनमें से प्रत्येक चाप अर्द्धवृत्त कहलाता है। आकृति मे चाप \overset{\Large\frown}{AB} तथा चाप \overset{\Large\frown}{BA} दोनों ही अर्द्धवृत्त है। स्पष्ट है m(\overset{\Large\frown}{AB})=180^{\circ} तथा m(\overset{\Large\frown}{BA})=180^{\circ}
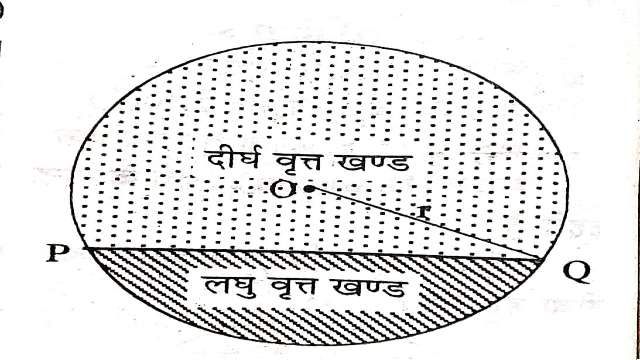
अतः हम कह सकते हैं कि चाप जिसकी लम्बाई अर्द्धवृत्त से कम हो अर्थात् जिसका डिग्री माप 180° से कम हो उसे लघुचाप कहते हैं तथा किसी चाप की लम्बाई अर्द्धवृत्त से अधिक हो अर्थात् जिसका डिग्री माप 180° से अधिक हो तो वह चाप दीर्घचाप कहलाता है।
वृत्तखण्ड (Segment):आकृति में PQ वृत्त C(O,r) की एक जीवा है।यह जीवा वृत्त से घिरे क्षेत्र (अर्थात् वृत्ताकार चकती)(disc) को दो भागों में विभाजित करती है,इन दो भागों में से प्रत्येक भाग को वृत्तखण्ड (Segment) कहा जाता है।वह वृतखण्ड जिसके संगत वृत्त का चाप लघुचाप हो,लघु वृत्तखण्ड (Minor Segment) तथा दीर्घ चाप के संगत वृत्तखण्ड दीर्घ वृत्तखण्ड (Major Segment) कहलाता है।लघु वृत्तखण्ड तथा दीर्घ वृत्तखण्ड दोनों ही एक वृत्ताकार चकती (Circular Disc) के भाग होते हैं परन्तु व्यवहार और बोलचाल में हम इन्हें प्रायः वृत्त के ही वृत्तखण्ड मान लेते हैं।
किसी वृत्तखण्ड के एकान्तर वृत्तखण्ड:
किसी वृत्त C(O,r) की किसी जीवा द्वारा विभाजित लघु तथा दीर्घ वृत्तखण्ड एक-दूसरे के एकान्तर वृत्तखण्ड कहलाते हैं।
प्रमेय (Theorem):1.वृत्त के केन्द्र से जीवा पर डाला गया लम्ब उस जीवा को समद्विभाजित करता है।
दिया है (Given): वृत्त C(O,r) की जीवा PQ पर वृत्त के केन्द्र O से डाला गया लम्ब OL है।
सिद्ध करना है (To Prove):LP=LQ
रचना (Construction):रेखाखण्ड OP तथा OQ खींचिए।
उपपत्ति (Proof):\triangle OLP तथा \triangle OLQ में
OP=OQ=r (एक ही वृत्त की त्रिज्याएं)
OL=OL (उभयनिष्ठ भुजा)
\angle OLP=\angle OLQ=90^{\circ}(दिया है)
समकोण-कर्ण-भुजा सर्वांगसमता गुणधर्म से (By RHS Congruence Property)
\triangle OLP \cong \triangle OLQ
LP=LQ (सर्वांगसम त्रिभुजों के संगत अवयव बराबर होते हैं)
प्रमेय (Theorem):2.वृत्त के केन्द्र और जीवा के मध्य बिन्दु को मिलाने वाली रेखा जीवा पर लम्ब होती है।
दिया है (Given): वृत्त C(O,r) की जीवा PQ का मध्य-बिन्दु M है।
सिद्ध करना है (To Prove):OM,जीवा PQ पर लम्ब है।
रचना (Construction):रेखाखण्ड OP तथा OQ खींचिए।
उपपत्ति (Proof): \triangle OPM तथा \triangle OQM में
PM=MQ (M,PQ का मध्य-बिन्दु है)
OP=OQ=r (एक ही वृत्त की त्रिज्याएं)
OM=OM (उभयनिष्ठ भुजा)
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (By SSS Congruence Property)
\triangle OPM \cong \triangle OQM \\ \angle OMP=\angle OMQ \cdots(1)
(सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
\angle OMP+\angle OMQ=180^{\circ} (रैखिक कोण युग्म अभिगृहीत से)
\Rightarrow \angle OMP+\angle OMP=180^{\circ} [(1) से]
\Rightarrow \angle OMP=90^{\circ}=\angle OMQ \\ \Rightarrow OM \perp PQ
अतः OM जीवा PQ पर लम्ब है।
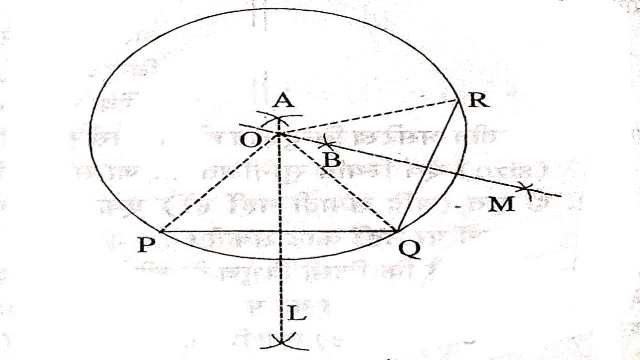
प्रमेय(Theorem):3.तीन असंरेख बिन्दुओं से होकर एक और केवल एक ही वृत्त गुजर सकता है।
दिया है (Given):तीन असंरेख बिन्दु P,Q तथा R हैं।
सिद्ध करना है (To Prove):P,Q तथा R बिन्दुओं से होकर एक और केवल एक ही वृत्त गुजर सकता है।
रचना (Construction):रेखाखण्ड PQ और QR खींचिए।PQ और QR के लम्ब समद्विभाजक क्रमशः AL और BM खींचिए।क्योंकि P,Q,R संरेख नहीं है, इसलिए AL,BM के समान्तर नहीं होगा। अतः ये एक बिन्दु पर अवश्य प्रतिच्छेद करेंगे।मान लीजिए वह बिन्दु O है।O को P,Q तथा R से मिलाइए।
उपपत्ति (Proof):O,PQ के लम्ब समद्विभाजक AL पर स्थित है।
अतः OP=OQ …….(1)
इसी प्रकार O,QR के लम्ब समद्विभाजक BM पर स्थित है।
अतः OQ=OR ………(2)
समीकरण (1) तथा (2) से-
OP=OQ=OR=r (माना)
O बिन्दु P,Q तथा R से समान दूरी पर स्थित है।
अब यदि O को केन्द्र मानकर OP त्रिज्या का एक वृत्त खींचा जाए तो वह P,Q तथा R से अवश्य गुजरेगा
\because कोई भी दो रेखाएं (लम्ब-समद्विभाजक) केवल एक ही बिन्दु O पर प्रतिच्छेद करती है।
O ही एक मात्र ऐसा बिन्दु है जो P,Q तथा R से होकर खींचा जा सकता है।
(1.)यदि तीन असंरेख बिन्दु हों तो उनसे गुजरने वाले वृत्त का माप (Size) एवं स्थिति सुनिश्चित की जा सकती है।
(2.)दो वृत्त (यदि संपाती नहीं हों) एक-दूसरे को दो से अधिक बिन्दुओं पर नहीं काट सकते।
उपर्युक्त प्रमेय से स्पष्ट है कि किसी त्रिभुज के शीर्षों से एक और केवल एक ही वृत्त गुजर सकता है।इस वृत्त को त्रिभुज का परिगत वृत्त (Circumcircle) कहते हैं।वृत्त का केन्द्र परिकेन्द्र (Circumcenrte) तथा त्रिज्या परिगत त्रिज्या (Circumradius) कहलाती है।
(3.)दो दिए गए बिन्दुओं से अनन्त संख्या में वृत्त गुजर सकते हैं।
(4.)दिए गए तीनों बिन्दु समरेखीय हों तो उनसे कोई भी वृत्त नहीं गुज़र सकता है।
(5.)किसी एक बिन्दु से अनन्त वृत्त गुजर सकते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Ratio of Areas of Similar Triangles
2.वृत्त के गुणधर्म के उदाहरण (Properties of Circle Problems):
Example:1.यदि वृत्त की त्रिज्या 13 सेमी है और इसकी एक जीवा की लम्बाई 10 सेमी हो तो इस जीवा की वृत्त के केन्द्र से दूरी ज्ञात कीजिए।
Solution:एक वृत्त जिसकी त्रिज्या की लम्बाई 13 सेमी है जिसका कि केन्द्र O है।
OA=13 सेमी,AB=10 सेमी
OL \perp AB
किसी वृत्त के केन्द्र से किसी जीवा पर डाला गया लम्ब उसे समद्विभाजित करता है।
AL=\frac{1}{2} AB=\frac{1}{2} \times 10=5 सेमी
समकोण \triangle OLA में
OA^{2}=OL^{2}+AL^{2} \\ \Rightarrow OL^{2}=OA^{2}-AL^{2} \\ =(13)^{2}-(5)^{2} \\ =169-25 \\ =144 \\ \Rightarrow OL=\sqrt{144} \\ OL=12 सेमी
अतः इस जीवा की केन्द्र से दूरी 12 सेमी है।
Example:2.एक वृत्त की दो जीवाएं AB और CD जिनकी लम्बाईयां क्रमशः 6 सेमी और 12 सेमी है, एक-दूसरे के समान्तर है तथा वे वृत्त के केन्द्र के एक ही ओर स्थित हैं।यदि AB और CD के बीच 3 सेमी की दूरी हो तो वृत्त की त्रिज्या ज्ञात कीजिए।
Solution:एक वृत्त जिसका केन्द्र O है तथा दो जीवाएं जिनकी लम्बाईयां क्रमशः 6 सेमी और 12 सेमी हैं।तथा दोनों समान्तर जीवाओं के बीच की दूरी 3 सेमी है।
रचना (Construction):OM \perp CD और OL \perp AB खींचा तथा OA व OC को मिलाया।
वृत्त के केन्द्र से किसी जीवा पर डाला गया लम्ब जीवा को समद्विभाजित करता है।
CM=\frac{1}{2} CD=\frac{1}{2} \times 12=6 सेमी
तथा AL=\frac{1}{2} AB=\frac{1}{2} \times 6=3 सेमी
OA=OC=r सेमी
माना OM=x सेमी,OL=(3+x) सेमी
समकोण \triangle OCM में
OC^{2}=OM^{2}+CM^{2} \\ \Rightarrow r^{2}=x^{2}+(6)^{2} \\ \Rightarrow r^{2}=x^{2}+36 \cdots(1)
समकोण \triangle OAL में
OA^{2}=OL^{2}+AL^{2} \\ \Rightarrow r^{2}=(3+x)^{2}+(3)^{2} \\ \Rightarrow r^{2}=9+6x+x^{2}+9 \\ \Rightarrow r^{2}=6x+x^{2}+18 \cdots(2)
समीकरण (1) व (2) से-
x^{2}+36=x^{2}+6x+18 \\ \Rightarrow 6x=36-18 \\ \Rightarrow 6x=18 \\ \Rightarrow x=\frac{18}{6} \\ \Rightarrow x=3 सेमी
x का मान समीकरण (1) में रखने पर-
r^{2}=x^{2}+36 \\ =(3)^{2}+36 \\ =9+36 \\ \Rightarrow r^{2}=45 \\ \Rightarrow r=\sqrt{45} \\ \Rightarrow r=3 \sqrt{5} सेमी
अतः वृत्त की त्रिज्या 3 \sqrt{5} सेमी है।
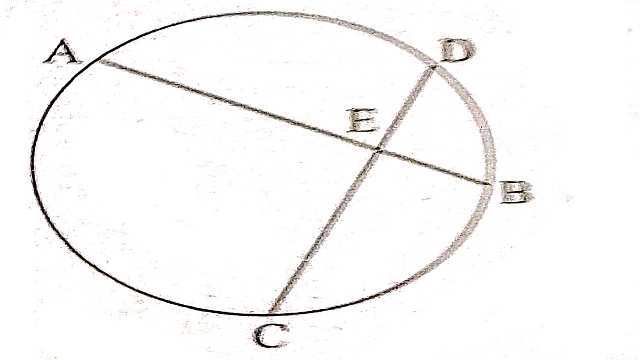
Example:3.आकृति में दो समान जीवाएं AB और CD एक दूसरे को E पर प्रतिच्छेद करती है। सिद्ध कीजिए कि \overset{\Large\frown}{AD}=\overset{\Large\frown}{CB}
Solution: दिया है (Given):जीवा AB=जीवा CD जीवा AB व CD एक-दूसरे को E पर प्रतिच्छेद करती हैं।
सिद्ध करना है (To Prove):\overset{\Large\frown}{AD}=\overset{\Large\frown}{CB}
उपपत्ति (Proof):जीवा AD=जीवा CB
[समान चाप द्वारा समान जीवा अन्तरित होती है]
लघुचाप AB=लघुचाप CD
\overset{\Large\frown}{BD} को दोनों ओर से घटाने पर-
\overset{\Large\frown}{AB} – \overset{\Large\frown}{BD} = \overset{\Large\frown}{CD} – \overset{\Large\frown}{DB}
\overset{\Large\frown}{AD} = \overset{\Large\frown}{CB}
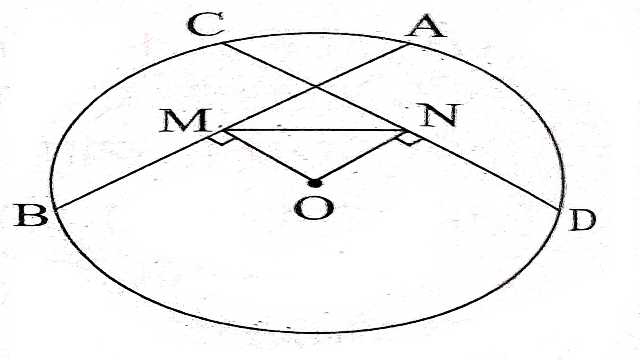
Example:4.आकृति में AB और CD एक वृत्त की समान जीवाएं हैं। वृत्त का केन्द्र O है।OM \perp AB और ON \perp CD हो तो सिद्ध कीजिए कि
Solution: दिया है (Given):AB और CD एक वृत्त की समान जीवाएं हैं। वृत्त का केन्द्र O है तथा OM \perp AB और ON \perp CD
सिद्ध करना है (To Prove):\angle OMN=\angle ONM
उपपत्ति (Proof):OM \perp AB एवं ON \perp CD
जीवा AB=जीवा CD
OM=ON ……….(1)
[समान जीवाएं केन्द्र से समान दूरी पर होती है]
\triangle OMN में
OM=ON [(1) से]
\angle OMN=\angle ONM [समान भुजा के सामने के कोण समान होते हैं]
अतः \angle OMN=\angle ONM
Example:5.आकृति में O और O’ दिए गए वृत्तों के केन्द्र हैं। AB \parallel OO^{\prime} हैं।सिद्ध कीजिए कि AB=2OO’.
Solution: दिया है (Given):O^{\prime} E \perp BC और OD \perp AC \\ O^{\prime} E \perp BC
BE=CE
(केन्द्र से जीवा पर डाला गया लम्ब जीवा को समद्विभाजित करता है)
BE=2CE ………(1)
पुनः OD \perp AC
CD=DA
AC=2CD …….(2)
समीकरण (1) एवं (2) को जोड़ने पर-
BC+AC=2CE+2CD \\ \Rightarrow AB=2(CE+CD) \\ \Rightarrow AB=2DE ……..(3)
O^{\prime} E \perp AB और OD \perp AB \\ O^{\prime} E \parallel OE
और O^{\prime} E \parallel OE ( \because OO^{\prime} \parallel AB )
\therefore OO’ED एक समान्तर चतुर्भुज है।
OO’=DE ……..(4)
(समान्तर चतुर्भुज की सम्मुख भुजा समान होती है)
समीकरण (3) और (4) से-
AB=2OO’ (OO’=DE)
उपर्युक्त उदाहरणों के द्वारा वृत्त के गुणधर्म (Properties of Circle) को समझ सकते हैं।
3.वृत्त के गुणधर्म की समस्याएं (Properties of Circle Problems):
(1.)आकृति में एक वृत्त C(O,5)है।AB और CD वृत्त की जीवाएं हैं। यदि OP \perp AB ,OQ \perp CD ,AB \parallel CD ,AB=6 सेमी तथा CD=8 सेमी हो तो PQ का मान ज्ञात कीजिए।
(2.)एक वृत्त की दो जीवाएं AB और AC बराबर है। सिद्ध कीजिए कि वृत्त का केन्द्र \angle BAC के समद्विभाजक पर स्थित होगा।
(3.)एक वृत्त की दो जीवाएं PQ और RS समान्तर हैं और AB जीवा PQ का लम्ब समद्विभाजक है। कोई रचना किए बिना सिद्ध कीजिए कि AB जीवा RS की समद्विभाजक है।
(4.) सिद्ध कीजिए कि एक समबाहु त्रिभुज के केन्द्रक (Centroid) और परिवृत्त का केन्द्र (परिकेन्द्र) (Circumcenrte) संपाती होते हैं।
(5.) सिद्ध कीजिए कि किसी वृत्त की दो समान्तर जीवाओं के मध्य बिन्दुओं को मिलाने वाली रेखा वृत्त के केन्द्र से जाती है।
उत्तर (Answers):
(1.)PQ=1सेमी
उपर्युक्त सवालों को हल करने पर वृत्त के गुणधर्म (Properties of Circle) को ठीक से समझ सकते हैं।
Also Read This Article:-Pythagoras Theorem
4.वृत्त के गुणधर्म (Properties of Circle) के बारे में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.आप एक सर्कल को कैसे परिभाषित करते हैं? (How do you define a circle?):
उत्तर:परिभाषा:एक वृत्त एक समतल में सभी बिंदुओं का समूह होता है जो किसी दिए गए बिंदु से समान दूरी पर होता है जिसे वृत्त का केंद्र कहा जाता है।हम एक वृत्त का प्रतिनिधित्व करने के लिए प्रतीक ⊙ का उपयोग करते हैं।वृत्त के केंद्र से वृत्त के किसी भी बिंदु तक एक रेखा खंड वृत्त की त्रिज्या है।
गणित या ज्यामिति में,एक वृत्त एक विशेष प्रकार का दीर्घवृत्त होता है जिसमें उत्केन्द्रता शून्य होती है और दोनों नाभियाँ संपाती होती हैं।वृत्त एक द्वि-आयामी आकृति है, जिसका क्षेत्रफल और परिमाप है।वृत्त की परिमाप को परिधि भी कहा जाता है,जो कि वृत्त के चारों ओर की दूरी है।
प्रश्न:2.मैं एक वृत्त का क्षेत्रफल कैसे ज्ञात करूं? (How do I figure out area of a circle?):
उत्तर:एक वृत्त का क्षेत्रफल त्रिज्या के वर्ग (A = π r²) का π गुना होता है।
प्रश्न:3.वृत्त कितने प्रकार के होते हैं? (What are the types of circle?):
उत्तर: वृत्तों के प्रकार – संकेंद्रित वृत्त (Concentric circles),वृत्तों का संपर्क (Contact of circles),ओर्थोगोनल वृत्त (Orthogonal circles)।
प्रश्न:4.वृत्त क्या है और इसका सूत्र क्या है? (What is circle and its formula?):
उत्तर:वृत्त सूत्र एक वृत्त के व्यास के रूप में व्यक्त किए जाते हैं।D = 2 × r।एक वृत्त की परिधि।C = 2 ×π × r।
प्रश्न:5.सर्कल के अवयव क्या हैं? (What are the elements of circle?):
उत्तर:महत्वपूर्ण वृत्त के भाग
त्रिज्या: वृत्त के केंद्र से उसके बाहरी रिम तक की दूरी।
जीवा: एक रेखा खंड जिसका प्रारंभ और समापन बिंदु एक वृत्त पर होता है।
व्यास:एक जीवा जो वृत्त के केंद्र से होकर गुजरती है।
छेदक रेखा: एक रेखा जो एक वृत्त को दो बिंदुओं में काटती है।
प्रश्न:6.सर्कल के 5 गुण क्या हैं? (What are the 5 properties of a circle?):
उत्तर:वृत्त के गुण
वृत्तों की समान त्रिज्या होने पर सर्वांगसम कहा जाता है।
वृत्त का व्यास किसी वृत्त की सबसे लंबी जीवा है।
समान जीवा और समान वृत्त की परिधि समान होती है।
जीवा पर लंबवत खींची गई त्रिज्या जीवा को समद्विभाजित करती है।
अलग-अलग त्रिज्या वाले वृत्त असमान होती हैं.
प्रश्न:7.वृत्त कक्षा 10 क्या है? (What is a circle Class 10?):
उत्तर:वृत्त: एक वृत्त एक समतल में सभी बिंदुओं का एक संग्रह है जो एक निश्चित बिंदु से एक अचर दूरी पर होते हैं।
केंद्र:निश्चित बिंदु को केंद्र कहा जाता है।
त्रिज्या:केंद्र से नियत दूरी को त्रिज्या कहते हैं। जीवा:वृत्त पर किन्हीं दो बिंदुओं को मिलाने वाले रेखाखंड को जीवा कहते हैं।
प्रश्न:8.किसी भी वृत्त में सबसे लंबी जीवा कौन सी है? (What is the longest chord in any circle?):
उत्तर:व्यास
वृत्त-वृत्त
जीवाएँ केंद्र से समान दूरी पर होती हैं यदि और केवल यदि उनकी लंबाई समान हो।समान जीवाओं को वृत्त के केंद्र से समान कोणों द्वारा अंतरित किया जाता है।एक वृत्त के केंद्र से गुजरने वाली जीवा को व्यास कहा जाता है और यह उस विशिष्ट वृत्त की सबसे लंबी जीवा होती है।
प्रश्न:9.गणित में एक पूर्ण वृत्त क्या है? (What is a perfect circle in math?):
उत्तर:एक वृत्त के पूर्ण होने के लिए,हमें निश्चित रूप से जानने के लिए वृत्त की परिधि के चारों ओर अनंत संख्या में बिंदुओं को मापने की आवश्यकता होगी।प्रत्येक बिंदु को कण स्तर से आणविक स्तर तक सटीक होना चाहिए,चाहे वृत्त स्थिर हो या गति में हो,जो पूर्णता को निर्धारित करना एक मुश्किल उपलब्धि बनाता है।
प्रश्न:10.सर्कल प्रमेय क्या है? (What is circle theorem?):
उत्तर:वृत्तों में अलग-अलग कोण गुण होते हैं जिनका वर्णन अलग-अलग वृत्त प्रमेयों द्वारा किया जाता है।वृत्त प्रमेयों का उपयोग ज्यामितीय प्रमाणों और कोणों की गणना के लिए किया जाता है।
प्रश्न:11.6 मुख्य वृत्त प्रमेय क्या हैं? (What are the 6 main circle theorems?):
उत्तर:वृत्त प्रमेय 1 – केंद्र में कोण।
वृत्त प्रमेय 2 – अर्धवृत्त में कोण।
वृत्त प्रमेय 3 – एक ही वृत्तखंड में कोण।
वृत्त प्रमेय 4 – चक्रीय चतुर्भुज।
वृत्त प्रमेय 5 – त्रिज्या से स्पर्शरेखा तक।
वृत्त प्रमेय 6 – एक बिंदु से एक वृत्त पर स्पर्श रेखाएँ।
वृत्त प्रमेय 7 – एक बिंदु से एक वृत्त पर स्पर्शरेखाएं II।
प्रश्न:12.वृत्त प्रमेय 4 क्या है? (What is circle theorem 4?):
उत्तर:चक्रीय चतुर्भुज में विपरीत कोण समतल पदों में जुड़ते हैं (add up to in plain terms): यदि आप चक्रीय चतुर्भुज (एक चार भुजा वाली आकृति जहां चार शीर्ष एक वृत्त की परिधि को स्पर्श करते हैं) को नीचे देखते हैं,तो प्रत्येक शीर्ष वृत्त की परिधि पर एक बिंदु होता है।
प्रश्न:13.एक वृत्त के 8 प्रमेय क्या हैं? (What are the 8 theorems of a circle?):
उत्तर:पहला वृत्त प्रमेय -केंद्र और परिधि पर कोण। दूसरा वृत्त प्रमेय -अर्धवृत्त में कोण। तीसरा वृत्त प्रमेय-एक ही खंड में कोण।चौथा वृत्त प्रमेय – चक्रीय चतुर्भुज में कोण।
प्रश्न:14.सात वृत्त प्रमेय क्या हैं? (What are the seven circle theorems?):
उत्तर:विशेष रूप से,छह वृत्तों की एक श्रृंखला दी गई है,जो सातवें वृत्त की सभी स्पर्शरेखा और उसके दो पड़ोसियों के लिए प्रत्येक स्पर्शरेखा है,सातवें वृत्त पर स्पर्शरेखा के बिंदुओं के विपरीत युग्मों के बीच खींची गई तीन रेखाएं सभी एक ही बिंदु से होकर गुजरती हैं।(Specifically, given a chain of six circles all tangent to a seventh circle and each tangent to its two neighbors, the three lines drawn between opposite pairs of the points of tangency on the seventh circle all pass through the same point.)
उपर्युक्त प्रश्नों के उत्तर द्वारा वृत्त के गुणधर्म (Properties of Circle) के बारे में जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
