Overview of fundamental mathematics functions through graphs
Overview of fundamental mathematics functions through graphs
- इंटरैक्टिव रेखांकन के माध्यम से मौलिक गणित फलनों का अवलोकन (Overview of fundamental mathematics functions through graphs) में ग्राफ के महत्त्व को बताया गया है.Sawyer के शब्दों में:प्रत्येक अध्यापक के समक्ष आज यह समस्या है कि तथ्यों को इस प्रकार कैसे प्रस्तुत किया जाय जिससे छात्र स्वत: लालायित होकर उनकोसमझें.हम एक घिसा-पिटा कथन जल्दी ही भूल जाते हैं.स्पष्ट चित्रावलियाँ लम्बे समय तक याद रहती हैं.इतिहास की कोई पुस्तक पढ़्ने तथा इतिहास की कोई फिल्म देखने में बहुत अंतर होगा.फिल्म के माध्यम से हम घटनाओं को आत्मसात करते हैं तथा उन्हें अधिक समय तक याद भी रखते हैं.
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
1.इंटरैक्टिव रेखांकन के माध्यम से मौलिक गणित फलनों का अवलोकन (Overview of fundamental mathematics functions through interactive graphs),रेखांकन के माध्यम से मौलिक गणित फलनों का अवलोकन (Overview of fundamental mathematics functions through graphs):
- हम सभी किसी न किसी गणितीय कार्य के विचार से अवगत हुए हैं। अधिकांश समय, यह अवधारणा दिमाग में विशिष्ट रूप से बीजगणित से जुड़ी हो सकती है या केवल कुछ गूढ़ सूत्रों से भी जुड़ी हो सकती है। हम कुछ मूलभूत कार्यों का एक छोटा सा दौरा करने जा रहे हैं और उन्हें इंटरएक्टिव रेखांकन का उपयोग करके अमूर्त दुनिया से व्यक्त करने का प्रयास करते हैं।
- मैथ्स मॉडल और रिश्ते बनाने के लिए बनाए गए नियमों का उपयोग करते हैं, ग्राफ मॉडल का उपयोग करने से समझने में मदद मिलेगी:
एक मॉडल किस संबंध का प्रतिनिधित्व करता है?
क्या वास्तविक दुनिया आइटम एक रिश्ता साझा करते हैं?
क्या कोई रिश्ता हमारे लिए मायने रखता है?
उन लोगों के लिए जो स्वाभाविक रूप से बीजगणितीय और ज्यामितीय दुनिया दोनों में कार्यों को व्यक्त कर सकते हैं, हम आशा करते हैं कि आप पुरानी गणितीय यादों से एक ताज़ा पाएंगे।
Also Read This Article:Set theory and basic notation part-2
2.रैखिक (Linear):
- रैखिक समीकरण समीकरण का सबसे सरल रूप है जिससे आप निपट सकते हैं; यह समस्या को एक अनजान अज्ञात चर (आमतौर पर x) और कोई प्रतिपादक (उदा। f (x) = \frac{2x^{2} }{15}) तक सीमित करता है।
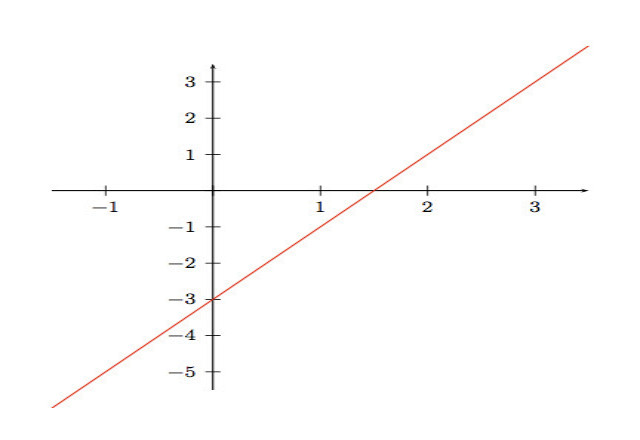
इस तरह के समीकरण का सामान्य रूप है: f (x) = ax + b - किसी भी रेखीय अभिव्यक्ति को 2 डी ग्राफिक में एक रेखा के रूप में खींचा जा सकता है। ग्राफ ड्राइंग बहुत सरल है: हमारे पास y, या f (x), ऊर्ध्वाधर अक्ष (परिणाम) पर और x मानों की एक श्रृंखला के लिए (क्षैतिज एब्ससिस) हम बिंदुओं (x, y) की गणना और दर्शाते हैं।
- जानने के लिए मूल पंक्ति: y = x (सभी x, y समान मान के लिए)।
यहाँ ड्राइंग y = 2x - एक्स को एक स्थिरांक से गुणा करना रेखा पर एक घुमाव बना रहा है।
यहां चित्र y = 2x – 3 एक स्थिर मान द्वारा अभिव्यक्ति को जोड़ना या घटाना सिर्फ एक ऑफसेट जोड़ना है।
- संक्षेप में:ए बदलने से लाइन की ढलान बदल रही है।बदल रहा है बी लाइन के ऑफसेट बदल रहा है।
Also Read This Article:Graph of a function
3.द्विघात (Quadratic):
- द्विघात समीकरण रेखीय समीकरण से सिर्फ एक कदम आगे हैं, हम अभी भी समस्या को एक अनजान अज्ञात चर (आमतौर पर add x ’) तक सीमित रखते हैं और एक शब्द जोड़ते हैं: x² (या x * x)। ऐसे समीकरण का सामान्य रूप है:
f (x) = ax² + bx + c, जहाँ a! = 0 - वे अक्सर कई क्षेत्रों में बदल जाते हैं और अक्सर भौतिक विज्ञान, खगोल विज्ञान, इंजीनियरिंग, कंप्यूटिंग, वास्तुकला के क्षेत्र में वास्तविक दुनिया की अधिकांश समस्याओं के भीतर समग्र समाधान के हिस्से के रूप में एक उपस्थिति बनाते हैं …
- चलो इसे ऑनलाइन खेलते हैं और हम जल्दी से देखेंगे कि: परिवर्तन करने से परबोला का उद्घाटन बदल रहा है। बदलते बी x = 0. परवलय के ढलान को बदल रहा है। सी बदलने से परबोला की ऑफसेट बदल रहा है।
4.रूपान्तरण (Translation):
- ज्यामिति में परिवर्तनों की तरह, हम किसी गणितीय वस्तु को उसके कार्य को बदलकर उसका अनुवाद / बदलाव कर सकते हैं।
- पहले से ही पिछले मॉडल (रैखिक, द्विघात) के साथ देखा जाता है, हम इसे फंक्शन में निरंतर जोड़कर ऊपर या नीचे ले जा सकते हैं:
f (x) → f (x) + b - इसे बाएं या दाएं स्थानांतरित करने के लिए, हम फ़ंक्शन चर (x-value) में एक स्थिरांक जोड़ते हैं:
f (x) → f (x + a) हम इसे “अनुपस्थिति मूल” के रूप में आगे बढ़ने या थोड़ा देर से आगे बढ़ने के बारे में सोच सकते हैं।
इसे एक साथ रखना:
f (x) → f (x + a) + b
- वेरिएबल में पॉजिटिव नंबर जोड़ने से फंक्शन बाईं ओर चला जाता है (नकारात्मक दिशा)?
- अच्छी तरह से कल्पना करें कि आप समारोह के साथ रात 8:00 बजे एक फिल्म की रिकॉर्डिंग शुरू करना चाहते हैं: प्रारंभ (t) = 8:00 बजे। यदि आप यह कहने के लिए अपना मन बदलते हैं कि हम 5 मिनट पहले रिकॉर्ड करना चाहते हैं, तो हमारे पास फ़ंक्शन होगा: प्रारंभ (t + 5 मिनट) = 8:00 बजे
- वर्तमान समय में 5 मिनट जोड़ने से रिकॉर्ड 5 मिनट पहले (यानी बाईं दिशा में) शुरू हो जाएगा। यह एक नियुक्ति के लिए हमारी घड़ी को अग्रिम में रखना पसंद है।
Also Read This Article:What is mathematical reality and truth
5.स्केलिंग (खिंचाव / संपीड़ित)[Scaling (Stretch / Compress)]:
- यदि हम ऊपर दिए गए रैखिक और अनुवाद कार्यों को समझते हैं, तो हम कल्पना कर सकते हैं कि स्केलिंग फ़ंक्शन क्या हो सकता है: परिवर्धन के साथ खेलने के बजाय, हम अपनी गणितीय वस्तु को खींचने या संपीड़ित करने के लिए गुणन कारकों के साथ खेलेंगे। कृपया ध्यान दें कि एक पैमाना गैर-कठोर परिवर्तन है: यह ग्राफ फ़ंक्शन के आकार और आकार को बदल देता है।
- हम पूरे फ़ंक्शन को एक स्थिर से गुणा करके इसे y-दिशा में खींच या संकुचित कर सकते हैं:
f (x) → a * f (x)
- हम फंक्शन चर x को एक स्थिरांक से गुणा करके x- दिशा में खींच या संकुचित कर सकते हैं:
f (x) → f (b * x)
इसे एक साथ रखना :
f (x) → a * f (b * x) - मुझे यकीन है कि अब आप सोच सकते हैं कि बड़े बी मूल्य एक्स-स्केल पर अधिक संपीड़न का कारण क्यों बनते हैं।
हम कह सकते हैं: हम एक ही आधार इकाई के भीतर अधिक जानकारी रखते हैं।
6.प्रतिलोम -विरोधी फलन -रिवर्स -प्रतिबिंबित (Inverse — Anti-function — Reverse — Reflect):
- आमतौर पर लिखित एफ -1 (एक्स), वे समीकरणों को हल करने के लिए बेहद उपयोगी होते हैं और इसलिए कई अवधारणाओं को व्यक्त करने के लिए एक बहुत ही दिलचस्प उपकरण हैं। वे गणितीय कार्यों को उलटने की अनुमति देते हैं (जैसे माइनस व्युत्क्रम राशि, गुणा गुणन मंडल, लॉगरिदम व्युत्क्रम घातीय आदि) को उलट देते हैं। जब भी कोई गणितीय प्रक्रिया शुरू की जाती है, तो सबसे महत्वपूर्ण प्रश्नों में से एक यह है कि इसे उलटा कैसे किया जाए।
- दो कार्य एक दूसरे के व्युत्क्रम हैं यदि वे निम्नलिखित अर्थों में “एक दूसरे को पूर्ववत करें”: यदि एक के आउटपुट को दूसरे के इनपुट के रूप में उपयोग किया जाता है, तो यह मूल इनपुट के परिणामस्वरूप होता है।
- हम सभी स्वाभाविक रूप से बुनियादी कार्यों और उनके व्युत्क्रम के एक टन को जानते हैं, यहाँ कुछ ऐसे हैं जो आप पर हो सकते हैं:
f (x) = 2 * x, f ^ {- 1} (x) = {x}{2}
f (x) = x², f ^ {- 1} (x) =\sqrt{x}
f (x) = cos (x), f ^ {- 1} (x) = arccos (x)
f (x) = ln (x), f ^ {- 1} (x) = e^x
समरूपता दिखाती एक रचना। - F-1 (x) का ग्राफ x और y axes के पदों को स्विच करके f के ग्राफ से प्राप्त किया जा सकता है: यह रेखा y = x के पार ग्राफ को दर्शाने के बराबर है।
- उलटा के बारे में अच्छी बात यह है कि हम केवल परिणाम के साथ मूल मूल्य पर वापस लाने में सक्षम हैं। जब फ़ंक्शन एफ (दरवाजा) उदाहरण के लिए एक खुले दरवाजे को बंद कर देता है, तो उलटा फ़ंक्शन एफ -1 (दरवाजा) इसे वापस खोलने के लिए बदल देता है। वे समीकरण समान विचार व्यक्त करते हैं:
f (x) = y यदि और केवल तभी f ^ {- 1} (y) = x
f ^ {- 1} (f (x)) = x \text{ और } f (f ^ {- 1} (x)) = x
7.अवकलन -अवकल्ज (Differentiation — Derivative):
- एक सीधी रेखा के विपरीत, एक वक्र का ढलान लगातार बदलता रहता है जैसा कि आप ग्राफ के साथ चलते हैं। एक पहाड़ पर लंबी पैदल यात्रा के लिए तैयार होने की कल्पना करें: वक्र स्वयं पहाड़ है और हम यह जानना चाहते हैं कि ढलान को संभालने के लिए क्या होगा और जब हम अपना शिविर बनाने के लिए रुक सकते हैं (उम्मीद है कि जब फ्लैट होने के लिए कोई ढलान नहीं है)।
- इस ढलान फ़ंक्शन को प्राप्त करने के लिए, गणित के पास इसका सबसे अद्भुत उपकरण है: भेदभाव। किसी फ़ंक्शन के व्युत्पन्न का पता लगाने के लिए भेदभाव का उपयोग किया जाता है और यह व्युत्पन्न, लिखित f ‘(x), सटीक फ़ंक्शन है जो ढलान के विकास का वर्णन करता है। इसका उपयोग कई चीजों को खोजने के लिए किया जाता है, जैसे कि किसी फंक्शन का एक्स्ट्रेमा या ट्रेजेक्ट्रीज़ का वर्णन (जब यह कैसे और कैसे तेज / घट रहा है) और हम जल्द ही इसके बारे में एक पूरा कोर्स लिखने के लिए उत्साहित हैं।
- हरे (पहाड़) में एक वक्र f (x) और नीले रंग में इसका ढलान विकास x (व्युत्पन्न) दिखाता है:
f (x) = 0.2x^{3} + x^{2} - 2
f ‘(x) = 0.6x² + 2x - ढलान के विकास को सीधे हमारे फ़ंक्शन के विकास के साथ पढ़ा जा सकता है जो बहुत आसान है! हम निम्नलिखित दिलचस्प जानकारी सेकंड में देख सकते हैं:
A एक विलोम है, जब f का ढलान 0 (यह फ्लैट) के बराबर है। A तब इसके व्युत्पन्न पर बिंदु है (ढलान के रूप में, f ‘= 0)
B ‘वह बिंदु है जब f’ अपने न्यूनतम स्थान पर है: यह वह जगह है जहां ढलान सबसे नीचे जाता है।
C, C ‘पर हम दूसरी एक्सट्रैमा देखते हैं: A, A’ के समान अवलोकन।
एक रेखांकन कैलकुलेटर का उपयोग स्वचालित रूप से हमारे व्युत्पन्न की गणना और साजिश करेगा, यह हमारी समस्याओं के समाधान की कल्पना और जांच करने के लिए एक अद्भुत उपकरण है।
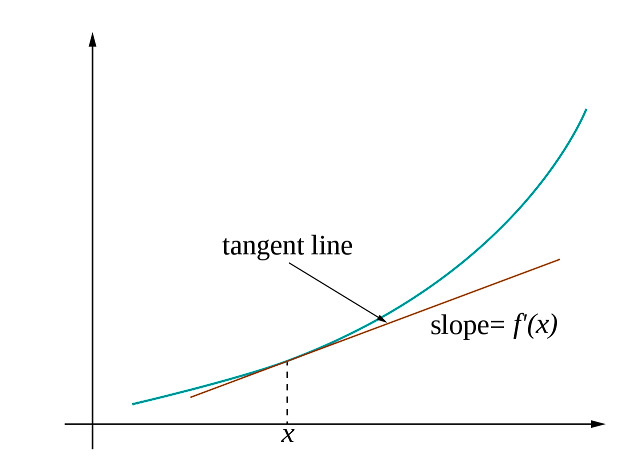
8.स्पर्शरेखा (Tangent Line):
- वक्र के एक बिंदु पर स्पर्शरेखा रेखा सीधी रेखा (रैखिक कार्य) है जो उस बिंदु से गुजरती है और इस बिंदु पर वक्र के समान ढलान है। जबकि स्पर्शरेखा रेखा की गणना प्रत्येक बिंदु पर ढलान की गणना करके की जा सकती है, यह “सौभाग्य से” हमारे व्युत्पन्न f का प्रत्यक्ष उत्पाद है (x):
- स्पर्शरेखा {{रेखा} (x) = f ‘(a) (x-a) + f (a)
स्पर्शरेखा रेखा के रैखिक समीकरण को निम्न पर पढ़ा जा सकता है: tangent_ {line} (x) = ax + b
- – स्थिर a f ‘(a) है: बिंदु A पर वक्र का ढलान।
– स्थिर b f (a) है: बिंदु A पर वक्र का मान (इसकी भरपाई)।
– चर x (x – a) है: हमने बस स्पर्शरेखा रेखा के अनुपस्थिति मूल को बिंदु A (cf. ऊपर अनुवाद) में स्थानांतरित कर दिया है।
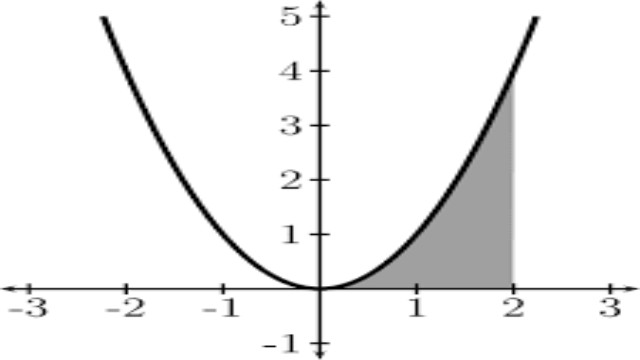
9.समाकलन -इंटीग्रल (Integration — Integral):
- एकीकरण अपने विलोम ऑपरेशन के साथ पथरी के दो मुख्य ऑपरेशनों में से एक है: भेदभाव। इंटीग्रल, गणित में, कुछ अंतराल (निश्चित अभिन्न) के लिए एक फ़ंक्शन के वक्र (एब्सिस्सा और ग्राफ के बीच क्षेत्र) के बराबर एक संख्यात्मक मान है या एक फ़ंक्शन एफ (x) व्युत्पन्न (अनिश्चित अभिन्न) के विपरीत है। : अभिन्न का पता लगाना एक व्युत्पत्ति खोजने का विलोम है, इसीलिए इसे विरोधी व्युत्पन्न भी कहा जाता है।
- यहां जिन इंटीग्रल्स का चित्रण किया गया है, वे उन निश्चित इंटीग्रल्स को कहते हैं: दो अंक ए और बी (बंद अंतराल) के बीच वक्र के नीचे क्षेत्र के बराबर एक संख्यात्मक मूल्य और द्वारा दिया जाता है:
- दूसरे शब्दों में, स्थिरांक कोई भी क्षेत्र ऑफसेट हो सकता है जो बिंदु A से पहले मौजूद हो सकता है और इसलिए बिंदु B, निश्चित अभिन्न घटाव के दौरान इस मात्रा को रद्द कर देता है: F (b) – F (a)
- उपर्युक्त आर्टिकल में इंटरैक्टिव रेखांकन के माध्यम से मौलिक गणित फलनों का अवलोकन (Overview of fundamental mathematics functions through graphs) के बारे में बताया गया है.
Overview of fundamental mathematics functions through graphs
इंटरैक्टिव रेखांकन के माध्यम से मौलिक गणित फलनों का अवलोकन
(Overview of fundamental mathematics functions through graphs)
Overview of fundamental mathematics functions through graphs
इंटरैक्टिव रेखांकन के माध्यम से मौलिक गणित फलनों का अवलोकन (Overview of fundamental mathematics functions through graphs)
में ग्राफ के महत्त्व को बताया गया है.के शब्दों में:प्रत्येक अध्यापक के समक्ष आज यह समस्या है कि तथ्यों को
इस प्रकार कैसे प्रस्तुत किया जाय जिससे छात्र स्वत: लालायित होकर उनकोसमझें.
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |