Median and Simple Arithmetic Mean
1.मध्यका और सरल समान्तर माध्य (Median and Simple Arithmetic Mean),अज्ञात मूल्य अथवा आवृत्ति का निर्धारण (Determination of Unknown Value or Frequency):
मध्यका और सरल समान्तर माध्य (Median and Simple Arithmetic Mean) के इस आर्टिकल में मध्यका,समान्तर माध्य और अज्ञात मूल्य अथवा अज्ञात आवृत्ति ज्ञात करके सवालों को समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Median and Average in Statistics
2.मध्यका और सरल समान्तर माध्य के साधित उदाहरण (Median and Simple Arithmetic Mean Solved Examples):
Example:72.निम्नलिखित सारणी में प्रस्तुत समंकों से पतियों एवं पत्नियों की औसत आयु की गणना कीजिए:
(From the data given in the following table calculate the average ages of husbands and wives.)

Solution:Calculation Table of Mean

पतियों की आयु का समान्तर माध्य \overline{X}=A+\frac{\Sigma d x}{N} \times i \\ =32.5+\frac{16}{100} \times 5 \\ =32.5+\frac{380}{100} \\ =32.5+3.8 \\ \overline{X} =36.3
पत्नियों की औसत आयु (\overline{Y})=A+\frac{\Sigma d y}{N} \times i \\ =32.5-\frac{33}{100} \times 5 \\ =32.5-\frac{165}{100} \\ =32.5-1.65 \\ \Rightarrow \bar{Y}=30.85
Example:73.आय वितरण के निम्न समंकों से समान्तर माध्य व मध्यका का परिकलन कीजिए।यह दिया गया है कि अधिकतम आय वर्ग में व्यक्तियों की कुल आय 435 रु. है तथा 20 रु. से कम आय किसी भी व्यक्ति की नहीं है:
(From the following data of income distribution,calculate the Arithmetic Mean and the Median.It is given that the total income of persons in the highest income group is Rs. 435 and none is earning less than Rs. 20):

Solution:Calculation Table of Mean and Median
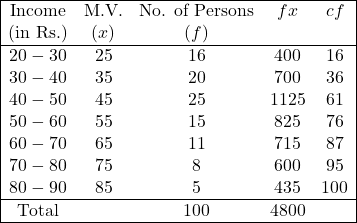
पद विचलन रीति से (From Step Deviation Method)
समान्तर माध्य (Mean) (\overline{X})=\frac{\Sigma f x}{N} \\=\frac{4800}{100} \\ \Rightarrow \overline{X}=48
मध्यका (Median) m=\frac{N}{2}=\frac{100}{2}=50
अतः 50 संचयी आवृत्ति 61 में सम्मिलित है अतः मध्यका वर्ग 40-50 है।
l_1=40,f=25, c=36, i=50-40=10
मध्यका (M)=1_{1}+\frac{i}{f}(m-c) \\=40+\frac{10}{25}(50-36) \\ =40+\frac{2}{5}(14) \\ =40+5.6 \\ \Rightarrow M =45.6
Example:74.निम्न सारणी में एक फैक्ट्री में कार्यरत 100 श्रमिकों की साप्ताहिक औसत मजदूरी का विवरण प्रस्तुत है,जिनके आधार पर निम्नलिखित का परिकलन कीजिए:
(The following table gives the distribution of the average weekly wages of 100 workers in a factory.Calculate the following):
(i)The most frequent average weekly wages of the workers.
(ii)The total weekly wages of the workers.
(iii)The weekly wages of a worker whose wages are greater than that of 75% of workers.

Solution:Calculation Table of Mode,Mean and Median

(i)निरीक्षण द्वारा बहुलक वर्ग 35.5-40.5 है
l_1=35.5, f_0=23, f_1=31, f_2=40.5-35.5=5 \\ \Delta_1=f_1-f_0=31-23=8 \\ \Delta_2=f_1-f_2=31-11=20
बहुलक (Z)=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i \\ =35.5+\frac{8}{8+20} \times 5 \\ =35.5+\frac{40}{28} \\ =35.5+1.428 \\ =36.928 \\ \Rightarrow Z \approx 36.93
समूहीकरण द्वारा बहुलक

उपर्युक्त विश्लेषण से स्पष्ट है कि 35.5-40.5 वर्ग 6 बार (सबसे अधिक बार) आवृत्त होता है जो बहुलक वर्ग है।अतः निरीक्षण तथा समूहीकरण दोनों से बहुलक समान है।
Z \approx 36.93
(ii)Total weekly wage of the workers
=A \times N+f d x^{\prime} \times i \\ =38 \times 100-30 \times 5 \\ =3800-150 \\ =3650
(iii)75% से अधिक साप्ताहिक मजदूरी के लिए P_{76} ज्ञात करना होगाः
P_{76}=\frac{76 N}{100}=\frac{76 \times 100}{100}=76
76 संचयी आवृत्ति 86 में सम्मिलित है जिसका वर्ग 40.5-45.5 है।अतः
l_1=40.5, i=45.5-40.5=5, f=11, C=75 \\ P_{76}=l_1+\frac{i}{f}\left(p_{76}-c\right) \\ =40.5+\frac{5}{11}(76-75) \\ =40.5+\frac{5}{11} \times 1 \\ =40.5+0.4545 \\ =40.9545 \\ \Rightarrow P_{76} \approx 40.95
Example:75.एक फर्म के 1000 कर्मचारियों में से 10 प्रतिशत कर्मचारी 5 रु. प्रतिदिन से कम अर्जित करते हैं,200 कर्मचारी 5 रु. से 9.99 रु. प्रतिदिन,30 प्रतिशत कर्मचारी 15 रु. से 19.99 रु. प्रतिदिन और शेष कर्मचारी 20 रु. या इससे अधिक वेतन प्राप्त करते हैं।मध्यका मजदूरी क्या है?
(10 percent of the workers in a firm employing a total of 1000 workers earn less than Rs. 5 per day,200 earn between Rs. 5 and 9.99,30 percent between 10 and 19.99,250 workers between 15 and 19.99 and the rest 20 and above.What is the median wage?)
Solution:5 रु. प्रतिदिन से कम अर्जित कर्मचारियों की संख्या=1000 \times \frac{10}{100}=100
5 रु. से 9.99 रु. प्रतिदिन अर्जित करने वाले कर्मचारियों की संख्या=200
10 रु. से 14.99 रु. प्रतिदिन अर्जित करने वाले कर्मचारियों की संख्या=1000 \times \frac{30}{100}=300
15 रु. से 19.99 रु. प्रतिदिन अर्जित करने वाले कर्मचारियों की संख्या=150
यह समावेशी श्रेणी है।अतः हल करने से पूर्व इसे अपवर्जी श्रेणी में निम्न प्रकार प्रस्तुत करना होगा:
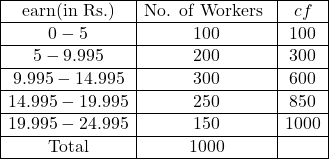
m=\frac{N}{2}=\frac{1000}{2}=500
500 संचयी आवृत्ति 600 में सम्मिलित है अतः मध्यका वर्ग 9.995-14.995 है।
l_1=9.995, i=14.995-9.995=5, f=300, c=300
मध्यका (M)=l_1+\frac{i}{f}(m-c) \\ =9.995+\frac{5}{300}(500-300) \\ =9.995+\frac{1}{60} \times 200 \\ =9.995+3.3333 \\ =13.3283 \\ \Rightarrow M \approx 13.328
Example:91.निम्नलिखित अपूर्ण आवृत्ति बंटन में अज्ञात आवृत्तियों का मान ज्ञात कीजिए यदि मध्यका 27 तथा बहुलक 26 हो:
(Find out the missing frequencies in the following incomplete frequency distribution if median is 27 and mode 26):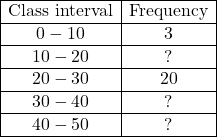
Solution:Assume the frequency of the class 10-20 be x and 40-50 be y.
Calculation Table of Missing Frequency

प्रश्नानुसार बहुलक 26 तथा मध्यका 27 है तो बहुलक तथा मध्यका वर्ग दोनों ही 20-30 होगा।
l_1=20, f_1=20, f_0=x, f_2=12, i=30-20=10 \\ \Delta_1=f_1-f_0=20-x \\ \Delta_2=f_1-f_2=20-12=8
बहुलक Z=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i \\ 26=20+\frac{20-x}{20-x+8} \times 10 \\ \Rightarrow 26-20=\frac{200-10 x}{28-x} \\ \Rightarrow 6(28-x)=200-10 x \\ \Rightarrow 168-6 x=200-10 x \\ \Rightarrow 10 x-6 x=200-168 \\ \Rightarrow 4 x=32 \\ \Rightarrow x=\frac{32}{4}=8
मध्यका (Median): m=\frac{N}{2}=\frac{35+x+y}{2}
मध्यका वर्ग 20-30, l_1=20, i=30-20=10 , f=20, c=3+x
मध्यका (M)=l_1+\frac{1}{f}(m-c) \\ 27=20+\frac{10}{20}\left(\frac{35+x+y}{2}-3-x\right) \\ \Rightarrow 27-20=\frac{1}{2}\left(\frac{35+8+y-6-2 x}{2}\right) \\ \Rightarrow 7 \times 4=37+y-2 \times 8 \\ \Rightarrow y=28-21 \Rightarrow y=7
x=8,y=7 अतः N=50,F(10-20)=8,F(40-50)=7
Example:92.निम्नलिखित अपूर्ण आवृत्ति वितरण प्रस्तुत है।यह ज्ञात है कि कुल आवृत्तियाँ 1000 तथा मध्यका 213.11 है।अज्ञात आवृत्तियाँ ज्ञात कर बहुलक का मान ज्ञात कीजिए:
(The following incomplete frequency distribution is given.It is known that the total of frequencies is 1000 and the median is 213.11.Find out the missing frequencies and then calculate mode):

Solution:माना कि वर्गान्तर 175-200 की आवृत्ति तथा 225-250 की आवृत्ति है।अज्ञात आवृत्तियों को छोड़कर शेष आवृत्तियों का योग =5+17+80+326+88+9=525
जबकि आवृत्तियों का योग 1000 है अतः f_1+f_2=1000-525 \\ \Rightarrow f_1+f_2=475 \cdots(1) \\ m=\frac{N}{2}=\frac{1000}{2}=500
मध्यका 213.11 है अतः मध्यका वर्ग 200-225 है।
l_1=200, i=225-200=25, f=326 ,\\ C=5+17+80+f_1=102+f_1
मध्यका (M)=l_1+\frac{i}{f}(m-c) \\ \Rightarrow 213.11=200+\frac{25}{326}\left(500-102-f_1\right) \\ \Rightarrow 213.11 \times 200=\frac{25}{326}\left(398-f_1\right) \\ \Rightarrow 13.11 \times 326=9950-25 f_1 \\ \Rightarrow 25 f_1=9950-4273.86 \\ =5676.14 \\ \Rightarrow f_1=\frac{5676.14}{25}=227.0456 \\ \Rightarrow f_1=227
समीकरण (1) से:
f_1+f_2=475 \\ 227+f_2=475 \\ \Rightarrow f_2=475-227 \\ \Rightarrow f_2=248 \\ f_1=227, f_2=248
बहुलक (Mode):निरीक्षण द्वारा सबसे अधिक बारम्बारता 326 है अतः बहुलक वर्ग 200-225 है।
l_1=200, i=225-200=25 \\ f_0=227, f_1=326, f_2=240 \\ \Delta_1=f_1-f_0=326-227=99 \\ \Delta_2=f_1-f_2=326-248=78
बहुलक (Z)=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i \\ =200+\frac{99}{99+78} \times 25 \\ =200+\frac{2475}{177} \\=200+13.9830 \\ =213.9830 \\ \Rightarrow Z \approx 213.98
समूहीकरण द्वारा
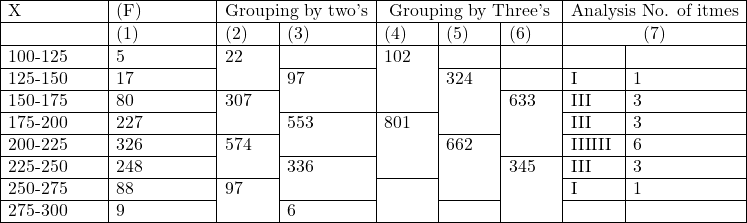
उपर्युक्त विश्लेषण से स्पष्ट है कि 200-225 वर्ग 6 बार (सबसे अधिक बार) आवृत्त होता है जो बहुलक वर्ग है।अतः निरीक्षण तथा समूहीकरण दोनों से बहुलक समान है।
Z \approx 213.98
उपर्युक्त उदाहरणों के द्वारा मध्यका और सरल समान्तर माध्य (Median and Simple Arithmetic Mean),अज्ञात मूल्य अथवा आवृत्ति का निर्धारण (Determination of Unknown Value or Frequency) को समझ सकते हैं।
3.मध्यका और सरल समान्तर माध्य पर आधारित सवाल (Questions Based on Median and Simple Arithmetic Mean):
(1.)निम्न आवृत्ति बंटन में यदि समान्तर माध्य (arithmetic mean) का मान 18 हो तो अज्ञात आवृत्ति (missing frequency) ज्ञात कीजिए।
\begin{array}{|c|c|} \hline \text{वर्गान्तर} & \text{आवृत्ति} \\ \hline 11-13 & 3 \\ \hline 13-15 & 6 \\ \hline 15-17 & 9 \\ \hline 17-19 & 13 \\ \hline 19-21 & ? \\ \hline 21-23 & 5 \\ \hline 23-25 & 4 \\ \hline \end{array}
(2.)अग्रलिखित आवृत्ति बंटन से आकलन रीति द्वारा समान्तर माध्य ज्ञात कीजिए।
\begin{array}{|c|c|} \hline \text{ऊँचाई (फीट में)} & \text{आवृत्ति} \\ \hline 0-7 & 26 \\ \hline 7-14 & 31 \\ \hline 14-21 & 35 \\ \hline 21-28 & 42 \\ \hline 28-35 & 82 \\ \hline 35-42 & 71 \\ \hline 42-49 & 54 \\ \hline 49-56 & 19 \\ \hline \end{array}
उत्तर (Answers):(1.)8 (2.) \overline{x}=30.8 \mathrm{ft} \approx 30 \mathrm{ft} 1 \text {inch }
उपर्युक्त सवालों को हल करने पर मध्यका और सरल समान्तर माध्य (Median and Simple Arithmetic Mean),अज्ञात मूल्य अथवा आवृत्ति का निर्धारण (Determination of Unknown Value or Frequency) को ठीक से समझ सकते हैं।
Also Read This Article:- Simple Arithmetic Mean and Quartile
4.मध्यका और सरल समान्तर माध्य (Frequently Asked Questions Related to Median and Simple Arithmetic Mean),अज्ञात मूल्य अथवा आवृत्ति का निर्धारण (Determination of Unknown Value or Frequency) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.अज्ञात आवृत्तियाँ कैसे ज्ञात करते हैं? (How to Find Unknown Frequencies?):
उत्तर:यदि किसी प्रश्न में किसी मूल्य की आवृत्ति ज्ञात न हो,किन्तु श्रेणी का समान्तर माध्य,मध्यका तथा बहुलक दे रखें हों तो इनके प्रत्यक्ष सूत्र का प्रयोग करके सरल समीकरण उपलब्ध कर लिया जाता है।इन समीकरणों के आधार पर अज्ञात आवृत्तियाँ ज्ञात की जा सकती है।
प्रश्न:2.बहुलक की गणना कैसे करते हैं? (How to Calculate Mode?):
उत्तर:(1.) व्यक्तिगत श्रेणी में निरीक्षण द्वारा इसका निर्धारण करेंगे अथवा इन्हें पहले खण्डित चर में परिवर्तित कर बहुलक का निर्धारण कर लेंगे।
(2.)समावेशी सतत चर है तो उसे अपवर्जी चर में परिवर्तित करना आवश्यक है।
(3.)सभी वर्गों के अन्तर समान होने चाहिए।यदि असमान है तो उन्हें संशोधन कर समान बना लें।यदि वर्गों को समान बनाना सम्भव ही नहीं है तो या तो असमान वर्गों के आधार पर ही बहुलक का निर्धारण कर लें अथवा निम्न सूत्र द्वारा बहुलक ज्ञात करेंः
Z=3 M-2 \overline{X}
(4.)बहुलक वर्ग ज्ञात कर इसी सूत्र का प्रयोग करें
Z=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i (ऋणात्मक चिन्ह छोड़कर)
प्रश्न:3.कारण सहित बतलाइए कि कक्षा में विद्यार्थियों का बौद्धिक स्तर में कौनसा समान्तर माध्य ज्ञात करना उपयुक्त होगा? (Explain with Reason Which of the Average Will be Suitable in Average Level of Intelligence of Students in a Class?):
उत्तर:विद्यार्थियों का बौद्धिक स्तर ज्ञात करने हेतु कक्षा में विद्यार्थियों के माध्य स्तर की गणना करनी होगी।चूंकि यह गुणात्मक तथ्य है,अतः मध्यका (median) ही सर्वाधिक उपयुक्त माध्य होगा।
उपर्युक्त प्रश्नों के उत्तर द्वारा मध्यका और सरल समान्तर माध्य (Median and Simple Arithmetic Mean),अज्ञात मूल्य अथवा आवृत्ति का निर्धारण (Determination of Unknown Value or Frequency) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Median and Simple Arithmetic Mean
मध्यका और सरल समान्तर माध्य
(Median and Simple Arithmetic Mean)
Median and Simple Arithmetic Mean
मध्यका और सरल समान्तर माध्य (Median and Simple Arithmetic Mean) के इस आर्टिकल में
मध्यका,समान्तर माध्य और अज्ञात मूल्य अथवा अज्ञात आवृत्ति ज्ञात करके सवालों को समझने
का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.








