Surface Area and Volume of Cylinder
1.बेलन का पृष्ठीय क्षेत्रफल एवं आयतन (Surface Area and Volume of Cylinder):
बेलन का पृष्ठीय क्षेत्रफल एवं आयतन (Surface Area and Volume of Cylinder):मापन जार,गोल खम्भे,गोल पाइप,टेस्ट ट्यूब इत्यादि ऐसी वस्तुएं हैं जिसमें एक पार्श्व वक्र पृष्ठ (Lateral Curved Surface) और सर्वांगसम वृत्तीय अनुप्रस्थ काट (Cross Section) हो, वृत्तीय बेलन (Circular Cylinder) कहलाता है।वृत्तीय अनुप्रस्थ काटों के केंद्रों को मिलाने वाली रेखा को बेलन का अक्ष कहते हैं।यदि बेलन का अक्ष वृत्तीय अनुप्रस्थ काट पर लम्ब है,तो उस बेलन को लम्बवृत्तीय बेलन (Right Circular Cylinder) कहते हैं।
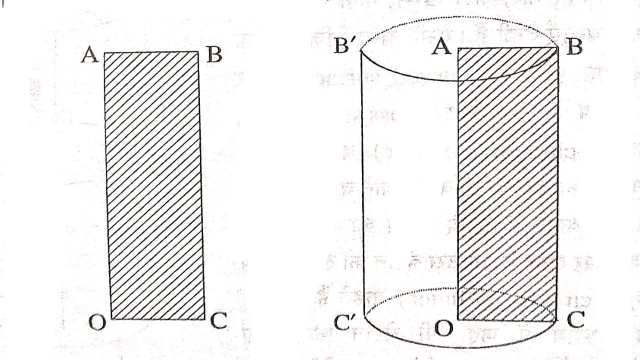
एक उर्ध्वाधर रेखाखण्ड OA लीजिए।इसके समान एक अन्य रेखाखंड CB इस प्रकार लीजिए कि बिंदुओं O,A,B,C से मिलाने पर एक आयत बनता है।माना कि रेखाखण्ड CB रेखाखण्ड OA के चारों ओर एक चक्कर लगाकर पुनः अपनी प्रारंभिक स्थिति में आ जावे।इस परिक्रमण से त्रिज्या AB और ऊंचाई OA का एक बेलनीय पृष्ठ जनित होता है,जो खोखला और दोनों सिरों से खुला है।
यदि रेखाखंड ABCD एक आयताकार क्षेत्र है,यह रेखाखण्ड OA के चारों ओर परिक्रमा करता है तो हमें AB त्रिज्या का तथा OA ऊंचाई का ठोस बेलन प्राप्त होता है।यह आकृति में दर्शाया गया है।
वे रेखाएं जो OA के समांतर है और बेलन के पार्श्व पृष्ठ पर स्थित हैं जनक (Generates ) कहलाती हैं।यहाँ रेखाएं BC,B’C’ जनक है।बेलन को उर्ध्वाधर स्थिति में रखने पर नीचे के वृत्तीय सिरे को बेलन का आधार कहते हैं।रेखाखण्ड CB की लम्बाई, बेलन की ऊँचाई कही जाती है।वृत्तीय सिरे की त्रिज्या को बेलन की त्रिज्या कहते हैं।
खोखले बेलन में दोनों सिरे खुले होते हैं।ठोस बेलन में दोनों सिरे बंद होते हैं।r त्रिज्या और h ऊंचाई वाला बेलन का वक्र पृष्ठ ज्ञात करने के लिए माना कि बेलन खोखला है कागज (अथवा धातु ) की बारीक चद्दर से बना है।
यदि वक्रपृष्ठ को रेखाखंड BC के अनुदिश काटकर खोल दिया जाए तो यह आयत BCDE के रूप का हो जाएगा।
जब चद्दर बेलन के वक्र पृष्ठ के रूप में है तो रेखाखंड BC तथा ED संपाती है।
अतः की BC की लंबाई=h बेलन की ऊंचाई
CD की लंबाई=बेलन के की परिधि जिसकी त्रिज्या है आयत का क्षेत्रफल बेलन के एक सिरे की परिधि जिसकी त्रिज्या r है
CD=2 \pi r
(1.)अत: बेलन के वक्रपृष्ठ का क्षेत्रफल (Curved Surface Area of the Cylinder)=आयत BCDE का क्षेत्रफल
=2 \pi r \times h \\ =2 \pi r h
(2.)बेलन के आधार का क्षेत्रफल (Area of the Base of the Cylinder)=\pi r^{2}
(3.)बेलन के संपूर्ण पृष्ठ का क्षेत्रफल (Total Surface Area of the Cylinder)=वक्र पृष्ठ का क्षेत्रफल+2 × आधार का क्षेत्रफल
=2 \pi r h+2 \pi r^{2} \\ =2 \pi r(h+r)
(4.)बेलन द्वारा घेरा गया स्थान उसका आयतन होता है। यदि बेलन की त्रिज्या r और ऊंचाई h है तो बेलन का आयतन (Volume of Cylinder)= आधार का क्षेत्रफल × ऊंचाई
=\pi r^{2} \times h \\ =\pi r^{2} h
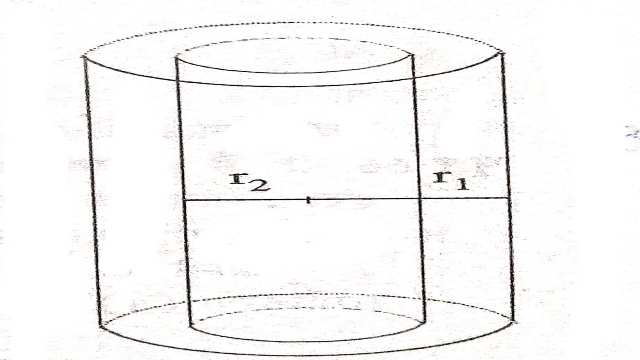
(5.)यदि एक खोखले बेलन की बाह्य त्रिज्या r_{1} तथा अन्त: त्रिज्या r_{2} है तथा उसकी ऊंचाई h है तो
खोखले बेलन का आयतन (Volume of Hollow Cylinder)=\pi r_{1}^{2} h-\pi r_{2}^{2} h \\ =\pi (r_{1}^{2} -r_{2}^{2}) h
खोखले बेलन का संपूर्ण पृष्ठीय क्षेत्रफल (Total Surface Area of Hollow Cylinder)=2 \pi r_{1} h+2 \pi r_{2} h+2 \pi r_{1}^{2}-2 \pi r_{2}^{2} \\ =2 \pi h(r_{1}+r_{2} )+2 \pi (r_{1}^{2} -r_{2}^{2}) \\ =2 \pi h(r_{1}+r_{2} )+2 \pi h(r_{1}+r_{2} )(r_{1}-r_{2} ) \\ =2 \pi h(r_{1}+r_{2} )(h+r_{1}-r_{2} )
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Surface Area and Volume of Cuboid
2.बेलन का पृष्ठीय क्षेत्रफल एवं आयतन के उदाहरण (Surface Area and Volume of Cylinder Examples):
Example:1.एक बेलन का व्यास 14 सेमी और ऊंचाई 15 सेमी है।बेलन का संपूर्ण पृष्ठीय क्षेत्रफल और आयतन ज्ञात कीजिए।
Solution:बेलन का व्यास=14 सेमी
त्रिज्या (r)= \frac{14}{2} सेमी=7 सेमी
ऊँचाई (h)=15 सेमी,
बेलन का संपूर्ण पृष्ठीय क्षेत्रफल=2 \pi r(h+r) \\ =2 \times \frac{22}{7} \times 7 \times (15+7) \\ 44 \times 22 \\ 968 वर्ग सेमी
बेलन का आयतन=\pi r^{2} h \\ =\frac{22}{7} \times 7^{2} \times 15 \\=2310
Example:2. एक लंबवृत्तीय बेलन की ऊंचाई 7सेमी और आधार की त्रिज्या 3 सेमी है।इसका वक्रपृष्ठीय क्षेत्रफल,संपूर्ण पृष्ठीय क्षेत्रफल और आयतन ज्ञात कीजिए।
Solution: बेलन की ऊंचाई (h)= 7 सेमी
बेलन की त्रिज्या (r)=3 सेमी
बेलन का वक्र पृष्ठीय क्षेत्रफल=2 \pi r h \\ 2 \times \frac{22}{7} \times 3 \times 7 \\ =132 वर्ग सेमी
बेलन का संपूर्ण पृष्ठ क्षेत्रफल=2 \pi r(h+r) \\ =2 \times \frac{22}{7} \times 3 \times (7+3) \\ =\frac{2 \times 22 \times 3 \times 10}{7} \\ =188.57 वर्ग सेमी
बेलन का आयतन=\pi r^{2} h \\ =\frac{22}{7} \times 3^{2} \times 7 \\=198 घन सेमी
Example:3.एक बेलन के सिरे का क्षेत्रफल 154 वर्ग सेमी है तथा इसकी ऊंचाई 21 सेमी है।बेलन का आयतन एवं वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
Solution:बेलन के सिरे का क्षेत्रफल=वृत्त का क्षेत्रफल
\pi r^{2}=154 \\ \Rightarrow \frac{22}{7} \times r^{2}=154 \\ \Rightarrow r^{2}=\frac{154 \times 7}{22} \\ \Rightarrow r^{2}=7^{2} \\ \Rightarrow r=7 सेमी
बेलन का आयतन=एक सिरे का क्षेत्रफल × ऊँचाई=\pi r^{2} h \\ 154 \times 21 \\ =3234
बेलन का वक्र पृष्ठ का क्षेत्रफल=2 \pi r h \\ =2 \times \frac{22}{7} \times 7 \times 21 \\ =44 \times 21 \\ =924 वर्ग सेमी
Example:4.दो लम्बवृत्तीय की त्रिज्याओं का अनुपात 2:3 तथा ऊंचाइयों का अनुपात 5:4 है तो दोनों बेलनों के वक्र पृष्ठीय क्षेत्रफलों तथा आयतनों का अनुपात ज्ञात कीजिए।
Solution: माना पहले बेलन की त्रिज्या r_{1} तथा ऊंचाई h_{1} है।
तथा दूसरे बेलन की त्रिज्या r_{2} तथा ऊंचाई h_{2} है।
अतः \frac{r_{1}}{r_{2}}=\frac{2}{3} तथा \frac{h_{1}}{h_{2}}=\frac{5}{4}
वक्र पृष्ठीय क्षेत्रफलों का अनुपात=\frac{2 \pi r_{1} h_{1}}{2 \pi r_{2} h_{2}} \\ =\frac{r_{1}}{r_{2}} \times \frac{h_{1}}{h_{2}} \\ = \frac{2}{3} \times \frac{5}{4}=\frac{5}{6}
अतः वक्र पृष्ठीय क्षेत्रफलों का अनुपात=5:6 है।
आयतनों का अनुपात=\frac{\pi r_{1}^{2} h_{1}}{\pi r_{2}^{2} h_{2}} \\ =\left(\frac{r_{1}}{r_{2}}\right)^{2} \times \left(\frac{h_{1}}{h_{2}}\right) \\ =\left(\frac{2}{3}\right)^{2} \times \frac{5}{4} \\ =\frac{4}{9} \times \frac{5}{4}=\frac{5}{9}
अतः आयतनों का अनुपात 5:9 है।
Example:5.एक ठोस बेलन का संपूर्ण पृष्ठीय क्षेत्रफल 462 वर्ग सेमी है।इसका वक्र पृष्ठीय क्षेत्रफल,संपूर्ण पृष्ठीय क्षेत्रफल का एक तिहाई है।बेलन का आयतन ज्ञात कीजिए।
Solution:बेलन का संपूर्ण पृष्ठीय क्षेत्रफल 462 वर्ग सेमी
वक्र पृष्ठीय क्षेत्रफल =\frac{\text {सम्पूर्ण पृष्ठीय क्षेत्रफल}}{3} \\ \frac{462}{3}=154 वर्ग सेमी
अतः 2 \pi r h=154
तथा 2 \pi r(h+r)=462 \\ \Rightarrow 2 \pi r h+2 \pi r^{2}=462 \\ \Rightarrow 154+2 \pi r^{2}=462 \\ \Rightarrow 2 \pi r^{2}=462-154 \\ \Rightarrow 2 \times \frac{22}{7} \times r^{2}=308 \\ r^{2}=\frac{308 \times 7}{22 \times 2}=49 \\ r=\sqrt{49}=7 सेमी
2 \pi r h=154 \\ 2 \times \frac{22}{7} \times r \times h=154 \\ 2 \times \frac{22}{7} \times 7 \times h=154 \\ h=\frac{154}{44}=\frac{7}{2} सेमी
बेलन का आयतन=\pi r^{2} h= \frac{22}{7} \times 7 \times 7 \times \frac{7}{2}=539 घनसेमी
Example:6.एक बेलन का वक्र पृष्ठीय क्षेत्रफल 660 वर्ग सेमी है तथा ऊँचाई 15 सेमी है।इसका आयतन ज्ञात कीजिए।
Solution:बेलन का का वक्र पृष्ठीय क्षेत्रफल=2 \pi r h \\ 2 \pi r h=660 \text { वर्ग सेमी } \\ \Rightarrow 2 \times \frac{22}{7} \times 72 \times 15=660[\because h=15 \text { सेमी } ]\\ \Rightarrow r=\frac{660 \times 7}{2 \times 22 \times 15}=7 \text { सेमी }
बेलन का आयतन=\pi r^{2} h \\ =\frac{22}{7} \times(7)^{2} \times 15 \\ =2310 घन सेमी
Example:7.एक बेलन का आयतन 30 \pi \text{ सेमी }^{3} है तथा आधार का क्षेत्रफल 6 \pi \text{ सेमी }^{2} है।बेलन की ऊंचाई ज्ञात कीजिए।
Solution:बेलन के आधार का क्षेत्रफल (वृत्त)=\pi r^{2} \\ \pi r^{2}=6 \pi \\ \Rightarrow r^{2}=6
बेलन का आयतन=\pi r^{2} h \\ \pi r^{2} h=30 \pi \\ \Rightarrow \pi \times 6 \times h=30 \pi \\ \Rightarrow h=\frac{30 \pi}{6 \pi} \\ \Rightarrow h=5 सेमी
Example:8.एक बेलन का आयतन और वक्र पृष्ठीय क्षेत्रफल क्रमशः1650 घन सेमी और 660 वर्ग सेमी है। बेलन की त्रिज्या और ऊंचाई ज्ञात कीजिए।
Solution:बेलन का आयतन=\pi r^{2} h \\ \pi r^{2} h=1650 \cdots(1)
बेलन का वक्र पृष्ठीय क्षेत्रफल=2 \pi r h \\ 2 \pi r h=660 \cdots (2)
समीकरण (1) में (2) का भाग देने पर:
\frac{\pi r^{2} h}{2 \pi r h}=\frac{1650}{660} \\ \Rightarrow r=\frac{1650 \times 2}{660}=5 सेमी
समीकरण से (2) से:
2 \pi r h=660 \\ 2 \times \frac{22}{7} \times 5 \times h=660 \\ \Rightarrow h=\frac{660 \times 7}{2 \times 22 \times 5} \\ \Rightarrow h=21
Example:9.एक बेलन की ऊंचाई व त्रिज्या क्रमशः 7.5 सेमी और 3.5 सेमी है।इसके संपूर्ण पृष्ठीय क्षेत्रफल और वक्र पृष्ठीय क्षेत्रफल में अनुपात ज्ञात कीजिए।
Solution:ऊँचाई (h)=7.5 सेमी
त्रिज्या (r)=3.5 सेमी
\frac{ \text{ सम्पूर्ण पृष्ठ का क्षेत्रफल}}{\text{ वक्र पृष्ठ का क्षेत्रफल }}=\frac{ 2 \pi r (h+r)}{2 \pi r h} \\ =\frac{r+h}{h} \\ =\frac{3.5+7.5}{7.5} \\ =\frac{11}{7.5}=\frac{110}{75} \\ =\frac{22}{15}
अतः सम्पूर्ण पृष्ठीय क्षेत्रफल और वक्र पृष्ठीय क्षेत्रफल में अनुपात=22:15 है।
Example:10.20 मीटर गहरा और 7 मीटर व्यास का एक कुआं खोदा गया।इससे निकली मिट्टी से 22 मीटर ×14 मीटर माप का एक चबूतरा बनाया गया।चबूतरे की ऊंचाई ज्ञात कीजिए।
Solution:कुएं की गहराई (h)=20 मीटर
कुएं की त्रिज्या (r)=\frac{7}{2} मीटर
चबूतरे (घनाभ) की लंबाई=20 मीटर
चबूतरे की चौड़ाई=14 मीटर
चबूतरे की ऊंचाई=H (माना)
अतः कुएं से निकली मिट्टी का आयतन (बेलन)=चबूतरे का आयतन (घनाभ)
\pi r^{2} h=l \times b \times H \\ \Rightarrow \frac{22}{7} \times\left(\frac{7}{2}\right)^{2} \times 20=20 \times 14 \times H \\ \Rightarrow H=\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 20 \times \frac{1}{20} \times \frac{1}{14} \\ \Rightarrow H=2.75 मीटर
Example:11.एक बेलनाकार बर्तन में 30800 घन सेमी पानी भरा जा सकता है।यदि बर्तन की भीतरी त्रिज्या 14 सेमी है तो उसका भीतरी वक्र पृष्ठ ज्ञात कीजिए।
Solution:बेलन का आयतन=\pi r^{2} h=30800 घन सेमी
\Rightarrow \frac{22}{7} \times 14 \times 14 \times h=30800[r=14] \\ \Rightarrow h=\frac{30800 \times 7}{22 \times 14 \times 14} \\ \Rightarrow h=50 सेमी
भीतरी वक्र पृष्ठ का क्षेत्रफल=2 \pi r h \\ =2 \times \frac{22}{7} \times 14 \times 50 \\ =4400 वर्ग सेमी
Example:12.एक खोखले बेलन की मोटाई 2 सेमी है।इसका भीतरी व्यास 14 सेमी है तथा ऊंचाई 26 सेमी है।बेलन के दोनों सिरे खुले हुए हैं।खोखले बेलन का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
Solution:भीतरी व्यास=14 सेमी
भीतरी त्रिज्या (r_{2})=\frac{14}{2}=7 सेमी
मोटाई =2 सेमी
बाहरी त्रिज्या (r_{1})=7+2=9 सेमी
ऊँचाई (h)=26 सेमी
संपूर्ण पृष्ठीय क्षेत्रफल=2 \pi\left(r_{1}+r_{2}\right)\left(h+r_{1}-r_{2}\right) \\ =2 \times \frac{22}{7} \times(9+7)(26+9-7) \\ =2 \times \frac{22}{7} \times 16 \times 28=2816 वर्ग सेमी
Example:13.एक खोखला बेलन दोनों सिरों से खुला हुआ है।उसकी ऊंचाई 20 सेमी तथा अंत: एवं बाह्य व्यास क्रमशः 26 सेमी तथा 30 सेमी है।इस खोखले बेलन का आयतन ज्ञात कीजिए।
Solution:बाह्य व्यास=30 सेमी
बाह्य त्रिज्या (r_{1})=\frac{30}{2}=15 सेमी
अन्त:व्यास =26 सेमी
अन्त:त्रिज्या (r_{2})=\frac{26}{2}=13 सेमी
खोखले बेलन का आयतन=\pi r_{1}^{2} h-\pi r_{2}^{2} h\\ =\pi\left(r_{1}^{2}-r_{2}^{2}\right) h \\ = \pi \left(r_{1}+r_{2} \right) \left(r_{1}-r_{2}\right) h\\ =\frac{22}{7} \times(15+13) \cdot(15-13) \times 20 \\ =\frac{22}{7} \times 28 \times 2 \times 20 \\ =3520 घन सेमी
उपर्युक्त उदाहरणों के द्वारा बेलन का पृष्ठीय क्षेत्रफल एवं आयतन (Surface Area and Volume of Cylinder) को समझ सकते हैं।
3.बेलन का पृष्ठीय क्षेत्रफल एवं आयतन की समस्याएं (Surface Area and Volume of Cylinder Problems):
(1.)यदि एक बेलन का व्यास 14 सेमी और ऊंचाई 15 सेमी है तो उसका संपूर्ण पृष्ठ और आयतन ज्ञात कीजिए।
(लीजिए \pi =\frac{22}{7})
(2.)एक बेलन की ऊँचाई 11 सेमी है तथा उसका वक्र पृष्ठीय क्षेत्रफल 968 वर्गसेमी है।बेलन की त्रिज्या ज्ञात कीजिए।
(लीजिए \pi =\frac{22}{7})
(3.)बेलनाकार एक खंभे का आयतन 115.5 घन मीटर है तथा उसका वक्र पृष्ठ 66 वर्ग मीटर है।खंभे की ऊंचाई ज्ञात कीजिए।
(लीजिए \pi =\frac{22}{7})
(4.)एक बेलन की त्रिज्या और ऊंचाई का अनुपात 1:3 है। यदि बेलन का आयतन 3234 घन सेमी हो तो बेलन का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
उत्तर (Answers):(1.)संपूर्ण पृष्ठीय क्षेत्रफल=968 वर्ग सेमी,आयतन=2310 घन सेमी
(2.)r=14 सेमी
(3.)h=3 मीटर
(4.)संपूर्ण पृष्ठीय क्षेत्रफल=1232 वर्गसेमी
उपर्युक्त सवालों को हल करने पर बेलन का पृष्ठीय क्षेत्रफल एवं आयतन (Surface Area and Volume of Cylinder) को ठीक से समझ सकते हैं।
Also Read This Article:-Properties of Circle
4.बेलन का पृष्ठीय क्षेत्रफल एवं आयतन (Surface Area and Volume of Cylinder) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.क्या बेलन का आयतन पृष्ठीय क्षेत्रफल से अधिक होता है? (Is the volume of a cylinder greater than the surface area?):
उत्तर:पृष्ठीय क्षेत्रफल कभी भी किसी भी आकृति के आयतन से बड़ा नहीं हो सकता।न तो आयतन कभी भी पृष्ठीय क्षेत्रफल से अधिक हो सकता है।
यदि एक ही आकृति का पृष्ठीय क्षेत्रफल तथा आयतन ज्ञात किया जाए तथा एक ही इकाई हो तो हमेशा आयतन अधिक होता है।
प्रश्न:2.सिलेंडर का सूत्र क्या होता है? (What is a formula of cylinder?):
उत्तर:बेलन के आयतन का सूत्र (The formula for the volume of a cylinder) V=Bh या V=πr^2h है।बेलन की त्रिज्या 8 सेमी और ऊंचाई 15 सेमी है।सूत्र V=πr^2h में r के लिए 8 और h के लिए 15 प्रतिस्थापित करें।अत: बेलन का आयतन लगभग 3016 घन सेंटीमीटर है।
प्रश्न:3.क्या पृष्ठीय क्षेत्रफल आयतन से छोटा है? (Is surface area smaller than volume?):
उत्तर:पृष्ठीय क्षेत्रफल तथा आयतन की तुलना नहीं की जा सकती है।परन्तु यदि संख्यात्मक मान की तुलना की जाए तो पृष्ठीय क्षेत्रफल आयतन से बड़ा और आयतन से कम होता है,यह इस बात पर निर्भर करता है कि हम किन इकाइयों का उपयोग करते हैं।
प्रश्न:4.पृष्ठीय क्षेत्रफल और आयतन के बीच क्या संबंध है? (What is the relationship between surface area and volume?):
आयतन में वृद्धि हमेशा पृष्ठीय क्षेत्रफल में वृद्धि से अधिक होती है।यह घन,गोले या किसी अन्य वस्तु के लिए सही है जिसका आकार (shape) बदले बिना उसकी माप (size) बढ़ा दिया जाता है।
प्रश्न:5.हम पृष्ठीय क्षेत्रफल की गणना क्यों करते हैं? (Why do we calculate surface area?):
उत्तर:रासायनिक गतिकी (chemical kinetics) में पृष्ठीय क्षेत्रफल महत्वपूर्ण है।किसी पदार्थ (substance) का पृष्ठीय क्षेत्रफल बढ़ने से सामान्यतः रासायनिक अभिक्रिया की दर (rate of a chemical reaction) बढ़ जाती है।उदाहरण के लिए,एक महीन पाउडर (fine powder) में लोहा दहन (combust) करेगा,जबकि ठोस ब्लॉकों (solid blocks) में यह संरचनाओं में उपयोग करने के लिए पर्याप्त स्थिर (stable enough) है।
प्रश्न:6.सिलेंडर के गुण क्या हैं? (What is the properties of cylinder?):
उत्तर:सिलेंडर परिभाषा:एक सिलेंडर एक त्रि-आयामी ठोस होता है जिसमें एक वक्र सतह (curved surface) से जुड़े दो समानांतर आधार होते हैं।आधार आमतौर पर आकार में वृत्ताकार होते हैं।आधारों के बीच की लम्बवत दूरी को बेलन की ऊँचाई “h” के रूप में दर्शाया जाता है और “r” बेलन की त्रिज्या है।
प्रश्न:7.सिलेंडर का किनारा क्या है? (What is edge of cylinder?):
उत्तर:एक बेलन एक वृत्ताकार समतल सतह पर खड़ा होता है जिसके ऊपर और नीचे वृत्ताकार समतल पृष्ठ होते हैं।इसके दो किनारे होते हैं,जिस पर दो समतल सतह वक्र सतह से मिलती हैं।ये किनारे वक्र किनारे हैं (curved edges)।एक बेलन में 2 समतल पृष्ठ और 1 वक्र पृष्ठ होते हैं।2 किनारे (edges) हैं और कोई कोने (vertices) नहीं हैं।
प्रश्न:8.बेलन के आधार का आकार कैसा होता है? (What is the shape of base of cylinder?):
उत्तर:वृत्ताकार
सिलेंडर/आधार आकार
बेलन का आधार क्षेत्रफल वास्तव में एक वृत्त का क्षेत्रफल है क्योंकि बेलन का आधार एक वृत्त है।एक बेलन एक त्रि-आयामी ठोस आकृति है जिसमें एक वक्राकार फलक (curved face) से जुड़े दो वृत्ताकार आधार होते हैं।
प्रश्न:9.क्या आयतन और पृष्ठीय क्षेत्रफल सीधे आनुपातिक हैं? (Are volume and surface area directly proportional?):
उत्तर:सतह/आयतन लंबाई के व्युत्क्रमानुपाती होता है।
इसका मतलब यह है कि एक बड़ी वस्तु की सतह उसके आयतन के सापेक्ष कम होगी,उसी आकार की एक छोटी आइसोमेट्रिक वस्तु (isometric object) की तुलना में।
प्रश्न:10.सतह क्षेत्र और आयतन का आविष्कार किसने किया? (Who invented surface area and volume?):
उत्तर:गणित के इतिहास में एक शानदार मील का पत्थर (spectacular landmark) आर्किमिडीज़ (Archimedes) (287-212 ईसा पूर्व) की खोज थी कि एक ठोस गोले का आयतन उसके चारों ओर के सबसे छोटे बेलन के आयतन का दो-तिहाई होता है और यह कि गोले का पृष्ठीय क्षेत्रफल भी होता है एक ही बेलन के कुल पृष्ठीय क्षेत्रफल का दो-तिहाई।
प्रश्न:11.सिलेंडर के पांच गुण क्या हैं? (What are the five properties of cylinder?):
उत्तर:सिलेंडर
आधार और भुजा।एक सिलेंडर एक ज्यामितीय ठोस है जो रोजमर्रा की जिंदगी में बहुत आम है,जैसे सूप कैन (soup can)।
ऊंचाई।ऊँचाई h आधारों के बीच की लम्बवत दूरी है।
त्रिज्या।एक बेलन की त्रिज्या r एक आधार की त्रिज्या है।
अक्ष (Axis)।प्रत्येक आधार के केंद्र को मिलाने वाली रेखा।
प्रश्न:12.सिलेंडर आकार परिभाषा क्या है? (What is cylinder shape definition?):
उत्तर:एक सिलेंडर एक बेलनाकार आकार और दो समानांतर वृत्ताकार आधारों से घिरा एक ठोस आकार होता है।
प्रश्न:13.लम्ब वृत्तीय बेलन के क्या गुण होते हैं? (What are the properties of right circular cylinder?):
उत्तर:एक लम्ब वृत्तीय बेलन (right circular cylinder) के गुण हैं:
इसमें दो वक्र किनारे (curved edges),एक वक्र सतह (curved surface) और दो सपाट फलक (flat faces) होते हैं।
आधार सदैव एक दूसरे के सर्वांगसम होते हैं।
बेलन का आकार (size) आधार की त्रिज्या और बेलन की ऊंचाई पर निर्भर करता है।
प्रश्न:14.सिलेंडर में कितने किनारे होते हैं? (How many edges are in cylinder?):
उत्तर:ठोस आकृतियाँ किनारों का सामना करती हैं
परिभाषा एक फलक (face) एक ठोस वस्तु की किसी एक सपाट सतह को संदर्भित करता है।एक किनारा सीमा पर एक रेखा खंड (edge is a line segment on the boundary) है जो एक शीर्ष (कोने बिंदु) को दूसरे से जोड़ता है।
Solid Shapes Faces Edges
गोला \quad \quad 1 \quad \quad 0
सिलेंडर \quad 2 \quad \quad 2
शंकु \quad \quad 1 \quad \quad 1
प्रश्न:15.π क्या है? (What is the π?):
उत्तर:संक्षेप में,pi—जिसे ग्रीक अक्षर p या π के रूप में लिखा जाता है जो किसी वृत्त की परिधि और उस वृत्त के व्यास का अनुपात है।वृत्त के आकार के बावजूद,यह अनुपात हमेशा पाई के बराबर होगा।दशमलव रूप में pi का मान लगभग 3.14 होता है।
प्रश्न:16.वॉल्यूम किसने खोजा? (Who Found volume?):
उत्तर:आर्किमिडीज (Archimedes)
आर्किमिडीज (जन्म सी. 287 ईसा पूर्व,सिरैक्यूज़,सिसिली [इटली] [Syracuse, Sicily [Italy]]- 212/211 ईसा पूर्व, सिरैक्यूज़ (Syracuse)),प्राचीन ग्रीस (ancient Greece) में सबसे प्रसिद्ध गणितज्ञ और आविष्कारक।आर्किमिडीज विशेष रूप से एक गोले की सतह और आयतन और उसके परिचालित सिलेंडर के बीच संबंध की खोज के लिए महत्वपूर्ण है।
उपर्युक्त प्रश्नों के उत्तर द्वारा बेलन का पृष्ठीय क्षेत्रफल एवं आयतन (Surface Area and Volume of Cylinder) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा बेलन का पृष्ठीय क्षेत्रफल एवं आयतन (Surface Area and Volume of Cylinder) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |